太阳方位角的计算

计算日出日落的方位角度公式要计算任意一个地方在任意一天日出日落的方位角度，可以用下面的公式：方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]公式中，M表示的是某天太阳直射的纬度，N表示的是某地的纬度，^2表示平方。

例如，北京在北纬40度，则N=40，夏至这一天太阳在北纬23.5度（太阳直射北纬23.5度），即M=23.5，把N和M的值代入上式，可求得方位角=31度意思是，夏至这一天，在北京的人看来，太阳是从东偏北31度的方位升起的，是在西偏北31度的方位落下的。

说明：1本公式是在理想条件下推导出来的，即假设地球是个标准球体。

而实际上地球两极略扁，而且各地也有高山、洼地等，所以计算结果可能与实测结果有一点误差。

2 太阳围绕地球旋转的轨迹实际上是螺旋线（好象在地球外面套一根弹簧），所以实际上每天日出和日落的方位角稍微有点差别。

例如，在春分到夏至这段时间，日出方位角要略小于日落方位角。

昼夜长短的计算公式：Cost=-tgδ*tgφ太阳视位置太阳视位置指从地面上看到的太阳的位置，用太阳高度角和太阳方位角两个角度作为坐标表示。

太阳高度角指从太阳中心直射到当地的光线与当地水平面的夹角，其值在0°到90°之间变化，日出日落时为零，太阳在正天顶上为90°（本万年历中显示的高度角均已进行了蒙气差的订正，蒙气差值取自天文年历）。

太阳方位角即太阳所在的方位，指太阳光线在地平面上的投影与当地子午线的夹角，可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。

方位角以正南方向为零，由南向东向北为负，由南向西向北为正，如太阳在正东方，方位角为-90°，在正东北方时，方位为-135°，在正西方时方位角为90°，在正北方时为±180°。

实际上太阳并不总是东升西落，只有在春秋分两天，太阳是从正东方升，正西方落。

在北半球，从春分到秋分的夏半年中，太阳从东偏北的方向升（方位角为-90°到-180°之间），在西偏北的方向落（方位角为90°到180°之间）；而从秋分到下一年春分的冬半年中，太阳从东偏南的方向升（方位角为-90°到0°之间），在西偏南的方向落（方位角为0°到90°之间）。

计算日出日落的方位角度公式要计算任意一个地方在任意一天日出日落的方位角度，可以用下面的公式：方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]公式中，M表示的是某天太阳直射的纬度，N表示的是某地的纬度，^2表示平方。

例如，北京在北纬40度，则N=40，夏至这一天太阳在北纬23.5度（太阳直射北纬23.5度），即M=23.5，把N和M的值代入上式，可求得方位角=31度意思是，夏至这一天，在北京的人看来，太阳是从东偏北31度的方位升起的，是在西偏北31度的方位落下的。

说明：1本公式是在理想条件下推导出来的，即假设地球是个标准球体。

而实际上地球两极略扁，而且各地也有高山、洼地等，所以计算结果可能与实测结果有一点误差。

2 太阳围绕地球旋转的轨迹实际上是螺旋线（好象在地球外面套一根弹簧），所以实际上每天日出和日落的方位角稍微有点差别。

例如，在春分到夏至这段时间，日出方位角要略小于日落方位角。

昼夜长短的计算公式：Cost=-tgδ*tgφ太阳视位置太阳视位置指从地面上看到的太阳的位置，用太阳高度角和太阳方位角两个角度作为坐标表示。

太阳高度角指从太阳中心直射到当地的光线与当地水平面的夹角，其值在0°到90°之间变化，日出日落时为零，太阳在正天顶上为90°（本万年历中显示的高度角均已进行了蒙气差的订正，蒙气差值取自天文年历）。

太阳方位角即太阳所在的方位，指太阳光线在地平面上的投影与当地子午线的夹角，可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。

方位角以正南方向为零，由南向东向北为负，由南向西向北为正，如太阳在正东方，方位角为-90°，在正东北方时，方位为-135°，在正西方时方位角为90°，在正北方时为±180°。

实际上太阳并不总是东升西落，只有在春秋分两天，太阳是从正东方升，正西方落。

在北半球，从春分到秋分的夏半年中，太阳从东偏北的方向升（方位角为-90°到-180°之间），在西偏北的方向落（方位角为90°到180°之间）；而从秋分到下一年春分的冬半年中，太阳从东偏南的方向升（方位角为-90°到0°之间），在西偏南的方向落（方位角为0°到90°之间）。

arcgis 太阳辐射计算公式
ArcGIS软件中太阳辐射计算通常涉及到太阳高度角和太阳方位角的计算。

太阳高度角是指太阳在天空中的位置，而太阳方位角则是指太阳在地平面上的位置。

这两个参数可以用来估算太阳辐射的强度。

太阳高度角的计算公式可以用如下的方式表示：
sin(δ) = sin(φ) sin(θ) + cos(φ) cos(θ) cos(H)。

其中，δ表示太阳高度角，φ表示观测点的纬度，θ表示太阳赤纬，H表示太阳时角。

太阳方位角的计算公式可以用如下的方式表示：
cos(α) = (sin(δ) sin(φ) sin(θ)) / (cos(δ)
cos(φ))。

其中，α表示太阳方位角。

在ArcGIS中，可以通过使用内置的工具或者编写自定义的脚本来实现太阳辐射的计算。

一般来说，这些计算公式会结合地理空间数据，比如地形、太阳轨迹等信息，来进行太阳辐射的空间分布模拟和分析。

总的来说，太阳辐射计算涉及到复杂的天文和地理信息计算，需要综合考虑地球的自转、公转、赤道倾斜等因素，而ArcGIS作为专业的地理信息系统软件，提供了丰富的工具和功能来进行太阳辐射计算和分析。

希望这个回答能够帮助到你。

最近为了更精确地计算楼房的采光情况特意推导了一下太阳高度角和方位角的计算式，现在将得到的几个相关公式贴出来，希望对需要的人有所帮助。

（1）太阳直射点纬度的公式：太阳直射点的纬度为β（北纬β取正值，南纬β取负值），黄道面与赤道面的二面角为α（α即地理和天文中的“黄赤交角”，α的大小为23.5°），太阳在黄道上的点相对春分点的角度为ω（ω以下简称“黄道角”，一年中某天的ω角度可利用这天与春分日3月21日的天数差 n 表示，对平年近似算式为ω = 360°* n / 365 ，对闰年近似算式为ω= 360°* n / 366 ）。

直射点纬度δ，黄赤交角α，黄道角ω三者之间的关系为： sin(β) = sin (α) *sin(ω) ，利用该公式即可计算出太阳直射点的纬度。

（2）地球上某地任意时刻太阳高度角和方位角的计算：建立地心坐标系：Z 轴方向取从地心指向地轴北极的方向，X轴取赤道面与太阳直射经度线平面的交线方向，Y轴取赤道上位于 X轴东侧90°角的方向。

建立本地坐标系：z 轴取垂直地面指向正天顶的方向，x轴取正南方向，y轴取正东方向。

假设某地在地球上的纬度为θ（北纬θ取正值，南纬θ取负值），该地某时刻对应的时间角为φ（φ为当地经度与太阳直射经度之间的差值，φ每小时转过的角度为15°，φ的大小可以利用该时刻与当地正午时刻的时间差 t 表示，公式为：φ = 15°* t ，t 的单位为小时，上午 t 取负值，下午 t取正值），则地心坐标系与本地坐标系之间的转化关系为：x = X* sin(θ)*cos(φ) +Y*sin(θ)*sin(φ) - Z*cos(θ) ，y = - X*sin(φ) + Y*cos(φ) ，z = X*cos(θ)*cos(φ) + Y* cos(θ)*sin(φ) + Z*sin(θ) 。

设当天的太阳的直射点纬度为δ，则太阳直射点的位置矢量在地心坐标系中的表达式 S = cos(δ) * i + sin(δ) * k ，则由两个坐标系的转化关系可得到太阳直射点位置矢量在本地坐标系中的表达式为 S =[ cos(δ)*sin(θ)*cos(φ) - sin(δ)*cos(θ) ] * i +[ - cos(δ)*sin(φ) ] * j + [ cos(δ)*cos(θ)*cos(φ) +sin(δ)*sin(θ) ] * k 。

求太阳升起的方位角广东省佛山市顺德区一中刘华新太阳从何方升起，这似乎是一个再简单不过的问题，一般人会不假思索地回答是从东方升起。

从总体上来说，这也是对的，但是这种情况只能是说从全年的平均情况看是这样的。

对于我们有了一定的地理知识，特别是有了地球运动、地平圈、方位角、天球概念有关知识的人来说就不能简单地这么认为了。

实际上在不同的季节、不同的纬度，太阳升起的方位角是不同的，不一定是从正东方升起。

在夏季时，较高纬度地区太阳可以从东偏北50°到60°甚至更高角度升起，在西偏北同样的角度落下；冬季时可以从东偏南50°或者更多升起，在西偏南50°或以上落下。

这时候我们还能说太阳是从东方升起吗？显然不能这么说。

所以我们在夏天时可以说：“一轮红日从东北方升起，在西北方落下”。

那么怎样来准确计算太阳升起的方位角呢？这里我们来推导一个计算公式，把地理概念和数学中的立体几何知识结合起来就不难解决这个问题了。

例：当太阳直射北纬20度时，求北纬30度地区太阳升起的方位角。

具体解决这个问题我想可以通过下面的8个步骤来解决和说明（1）我们可绘如下的图图一设观测者在北纬30度线上的某一点A点上，则D圈为A点所在的地平圈（注意地平圈一定与观测点A点到地心O的连线是垂直的，另外由图中可看出地平圈与赤道平面的夹角即二面角为60度）。

地平圈和赤道（这里理解为天赤道）的交点E为正东方（东点）、交点W为正西方（西点）。

另外，N为正北、S为正南、O为地心。

（2）还是见上面的图（图一），设地平圈与北纬20°的交点为B。

由于太阳直射在北纬20°线上，随着地球的自转，总有一刻太阳会直射到B点，光线同时指向地心O，太阳和地平圈在同一平面上，这时候A点的人太阳刚好可看到太阳升起。

（为什么这样说呢？这里我们要引入天球的概念，地平圈和赤道都无限延伸与天球面相交，在天球尺度上，地球可以认为是一个点，位于天球的中心。

太阳方位角/高度角计算公式2014/4/14Micheal-Yang1. 太阳高度角sinHs sin sin cos cos cost ϕδϕδ=⋅+⋅⋅式中，表示太阳高度角，表示地理纬度，表示太阳赤纬，表示时角。

(太阳赤纬和时角的概念请自行百度。

)由式中可见，地理纬度，还需要求太阳赤纬和时角。

太阳赤纬和时角的求法见下。

2. 太阳方位角()()/cosAs sinHs sin sin cosHs cos ϕδϕ=⋅−⋅式中，表示太阳高度角，表示地理纬度，表示太阳赤纬。

3. 太阳赤纬设太阳赤纬为delta ，有：delta(deg)=[0.006918-0.399912cos(b)+0.070257sin(b)-0.006758cos(2b)+0.000907sin(2b)-0.002697cos(3b)+0.00148sin(3b)](180/pi)其中delta 的单位为度(deg)；pi=3.1415926为圆周率；b(deg)=360N/365，单位为度(deg)； N 为日数，自每年1月1日开始计算。

4. 时角时角由太阳时求得。

太阳时角在正午时约为零，上午为负，下午为正，日出时约为-90°，日没时约为90°。

平均每小时时角变化15°。

太阳时角t = ( 真太阳时(called True Time) - 12 ) * 15°我们知道，一般情况下，我们的时钟显示12:00时，太阳并没有位于正中间，这是因为我们的时钟时间(也叫“平太阳时”)与真太阳时有一定的偏差，而真太阳时的12:00正是太阳位于正中，即方位角为0的时间。

真太阳时=平太阳时+真太阳时时差。

还有一点我们要注意，由于我国全国使用的都是“北京时间”，因此在计算真太阳时时，还要计算由于经度不同带来的时差。

虽然是“北京时间”，但“北京时间”是根据东经120°测得的，因此计算时差时，要以东经120°为标准。

太阳方位角计算公式是什么太阳方位角计算公式是什么太阳方位角是太阳所在的方位，有很多的高中生不知道太阳方位角的计算方法。

下面是店铺为你精心推荐的太阳方位角计算公式的内容，希望对您有所帮助。

太阳方位角计算公式太阳高度角hs：sinhs=sinφ·sinδ+cosψ·cosδ·cosΩ式中 hs-太阳高度角φ-地理纬度δ-赤纬Ω-时角2,求太阳方位角AsCOSAs= sinhs·sinψ-sinδ/(coshs·cosψ)As-太阳方位角太阳方位角的测定方法对于中国区域，早上太阳光从东边射来，中午太阳光从南边射来，傍晚太阳光从西边边射来，早上的太阳方位角在90°左右(但一年当中，有一定的角度范围变化)，正中午的太阳方位角在180°(正南方)，傍晚的太阳方位角在270°左右(但一年当中，有一定的角度范围变化)。

例如北京处在北纬约40°，一年中，早上的.太阳方位角变化量约为90°±31°。

对于陆地卫星系统而言，如美国的Landsat TM/ETM+，该卫星的过境(中国)时间大概是早上到中午之间，因此其太阳方位角一般在0°和90°之间。

对于地球上任何位置，当太阳处于春分点或秋分点，即太阳赤纬是0°的时候，初升的太阳方位角是90°整，正午太阳方位角是180°，落日的时候太阳方位角是270°。

对北半球而言，当太阳赤纬大于0°的时候太阳从东偏北方向升起，此时太阳方位角小于90°，中午180°，落日时太阳方位角大于270°。

当太阳赤纬小于0°的时候太阳从东偏南方向升起，此时太阳方位角大于90°，中午180°，落日时太阳方位角小于270°。

日地距离计算公式地球绕太阳公转的轨道是椭圆形的，太阳位于椭圆两焦点中的一个。

太阳方位角变化规律一、引言在地球上，太阳是我们最重要的能量来源之一。

太阳方位角是指太阳在地平面上的位置与正南方向之间的夹角。

太阳方位角的变化规律对于许多领域都具有重要意义，如太阳能利用、天文观测、导航等。

本文将探讨太阳方位角随时间的变化规律，并分析其影响因素和应用。

二、太阳方位角的基本概念在地球上的任意一个位置，在一天中不同的时间，太阳的位置是不同的。

太阳方位角是用来描述太阳位置的参数之一。

太阳方位角的单位通常以度数来表示，其中正南方向为0度，正西方向为90度，正北方向为180度，正东方向为270度。

三、太阳方位角的变化规律太阳方位角的变化规律主要受到以下几个因素的影响：1. 季节的影响随着季节的变化，太阳方位角也会不断变化。

在春分和秋分时，太阳直射赤道，此时太阳方位角在正南方向上。

在夏至时，太阳在北回归线上，太阳方位角在正北方向上。

在冬至时，太阳在南回归线上，太阳方位角在正南方向上。

因此，随着季节的变化，太阳方位角也会相应改变。

2. 时间的影响在一天中不同的时间，太阳方位角也会发生变化。

在中午时分，太阳的位置最高，太阳方位角在正南方向上。

在早晨和傍晚时分，太阳的位置较低，太阳方位角在东方或西方。

而在夜间，太阳方位角无法测量，因为太阳已经下山。

3. 纬度的影响地球上不同纬度的地区，太阳方位角也有所不同。

在赤道附近的地区，太阳方位角变化不大，基本在正南方向上。

而在极地地区，太阳方位角变化非常大，甚至出现极夜和极昼的现象。

四、太阳方位角的计算方法太阳方位角的计算方法主要有几种，其中比较常用的是太阳高度角和方位角的计算方法。

太阳高度角是指太阳光线与地平面夹角，可以通过观测太阳的仰角来计算。

太阳方位角可以通过太阳高度角和太阳时角的计算来获得。

太阳时角是指太阳与地球表面上某一点的子午线（正南北方向）之间的夹角，可以通过观测太阳通过地方子午线的时间来计算。

五、太阳方位角的应用太阳方位角的变化规律在许多领域都有广泛的应用，以下是其中一些常见的应用：1. 太阳能利用太阳能是一种清洁、可再生的能源，通过利用太阳能可以发电、供热等。

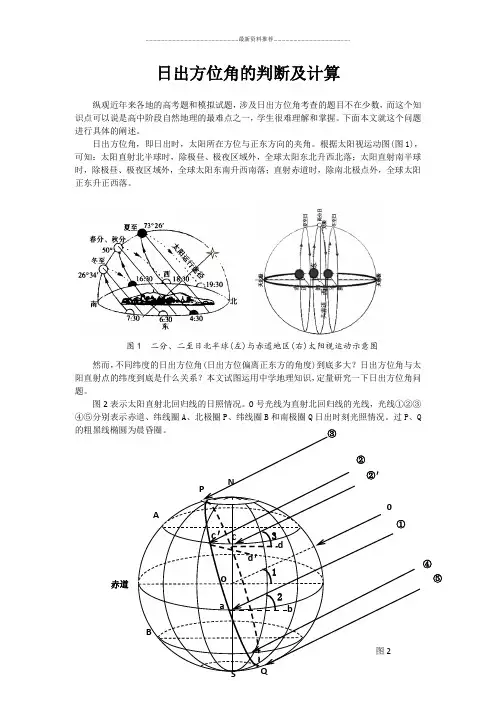
日出方位角的判断及计算纵观近年来各地的高考题和模拟试题，涉及日出方位角考查的题目不在少数，而这个知识点可以说是高中阶段自然地理的最难点之一，学生很难理解和掌握。

下面本文就这个问题进行具体的阐述。

日出方位角，即日出时，太阳所在方位与正东方向的夹角。

根据太阳视运动图(图1)，可知：太阳直射北半球时，除极昼、极夜区域外，全球太阳东北升西北落；太阳直射南半球时，除极昼、极夜区域外，全球太阳东南升西南落；直射赤道时，除南北极点外，全球太阳正东升正西落。

然而，不同纬度的日出方位角(日出方位偏离正东方的角度)到底多大？日出方位角与太阳直射点的纬度到底是什么关系？本文试图运用中学地理知识，定量研究一下日出方位角问题。

图2表示太阳直射北回归线的日照情况。

0号光线为直射北回归线的光线，光线①②③④⑤分别表示赤道、纬线圈A、北极圈P、纬线圈B和南极圈Q日出时刻光照情况。

过P、Q图1 二分、二至日北半球(左)与赤道地区(右)太阳视运动示意图③c′c′①②②′④⑤ABN赤道P123a bcdoc′d′一、赤道地区日出方位角的大小1、赤道夏至时的日出方位角的计算如图2，∵太阳直射北回归线∴∠1=23°26′辅助线ab与赤道共面，且在晨昏圈与赤道的交点a上与赤道相切。

直线ab与光线①的夹角为∠2又∵所有太阳光线均为彼此平行的射线，∴∠2=∠1=23°26′∠2=23°26′的地理意义：夏至时，赤道地区日出方位为东偏北23°26′。

2、推论：赤道地区日出方位角(日出方位偏离正东方的角度)的度数与太阳直射点的纬度度数相等。

赤道地区，冬至时太阳直射23°26′S，日出方位角为23°26′，日出方位为东偏南23°26′。

春秋分时太阳直射赤道，日出方位角为00，日出方位为正东。

二、其它纬度日出方位角的大小变化规律1、夏至日其它纬度日出方位角的计算如图2，辅助线cd、ef分别与纬线圈A、纬线圈B共面，且在地方时为6：00的经线与纬线圈A和纬线圈B的交点c、e处与纬线圈相切。

太阳位置求算公式与计算举例默认分类2022-11-14 21:04:44阅读393评论2 字号：大中小订阅太阳位置求算公式与计算举例杨齐聪在新农村建设和城市高楼群落的规划设计中，为了解决土地采用率与满意采光通风最低要求的冲突，常会遇到各幢楼房各部位的采光时间和日墙方位角的计算。

太阳位置可由太阳高度角hs和方位角as打算，依据球面三角基本公式可得：一、太阳高度角hs求算公式Sinhs=sinδsinφ+cosδcosφcosω (1)式中δ为太阳赤纬，表示太阳光线与地球赤道面的夹角，一年四季每天都在变动着，冬至B δ=-23o27,,春分日和秋分日δ=0°,夏至日5二23。

27'；φ为测点纬度,如北京φ=39°48'∖西安φ=34°18;上海φ=31o10∖杭州φ=30°19;临海φ=28°51'∖福州φ=26°05'∖台北φ=25°20'∖广州φ=23°08∖3为太阳时角，以当地正午为0。

，上午为负，每小时一15。

，下午为正，每小时+15。

，ω在赤道面上每小时变化为=15°, 3所表示的是真太阳时;与时钟不同。

现举例计算于下：1.求北纬30。

地方冬至日正午时刻和下午1时、2时(均指地方时)的太阳高度角。

①正午时刻太阳时角为0。

，即3=0°将5=—23°27'、φ=30∖ 3=0。

代入(1)式得Sinh !E^=sin(-23027,)sin300+cos(-23027,)cos300cos00=-0.3979×0.5+0.9175×0.8660×1=-0.19895+0.79456=0.5956h正午=36°33'(查正弦数学用表所得，下同)则北纬30。

地方冬至日正午时刻的太阳高度角为36。

33：②下午1时(上午11时与此高度角同)，太阳时角为15°,即ω=15o得Sinh 下午 1 0'J =sin(-23o27,)si∩3O o+cos(-23o27,)cos3O o cos15°=-0.19895+0.79456×0.9659=-0.19895+0.7675=0.5685h下午1时二34°39'则北纬30。