数学建模2008年D题-(NBA赛程分析)

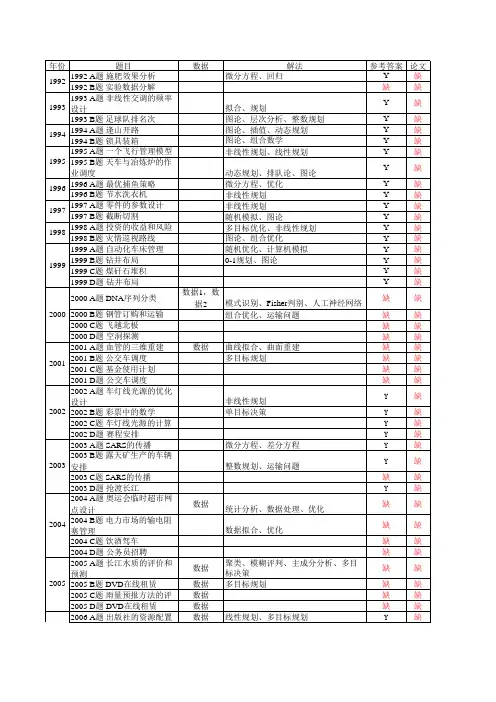
全国大学生数学建模竞赛历年赛题1992：A?施肥效果分析 B?实验数据分解1993：A?非线性交调的频率设计 B?足球队排名次1994：A?逢山开路 B?锁具装箱1995：A?一个飞行管理问题 B?天车与冶炼炉的作业调度1996：A?最优捕鱼策略 B?节水洗衣机1997：A?零件参数 B?截断切割1998：A?投资的收益和风险 B?灾情巡视路线1999：A?自动化车床管理 B?钻井布局 C?煤矸石堆积 D?钻井布局2000：A?DNA序列分类 B?钢管购运 C?飞越北极 D?空洞探测2001：A?血管三维重建 B?公交车调度 C?基金使用2002：A?车灯线光源 B?彩票中数学 D?赛程安排2003：A?SARS的传播 B?露天矿生产 D?抢渡长江2004：A?奥运会临时超市网点设计 B?电力市场的输电阻塞管理C?饮酒驾车 D?公务员招聘2005：A 长江水质的评价和预测 B?DVD在线租赁C?雨量预报方法的评价 D?DVD在线租赁?2006：A出版社的资源配置 B 艾滋病疗法的评价及疗效的预测C易拉罐形状和尺寸的最优设计D 煤矿瓦斯和煤尘的监测与控制2007：A 中国人口增长预测 B 乘公交，看奥运C 手机“套餐”优惠几何D 体能测试时间安排2008：A 数码相机定位 B 高等教育学费标准探讨C 地面搜索D NBA赛程的分析与评价2009：A 制动器试验台的控制方法分析 B 眼科病床的合理安排C 卫星和飞船的跟踪测控 D会议筹备2010：A储油罐的变位识别与罐容表标定B 2010年上海世博会影响力的定量评估C输油管的布置D对学生宿舍设计方案的评价2011: A 城市表层土壤重金属污染分析B 交巡警服务平台的设置与调度C 企业退休职工养老金制度的改革D 天然肠衣搭配问题2012: A 葡萄酒的评价B 太阳能小屋的设计C 脑卒中发病环境因素分析及干预D 机器人避障问题2013: A 车道被占用对城市道路通行能力的影响B 碎纸片的拼接复原C 古塔的变形D 公共自行车服务系统2014: A 嫦娥三号软着陆轨道设计与控制策略B 创意平板折叠桌C 生猪养殖场的经营管理D 储药柜的设计2015: A ?太阳影子定位B?“互联网+”时代的出租车资源配置C? 月上柳梢头D? 众筹筑屋规划方案设计。

NBA赛程的分析与评价
张德全
【期刊名称】《桂林航天工业学院学报》
【年(卷),期】2009(014)002
【摘要】针对2008年全国大学生数学建模竞赛D题 "NBA赛程的分析与评价"问题,得到赛程安排对某一球队的利弊主要因素有三个方面:相邻两场比赛间隔天数,连续客场数、旅程总数.通过2007-2008赛季赛程计算时间间隔利弊指标、连续客场利弊指标、旅程利弊指标与该赛季各球队总战绩的相关系数,给出2008-2009NBA 赛程的分析与评价,并得到赛程选取赛3场球队的改进方案.
【总页数】5页(P242-246)
【作者】张德全
【作者单位】桂林航天工业高等专科学校,计算机系,广西,桂林,541004
【正文语种】中文
【中图分类】O213.9
【相关文献】
1.利用层次分析法对NBA赛程的分析与评价 [J], 童伟;杜吉梁
2.NBA赛程分析与评价 [J], 王红霞;张力;任志淼
3.关于NBA赛程利弊因素的分析与评价模型 [J], 周密
4.基于Matlab的NBA赛程分析与评价模型 [J], 赵小云;沈陆娟
5.NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目 [J], 马明远
因版权原因，仅展示原文概要，查看原文内容请购买。

NBA赛程的分析与评价的数学模型
邱崇洋;肖芸芸
【期刊名称】《中国新技术新产品》
【年(卷),期】2008(000)018
【摘要】本文依据NBA2008-2009赛季常规赛的赛程安排表,运用数据统计的原理建立起数学模型,通过大量的数据处理,研究分析了新赛季的赛程安排分别对其30支球队的影响,并找出了安排同部不同区球队比赛的方法而且还设计出了更为合理的安排方法。

【总页数】1页(P192)
【作者】邱崇洋;肖芸芸
【作者单位】江西理工大学应用科学学院,江西赣州341000
【正文语种】中文
【中图分类】O141.4
【相关文献】
1.利用层次分析法对NBA赛程的分析与评价
2.层次分析下的NBA赛程分析与评价模型
3.关于NBA赛程利弊因素的分析与评价模型
4.NBA赛程分析与评价数学模型的构建
5.NBA赛程分析与评价的数学模型
因版权原因，仅展示原文概要，查看原文内容请购买。

赛程安排的数学模型与分析1．前言n支球队在同一场地上进行单循环赛有多种赛程安排，问题是如何编制符合公平性的赛程，数学上这是一个满足一定指标要求的配对排序问题。

本文在合理假设的基础上，由问题的数学实质，建立出问题的线性规划模型；由问题的特殊性将n分为偶数与奇数分别研究，获得关于各队每两场比赛之间相隔场次数上限的一般公式，用构造性方法加以证明；运用归纳的方法发现了这种特殊排序中的对称规律，由此设计出符合上限要求的计算机算法与实际人工编制法。

文中对赛程优劣的评价指标也作了较多的探讨。

本文一个特点是，分析研究迄今体育界实际使用的赛程“循环编制法”，发现其对n为奇数时编制的赛程公平性差，给出了一种n 为奇数时编制简便、结果合理的人工编制法。

2．问题的提出你所在的年级有5个班，每班一支球队在同一块场地上进行单循环赛, 共要进行10场比赛. 如何安排赛程使对各队来说都尽量公平呢. 下面是随便安排的一个赛程: 记5支球队为A, B, C, D, E，在下表左半部分的右上三角的10个空格中, 随手填上1,2,⋯10, 就得到一个赛程, 即第1场A对B, 第2场B对C, ⋯, 第10场C对E. 为方便起见将这些数字沿对角线对称地填入左下三角.这个赛程的公平性如何呢, 不妨只看看各队每两场比赛中间得到的休整时间是否均等. 表的右半部分是各队每两场比赛间相隔的场次数, 显然这个赛程对A, E有利, 对D则不公平.从上面的例子出发讨论以下问题:1) 对于5支球队的比赛, 给出一个各队每两场比赛中间都至少相隔一场的赛程.2) 当n支球队比赛时, 各队每两场比赛中间相隔的场次数的上限是多少.3) 在达到2) 的上限的条件下, 给出n=8, n=9的赛程, 并说明它们的编制过程.4) 除了每两场比赛间相隔场次数这一指标外, 你还能给出哪些指标来衡量一个赛程的优劣, 并说明3) 中给出的赛程达到这些指标的程度.赛程安排直接影响比赛的公平性，如何建立衡量一个赛程的优劣的指标，建立编制公平合理的排列问题的数学研究，也有数学意义。

模型定性指标量化的应用案例：（1）CUMCM2003-A,C:SARS的传播问题（2）CUMCM2004-D:公务员招聘问题；（3）CUMCM2005-B:DVD租赁问题；（4）CUMCM2008-B:高教学费标准探讨问题；（5）CUMCM2008-D:NBA赛程的分析与评价问题；（6）CUMCM2009-D:会议筹备问题。

综合评价方法：线性加权综合法、非线性加权综合法、逼近理想点（topsis）法的应用案例（1）CUMCM1993-B:足球队排名问题；（2）CUMCM2001-B:公交车调度问题；（3）CUMCM2002-B:彩票中的数学问题；（4）CUMCM2004-D:公务员招聘问题；（5）CUMCM2005-A:长江水质的评价和预测问题；（6）CUMCM2005-C:雨量预报方法评价问题；（7）CUMCM2006-B:艾滋病疗法评价与预测问题；（8）CUMCM2007-C:手机“套餐”优惠几何问题；（9）CUMCM2008-B:高教学费标准探讨问题；（10）CUMCM2008-D:NBA赛程的分析与评价问题；（11）CUMCM2009-D:会议筹备问题。

动态加权与综合排序的应用案例动态加权的综合排序案例：（1）CUMCM2002-B:彩票中的数学问题；（2）CUMCM2005-A:长江水质的评价和预测问题；综合评价的排序案例：（1）CUMCM1993-B:足球队排名问题；（2）CUMCM2008-D:NBA赛程的分析与评价问题；（3）CUMCM2009-D:会议筹备问题。

数据建模的常用预测方法1插值与拟合方法：小样本内部预测；应用案例：（1）CUMCM2001-A:血管的三维重建问题；（2）CUMCM2003-A,C:SARS的传播问题；（3）CUMCM2004-C:饮酒驾车问题；（4）CUMCM2005-A:长江水质的评价与预测；（5）CUMCM2005-D:雨量预报方法的评价；（6）CUMCM2006-B:艾滋病疗法的评价与预测。

全国大学生数学建模竞赛历年试题1.1992年A题：施肥效果分析；B题：试验数据分析；2.1993年A题：非线性交调的频率设计；B题：足球队拍名次；3.1994年A题：逢山开路；B题：锁具开箱；4.1995年A题：一个飞行管理问题；B题：天车与冶炼炉的作业调度；5.1996年A题：最优捕鱼策略；B题：节水洗衣机；6.1997年A题：零件的参数设计；B题：截断切割；7.1998年A题：投资的收益和风险B题：灾情巡视路线8.1999年A题：自动化车床管理B题：钻井布局C题：煤矸石堆积D题：钻井布局9.2000年A题：DNA序列分类B题：钢管订购和运输C题：飞越北极D题：空洞探测10.2001年A题：血管的三维重建B题：公交车调度C题：基金使用计划D题：公交车调度11.2002年A题：车灯线光源的优化设计B题：彩票中的数学C题：车灯线光源的计算D题：赛程安排12.2003年A题：SARS的传播B题：露天矿生产的车辆安排C题：SARS的传播D题：抢渡长江13.2004年A题：奥运会临时超市网点设计B题：电力市场的输电阻塞管理C题：饮酒驾车D题：公务员招聘14.2005年A题：长江水质的评价和预测B题：DVD在线租赁C题：雨量预报方法的评价D题：DVD在线租赁15.2006年A题：出版社的资源配置B题：艾滋病疗法的评价及疗效的预测C题：易拉罐形状和尺寸的最优设计D题：煤矿瓦斯和煤尘的监测与控制16.2007A题：中国人口增长预测；B题：乘公交，看奥运；C题：手机“套餐”优惠几何；D题：体能测试时间安排17.2008A题数码相机定位;B题高等教育学费标准探讨;C题地面搜索;D题NBA赛程的分析与评价.18.2009A题制动器试验台的控制方法分析B题眼科病床的合理安排C题卫星和飞船的跟踪测控D题会议筹备19.2010A题储油罐的变位识别与罐容表标定B题2010年上海世博会影响力的定量评估C题输油管的布置D题对学生宿舍设计方案的评价19.2011A题城市表层土壤重金属污染分析B题交巡警服务平台的设置与调度C题企业退休职工养老金制度的改革D题天然肠衣搭配问题20.2012A题葡萄酒的评价B题太阳能小屋的设计C题脑卒中发病环境因素分析及干预D题机器人避障问题21.2013 A题车道被占用对城市道路通行能力的影响B题碎纸片的拼接复原C题古塔的变形D题公共自行车服务系统。

NBA赛程的制定和评价数学建模报告专业：电子信息工程学号: 0731432707314314姓名：喻琨闵龙骥指导老师：黄雯完成时间：2008-12-25NBA赛程的制定和评价一、问题的重述一个合理的赛程表是NBA能够精彩上演的保证。

维尼克主要负责每支球队的具体赛程的制定，但是无论维尼克如何做，总有一些球队在抱抱怨，他只能尽量使得赛程安排公平合理。

维尼克每个赛季给一支球队定的背靠背上限是24对，下限是15对。

另外，考虑到比赛的观赏性等其他一些因素，由于历史原因，有些球队之间的比赛会格外引人注目，同样的，球队内的球星也可能成为影响赛程安排的因素，此外，一些节日比赛安排会有所不同，很明显周末比赛相对紧密，而每个星期天似乎都会有一场精彩的比赛，再比如每年的圣诞大战。

所有这些都在一定程度上增加了比赛安排的复杂性。

要求：对NBA 2007-2008赛季常规赛赛程的安排，讨论其合理性和公平性。

根据问题（1）得出的模型与结论，给出NBA 常规赛赛程安排模型，并制定NBA 2008-2009 赛季的常规赛赛程，并给出评价。

二、模型的基本假设1、假设考察一个赛程安排是否合理主要考虑下面这三个因素：是否满足赛制的要求，球队的满意度，球迷的满意度。

2、假设个球队的排名情况和拥有的球星数能够说明该队的受关注程度。

3、假设各球队对赛程的满意度仅取决于对“主客场数”和“背靠背数”的满意度。

4、假设球迷对赛程的满意程度主要取决于重要比赛的安排时间。

5、假设08—09季度的比赛每个周末比赛日的比赛场数固定，非周末比赛日比赛场数大体相等。

6、假设在对08—09赛季的赛程安排时，只考虑节假日里不安排比赛，不考虑其他因素的比赛的影响。

三、符号说明符号表示的意义记录2007—2008赛季各场比赛信息的的矩阵存储个球队在2007—2008赛季客场比赛数的数组存储各球队在2007—2008赛季背靠背比赛数的数组记录30支球队再2007—2008赛季排名信息的的矩阵第队与第队到第天为止，队为主场，队为客场的两队的交锋次数和的不分主客场的交锋次数描述对阵形势及对应对阵形势下比赛场数的矩阵队客场挑战队的对阵形式队和队在这种对阵形式下进行的对赛场数队和队比赛的精彩系数每个赛季的比赛观赏系数与每场比赛观赏性系数的和球队对主客场数的满意度球队对背靠背数的满意度第支球队的整体实力系数第支球队的打比赛时的精彩系数将队客场挑战队这场比赛映射为一个数值的函数四、问题的分析和模型的建立问题一模型建立对于每个赛程的合理性和公平性，可由下面3个主要因素来衡量：A四条硬性的要求1）每个分区的球队在常规赛中要与在同一个分的球队比赛四场2）分区的每支球队要与分区以外，但是在同在一个大赛区的每个球队相遇三到四次3）小赛区的每支球队要与不同大赛区的每支球队比赛两场4）共用同一个比赛场馆的球队的主场比赛不能在同一天进行。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：NBA赛程的分析与评价摘要本文所要研究的是在给定NBA赛程的情况下，如何运用数学方法，通过结合各支球队的情况深入分析赛程安排对各球队的影响，同时还要对影响的好坏作出评价的问题。

赛程的安排对一支球队比赛的利弊有很多影响因素，本文根据实际比赛中对联赛战绩有的影响因素，提出了连续客场，背靠背，连续与强队的比赛的三个主要影响因素。

将赛程安排利用表格、程序等进行量化处理，并按各队的强弱进行一个排序和编号，给出各个因素的量化值并进行标准化。

利用层次分析法确定了各个因素的权重，用公式将权重和各因素的值综合，给出赛程利弊的综合值。

对于问题二，利用问题一所得出利弊的综合指数，按照排序找出火箭队的利弊，和最有利、最不利的球队。

问题三中对2007至2008年赛程表分析找出赛3场的方法。

按两对实力差大的赛3场的原则，对同部不同区的队之间，利用胜率差找出新的赛三场的方法予以比较，找出原方法的优缺点，并给与评价。

2008高教社杯全国大学生数学建模竞赛题目 （请先阅读“全国大学生数学建模竞赛论文格式规范”）A题数码相机定位数码相机定位在交通监管（电子警察）等方面有广泛的应用。

所谓数码相机定位是指用数码相机摄制物体的相片确定物体表面某些特征点的位置。

最常用的定位方法是双目定位，即用两部相机来定位。

对物体上一个特征点，用两部固定于不同位置的相机摄得物体的像，分别获得该点在两部相机像平面上的坐标。

只要知道两部相机精确的相对位置，就可用几何的方法得到该特征点在固定一部相机的坐标系中的坐标，即确定了特征点的位置。

于是对双目定位，精确地确定两部相机的相对位置就是关键，这一过程称为系统标定。

标定的一种做法是：在一块平板上画若干个点，同时用这两部相机照相，分别得到这些点在它们像平面上的像点，利用这两组像点的几何关系就可以得到这两部相机的相对位置。

然而，无论在物平面或像平面上我们都无法直接得到没有几何尺寸的“点”。

实际的做法是在物平面上画若干个圆（称为靶标），它们的圆心就是几何的点了。

而它们的像一般会变形，如图1所示，所以必须从靶标上的这些圆的像中把圆心的像精确地找到，标定就可实现。

图 1 靶标上圆的像有人设计靶标如下，取1个边长为100mm的正方形，分别以四个顶点（对应为A、C、D、E）为圆心，12mm为半径作圆。

以AC边上距离A点30mm处的B为圆心，12mm为半径作圆，如图2所示。

图 2 靶标示意图用一位置固定的数码相机摄得其像，如图3所示。

图3 靶标的像请你们：（1） 建立数学模型和算法以确定靶标上圆的圆心在该相机像平面的像坐标, 这里坐标系原点取在该相机的光学中心，x-y平面平行于像平面；（2） 对由图2、图3分别给出的靶标及其像，计算靶标上圆的圆心在像平面上的像坐标, 该相机的像距（即光学中心到像平面的距离）是1577个像素单位(1毫米约为3.78个像素单位)，相机分辨率为1024×768；（3） 设计一种方法检验你们的模型，并对方法的精度和稳定性进行讨论；（4） 建立用此靶标给出两部固定相机相对位置的数学模型和方法。

NBA赛程的分析与评价摘要本文首先综合考虑了NBA上个赛季的赛程、赛绩和本赛季的赛程确定出赛程对球队利弊的三个主要影响因素，并对其进行了定量分析。

其次利用偏大型柯西分部隶属函数确定主要影响因素的权值，给出了一个利弊的评价指标——利弊指数，并计算了各球队的利弊指数值。

从得到的结果看本次赛程对火箭队而言是比较有利的，其中最有利的球队是凯尔特人队，最不利的是快船队。

对于问题三，基于公平性和观赏性考虑，同部不同区球队实力尽可能悬殊的队尽可能少赛（赛3场）。

由此建立0-1规划模型，并利用LINDO软件求解出了赛3场球队的最优选取方案。

关键词：隶属函数利弊指数 0-1规划一.问题的重述NBA赛程的安排对球队实力的发挥和战绩存在着客观的影响，但编制一个完整的、对各球队尽可能公平的赛程是一件非常复杂的事情。

为了更直观的体现出这些客观因素的存在，利用数学建模方法对2008～2009年的赛季安排表进行定量的分析与评价：1）确定出赛程对某一支球队的利弊的主要影响因素，根据所确定的因素将赛程转换为便于进行数学处理的数字格式，同时给出评价赛程利弊的数量指标。

2）按照1）的结果计算、分析赛程对火箭队的利弊，并找出赛程对30支球队最有利和最不利的球队。

3）对2008～2009年的赛季安排表进行分析可以发现，每支球队与同区的每一支球队赛4场（主客各2场），与不同部的每一球队赛2场（主客各1场），与同部不同区的每一球队有赛4场和赛3场（2主1客或2客1主）两种情况，每支球队的主客场数量相同且同部3个区的球队间保持均衡。

试根据赛程找出与同部不同区球队比赛中，选取赛3场的球队的方法。

这种方法如何实现，对该方法给予评价，也可以给出认为合适的方法。

二.问题分析问题1首先应综合分析上一赛季的赛绩和本次赛季的赛程确定赛程对球队利弊的主要影响因素，其次要确定影响因素权值；根据本次赛场各球队的影响指标，对东西联盟的30支球队进行排序。

问题2根据上一问所得的结果，重点分析赛程对火箭队的利弊及赛程对那个队是最有利的，对那个队是最不利的。

全国大学生数学建模竞赛的历年赛题（1992年—2011年）1992年:(Ａ)作物生长的施肥效果问题(北理工：叶其孝）(B)化学试验室的实验数据分解问题（复旦：谭永基）1993年:(Ａ)通讯中非线性交调的频率设计问题（北大:谢衷洁）(Ｂ)足球甲级联赛排名问题（清华：蔡大用）1994年:(Ａ)山区修建公路的设计造价问题（西电大：何大可）(Ｂ)锁具的制造、销售和装箱问题（复旦:谭永基等）1995年:(Ａ)飞机的安全飞行管理调度问题（复旦:谭永基等）(Ｂ)天车与冶炼炉的作业调度问题（浙大:刘祥官等）1996年:(A)最优捕鱼策略问题（北师大：刘来福）(B)节水洗衣机的程序设计问题（重大：付鹂）1997年:(A)零件参数优化设计问题（清华：姜启源）(B)金刚石截断切割问题（复旦：谭永基等）1998年:(A)投资的收益和风险问题（浙大：陈淑平）(B)灾情的巡视路线问题（上海海运学院:丁颂康）1999年:(A)自动化机床控制管理问题（北大：孙山泽）(B)地质堪探钻井布局问题（郑州大学：林诒勋）(C)煤矸石堆积问题（太原理工大学：贾晓峰）(D)钻井布局问题2000年:(A)DNA序列的分类问题（北工大：孟大志）(B)钢管的订购和运输问题（武大：费甫生）(C)飞越北极问题（复旦：谭永基）(D)空洞探测问题（东北电力学院：关信）2001年:(A)三维血管的重建问题（浙大：汪国昭）(B)公交车的优化调度问题（清华：谭泽光）(C)基金使用计划问题（东南大学：陈恩水）(D)公交车调度问题2002年:(A)汽车车灯的优化设计问题（复旦:谭永基等）(B)彩票中的数学问题（信息工程大学：韩中庚）(C)车灯线光源的计算问题(D)球队的赛程安排问题（清华：姜启源）2003年:(A)SARS的传播问题（集体）(B)露天矿生产的车辆安排问题（吉林大：方沛辰）(C)SARS的传播问题(D)抢渡长江问题（华中农大：殷建肃）2004年:(A)奥运会临时超市网点设计问题(北工大：孟大志)(B)电力市场的输电阻塞管理问题(浙大:刘康生）(C)酒后开车问题（清华：姜启源）(D)公务员的招聘问题（信息工程大学：韩中庚）2005年:(A)长江水质的评价与预测问题（信息工大:韩中庚）(B)DVD在线租赁问题（清华：谢金星等）(C)雨量预报方法的评价问题（复旦：谭永基）(D)DVD在线租赁问题2006年:(A)出版社的资源管理问题（北工大:孟大志）(B)艾滋病疗法的评价及预测问题（天大：边馥萍）(C)易拉罐形状和尺寸的设计问题（北理工：叶其孝）(D)煤矿瓦斯和煤尘的监测与控制问题（信息工程大学：韩中庚）2007年: (A)中国人口增长预测问题(B) 乘公交，看奥运问题(C) 手机“套餐”优惠几何问题(D) 体能测试时间安排问题2008年：(A) 数码相机定位问题(B) 高等教育学费标准探讨问题(C) 地面搜索问题(D) NBA赛程的分析与评价问题2009年：(A) 制动器试验台的控制方法分析问题(B) 眼科病床的合理安排问题(C) 卫星和飞船的跟踪测控问题(D) 会议筹备问题2010年：(A) 储油罐的变位识别与罐容表标定问题(B) 2010年上海世博会影响力的定量评估问题(C) 输油管的布置问题(D) 对学生宿舍设计方案的评价问题2011年：(A) 城市表层土壤重金属污染分析问题(B) 交巡警服务平台的设置与调度问题(C) 企业退休职工养老金制度的改革问题(D) 天然肠衣搭配问题问题。

NBA赛程评价【摘要】本问题研究的是NBA球赛的赛程安排对球队的利弊影响，对数据进行量化处理，采用分层次的办法分析各个因素对球队的利弊影响，再利用0-1变量确定球队打3场的分配情况，建立最优化模型。

问题一：分析赛程安排对球队的利弊影响，列出影响球队利弊的因素，根据各个影响因素的重要程度进行分层次的方法分别分析，得到影响各个球队的利弊的权重。

最后根据各个因素的分析情况进行汇总，统筹规划出总的影响球队利弊的分析指标和算法。

问题二：本问题建立在问题一的基础上，首先利用问题一中的指标和算法进行有针对性的数据处理，并计算得到各个球队总体的利弊权重，对各个球队的利弊权重进行比较，值最小的为最有利的球队是凯尔特人队，值最大的也就是最差的为热火队，最后再分别根据总体和分层次的利弊权值对火箭总体和各个月份的利弊情况进行分析评价。

问题三：分析此问题，在球赛分配的同部不同区内有赛3场和赛4场两种情况，要求给出分配办法，属于已知答案推导算法的过程，我们可以利用排除法，将各个可能影响排法的因素分别用数据求证，最后证明是根据球队实力结合区区之间平衡进行粗略分配的，最后我们依然根据这两个因素，建立最优化模型，利用LINGO进行求解得出更优化的排法，答案见表（九）。

关键词：层次分析最优化权重一问题重述1．1问题背景NBA是全世界篮球迷们最钟爱的赛事之一，姚易加盟以后更是让中国球迷宠爱有加。

NBA共有30支球队，西部联盟、东部联盟各15支，大致按照地理位置，西部分西南、西北和太平洋3个区，东部分东南、中部和大西洋3个区，每区各有5支球队。

对于2008~2009新赛季，常规赛阶段从2008年10月29日（北京时间）直到2009年4月16日，在这5个多月中共有1230场赛事，每支球队要进行82场比赛，其中附件1是30支球队2008~2009赛季常规赛的赛程表，附件2是分部、分区和排名情况（排名是2007~2008赛季常规赛的结果）。

2008nba季后赛时间2008nba季后赛赛程2008nba季后赛对阵2008nba季后赛时间2008nba季后赛赛程2008nba季后赛对阵以下是西区首轮完全赛程：注：以下时间均为北京时间洛杉矶湖人VS 丹佛掘金场次时间地点第一场4月21日03:00 洛杉矶第二场4月24日10:30 洛杉矶第三场4月27日05:30 丹佛第四场4月29日10:30 丹佛第五场5月1日待定洛杉矶第六场5月3日待定丹佛第七场5月5日待定洛杉矶新奥尔良黄蜂VS 达拉斯小牛场次时间地点第一场4月20日07:00 新奥尔良第二场4月23日07:00 新奥尔良第三场4月26日08:00 达拉斯第四场4月28日09:30 达拉斯第五场4月30日待定新奥尔良第六场5月2日待定达拉斯第七场5月4日待定新奥尔良圣安东尼奥马刺VS 菲尼克斯太阳场次时间地点第一场4月20日03:00 圣安东尼奥第二场4月23日09:30 圣安东尼奥第三场4月26日10:30 菲尼克斯第四场4月28日03:30 菲尼克斯第五场4月30日待定圣安东尼奥第六场5月2日待定菲尼克斯第七场5月4日待定圣安东尼奥犹他爵士VS 休斯顿火箭场次时间地点第一场4月20日09:30 休斯顿第二场4月22日09:30 休斯顿第三场4月25日10:30 盐湖城第四场4月27日10:30 盐湖城第五场4月30日待定休斯顿第六场5月3日待定盐湖城第七场5月5日待定休斯顿以下是东区首轮完全赛程：注：以下时间均为北京时间波士顿凯尔特人VS 亚特兰大老鹰场次时间地点第一场4月21日08:30 波士顿第二场4月24日08:00 波士顿第三场4月27日08:00 亚特兰大第四场4月29日08:00 亚特兰大第五场5月1日待定波士顿第六场5月3日待定亚特兰大第七场5月5日待定波士顿底特律活塞VS 费城76人场次时间地点第一场4月21日06:00 底特律第二场4月24日07:30 底特律第三场4月26日07:00 费城第四场4月28日07:00 费城第五场4月30日待定底特律第六场5月2日待定费城第七场5月4日待定底特律奥兰多魔术VS 多伦多猛龙场次时间地点第一场4月21日00:30 奥兰多第二场4月23日07:30 奥兰多第三场4月25日07:30 多伦多第四场4月27日03:00 多伦多第五场4月29日07:30 奥兰多第六场5月2日待定多伦多第七场5月4日待定奥兰多克利夫兰骑士VS 华盛顿奇才场次时间地点第一场4月20日00:30 克利夫兰第二场4月22日07:00 克利夫兰第三场4月25日08:00 华盛顿第四场4月28日01:00 华盛顿第五场5月1日待定克利夫兰第六场5月3日待定华盛顿第七场5月5日待定克利夫兰2008冠军杯第一轮淘汰赛2008年2月19-20日2008年3月4-11日（已进行）还有一场国米--利物浦的比赛在3月12日四分之一决赛2008年4月1-2日2008年4月8-9日半决赛2008年4月22-23日2008年4月29-30日决赛2008年5月21日。