异方差的解决方法
- 格式：ppt
- 大小：270.50 KB
- 文档页数：31
下载文档原格式
合集下载
异方差的补救措施
异方差的补救措施1. 考虑使用对数变换或其他非线性变换来减少异方差性。
2. 采用加权最小二乘法，权重与残差的方差成反比。
3. 使用Robust标准误差来处理异方差性。
4. 利用广义最小二乘法(GLS)来估计异方差。
5. 进行异方差稳健的回归分析。
6. 考虑使用白色噪音模型对异方差进行建模。
7. 通过Heteroscedasticity-Consistent标准误差来纠正异方差带来的偏误。
8. 检验残差的自相关结构，尝试消除异方差。
9. 利用广义估计方程(GEE)来处理异方差问题。
10. 进行对残差进行加权以减轻异方差效应。
11. 尝试使用聚类标准误差校正异方差。
12. 使用稳健标准误差修正异方差带来的影响。
13. 采用异方差稳健的假设检验。
14. 借助异方差自回归模型(ARCH/GARCH)来处理异方差问题。
15. 考虑使用面板数据模型来处理异方差。
16. 将数据进行分组来减轻异方差效应。
17. 利用分位数回归来对抗异方差性。
18. 采用bootstrapping方法估计参数，降低异方差的影响。
19. 通过变量变换来消除异方差性，如差分或比率变换。
20. 使用异方差稳健的方差分解技术。
21. 考虑使用时间序列分析方法来处理异方差。
22. 尝试使用交叉验证来验证模型对异方差的适应性。
23. 利用Lagrange乘数检验来识别异方差模型。
24. 考虑使用非参数回归方法来对抗异方差效应。
25. 结合机器学习技术来降低异方差对分析的影响。
26. 利用异方差稳健的置信区间来进行参数估计。
27. 通过重抽样方法来估计模型参数，减轻异方差影响。
28. 考虑采用深度学习技术来预测异方差。
29. 利用奇异谱分析来识别时间序列数据中的异方差性。
30. 使用异方差稳健的模型比较方法。
31. 采用广义自回归条件异方差(GARCH)模型来拟合异方差性。
32. 结合非参数统计方法来应对异方差问题。
33. 通过交叉验证法来比较不同模型对异方差的适应性。
第五章-4异方差的解决方法
11.58966
Log likelihood
-220.1929 F-statistic
29.21043
Durbin-Watson stat 1.149682 Prob(F-statistic) 0.000008
UnWeighted Statistics
WLS处理后的残差图
2000
Hale Waihona Puke 0-2000-4000
补救异方差的基本思路：
变异方差为同方差； 尽量缓解方差变异的程度 为了补救异方差造成的（不再具有最小方差； 参数的显著性检验失效；预 测精度降低）的严重后果
方法：
一、加权最小二乘法
二、对原模型变换的方法
三、“一般解决法”（模型的对数变换）
1、加权最小二乘法的思路
根据离差平方和最小建立起来的OLS法 同方差时：认为各 ei 提供信息的重要程度是一致的，即将各样本点提供的残差一视同仁。 异方差时：离散程度大的ei 对应的回归直线的位置很不精确，拟合直线时理应不太重视 们提供的信息。即 Xi 对应的 ei 偏离大的所提供的信息贡献应打折扣，而偏离小的所提供的 信息贡献则应于重视。因此采用权数对残差提供的信息的重要程度作一番校正，以提高估计 精度。这就是 WLS（加权最小二乘法）的思路。
1
Xi
2
ui Xi
Var
ui Xi
1
X
2 i
Var
ui
2
例2 Yi 1 2 X i ui
Var(ui)
2 i
2
X
i
Yi Xi
1
Xi
2
Xi
ui Xi
Var
ui Xi
1
X
i
stata异方差检验和解决命令
stata异方差检验和解决命令在数据分析中，异方差是一个常见的问题。
异方差指不同样本的方差不相等，这会导致统计结果的不准确性。
Stata提供了许多方法来检验和解决异方差问题。
一、异方差检验检验异方差通常使用Breusch-Pagan-Godfrey(BPG)检验或White检验。
这里以BPG检验为例，该检验的原假设是方差相等，备择假设是方差不相等。
命令格式：estat hettest示例代码：reg y x1 x2 x3estat hettest如果p值小于0.05，则拒绝原假设，说明存在异方差问题。
二、异方差稳健标准误当检测到异方差问题时，可以使用异方差稳健标准误来解决。
异方差稳健标准误在计算系数的标准误时考虑了异方差问题，从而提高了结果的准确性。
命令格式：robust示例代码：reg y x1 x2 x3, robust使用robust命令后，结果中的Standard Error一栏即为异方差稳健标准误。
三、异方差稳健回归如果异方差问题比较严重，只使用异方差稳健标准误可能无法解决问题。
此时可以使用异方差稳健回归。
命令格式：robust示例代码：reg y x1 x2 x3, vce(robust)使用vce(robust)参数后，回归结果中的系数和标准误都是异方差稳健的，并且t值和p值也已经经过了调整。
总结：通过Breusch-Pagan-Godfrey检验或White检验可以检验异方差问题，如果存在异方差问题，可以使用异方差稳健标准误或异方差稳健回归来解决。
在使用robust命令时，不需要进行任何假设检验，因为参数已经考虑了异方差问题。
异方差性的检验及处理方法
异方差性的检验及处理方法异方差性是指随着自变量变化，因变量的方差不保持恒定，即方差存在不均匀的变化趋势。
在统计分析中，如果忽视了异方差性，可能会导致误差的不准确估计，从而影响对因变量的显著性检验和参数估计结果的准确性。
为了避免异方差性给统计分析带来的影响，需要进行异方差性的检验和处理。
下面将介绍几种常用的异方差性检验及处理方法。
一、异方差性的检验方法：1.绘制残差图：绘制因变量的残差（观测值与拟合值之差）与自变量的散点图，观察残差是否随着自变量的变化而存在明显的模式。
如果残差图呈现出锥形或漏斗形状，则表明存在异方差性。
2.帕金森检验：帕金森检验是一种常用的检验异方差性的方法。
该方法的原理是通过对残差进行变换，判断变换后的残差是否与自变量相关。
3. 布罗斯-佩根检验（Breusch-Pagan test）：布罗斯-佩根检验是一种常用的检验异方差性的方法。
该方法的原理是通过计算残差与自变量的相关系数，进而判断是否存在异方差性。
4. 品尼曼检验（Leve ne’s test）：品尼曼检验是一种非参数的检验方法，可以用于检验不同组别的方差是否存在显著差异。
二、异方差性的处理方法：1.变量转换：通过对因变量和自变量进行变换，可以使数据满足异方差性的假设。
比如可以对因变量进行对数转换或平方根转换，对自变量进行标准化处理等。
2.使用加权最小二乘法（WLS）：加权最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权，使得残差的方差与自变量无关。
3.使用广义最小二乘法（GLS）：广义最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权，使得残差的方差可以通过自变量的一个线性组合来估计。
4.进行异方差性的鲁棒估计：鲁棒估计是一种对异常值和异方差性具有较好鲁棒性的估计方法。
通过使用鲁棒估计，可以减少异方差性对参数估计的影响。
综上所述，异方差性是统计分析中需要重视的问题。
logit异方差
Logit模型中的异方差问题通常指的是误差项的方差不是常数，而是随着自变量的变化而变化。
在Logit模型中，异方差性是一个需要注意的问题，因为它可能违反了模型的基本假设，从而影响参数估计的准确性和统计推断的有效性。
首先，需要明确的是，Logit模型假设因变量的条件分布是Logistic分布，并且误差项独立于自变量。
如果存在异方差，那么这个假设可能不成立。
在这种情况下，可以考虑以下几种方法来处理异方差问题：
1. 模型诊断：使用统计检验来检测是否存在异方差。
虽然Logit模型没有类似OLS模型中的`hetprob`命令来进行异方差检验，但可以使用其他统计软件或编写自定义程序来进行类似的检验。
2. 变换数据：有时候对数据进行适当的变换可以减轻异方差的影响。
例如，可以尝试对自变量进行变换，或者对因变量的概率进行Logit变换。
3. 加权最小二乘法（WLS）：如果检测到异方差，可以使用加权最小二乘法（WLS）来估计模型参数。
这种方法通过给不同的观测赋予不同的权重来调整异方差的影响。
4. 稳健标准误：在存在异方差的情况下，可以使用稳健标准误来进行参数估计。
稳健标准误不依赖于误差分布的具体形式，因此可以在异方差存在的情况下提供更准确的标准误估计。
5. 模拟方法：使用蒙特卡洛模拟等方法来估计模型参数和标准误，这些方法不依赖于误差分布的具体形式，因此可以在一定程度上解决异方差问题。
6. 选择其他模型：如果Logit模型不适用，可以考虑使用其他更适合数据的模型，如Probit模型或者其他非线性模型。
异方差性的解决方法.
* i
由于在极小化过程中对通常意义得残差平 方加上了权数ω i，所以称为加权最小二乘法 （Weighted Least Square—WLS ）。 ω i有两个作用:一是权重，二是为了消除 异方差。 注意权数的变化趋势应与异方差的变化趋 势相反，通常将ω i直接取成1/σ i2 。
模型变换法的实质就是WLS 例如，对于模型 yi=a+bxi+ε i 如果σ i2 =D(ε i)＝λ xi2，则模型变换成
③选定Weighted LS方法，在权数变量栏中输入权 数变量，点击OK返回； ④点击OK，采用WLS方法估计模型。 （4）对估计后 q1模型，再使用White检验判断是否 消除了异方差性。
4.4.3
模型的对数变换
如果在模型yt=b0+b1xt+ut中，分别用lnyt、lnxt 取代，对对数模型 lnyt=b0+b1lnxt+ut 进行回归通常可以降低异方差性的影响。 其原因在于（1）通过对数变换将两个数值之 间原来10倍的差异缩小到只有2.3倍左右的差 异。（2）经过对数变换后的线性模型，其残 差et表示为相对误差，而相对误差往往具有较 小的差异。
* i
y ax bx
* 2i
* i
i 1 此时 D ( ) D ( ) 2 D ( i ) 1 i i 使用OLS估计模型，应使得： yi 1 ˆ xi *2 * * 2 ˆ b ) ˆi ) ( a ei ( yi y i i i 1 ˆx ) 2 min ˆ b 2 ( yi a i i 1 ˆ ˆ i yi (a ˆ bxi ) 若记: ei yi y 并设:i 2 i 2 则以上估计过程是使得: i ei min
由于在极小化过程中对通常意义得残差平 方加上了权数ω i，所以称为加权最小二乘法 （Weighted Least Square—WLS ）。 ω i有两个作用:一是权重，二是为了消除 异方差。 注意权数的变化趋势应与异方差的变化趋 势相反，通常将ω i直接取成1/σ i2 。
模型变换法的实质就是WLS 例如，对于模型 yi=a+bxi+ε i 如果σ i2 =D(ε i)＝λ xi2，则模型变换成
③选定Weighted LS方法，在权数变量栏中输入权 数变量，点击OK返回； ④点击OK，采用WLS方法估计模型。 （4）对估计后 q1模型，再使用White检验判断是否 消除了异方差性。
4.4.3
模型的对数变换
如果在模型yt=b0+b1xt+ut中，分别用lnyt、lnxt 取代，对对数模型 lnyt=b0+b1lnxt+ut 进行回归通常可以降低异方差性的影响。 其原因在于（1）通过对数变换将两个数值之 间原来10倍的差异缩小到只有2.3倍左右的差 异。（2）经过对数变换后的线性模型，其残 差et表示为相对误差，而相对误差往往具有较 小的差异。
* i
y ax bx
* 2i
* i
i 1 此时 D ( ) D ( ) 2 D ( i ) 1 i i 使用OLS估计模型，应使得： yi 1 ˆ xi *2 * * 2 ˆ b ) ˆi ) ( a ei ( yi y i i i 1 ˆx ) 2 min ˆ b 2 ( yi a i i 1 ˆ ˆ i yi (a ˆ bxi ) 若记: ei yi y 并设:i 2 i 2 则以上估计过程是使得: i ei min
异方差性的检验及处理方法
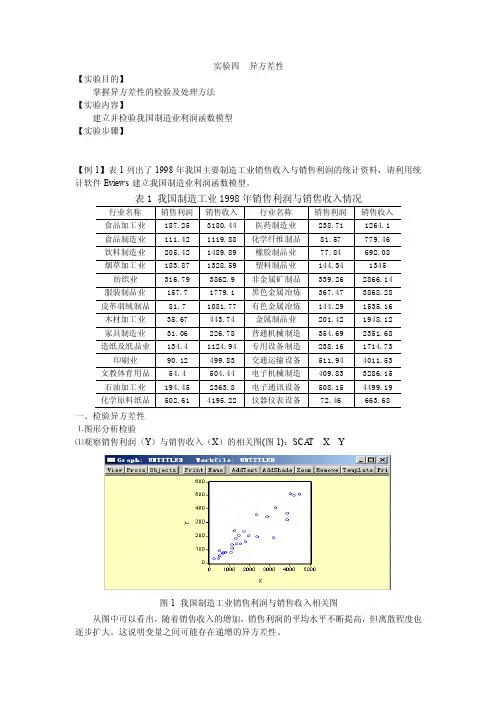
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润（Y）与销售收入（X）的相关图(图1)：SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察）。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）⑵利用样本1建立回归模型1（回归结果如图3），其残差平方和为2579.587。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2（回归结果如图4），其残差平方和为63769.67。
SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝63769.67/2579.59=24.72，21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性⒊White 检验⑴建立回归模型：LS Y C X ，回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
第四节异方差性的补救措施
F 5.0762 F0.05 (6, 6) 4.28 拒绝原假设，表明模型存在异方差。
38
（三）White检验
存在异方差
39
四、异方差的修正
加权最小二乘法（WLS）
分别选用权重:
w1
1 Xi
, w2
1 Xi
, w3
1 X 1.5
i
, w4
1 Xi2
经估计检验发现用权数w2可以消除异方差性。
◆对数变换能使变量取值的尺度缩小。 ◆经过对数变换后的模型，其残差表示相对误差，往往比
绝对误差有较小的差异。
注意：取对数后变量的经济意义。
34
第五节 案例分析
一、问题的提出和模型设定
为了给制定医疗机构的规划提供依据，分析比 较医疗机构与人口数量的关系，建立卫生医疗机 构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束， 则理论模型设定为：
经检验ui存在异方差，且已知方差表达式为
var(ui )
2 i
2
f
(Xi)
用 f (Xi ) 除以模型的两端得：
Yi =
f Xi
f
β1
X
i
+
β2
Xi +
f Xi
ui
f Xi
记 Yi* 则有：
Yi f (Xi)
;
X
* i
Xi f (Xi)
; 1*
Yi*
1*
2
X
* i
vi
1
f (Xi)
; vi
ui f (Xi)
1
2 i
Yi 1* 2* X i
2
1
2 f Xi
第五章第四节 异方差的解决方法
（5）权数的选择（**）
• 一般地，Wi=1/2i。问题在于：2i一般是未知的 • 关键：找出ui随着Xi的变化而变化的规律，对异方差
Var(ui)= 2i = 2 f( Xi )（ i=1,2,…,n）的具体形式作出 合理假设。
• 怎样才能提出合理的假设呢？ （1）通过对具体经济问题的经验分析，或 （2）考察OLS的ei2与Xi的关系，或 （3）通过White等检验的结果提供的信息 • 粗略做法： Wi =1/|ei|或1/ ei2 ，ei是OLS估计的残差 • 所以，利用WLS的思路是：寻找合适的“权数”，
4.WLS法在eviews中的实现
1.创建文件：File/New/Workfile/输入数据频率/Ok 2.输入数据：在主菜单，点quick / empty group/输入变量
名称和数值/ 3.产生新序列：在eviews栏，点quick/generate series/输
入w=1/sqr(x)，点ok(假设w=1/sqr(x) 4.作回归：在eviews栏，点quick/ estimate equation/键入
变量和常数[如y c x]，同时点右下方的option，选择 Weighted LS/TLS，键入w，点ok
同质性 权数序列名
二、对原模型变换的方法
1、模型变换法的定义
模型变换法是对存在异方差的总体回归模型作适当的代数变换，使之成为满足同方 差假定的模型 , 进而运用OLS方法估计参数。
2、模型变换法的关键是： 通过对具体经济问题的经验分析，事先对异方差
往往有较小的差异。
利用EViews对模型进行对数变换
例 ln Yi 1 2 ln Xi ui 在eviews栏，点quick/generate series/输入 LY=LOG（Y） 在eviews栏，点quick/generate series/输入 LX=LOG（X）
消除异方差的方法
消除异方差的方法异方差是啥玩意儿？简单来说，就是数据中的误差项不满足同方差性。
这可咋整呢？别慌！有办法消除异方差。
一种方法是加权最小二乘法。
嘿，就像给不同的数据点分配不同的“权重”。
步骤呢，先判断是否存在异方差，可以通过残差图等方法。
如果确定有，那就计算权重。
然后用加权后的数据进行最小二乘法估计。
注意啦，权重的选择可不能瞎选，得根据具体情况来。
这就好比做菜放盐，多了咸，少了淡。
那安全性和稳定性咋样呢？一般来说，只要方法得当，还是挺靠谱的。
不会像走钢丝那么惊险，放心大胆地用。
这种方法的应用场景可多啦！比如在经济学、统计学等领域。
优势嘛，能提高估计的准确性和有效性。
想象一下，这就像给你的眼睛戴上了一副度数合适的眼镜，看东西更清楚了。
举个实际案例呗！比如说研究收入和消费的关系，发现不同收入水平的人消费的差异很大，存在异方差。
用加权最小二乘法处理后，模型的拟合效果明显提升。
哇塞，这效果杠杠的！还有一种方法是对数变换法。
把数据进行对数变换，有时候就能消除异方差。
这就像给数据来个“魔法变身”。
步骤是先对数据取对数，然后再进行分析。
注意哦，不是所有数据都适合这种方法，得先看看数据的特点。
安全性方面呢，通常比较安全，不会出啥大乱子。
稳定性也还不错。
它的应用场景也不少呢！在金融、工程等领域都能派上用场。
优势就是简单易行，不需要太复杂的计算。
就像骑自行车，轻松又自在。
比如说在股票市场分析中，股价和成交量可能存在异方差。
通过对数变换，能让数据更稳定，分析起来更顺手。
嘿嘿，是不是很厉害？总之，消除异方差的方法有很多，要根据具体情况选择合适的方法。
只要用心去做，就能让数据变得更听话，分析结果更可靠。
相信自己，一定能搞定异方差这个小麻烦！。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
广义最小二乘估计量为
~ ( X *' X * )1 X *'Y *
(5.4.20)
将(5.4.17)代入(5.4.20)
~ [(PX )(PX )]1(PX )(PY)
( X PPX )1 X PPY ( X 1 X )1 X 1Y
(5.4.20)′
(5.4.20)(或(5.4.20)′)称为广义最小二乘估计式。这种
ui ) V (ui ) k 2 f (xi ) k 2 f (xi ) f (xi ) f (xi )
因此，对模型(5.4.5)应用OLS法，即可得出参数 α、β的最佳线性无偏估计量，问题得以解决。
例5.4.1
设模型(5.4.1)中ui的异方差结构为
2uiຫໍສະໝຸດ k2xi2(这是一种最常见的异方差结构)，求α、β的最佳
将原模型(5.4.11)进行适当变换，变为模型(5.4.18)，
然后对新模型(5.4.18)应用普通最小二乘法，求得参数
估计量，称作对原模型的广义最小二乘法，记作GLS。
当Ω = In时， ( X ' X )1 X 'Y ˆ
(5.4.21)
此时广义最小二乘法就是普通最小二乘法。
参数的协方差矩阵
, x*2i
ui f (xi)
xi f (xi)
(5.4.3)
,u*i
ui (5.4.4)
f (xi)
则模型(5.4.3)变为
y*i x1*i x*2i u*i
(5.4.5)
(5.4.5)中的参数α和β即原模型中的参数，但是随
机项 ui* 已经没有异方差性了。因为：
V (ui*) V (
2
i
f (xi)
(
yi f (xi)
f
1 (xi
)
(
y
i
ˆ
ˆ
xi )2
ˆ
f (xi)
ˆ )2
f (xi)
(5.4.10)
最小。显然，能使(5.4.10)达到最小的 ˆ 、ˆ 也一定 能使(5.4.9)式达到最小，因为二者只差一个常数因子。 即两种方法得到的结果相同。两种方法实质上是一回 事。对原模型进行变换的方法实际上是加权最小二乘 法当 1 1 时的特例，也可以看作是加权最小二乘法
1 '1
n k 1
(5.4.23)
其中ε为广义最小二乘估计量所对应的模型(5.4.11) 的样本残差。
四、广义最小二乘法的应用之一 —— 异方差问题的处理
设模型
Y X U
(5.4.24)
§5.4 异方差性问题的解决方法 一、对原模型进行变换
设原模型为
yi xi ui
(5.4.1)
其中ui具有异方差性(其余假定都满足)。假定现在已知
V
(ui
)
2
ui
k 2 f (xi )
(5.4.2)
其中k2为常数。现在的问题是经典假定遭到了破坏的
情况下，如何求出参数α、β的最佳线性无偏估计量?
解决这个问题的基本想法是对原模型(5.4.1)作适当
的变换，使变换后的随机项不再具有异方差，从而
可用OLS法求出参数的最佳线性无偏估计量。
用 f (xi ) 去除(5.4.1)式两端，则得到新的模型：
yi f (xi)
f (xi)
f(
x
i
)
x
i
记
y*i
yi f (xi)
, x1*i
1 f (xi)
线性无偏估计量。
在本例中 f (xi) xi2 ， f (xi) xi ，用 xi 去除(5.4.1) 式各项，得
改写成
yi ui
xi xi
xi
其中
yi* xi* ui*
y*i
yi xi
,
x*i
1 xi
, u*i ui xi
由于变换后的模型中的随机项
u
* i
已没有异方差，
(5.4.8)
将(5.4.8)代入(5.4.7)得加权最小二乘法，要求
2 i
2 ui
k2
1 f(
xi)
(
y
i
ˆ
ˆ
xi )2
达到最小。
现在对原模型(5.4.1)作变换：
(5.4.9)
yi f (xi)
f (xi)
f (xi) xi
ui f (xi)
(5.4.3)
对(5.4.3)应用普通最小二乘法，要求残差平方和：
PY PX PU
令
Y * PY X * PX U * PU
(5.4.16) (5.4.17)
则(5.4.16)变为
Y* X * U*
(5.4.18)
此时
E(U
*U
*
'
)
E(PUU
P)
PE(UU
)P
2 u
I
n
(5.4.19)
可见，变换后的模型(5.4.18)，已满足全部基本假定，
可以对模型(5.4.18)应用普通最小二乘法，求得β的
nn
n1 n2
1n
2n
nn
(5.4.13)
其它基本假定不变，称之为广义线性模型。
若将Ω换成In，则模型(5.4.11)就变成一般古典线性模型。 由于Ω为正定对称矩阵，必存在一个(n×n)阶非奇异矩
阵P，使得
PP ' In
(5.4.14)
且有
1 P ' P
(5.4.15)
利用矩阵P对原模型进行变换，用P左乘(5.4.11)得，
V
COV
(~)
2 u
(X
*
X
* ) 1
u2[(PX )(PX ) ]1
2 u
(
X
1
X
) 1
(5.4.22)
ˆ u 2
*' *
n k 1
n
1 k
(Y * 1
X
*
)' (Y *
X
*
)
1 (PY PX )'(PY PX )
n k 1
1 (Y X )' 1(Y X )
n k 1
k2 的直接应用。
三、广义最小二乘法 ( GLS ) 广义最小二乘法是处理广义线性模型的一种估计方法。
广义线性模型是指线性模型
Y X U
(5.4.11)
并且有
E(U ) 0
E
(UU
')
u
2
(5.4.12)
其中 u2为未知常数，Ω是一个已知的n×n阶正定
对称矩阵：
11 12 21 22
V (ui )
2 ui
作为εi2的权数是合理的。
现在我们可以用权数将普通最小二乘法修正为： 使加权残差平方和
2 i
2 ui
1
2 ui
(
y
i
ˆ
ˆ
xi )2
(5.4.7)
达到最小。这就是加权最小二乘法。
下面我们说明，这种加权最小二乘法同样可以消除
异方差性的影响。
设异方差是xi的函数
2 ui
k2 f (xi )
应用OLS法得α和β的最佳线性无偏估计量：
ˆ
xi* yi* xi*2
ˆ y* ˆ x *
二、加权最小二乘法(WLS)
在OLS法中，其基本原则是使残差平方和
2 i
(
y
i
ˆ
ˆ
x
2
i)
(5.4.6)
达到最小，这是对满足经典回归假定而言，也就
是在等方差的情况下进行的。当随机项具有异方差
时，用
1 1