俄罗斯方块中的数学知识 PPT
- 格式:pptx
- 大小:7.37 MB
- 文档页数:10

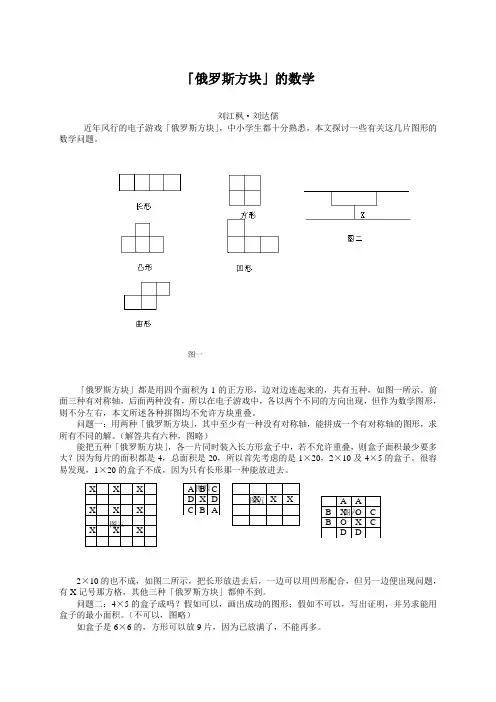

俄罗斯方块平移和旋转数学题
俄罗斯方块是一种游戏,由七种形状不同的方块组成。
这七种方块分别是:I字型、J字型、L字型、O字型、S字型、T字型和Z字型。
在俄罗斯方块游戏中,玩家需要通过平移和旋
转方块来使其在游戏区域内堆叠成完整的一行或多行,当一行或多行被填满后,这些行将被消除,玩家可以得到分数。
平移:俄罗斯方块可以向左或向右进行平移,每次平移可以将方块在水平方向上移动一个单位。
设方块当前位置为(x, y),
则向左平移后的新位置为(x-1, y),向右平移后的新位置为(x+1, y)。
旋转:俄罗斯方块可以进行顺时针或逆时针旋转。
设方块当前位置为(x, y),则设旋转中心为(cx, cy),顺时针旋转后的新位
置为(x', y'),可以通过以下公式计算得出:
x' = cx + (y - cy)
y' = cy - (x - cx)
逆时针旋转后的新位置为:
x' = cx - (y - cy)
y' = cy + (x - cx)
需要注意的是,旋转中心(cx, cy)的选择需要注意不同方块的
形状和旋转要求。
以上就是俄罗斯方块平移和旋转的数学原理和操作方式。
在实
际游戏中,玩家可以根据方块的形状和位置来进行平移和旋转,以达到堆叠成完整行的目标。

【高中数学】“俄罗斯方块”背后的数学故事1984年的时候,当时还名不见经传的阿列克谢帕基特诺夫(alexeypajitnov)只是苏联科学院计算机中心的一位普通的工程师。
他热衷于开发电脑游戏,不过这些游戏卖得都不好。
那年夏天,他突然又想到了一个新点子――让不同形状的积木落进一个矩形的玻璃容器里,在容器底部堆叠起来,使之排列成完整的一行或多行。
在两位同伴的协助下,他很快编写好了这个游戏。
尽管他预感到这项运动可能会着火,但他对结果感到震惊:这项运动很快在莫斯科流行起来,很快在全世界流行起来。
在接下来的27年里,这款游戏被移植到几乎所有的计算机系统和游戏平台上。
许多MP3、MP4、手机、电视,甚至示波器也随游戏而来。
它还衍生了其他类型的游戏方法,极大地丰富了解谜游戏的类型。
这个大家都知道的经典游戏后来被命名为俄罗斯方块。
俄罗斯方块的小知识你对俄罗斯方块了解多少?你知道俄罗斯方块游戏场的大小吗?你知道每个广场的名字吗?俄罗斯方块的游戏场地是一个宽为10,高为20的矩形。
游戏里共有7种方块,根据它们的形状分别命名为i,j,l,o,s,t,z。
玩家需要控制不断下落的方块填放到合适的位置,被填满的行将自动消除。
视局面的不同,玩家一次可消除1行至4行不等,这在游戏里分别叫做single、double、triple和tetris。
一次性消除的行数越多,得分也就越高。
随着被消除的总行数的增加,方块下落速度会越来越快。
一旦某个方块放置后超出了场地高度,游戏便自动结束。
俄罗斯方块背后的数学问题到如今俄罗斯方块已经诞生27年了。
在这27年里,俄罗斯方块不但让几代玩家为之疯狂,也让不少数学家沉迷于其中。
俄罗斯方块提出的第一个数学问题是,如果玩家的技术足够高,游戏是否永远不会结束?1988年,约翰?约翰·布尔祖斯托斯基(John Brzustowski)的一篇论文指出,如果“s”和“Z”块以适当的间隔交替出现,那么游戏区域将不可避免地出现越来越多无法消除的线条,最终导致游戏结束。

俄罗斯方块最详解(C语言实现)俄罗斯方块最详解做每一件事前,都会有一个粗略的构想。
编程更应该这样,现在先说一些大的、粗略的东西。
******************************************************************************* **************************************************************************************** *********目录:●屏幕的划分●图形显示●三种坐标。
绝对坐标、相对坐标、左上角坐标●方块的构造●动画效果●键盘控制●判断方块碰撞●消行●变形●关于菜单的制作●附录(完整的源程序)******************************************************************************* **************************************************************************************** *********1、屏幕的划分将整个屏幕划分成四部分:a、一个没盖的杯子;b、一个不断下落4*4数组的盒子;c、一个给预览下一个方块4*4数组的盒子;d、提示信息。
由于提示信息比较简单,这里只讨论前三样。
没盖的杯子:即平时说玩这款游戏时,下落方块不可超出的那个边界,下落的方块从这个“杯口”的上方往下下落,方块只在“杯子”里移动、变形、停止。
游戏空间指的是整个游戏主要的界面(呵呵,其实就是所说的“杯子”)。
实际上是一个宽10格子、高20格子的游戏板。
用一个全局数组GameSpace[22][12]表示。
表示的时候:GameSpace[x][y]为1时表示游戏板上(x,y)这个位置上已经有方块占着了,GameSpace[x][y]为0表示游戏板上这位置还空着。


俄罗斯方块算法以及原理
俄罗斯方块游戏是一种经典的游戏,由苏联工程师阿列克谢·帕基特诺夫于1984年发明。
本文将介绍俄罗斯方块游戏的算法和原理。
算法:
俄罗斯方块游戏的核心算法是形状旋转和移动。
俄罗斯方块由七种不同的形状组成,每个形状可以旋转四次,以使其适应特定的空间。
这些形状是由方块组成的,每个方块都有一个颜色。
游戏按照随机顺序生成这些形状,并将它们放在游戏区域的顶部。
玩家控制形状在游戏区域内移动和旋转,以使形状下落并适应游戏区域中的空间。
当一行被填满时,它将立即消失并获得积分。
游戏结束当游戏区域的空间被占满。
原理:
俄罗斯方块游戏的原理是基于图形学和物理学的。
游戏区域是由一个N*M的矩形组成,其上有一个由方块组成的初始形状。
游戏区域的边缘是一个虚拟的围墙,当形状碰到围墙时,它将停止并被固定在当前位置。
当形状下落时,它受到重力和空气阻力的影响。
游戏采用迭代的方式来模拟形状的运动,每一帧都会更新形状的位置和状态,同时检测碰撞和消除行的条件。
总结:
俄罗斯方块游戏的算法和原理是基于图形学和物理学的,其核心算法是形状旋转和移动,游戏区域的边缘是一个虚拟的围墙,当形状碰到围墙时,它将停止并被固定在当前位置。
游戏的迭代方式模拟形状的运动,同时检测碰撞和消除行的条件。
这些算法和原理为俄罗斯方块游戏的可玩性和可扩展性打下了基础。
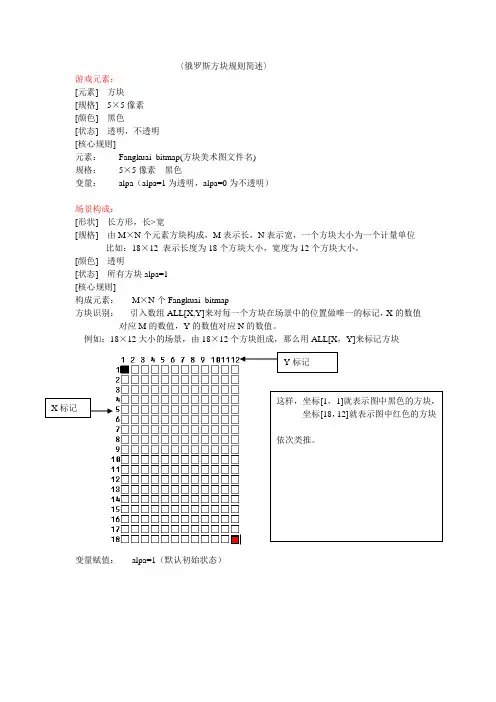
〈俄罗斯方块规则简述〉 游戏元素: [元素] 方块[规格] 5×5像素 [颜色] 黑色[状态] 透明,不透明 [核心规则]元素: Fangkuai_bitmap(方块美术图文件名) 规格: 5×5像素 黑色变量: alpa (alpa=1为透明,alpa=0为不透明)场景构成:[形状] 长方形,长>宽[规格] 由M ×N 个元素方块构成,M 表示长,N 表示宽,一个方块大小为一个计量单位 比如:18×12 表示长度为18个方块大小,宽度为12个方块大小。
[颜色] 透明[状态] 所有方块alpa=1 [核心规则]构成元素: M ×N 个Fangkuai_bitmap 方块识别: 引入数组ALL[X,Y]来对每一个方块在场景中的位置做唯一的标记,X 的数值对应M 的数值,Y 的数值对应N 的数值。
例如:18×12大小的场景,由18×12个方块组成,那么用ALL[X ,Y]来标记方块变量赋值: alpa=1(默认初始状态)X 标记Y 标记这样,坐标[1,1]就表示图中黑色的方块, 坐标[18,12]就表示图中红色的方块依次类推。
积木生成:[元素] 方块[规格] 由4个方块按照一定规则组合而成,如图:共计19件[颜色]黑色[状态]不透明[核心规则]积木是通过场景中以下坐标标记的方块的alpa值来生成的:[1,Y\2-1] [1,Y\2] [1,Y\2+1][2,Y\2-1] [2,Y\2] [2,Y\2+1][3,Y\2-1] [3,Y\2] [3,Y\2+1]生成积木的时候,更改相应的方块变量值,其变量alpa=0以下坐标标记的方块为需要更改alpa值的方块:(参考场景构成的[方块识别] )积木代号:A_1积木代号:A_2积木代号:B_1积木代号:B_2积木代号:C_1积木代号:C_2积木代号:C _3积木代号:C_4积木代号:D_1积木代号:D_2积木代号:D_3积木代号:D_4积木代号:E_1积木代号:F_1积木代号:F_2积木代号:G_1积木代号:G_2积木代号:G_3积木代号:G_4碰撞检测规则:[碰撞规则](在方块下落之前,我们要先进行碰撞检测。


俄罗斯方块数学原理
哇塞,你知道吗,俄罗斯方块里居然隐藏着神奇的数学原理呢!就像搭积木一样,每一块方块的掉落和组合都有着特别的规律。
比如说,当那些不同形状的方块一个接一个落下来时,这不就像我们生活中一项一项的任务接踵而至嘛!你得想办法把它们合理地安排摆放,不然就会堆得乱七八糟。
这和我们规划时间是不是很像呀?
再看看游戏里消除一行行方块的时候,哎呀,那感觉简直太棒啦!就好像我们解决了一个又一个难题,满满的成就感。
这不就是数学中的排列组合吗?不同形状的方块有着不同的组合方式,我们要找到最优解,把它们完美地融合在一起。
我和朋友一起玩俄罗斯方块的时候,那可热闹啦!我喊着:“哎呀,这个方块怎么这么难缠啊!”朋友笑着回应:“哈哈,你得动动脑筋呀!”我们在游戏的过程中互相竞争,又互相学习。
这不就好比我们在学习数学的道路上,和同学们一起探讨、一起进步嘛!
你想想看,每次方块的掉落和旋转,不正是一次次的尝试和探索吗?就如同我们在数学中尝试用不同的方法去解题一样。
俄罗斯方块就像是一个小
小的数学世界,充满了挑战和乐趣。
而且,它还能锻炼我们的反应速度和空间思维呢!
所以啊,俄罗斯方块可不只是一个简单的游戏,它背后蕴含的数学原理真的超级有趣!这就是我的观点,俄罗斯方块真的和数学有着千丝万缕的联系呀!。

14你知道吗?俄罗斯方块这种拼图游戏中蕴含着数学知识。
俄罗斯方块游戏中共有7种不同形状的方块不断随机下落,玩家通过自行变换随机掉下来的方块形状,将之填放到适当的位置,被填满的行将自动消除。
玩家一次可消除1行至4行不等。
随着被消除的总行数不断增加,方块下落的速度越来越快,一旦某个方块放置后超出了原规定矩形的高度,游戏便自动结束。
在游戏过程中,一次消去1行得100分,消去2行得300分,消去3行得600分,消去4行得1000分,由此可知,消1行的得分与消掉行数的比值是100:1,消2行的得分与消掉行数的比值是150:1,消3行的得分与消掉行数的比值是200:1,消4行的得分与消掉行数的比值是250:1,显然这一比值是递增的,依次增值的数额为50。
我们再分析消去不同行数所得分数的规律,发现300-100=200,600-300=300,1000-600=400,即相邻两个数的差也呈递增形式,依次增值的数额是100。
这两条规律都说明把方块一次聚集到2行、3行、4行再消掉的话,得分会比一行行地消去得到的分数高得多。
如果玩家的技术水平高超,那么游戏是否永远不会结束?答案是否定的。
当S 形方块和Z 形方块以适当的间隔交替出现时,游戏区域将不可避免地出现越来越多无法消去的行,最终导致游戏结束。
虽然这种情况发生的概率极小,但仍然是有可能的。
游戏中用到的7种方块的总面积为28格,若每块只能用1次且允许翻转,能否用这7个不同形状的方块拼出一个完整的矩形呢?答案也是否定的。
原因很简单,利用染色策略,将方格按黑白相间进行染色,会发现每种方块总是占据两个黑色格子和两个白色格子,只有T 形方块所占的黑白格子个数始终不等,所以7个方块所占据的黑白格子总数也不相等,但在一个规定的矩形区域内黑白格子数目是相等的,因此,它不能被这7个方块完全覆盖住,用7种方块拼成一个完整的矩形是不可能的。
. All Rights Reserved.。
“俄罗斯方块”之数学辨析作者:林革来源:《初中生世界·七年级》2014年第10期说起“俄罗斯方块”这个入门级游戏,也许如今许多网游迷并不熟悉,但对于年龄稍长的或骨灰级的玩家而言,当初迷恋这个游戏的程度,用目不转睛和废寝忘食来形容亦不为过,由此可见“俄罗斯方块”面世后的魅力和诱惑.这种结果甚至出乎游戏制作者——电脑工程师阿列克谢·帕基特诺夫的预料,因为他之前开发的电脑小游戏,无一例外遭受冷遇.1984年夏天他又琢磨起“俄罗斯方块”,但完成制作后仍缺乏信心.事实令他瞠目结舌——“俄罗斯方块”在莫斯科迅速流行,并在此后的30年里风靡全球.它被移植到了几乎所有的电脑系统和游戏平台上,包括MP3、MP4、手机、电视,最近甚至有人把它组装在了T恤上.借助这些日益普及的传播工具,“俄罗斯方块”很快成为无人不知无人不玩的经典游戏.尽管这个曾广为流传的游戏现在已淡出玩家视线,但细细辨析并研究其中蕴含的一些数据规律,以及相关的数学问题,仍具追思意味和现实意义.俄罗斯方块的游戏空间是一个宽为10、高为20的矩形.游戏里共有7种方块(如图)不断随机下落,根据它们的形状分别命名为I, J, L, O, S, T, Z.玩家需要调整变换方块使之填放到合适位置,被填满的1行至4行将自动消除.一次性消除的行数越多,得分就越高.在游戏过程中,一次消去1行得100分…①,一次消去2行得300分…②,一次消去3行得600分…③,一次消去4行得1000分…④,从这些数据中可以发现,在各种情况下,每行消去后的得分并不是恒定不变的,换句话说,一次的得分与消掉的行数的比有所变化.①式中的得分与消掉的行数的比是100∶1;②式中的得分与消掉的行数的比是150∶1;③式中的得分与消掉的行数的比是200∶1;④式中的得分与消掉的行数的比是250∶1.显然它们的比值是呈递增形式的,而且依次增值的数额是50.这是从单行得分数上去分析的,如果我们从总得分上来分析,可发现100、300、600、1000的变化规律是300-100=200,600-300=300,1000-600=400,相邻两个数间的差额也是呈递增形式的,而且依次增值的数额是100.这两条规律都说明同一个事实:如果一次聚积到2行、3行,甚至是4行消掉的话,那得分会比一行一行消去的分数要多得多.此游戏就是鼓励玩家尽可能拼成完整的几行一块儿消去,这样积分增加的速度会大大提高.这就是老玩家经常大比分获胜的诀窍所在.而另一个令人沮丧的事实是:随着被消除总行数的增加,方块下落速度会越来越快.一旦某个方块放置后超出了场地高度界限,游戏便告结束.无论新老玩家,有多少窍门或熟练手法,到最后都无法避免手忙脚乱左右不能顾及的局面,只能在摇头叹息中从头再来.由此,“俄罗斯方块”引出的第一个数学问题是:如果玩家的技术足够高,游戏是否永远也不会结束?1988年,约翰?布鲁托斯基的一篇论文指出,若“S”型和“Z”型方块以适当的间隔交替出现时,游戏区域中将不可避免地出现越来越多无法消去的行,最终导致游戏结束.虽然这种情况发生的概率并不高,但考虑到问题的假设——游戏的无限操作,这样的情形肯定会出现,因此理论上问题的答案是否定的.如果说以上解释略显模糊,那么下面问题的答案就非常确定.“俄罗斯方块”有7种方块,每种方块都由4个小方格组成,即它们的总面积为28.如果每块只能用一次,并允许翻转,请问你能用它们拼出4×7的长方形(如图1)吗?对这个问题的巧妙解答可借助染色策略.即将图1的每个小方格用黑白两色相间染色(如图2),黑白小方格的数量相同,各14个,这就表明,七种俄罗斯方块如果能够拼成图2,那么它们盖住的黑白方格数必须相等.而对于游戏中7种俄罗斯方块,稍加试验可知:I, J,L, O, S, Z无论如何摆放,都各盖住两个黑色小方格与两个白色小方格,但“T”型方块无论如何摆放,都一定盖住一个黑色小方格和三个白色小方格或一个白色小方格和三个黑色小方格.正由于“T”型方块所占的黑白格子个数始终不等,才导致这7种俄罗斯方块盖住的小方格与白色小方格的数量不可能相等,这就说明用7种俄罗斯方块拼成图(1)是不可能的.不难理解的是,7个俄罗斯方块可以拼成图3,因为特殊的“T”型方块对应放在了特殊的位置——突出的一块.如此一来,这7种俄罗斯方块恰好能构成一个平面镶嵌(如果一组几何图形能够既无重叠又无空缺地填满整个平面,我们就把它称作一种平面镶嵌).也正因为此,许多家装公司的设计师别出心裁,把墙砖或地砖做成了图3平铺,巧妙运用“俄罗斯方块”给居家生活带来几分创意(图4).类似的创意还体现在用“俄罗斯方块”构成的各种趣味拼图.比如:如何把6个“L”形状的方块摆放在一起,使得每个“L”恰好都和另外三个“L”相邻?(答案如图5);怎样用奇数个“L”摆成一个轴对称图形?(如图6).这些看起来极易上手,但实际操作起来却困难重重的拼图,充分体现了数学思维与空间想象的巧妙新颖.(作者单位:江苏省扬州职业大学师范学院)。