重力坝应力分析例题

1、计算依据：《混凝土重力坝设计规范》（DL5108-1999）2、计算工况：按正常使用极限状态设计，考虑下列两种作用效应组合：a 、短期组合：持久状况或短暂状况下，可变作用的短期效应永久作用效应的组合。

b 、长期组合：持久状况下，可变作用的短期效应永久作用效应的组合。

3、计算公式：a 、短期组合采用下列公式：b 、长期组合采用下列公式：式中： C 1、C 2—结构的功能限值，Ss （·）、S l （·）—作用效应的短期组合、长期组合时的效应函数，γd3、γd4—正常使用极限状态短期组合、长期组合时的结构系数，ρ—可变作用标准值的长期组合系数，规范取ρ=1G K —永久作用标准值，Q K —可变作用标准值，f k —材料性能的标准值，a k —几何参数的标准值（可作为定值处理）4、计算计算中考虑将正常水位作为长期组合，设计水位和校核水位作为短期组合，计算中不考虑扬压力（因为上游面设置了C20混凝土防渗墙）。

因坝体横剖面有两个折点，因此计算分两个截面进行,分别为1078.770和1066.000高程。

计算内容为各截面在各种组合下上、下面的应力（拉应力和压应力）荷载水平方向以向右为正，垂直方向以向下为正，力矩以顺时针方向为正。

4.1 1078.770m 截面4.1.1荷载计算(1).永久作用标准值（自重）：坝顶宽度 3.000m坝顶高程1083.452则截面高4.682m ，截面以上面积S=14.046m 2坝体材料容重为γ= 2.300t/m 3所以坝体自重G K 为：32.3058t 自重到截面中心的力臂为：0.000m 自重到截面中心的力距为：0t·m (2).可变作用标准值：正常水位1081.500水压力=0.5·γ·H 2=3.726t 水压力到截面中心力臂为：0.91m 水压力到截面中心力距为： 3.391t·m坝体应力计算书()310/,,,d K K K K S C a f Q G S g g £()420/,,,d K K K K l C a f Q G S g r g £设计水位1082.300水压力=0.5·γ·H 2=6.230t 水压力到截面中心力臂为：1.177m 水压力到截面中心力距为：7.331t·m校核水位1082.520水压力=0.5·γ·H 2=7.031t水压力到截面中心力臂为： 1.250m水压力到截面中心力距为：8.789t·m4.1.2应力计算：应力计算参照《土力学》，公式如下：式中：Pmin,Pmax—截面最小、最大压力，Mx —荷载对x—x 轴的力矩，Ix —基础底面积对x—x 轴的惯性矩P=32.3058(正常、设计、校核)A=B×1= 3.000M x= 3.391正常水位7.331设计水位8.789校核水位34.1.1荷载计算(1).永久作用标准值（自重）：永久作用荷载计算分矩形和三角形两部分A 、矩形部分坝顶宽度 3.000m坝顶高程1083.452则截面高17.452m,截面以上矩形面积S 52.356m 2坝体材料容重为γ= 2.300t/m 3所以坝体自重G 1K 为：120.4188t自重到截面中心的力臂L 1为：-5.100m自重到截面中心的力距M 1为：-614.136t·mB 、三角形部分三角形高:12.77截面底宽：13.216则三角形底面宽度=10.216三角形面积S △=65.229坝体材料容重为γ= 2.300t/m 3y I M A P p x x ±=maxmin,所以坝体自重G 2K 为：150.027t自重到截面中心的力臂L 2为：-0.203m自重到截面中心的力距M 2为：-30.405t·m(2).可变作用标准值：正常水位1081.500水压力=0.5·γ·H 2=120.125t水压力到截面中心力臂为： 5.1666667m水压力到截面中心力距为：620.646t·m设计水位1082.300水压力=0.5·γ·H 2=132.845t 水压力到截面中心力臂为：5.433m 水压力到截面中心力距为：721.791t·m校核水位1082.520水压力=0.5·γ·H 2=136.455t水压力到截面中心力臂为： 5.507m水压力到截面中心力距为：751.413t·m4.1.2应力计算：应力计算参照《土力学》，公式如下：式中：Pmin,Pmax—截面最小、最大压力，Mx —荷载对x—x 轴的力矩，Ix —基础底面积对x—x 轴的惯性矩P=120.4188(正常、设计、校核)A=B×1=13.216M x=-23.896正常水位77.250设计水位106.872校核水位3 本工程坝体材料为C10混凝土砌毛石，毛石石料等级为500，查《浆砌石重力坝设计规范》，其允许压力值为，基本组合82.9t/m 2，特殊组合110t/m 2因此，根据上述计算可知，坝体满足最小应力大于0，最大压应力小于坝体允许抗压应力。

坝体强度承载能力极限状态计算及坝体稳定承载能力极限状态计算（一）、基本资料坝顶高程：1107.0 m校核洪水位（P = 0.5 %）上游：1105.67 m下游：1095.18 m 正常蓄水位上游：1105.5 m下游：1094.89 m死水位：1100.0 m混凝土容重：24 KN/m3坝前淤沙高程：1098.3 m泥沙浮容重：5 KN/m3混凝土与基岩间抗剪断参数值：f `= 0.5c `= 0.2 Mpa坝基基岩承载力：［f］= 400 Kpa坝基垫层混凝土：C15坝体混凝土：C1050年一遇最大风速：v 0 = 19.44 m/s多年平均最大风速为：v 0 `= 12.9 m/s吹程D = 1000 m（二）、坝体断面1、非溢流坝段标准剖面(1)荷载作用的标准值计算（以单宽计算）A 、正常蓄水位情况（上游水位1105.5m ，下游水位1094.89m ） ① 竖向力（自重）W 1 = 24×5×17 = 2040 KN W 2 = 24×10.75×8.6 /2 = 1109.4 KNW 3 = 9.81×（1094.5-1090）2×0.8 /2 = 79.46 KN ∑W = 3228.86 KNW 1作用点至O 点的力臂为： (13.6-5) /2 = 4.3 m W 2作用点至O 点的力臂为：m 067.16.83226.13=⨯- W 3作用点至O 点的力臂为：m 6.58.0)10905.1094(3126.13=⨯-⨯-竖向力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OW1 = 2040×4.3 = 8772 KN·mM OW2 = －1109.4×1.067 = －1183.7 KN·mM OW3 = －79.46×5.6 = －445 KN·m∑M OW = 7143.3 KN·m②静水压力（水平力）P1 = γH12 /2 = 9.81×(1105.5－1090)2 /2= －1178.4 KNP2 =γH22 /2 =9.81×(1094.89-1090)2 /2 = 117.3KN∑P = －1061.1 KNP1作用点至O点的力臂为：(1105.5－1090)/3 = 5.167mP2作用点至O点的力臂为：(1094.89－1090)/3 = 1.63m静水压力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OP1 = 1178.4×5.167 = －6089 KN·mM OP2 = 117.3×1.63 = 191.2 KN·m∑M OP = －5897.8 KN·m③扬压力扬压力示意图请见下页附图：H1 = 1105.5－1090 = 15.5 mH2 = 1094.89－1090 = 4.89 m(H1 －H1) = 15.5－4.89 = 10.61 m计算扬压力如下：U1 = 9.81×13.6×4.89 = 652.4 KNU2 = 9.81 ×13.6×10.61 /2 = 707.8 KN∑U = 1360.2 KNU1作用点至O点的力臂为：0 mU2作用点至O点的力臂为：13.6 / 2－13.6 / 3 = 2.267m 竖向力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OU1 = 0 KN·mM OU2 = －707.8×2.267 = －1604.6 KN·m∑M OU = －1604.6 KN·m④浪压力（直墙式）浪压力计算简图如下：由确定坝顶超高计算时已知如下数据：单位：m使波浪破碎的临界水深计算如下：%1%122ln 4h L h L L H m m m cr πππ-+=将数据代入上式中得到： 013.183.02644.783.02644.7ln 4644.7=-+=πππcr H 由判定条件可知，本计算符合⑴H ≥H cr 和H ≥L m /2，单位长度上的浪压力标准值按下式计算：)(41%1Z m W Wkh h L P +=γ 式中：γw ──水的重度 = 9.81 KN/m 3其余计算参数已有计算结果。

作业一重力坝的安全复核某混凝土重力坝为三级建筑物, 坝基设有防渗帷幕及排水设备, 排水孔中线距坝踵7.0m。

挡水坝剖面体形尺寸及设计水位如图，正常蓄水工况，下游无水。

要求: 分别用分项系数极限状态法和单一安全系数法计算分析设计状况（工况）下，挡水重力坝（单宽剖面）的强度和抗滑稳定性：1.列表计算坝体作用荷载，分别考虑和不考虑作用分项系数。

2.用抗剪断公式校核坝基面抗滑稳定安全系数K'是否满足要求。

3.分析坝基面抗滑稳定承载能力极限状态。

4.核算坝趾主应力抗压强度承载能力极限状态。

5. 核算坝踵竖向正应力抗拉正常使用极限状态。

表1计算参数表项目名称参数指标分项系数作用坝体自重砼容重24kN/m3 1.0 静水压力水容重10 kN/m3 1.0 波浪压力吹程3000m，设计风速v=20m/s 1.2 淤沙压力容重 6 kN/m3内摩擦角φn=18° 1.2 渗透压力折减系数α=0.3 1.2性能混凝土抗压强度标准值9.8MPa 1.5 基岩度20MPa 2.0 建基面摩擦系数抗剪f0.7，抗剪断f，0.9 1.3 建基面凝聚力C，0.7 Mpa 3.0结构重要性系数γo 1.0 设计状况系数ψ 1.0结构系数γ d 抗滑稳定极限状态 1.2 抗压强度极限状态 1.8表2计算参考表作用名称计算公式力臂m不计作用分项系数计入作用分项系数竖向力kN水平力kKN基面力矩kN-m竖向力kN水平力kN基面力矩kN-m坝体自重G1 G2 G3静水压力P1 W1 W2淤沙压力Pn Wn浪压力Pl扬压力U1 U2 U3合计。

二、重力坝的应力分析（一）重力坝应力分析的目的和方法应力分析的主要目的是：验算拟定坝体断面是否经济合理；确定坝内材料分区；为某些部位的配筋提供依据。

常用的分析方法有理论计算和模型试验两大类。

中、小型工程，一般采用理论计算方法即可。

理论计算法又包括材料力学法和弹性理论的解析法、有限元法，其中材料力学法是一种简便而较实用的方法。

（二）用材料力学法计算坝体边缘应力材料力学法通常沿坝轴线取单位宽度（1m ）的坝体作为计算对象。

坝体的最大和最小应力一般发生在上、下游坝面，所以，应首先计算坝体边缘应力。

计算简图及荷载、应力的正方向，如图1所示。

图11、水平截面上的边缘正应力yu σ 和yd σ26yu ydWM TTσσ⎧⎫⎪⎪=±⎨⎬⎪⎪⎩⎭∑∑ （6—1）式中W∑——计算截面以上所有垂直分力的代数和（向下为正），kN ；M∑——计算截面以上所有作用力对截面形心的力矩代数和（逆时针方向为正），kN ．m ；T——坝体计算截面沿上下游方向的水平宽度，m ；2、剪应力 u τ和d τ已知u τ 和 d τ以后，可根据边缘微元体的平衡条件解出上、下游边缘剪应力，见图2所示。

由平衡条件0y =∑ 可得：图2()u u y up n τσ=- （6—2） ()d y ddpm τσ=- （6—3）式中 u p 、d p ——计算截面处上、下游坝面的水压力强度（如有泥沙压力和地震水压力时也应计算在内），kPa ；n 、m ——计算截面处上、下游坝面的坡率，tan u n φ= ，tan d m φ=。

3、垂直截面上的边缘正应力 xu σ及xd σ仿照求边缘剪应力的方法，对微分单元体取0x =∑ ，可得：()()2x u u u y up p n k P a σσ=--（6—4） ()()2x d d y ddp pm k P a σσ=+-（6—5）4、边缘主应力 1u σ及1d σ由材料力学可知，主应力作用面上无剪应力，故上、下游坝面即为主应力面之一，另一主应力面与坝面垂直。

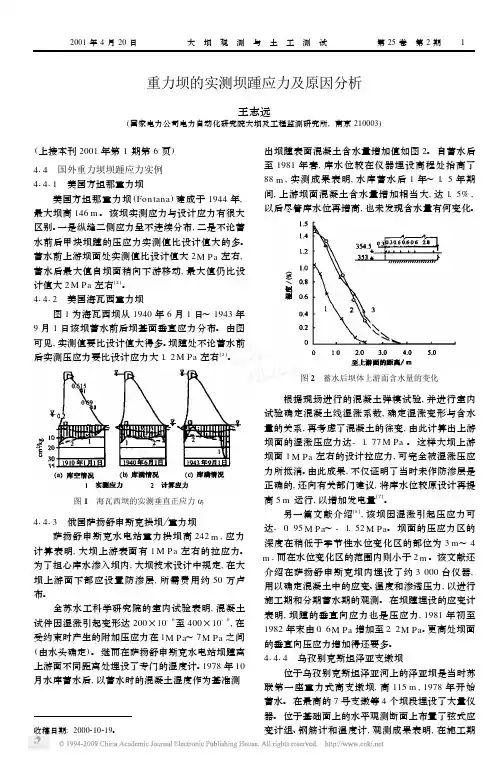
重力坝的实测坝踵应力及原因分析王志远(国家电力公司电力自动化研究院大坝及工程监测研究所,南京210003)收稿日期:2000210219。

(上接本刊2001年第1期第6页)414　国外重力坝坝踵应力实例41411　美国方坦那重力坝美国方坦那重力坝(Fon tana )建成于1944年,最大坝高146m 。

该坝实测应力与设计应力有很大区别。

一是纵缝二侧应力呈不连续分布,二是不论蓄水前后甲块坝踵的压应力实测值比设计值大的多。

蓄水前上游坝面处实测值比设计值大2M Pa 左右,蓄水后最大值自坝面稍向下游移动,最大值仍比设计值大2M Pa 左右[2]。

41412　美国海瓦西重力坝图1为海瓦西坝从1940年6月1日～1943年9月1日该坝蓄水前后坝基面垂直应力分布。

由图可见,实测值要比设计值大得多。

坝踵处不论蓄水前后实测压应力要比设计应力大1.2M Pa 左右[2]。

图1　海瓦西坝的实测垂直正应力Ρy41413　俄国萨扬舒申斯克拱坝 重力坝萨扬舒申斯克水电站重力拱坝高242m ,应力计算表明,大坝上游表面有1M Pa 左右的拉应力。

为了担心库水渗入坝内,大坝技术设计中规定,在大坝上游面下部应设置防渗层,所需费用约50万卢布。

全苏水工科学研究院的室内试验表明,混凝土试件因湿涨引起变形达200×10-6至400×10-6,在受约束时产生的附加压应力在1M Pa ～7M Pa 之间(由水头确定)。

继而在萨扬舒申斯克水电站坝踵离上游面不同距离处埋设了专门的湿度计。

1978年10月水库蓄水后,以蓄水时的混凝土湿度作为基准测出坝踵表面混凝土含水量增加值如图2。

自蓄水后至1981年春,库水位较在仪器埋设高程处抬高了88m ,实测成果表明,水库蓄水后1年～1.5年期间,上游坝面混凝土含水量增加相当大,达1.5%,以后尽管库水位再增高,也未发现含水量有何变化。

图2　蓄水后坝体上游面含水量的变化根据现场进行的混凝土弹模试验,并进行室内试验确定混凝土线湿涨系数,确定湿涨变形与含水量的关系,再考虑了混凝土的徐变,由此计算出上游坝面的湿涨压应力达-1.77M Pa 。

水工建筑物——重力坝习题及答案第二章复习思考题1.结合重力坝的工作条件，分析其优缺点2.重力坝设计必须包括哪些主要内容？3.为什么扬压力对重力坝的应力及稳定均不利？4.画图表示岩基上混凝土实体重力坝设置了封闭的灌浆帷幕、排水孔幕的布置和抽排水设施时的扬压力图形。

5.为什么要进行荷载组合？什么是基本荷载和基本荷载组合，什么是特殊荷载和特殊荷载组合？6.重力坝抗滑稳定计算公式有哪几种？试比较各公式的基本理论、优缺点和适用条件。

7.提高重力坝抗滑稳定性有哪些措施？8.重力坝应力分析的目的是什么？9.重力坝应力分析的材料力学有哪几条基本假定？10.用材料力学法计算重力坝应力，其强度标准是什么？11.重力坝为什么要分缝？需要分哪些缝？12.纵缝有哪几种？各有什么优缺点？13.廊道有哪些作用？如何确定各种用途廊道的形式、尺寸和位置？布置廊道系统的原则是什么？14.坝身排水孔的作用是什么？距上游坝面的距离、孔距如何确定？15.重力坝对地基有哪些要求？为什么有这些要求？这些要求与天然地基的条件之间有哪些矛盾？16.试述重力坝固结灌浆的目的、设计内容、原则和方法。

17.试述重力坝防渗帷幕灌浆的目的、设计内容、原则和方法。

综合测试1.扬压力即为：（A）渗透压力；（B）浮压力；（C）渗透压力和浮压力之和；（D）渗透压力减去浮压力。

2.基本荷载是：（A）出现机会较多的荷载；（B）出现机会较少的荷载；（C）出现机会较多的荷载和出现机会较少的荷载之和；（D）基本荷载和一种或几种特殊荷载。

3.摩擦公式认为：（A）坝体与坝基为胶结状态；（B）坝体与坝基为接触状态；（C）坝体与坝基为连接状态；（D）坝体与坝基为作用状态。

4.材料力学法假定（A）水平截面上的垂直正应力呈曲线分布；（B）水平截面上的垂直正应力呈均匀分布；（C）水平截面上的垂直正应力呈不均匀分布；（D）水平截面上的垂直正应力呈直线分布。

5.应力的控制标准是：（A）上游坝基面垂直正应力（计入扬压力）大于零；（B）上游坝基面垂直正应力（计入扬压力）小于零；（C）上游坝基面垂直正应力（计入扬压力）等于零；（D）上游坝基面垂直正应力（计入扬压力）不为零。

第四节重力坝的应力分析一、应力分析的目的和方法1、目的1°了解坝体内的应力分布情况，检验大坝在施工期和运行期是否满足强度要求；2°为布置坝身材料(如混凝土分区)提供依据；3°为特殊部位的配筋提供依据，如孔口、廊道等部位的配筋；4°为改进结构型式和科学研究提供依据；2、分析方法: 模型试验法和理论计算法①模型试验法光测方法如：偏振光弹性试验, 激光全息试验, 脆性材料电测法②理论计算法1°材料力学法(重力法)这是一种历史悠久、应用最广、最简便的方法。

它不考虑地基变形的影响，假定：σy呈直线分布；σx呈三次抛物线分布；τ呈二次抛物线分布；评价：该法有长期的实践经验，目前我国重力坝设计规范中的强度标准就是以该法为基础的。

2°弹性理论解析法该法的力学模型和数学解法均很严密，但前只有少数边界条件简单的典型结构才有解答。

评价：可用于验证其他方法的精确性，有重要价值。

3°弹性理论差分法该法力学模型严密，在数学解法上采用差分格式，是一种近似的方法。

评价：要求方形网格，对复杂边界适应性差。

4°弹性理论的有限单元法与差分法相反，该法力学模型是近似的，数学解法是精确的，网格可采用三角形单元、四边形单元或两者的组合。

见图2.14评价：可处理复杂的边界条件，随着计算机的发展，单元可划分得很细以模拟各种边界。

目前大型或重要的工程都需用该法计算，以了解坝体各部位的应力状态。

图2.14 重力坝应力分析有限单元法示意图二、材料力学法,见图2.15和图2.161、基本假定①坝体混凝土为均质、连续、各向同性的弹性体②将坝体简化为固结在地基上的变截面悬臂梁；③不考虑地基变形对坝体应力的影响，并认为各坝段独立工作，横缝不传力；④σy呈直线分布；图2.15 坝体应力计算简图图2.16 截面核心计算图2、边缘应力计算①水平截面上的垂直正应力②剪应力③水平正应力④主应力3、内部应力计算图2.17 坝体微元体受力分析①σy的计算, ②τ的计算, ③ σx的计算, ④坝内主应力计算4、考虑扬压力时的计算方法:图2.18 有扬压力的边缘应力计算简图 图2.19 扬压力分布图5、非荷载因素对坝体应力的影响①地基变形对坝体应力的影响,见图2.20图2.20 地基变形示意图 图2.21 坝基对坝体的应力影响②地基不均匀对坝体应力的影响③坝体不同材料对坝体应力的影响④纵缝对坝体应力的影响图2.22纵缝对坝体应力的影响⑤分期施工对坝体应力的影响图2.23分期施工对坝体应力的影响。

水工建筑物课程设计设计题目: 混凝土重力坝的应力分析姓名：学号：年级专业： 2013级水利水电工程指导老师：提交时间： 2016年12月目录一、基本资料 (1)二、确定工程等别和主要建筑物级别 (2)三、非溢流坝剖面尺寸拟定 (3)四、荷载计算及组合 (6)五、抗滑稳定极限状态计算 (7)六、坝址抗压强度极限状态计算 (7)一、基本资料某高山峡谷地区规划的水利枢纽，拟定坝型为混凝土重力坝，其任务以灌溉为主、兼顾供水，水库总库容4亿m3。

1．水电规划成果上游设计洪水位为355.0 m，相应的下游水位为331.0 m；上游校核洪水位356.3 m ，相应的下游水位为332.0 m；正常高水位354.0 m；死水位339.5 m。

2．地质资料：河床高程320.0 m，约有1～2 m覆盖层，基础要求开挖至弱风化层，清基后岩石表面最低高程为318.0m。

岩基为石灰岩，地质构造良好。

坝体和基岩抗剪断摩擦系数f'=0.82，凝聚力c'=0.6MPa。

3．其它有关资料：河流泥沙计算年限采用50年，据此求得坝前淤沙高程330.0 m。

泥沙浮重度为6.5kN/ m3 ，内摩擦角φ=18°。

枢纽所在地区洪水期的多年平均最大风速为15m/s，水库最大风区长度由库区地形图上量得D=0.9km。

坝体混凝土重度γc =24kN/m3，地震设计烈度为4度。

拟采用混凝土强度等级C10，90d龄期，80%保证率，fckd强度标准值为10MPa，坝基岩石允许压应力设计值为4000kPa。

二、确定工程等别和主要建筑物级别（1）水利水电枢纽工程等级划分：根据《水利水电工程等级划分及洪水标准》（SL 252 －2000 ）的规定，水利水电工程根据其工程规模、效益以及在国民经济中的重要性，划分为I、II、III、IV 、V 五等，适用于不同地区、不同条件下建设的防洪、灌溉、发电、供水和治涝等水利水电工程，见表格1：山区、丘陵区水利水电枢纽工程分等指标表格 1工程等别工程规模水库总库容（m）防洪治涝灌溉供水发电保护城镇及工矿企业的重要性保护农田（亩）治涝面积（亩）灌溉面积（亩）供水对象重要性装机容量（）Ⅰ大（1）型10特别重要特别重要Ⅱ大（2）型10 1 重要500100 200150重要120Ⅲ中10.1 中等10030 6050中等30Ⅳ小（1）型0.10.01 一般30 5 155一般5Ⅴ小（2）型0.010.0015对于综合利用的水利水电工程，当按各分项利用项目的分等指标确定的等别不时，其工程等别应按其中的最高等别确定。

碾压混凝土重力坝温度应力分析碾压混凝土重力坝温度应力分析摘要：碾压混凝土重力坝是大型水利工程中常见的一种重要结构形式。

在坝体施工过程中，由于环境条件和材料性能影响，温度变化引起的热应力会对坝体结构产生影响。

本文以某示范性水利工程的碾压混凝土坝为例，通过建立温度场和应力场的数值模型，分析了温度应力对坝体的影响及其变化规律，并提出了相应的控制措施。

1. 引言碾压混凝土重力坝具有结构简单、建造便捷、抗震性能好等优点，在水利工程中得到了广泛应用。

然而，由于环境温度变化等因素的影响，坝体的温度会发生变化，从而产生热应力。

热应力对坝体结构有一定的影响，因此对碾压混凝土重力坝的温度应力进行分析具有重要意义。

2. 碾压混凝土重力坝的温度变化及其影响碾压混凝土重力坝在施工过程中，会受到外界环境温度的影响，从而引起坝体温度的变化。

正常情况下，坝体内部的温度分布会呈现出柱状或螺旋状的分布规律。

温度的变化会引起混凝土的线热应力和面热应力，进而对坝体结构产生影响。

特别是在高温季节，坝体内部的温度急剧升高，热应力会达到较高水平，对坝体的稳定性构成一定的威胁。

3. 温度应力的数值模拟为了分析碾压混凝土重力坝温度应力的变化规律，需要建立相应的数值模型。

首先，通过考虑外界环境温度和材料导热系数等参数，建立坝体温度场的有限元模型。

然后，根据材料力学性质和坝体结构的几何形状，建立应力场的有限元模型。

通过在计算机上进行数值计算，得到了不同温度下的温度场和应力场。

结果显示，在高温季节，坝体内部产生的温度应力较大，对坝体稳定性产生一定的不利影响。

此外，在温度场和应力场的变化过程中，温度应力的分布呈现出非线性变化的趋势。

4. 温度应力的控制措施为了控制温度应力对碾压混凝土重力坝的影响，可以采取以下措施：（1）合理控制混凝土浇筑的温度；（2）采取降温措施，如利用喷淋降温等方法；（3）通过增加混凝土的抗温性能，减小热应力的产生；（4）合理设计坝体结构，降低热应力的传递。

重力坝加高的温度应力问题<关键词：重力坝有限元温控仿真分析1 前言水资源短缺将成为制约我国可持续发展的一个重要因素，随着水资源的不断开发，适合建坝的新坝址越来越少，由于需水量的增长和水库淤积的发展，已建的以供水、灌溉等为目的水库越来越不满足生产与生活用水对水资源的需求，因此己建大坝的加高，将成为未来大坝建设的一个重要任务。

大坝加高在国外已有许多工程先例，如委内瑞拉的古里坝，日本的王泊坝、川上坝、新中野坝，美国的也尔奇坝，印度的科伊纳大坝，瑞士的大狄克桑斯坝等[1] 。

我国大坝加高的实例相对较少，位于大连市郊的英那河大坝加高己于 2001 年开工，南水北调中线方案的龙头工程——丹江口大坝的加高将于近期施工。

重力坝加高会带来三个主要问题，即老坝应力恶化、接合面开裂及新混凝土表面裂缝。

传统上重力坝的加高主要关注老坝体应力恶化的问题，即由于新浇混凝土的温降收缩在老坝体内引起拉应力从而使坝体应力恶化。

解决方法主要从减小新混凝土收缩的影响入手，如在新混凝土内预留竖直宽槽、新老混凝土结合面处设置滑动缝等 [2,3] ，这些方法施工复杂，且只能解决新混凝土沿坝坡方向的收缩带来的不利应力。

加高带来的附加应力分析方法也以简化的算法为主，文献[4] 早在上世纪 60 年代即推导了重力坝加高附加应力的材料力学和弹性力学算法，近期的加高计算开始采用仿真分析的方法，但仍限于平面问题，不能全面地把握加高后的应力问题。

本文通过加高过程的三维仿真分析，研究通过温度控制措施解决加高问题的基本方法。

1 重力坝加高带来的问题1.1 坝踵应力恶化问题新浇混凝土由于水化热的作用温度会升高，后期由于表面散热将会下降到准稳定场。

升温时混凝土龄期短、弹模小而徐变大，且影响仅局限于新浇混凝土附近的局部坝体，不会引起太大的压应力。

但温降时往往坝体已浇筑完成，新混凝土因温降而收缩，从而在老坝体上作用一个向下拉的力，使坝踵产生附加拉应力。

另外，加高时一般不会放空水库，而是保持一定的运行水位，该水位的水压力将全部由老坝承担，新混凝土只分担由加高施工期限制水到最高水位的增量部分，因此加高重力坝的老坝承担更多的水压力而使坝踵应力恶化。

作业一重力坝的稳定应力分析重力坝是一种常见的大坝类型，以其简单、稳定的结构而被广泛应用于工程建设中。

重力坝主要依靠其自身的重量抵抗水压力，保证坝体整体的稳定。

在重力坝的设计和施工过程中，稳定性是一个重要的考虑因素。

稳定性分析可以帮助工程师确定重力坝的最佳尺寸、形状和材料，以确保坝体可以承受水压力和其他外力的作用。

重力坝的稳定性主要包括静力稳定性和动力稳定性两个方面。

静力稳定性分析是指坝体在静止状态下是否能够保持平衡，并通过重力抵抗来抵抗水压力的作用。

动力稳定性分析是指坝体在水流冲击和地震作用下是否能够保持稳定。

在进行重力坝的稳定应力分析时，首先需要确定重力坝的几何形状和材料参数。

重力坝的几何形状包括坝身高度、坝顶宽度、坝底宽度等。

材料参数包括坝体的抗压强度、摩擦角等。

然后，可以使用力学原理和数学方法对坝体进行静力稳定和动力稳定性分析。

静力稳定性分析主要包括重力平衡、摩擦力和附加压力等因素的考虑。

重力平衡要求坝体的重力和水压力之间达到平衡，即满足重力矩平衡和重力力平衡。

摩擦力主要指坝体与地基之间的摩擦力，需要保证摩擦力能够抵抗倾覆力矩的作用。

附加压力是指当坝体的水位发生变化时，由于地下水和孔隙水的作用，会对坝体施加额外的压力，需要考虑这一点来确保稳定。

动力稳定性分析主要包括水流冲击和地震作用的考虑。

在水流冲击分析中，需要考虑水流冲击力对坝体的作用，以及坝体的抗浮力。

地震作用分析中，需要考虑地震对坝体的作用，以及坝体的抗倾覆能力。

除了静力和动力稳定性分析外，还需要考虑其他因素对重力坝的稳定性的影响。

例如，温度变化会导致坝体的膨胀和收缩，可能对坝体结构造成影响，需要考虑温度因素。

此外，地下水位变动、洪水冲刷等等也需要在稳定性分析中进行考虑。

总之，重力坝的稳定力学分析是重力坝设计和施工的重要环节。

通过对重力坝的稳定应力分析，可以确保重力坝能够在不同条件下保持稳定，并能承受各种外力的作用。

这对于保障工程的安全运行和灾害防治具有重要的意义。