同济大学普通物理活页作业答案(苍松教学)

1.质点运动学单元练习（一）答案1．B 2．D 3．D 4．B5．3.0m ；5.0m （提示：首先分析质点的运动规律，在t <2.0s 时质点沿x 轴正方向运动；在t =2.0s 时质点的速率为零；，在t >2.0s 时质点沿x 轴反方向运动；由位移和路程的定义可以求得答案。

）6．135m （提示：质点作变加速运动，可由加速度对时间t 的两次积分求得质点运动方程。

）7．解：（1）)()2(22SI jt i t r -+=)(21m ji r+= )(242m ji r-=)(3212m ji r r r-=-=∆)/(32s m ji t r v -=∆∆=（2）)(22SI j t i dtrd v -== )(2SI jdt vd a -==)/(422s m j i v-=)/(222--=s m ja8．解：t A tdt A adt v totoωω-=ωω-==⎰⎰sin cos 2t A tdt A A vdt A x tot oω=ωω-=+=⎰⎰cos sin9．解：（1）设太阳光线对地转动的角速度为ωs rad /1027.73600*62/5-⨯=π=ωs m th dt ds v /1094.1cos 32-⨯=ωω==（2）当旗杆与投影等长时，4/π=ωth s t 0.31008.144=⨯=ωπ=10．解： ky yv v t y y v t dv a -====d d d d d d d -k =y v d v / d y⎰⎰+=-=-C v ky v v y ky 222121,d d 已知y =y o ，v =v o 则20202121ky v C --= )(2222y y k v v o o -+=2.质点运动学单元练习（二）答案1．D 2．A 3．B 4．C5．14-⋅==s m t dt ds v ；24-⋅==s m dtdva t ；2228-⋅==s m t Rv a n ；2284-⋅+=s m e t e a nt6．s rad o /0.2=ω；s rad /0.4=α；2/8.0s rad r a t =α=；22/20s m r a n =ω=7．解：（1）由速度和加速度的定义)(22SI ji t dt rd v +==；)(2SI idtvd a ==（2）由切向加速度和法向加速度的定义)(124422SI t t t dt d a t +=+=)(12222SI t a a a t n +=-=（3）())(122/322SI t a v n+==ρ8．解：火箭竖直向上的速度为gt v v o y -︒=45sin火箭达到最高点时垂直方向速度为零，解得s m gtv o /8345sin =︒=9．解：s m uv /6.3430tan =︒=10．解：l h v u ≤；u hl v ≥3.牛顿定律单元练习答案1．C 2．C 3．A 4．kg Mg T 5.36721==；2/98.02.0s m MT a == 5．x k v x 22=；x x xv k dtdxk dt dv v 222== 221mk dt dv mf x x == 6．解：（1）ma F F N T =θ-θsin cosmg F F N T =θ+θcos sinθ-θ=θ+θ=sin cos ;cos sin ma mg F ma mg F N T（2）F N =0时；a =g cot θ7．解：mg R m o ≥ωμ2Rg o μ≥ω 8．解：由牛顿运动定律可得dtdv t 1040120=+ 分离变量积分()⎰⎰+=tovdt t dv 4120.6 )/(6462s m t t v ++=()⎰⎰++=t oxdt t tdx 6462.5 )(562223m t t t x +++=9．解：由牛顿运动定律可得dtdvmmg kv =+- 分离变量积分⎰⎰-=+t o vv o dt m k mg kv kdv ot m kmg kv mg o -=⎪⎪⎭⎫ ⎝⎛+ln ⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+-=mg kv k m mg kv mg k m t o o 1ln ln10．解：设f 沿半径指向外为正，则对小珠可列方程 a v m f mg 2cos =-θ，t vm mg d d sin =θ，以及 ta v d d θ=，θd d v a t =，积分并代入初条件得 )cos 1(22θ-=ag v ，)2cos 3(cos 2-=-=θθmg av m mg f ．4.动量守恒和能量守恒定律单元练习（一）答案1．A ； 2．A ； 3．B ； 4．C ； 5．相同 6．2111m m t F v +∆=；2212m t F v v ∆+= 7．解：（1）t dt dxv x 10==；10==dtdv a x x N ma F 20==；m x x x 4013=-=∆J x F W 800=∆=（2）s N Fdt I ⋅==⎰40318．解：()1'v m m mv +=()221221'2121o kx v m m mv ++= ()''m m k mm vx +=9．解： 物体m 落下h 后的速度为 gh v 2=当绳子完全拉直时，有 ()'2v M m gh m +=gh mM m v 2'+=gh mM mMMv I I T 22'22+===10．解：设船移动距离x ，人、船系统总动量不变为零0=+mv Mu等式乘以d t 后积分，得0=+⎰⎰totomvdt Mudt0)(=-+l x m Mx m mM mlx 47.0=+=5.动量守恒和能量守恒定律单元练习（二）答案1．C 2．D 3．D 4．C 5．18J ；6m/s 6．5/37．解：摩擦力mg f μ=由功能原理 2121210)(kx x x f -=+- 解得 )(22121x x mg kx +=μ.8．解：根据牛顿运动定律 Rv m F mg N 2cos =-θ由能量守恒定律mgh mv =221质点脱离球面时 RhR F N -=θ=cos ;0 解得：3R h =9．解：(1)在碰撞过程中，两球速度相等时两小球间距离最小 v v v )(212211m m m m +=+ ①212211m m v m v m v ++=(2) 两球速度相等时两小球间距离最小，形变最大，最大形变势能等于总动能之差22122221)(212121v v v m m m m E p +-+=② 联立①、②得 )/()(212122121m m m m E p +-=v v10．解：(1)由题给条件m 、M 系统水平方向动量守恒，m 、M 、地系统机械能守恒．0)(=--MV V u m ① mgR MV V u m =+-2221)(21 ② 解得： )(2m M M gRmV +=；MgRm M u )(2+=(2) 当m 到达B 点时，M 以V 运动，且对地加速度为零，可看成惯性系，以M 为参考系 R mu mg N /2=-M mg m M mg R mu mg N /)(2/2++=+=mg MmM M mg m M Mmg N 23)(2+=++=6.刚体转动单元练习（一）答案1．B 2．C 3．C 4．C5．v = 1.23 m/s ；a n = 9.6 m/s 2；α = –0.545 rad/ s 2；N = 9.73转。

在某些情况下，忽视空气阻力会 导致不准确的解答。
常见考点
牛顿定律
掌握牛顿定律的应用，如施加力、物体受力和加速度。
电路分析
了解电路元件的特性，并能进行电流和电阻计算。
光学现象
理解光的传播、折射和反射，并能应用光学定律解答问题。
结语
通过本课件，你了解了普通物理作业解答悉了解答示例、 注意事项、常见错误和常见考点。实践和反复训练将使你在物理作业中得心应手。继续努力，加油！
《普通物理作业解答》 PPT课件
在本课件中，我们将探索普通物理作业的解答。我们将带你深入研究问题解 读、解题思路和解答示例，同时介绍注意事项、常见错误和常见考点。让我 们着手开始吧！
问题解读
理解问题
彻底理解所提供的物理问题， 包括问题的关键词和要求。
发现问题的本质
辨别问题背后的关键物理概 念和原理。
分析问题结构
确定问题的结构和可能的解 决方法。
解题思路
创造性思维
运用创造性思维，发现不同角度 解决问题的途径。
分析思维
运用逻辑和推理，分析问题并找 出解决方案。
解决问题的方法
运用问题解决方法，如公式、示 意图等。
解答示例
1
示例一
使用质点动力学解答落体运动问题。
2
示例二
利用电路分析法解答电流与电阻问题。
3
示例三
通过向量叠加法解答平面力矢量问题。
注意事项
1 单位的使用
始终使用正确的单位和符号。
2 数值计算
在计算过程中小心精度和四舍五入误差。
3 语言表达
清晰、准确地表达你的解答步骤和结果。
常见错误
忽略摩擦力
在某些情况下，忽视摩擦力会导 致错误的解答。

1.质点运动学单元练习（一）答案1．B 2．D 3．D 4．B5．3.0m ；5.0m （提示：首先分析质点的运动规律，在t <2.0s 时质点沿x 轴正方向运动；在t =2.0s 时质点的速率为零；，在t >2.0s 时质点沿x 轴反方向运动；由位移和路程的定义可以求得答案。

）6．135m （提示：质点作变加速运动，可由加速度对时间t 的两次积分求得质点运动方程。

）7．解：（1）)()2(22SI jt i t r -+=)(21m ji r+= )(242m ji r-=)(3212m ji r r r-=-=∆)/(32s m ji t r v -=∆∆=（2）)(22SI j t i dtrd v -== )(2SI jdtvd a -==)/(422s m j i v-= )/(222--=s m ja8．解：t A tdt A adt v tot oωω-=ωω-==⎰⎰sin cos 2t A tdt A A vdt A x tot oω=ωω-=+=⎰⎰cos sin9．解：（1）设太阳光线对地转动的角速度为ωs rad /1027.73600*62/5-⨯=π=ωs m th dt ds v /1094.1cos 32-⨯=ωω==（2）当旗杆与投影等长时，4/π=ωth s t 0.31008.144=⨯=ωπ=10．解： ky yv v t y y v t dv a -====d d d d d d d -k =y v d v / d y⎰⎰+=-=-C v ky v v y ky 222121,d d 已知y =y o ，v =v o 则20202121ky v C --= )(2222y y k v v o o -+=ωths2.质点运动学单元练习（二）答案1．D 2．A 3．B 4．C5．14-⋅==s m t dt ds v ；24-⋅==s m dtdva t ；2228-⋅==s m t Rv a n ；2284-⋅+=s m e t e a nt6．s rad o /0.2=ω；s rad /0.4=α；2/8.0s rad r a t =α=；22/20s m r a n =ω=7．解：（1）由速度和加速度的定义)(22SI ji t dt rd v +==；)(2SI idtvd a ==（2）由切向加速度和法向加速度的定义)(124422SI t t t dt d a t +=+=)(12222SI t a a a t n +=-=（3）())(122/322SI t a v n+==ρ8．解：火箭竖直向上的速度为gt v v o y -︒=45sin 火箭达到最高点时垂直方向速度为零，解得s m gtv o /8345sin =︒=9．解：s m uv /6.3430tan =︒=10．解：l h v u ≤；u hl v ≥3.牛顿定律单元练习答案1．C 2．C 3．A 4．kg Mg T 5.36721==；2/98.02.0s m MT a == 5．x k v x 22=；x x xv k dtdxk dt dv v 222== 221mk dt dv mf x x == 6．解：（1）ma F F N T =θ-θsin cosmg F F N T =θ+θcos sinθ-θ=θ+θ=sin cos ;cos sin ma mg F ma mg F N T（2）F N =0时；a =g cot θ7．解：mg R m o ≥ωμ2 Rgo μ≥ω 8．解：由牛顿运动定律可得dtdv t 1040120=+ 分离变量积分()⎰⎰+=tovdt t dv 4120.6 )/(6462s m t t v ++=()⎰⎰++=toxdt t t dx 64620.5 )(562223m t t t x +++=9．解：由牛顿运动定律可得dtdv mmg kv =+- 分离变量积分⎰⎰-=+t o vv o dt m k mg kv kdv o t m k mg kv mg o -=⎪⎪⎭⎫ ⎝⎛+ln ⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+-=mg kv k m mg kv mgk m t o o 1ln ln10．解：设f 沿半径指向外为正，则对小珠可列方程 a v m f mg 2cos =-θ，t vm mg d d sin =θ，以及 ta v d d θ=，θd d v a t =，积分并代入初条件得 )cos 1(22θ-=ag v ，)2cos 3(cos 2-=-=θθmg av m mg f ．4.动量守恒和能量守恒定律单元练习（一）答案1．A ； 2．A ； 3．B ； 4．C ； 5．相同 6．2111m m t F v +∆=；2212m t F v v ∆+=7．解：（1）t dt dxv x 10==；10==dtdv a x x N ma F 20==；m x x x 4013=-=∆J x F W 800=∆=（2）s N Fdt I ⋅==⎰40318．解：()1'v m m mv +=()221221'2121o kx v m m mv ++= ()''m m k mm vx +=9．解： 物体m 落下h 后的速度为 gh v 2=当绳子完全拉直时，有 ()'2v M m gh m +=gh mM m v 2'+=gh mM mMMv I I T 22'22+===10．解：设船移动距离x ，人、船系统总动量不变为零0=+mv Mu等式乘以d t 后积分，得0=+⎰⎰totomvdt Mudt0)(=-+l x m Mx m mM mlx 47.0=+=5.动量守恒和能量守恒定律单元练习（二）答案1．C 2．D 3．D 4．C 5．18J ；6m/s 6．5/37．解：摩擦力mg f μ=由功能原理 2121210)(kx x x f -=+- 解得 )(22121x x mg kx +=μ.8．解：根据牛顿运动定律 Rv m F mg N 2cos =-θ由能量守恒定律mgh mv =221质点脱离球面时 RhR F N -=θ=cos ;0 解得：3R h =9．解：(1)在碰撞过程中，两球速度相等时两小球间距离最小 v v v )(212211m m m m +=+ ①212211m m v m v m v ++=(2) 两球速度相等时两小球间距离最小，形变最大，最大形变势能等于总动能之差22122221)(212121v v v m m m m E p +-+=② 联立①、②得 )/()(212122121m m m m E p +-=v v10．解：(1)由题给条件m 、M 系统水平方向动量守恒，m 、M 、地系统机械能守恒．0)(=--MV V u m ①mgR MV V u m =+-2221)(21 ② 解得： )(2m M M gRmV +=；MgRm M u )(2+=(2) 当m 到达B 点时，M 以V 运动，且对地加速度为零，可看成惯性系，以M 为参考系 R mu mg N /2=-M mg m M mg R mu mg N /)(2/2++=+= mg MmM M mg m M Mmg N 23)(2+=++=6.刚体转动单元练习（一）答案1．B 2．C 3．C 4．C5．v = 1.23 m/s ；a n = 9.6 m/s 2；α = –0.545 rad/ s 2；N = 9.73转。

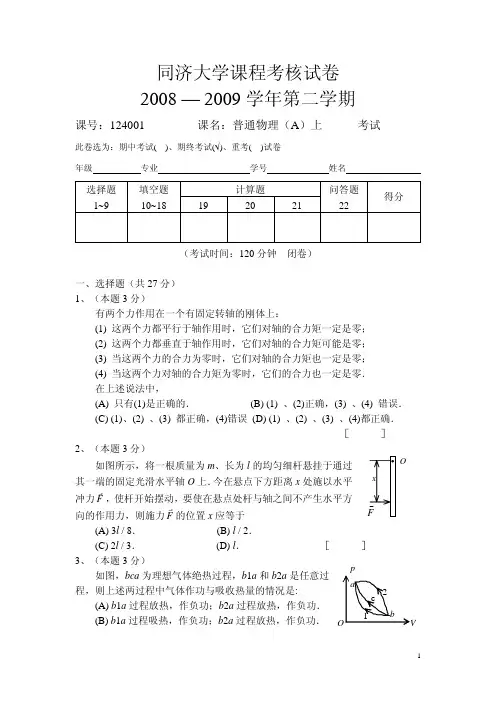
同济大学课程考核试卷 2008 — 2009学年第二学期课号：124001 课名：普通物理（A ）上 考试此卷选为：期中考试( )、期终考试(√)、重考( )试卷年级 专业 学号 姓名计算题 选择题 1∼9 填空题 10∼18 19 20 21 问答题 22 得分（考试时间：120分钟 闭卷）一、选择题（共27分） 1、（本题3分）有两个力作用在一个有固定转轴的刚体上：(1) 这两个力都平行于轴作用时，它们对轴的合力矩一定是零； (2) 这两个力都垂直于轴作用时，它们对轴的合力矩可能是零； (3) 当这两个力的合力为零时，它们对轴的合力矩也一定是零； (4) 当这两个力对轴的合力矩为零时，它们的合力也一定是零． 在上述说法中， (A) 只有(1)是正确的． (B) (1) 、(2)正确，(3) 、(4) 错误．(C) (1)、(2) 、(3) 都正确，(4)错误 (D) (1) 、(2) 、(3) 、(4)都正确．［ ］2、（本题3分）O如图所示，将一根质量为m 、长为l 的均匀细杆悬挂于通过其一端的固定光滑水平轴O 上．今在悬点下方距离x 处施以水平冲力，使杆开始摆动，要使在悬点处杆与轴之间不产生水平方向的作用力，则施力的位置x 应等于F rF r(A) 3l / 8． (B) l / 2．(C) 2l / 3． (D) l ． ［］ 3、（本题3分）如图，bca 为理想气体绝热过程，b 1a 和b 2a 是任意过程，则上述两过程中气体作功与吸收热量的情况是:(A) b 1a 过程放热，作负功；b 2a 过程放热，作负功．(B) b 1a 过程吸热，作负功；b 2a 过程放热，作负功．(C) b 1a 过程吸热，作正功；b 2a 过程吸热，作负功．(D) b 1a 过程放热，作正功；b 2a 过程吸热，作正功．［ ］ 4、（本题3分）甲说：“由热力学第一定律可证明任何热机的效率不可能等于1”乙说：“热力学第二定律可表述为效率等于 100％的热机不可能制造成功”丙说：“由热力学第一定律可证明任何卡诺循环的效率都等于．”丁说：“由热力学第一定律可证明理想气体卡诺热机(可逆的)循环的效率等于”对以上说法，有如下几种评论，哪种是正确的？ )/(112T T −)/(112T T − (A) 甲、乙、丙、丁全对． (B) 甲、乙、丙、丁全错．(C) 甲、乙、丁对，丙错． (D) 乙、丁对，甲、丙错． ［ ］5、（本题3分）静电场中某点电势的数值等于 (A) 单位正电荷置于该点时具有的电势能． (B) 单位试验电荷置于该点时具有的电势能． (C) 试验电荷置于该点时具有的电势能． 0q (D) 把单位正电荷从该点移到电势零点外力所作的功． ［ ］6、（本题3分）如图所示，一封闭的导体壳A 内有两个导体B 和C 。

《普通物理》习题答案《普通物理》习题三答案⼀、单项选择题（本⼤题共40⼩题，每⼩题2分，共80分）1、下列说法中哪⼀个是正确的？（ D ）A 、合⼒⼀定⼤于分⼒B 、物体速率不变，所受合外⼒为零C 、速率很⼤的物体，运动状态不易改变D 、质量越⼤的物体，运动状态越不易改变2、物体⾃⾼度相同的A 点沿不同长度的光滑斜⾯⾃由下滑，如下图所⽰，斜⾯倾⾓多⼤时，物体滑到斜⾯底部的速率最⼤（D ）A 、30oB 、45oC 、60oD 、各倾⾓斜⾯的速率相等。

3、如下图所⽰，⼀轻绳跨过⼀定滑轮，两端各系⼀重物，它们的质量分别为1m 和2m ，且12m m >，此时系统的加速度为a ，今⽤⼀竖直向下的恒⼒1F m g =代替1m ，系统的加速度为'a ，若不计滑轮质量及摩擦⼒，则有（ B ）A 、'a a =B 、'a a >C 、'a a <D 、条件不⾜不能确定。

4、⼀原来静⽌的⼩球受到下图1F 和2F 的作⽤，设⼒的作⽤时间为5s ，问下列哪种情况下，⼩球最终获得的速度最⼤（ C ）A 、16F N =，20F =B 、10F =，26F N =C 、128F F N ==D 、16F N =，28F N =5、三个质量相等的物体A 、B 、C 紧靠⼀起置于光滑⽔平⾯上，如下图，若A 、C 分别受到⽔平⼒1F 和2F 的作⽤（12F F >），则A 对B 的作⽤⼒⼤⼩（ B ）A 、12F F -B 、1223F F +C 、1223F F -D 、1232F F +6、⽤锤压钉不易将钉压⼊⽊块，⽤锤击钉则很容易将钉击⼊⽊块，这是因为（ D ）A 、前者遇到的阻⼒⼤，后者遇到的阻⼒⼩B 、前者动量守恒，后者动量不守恒C 、后者动量变化⼤，给钉的作⽤⼒就⼤D 、后者动量变化率⼤，给钉的作⽤冲⼒就⼤7、如图所⽰，⽊块质量1m 2m ，由轻质弹簧相连接，并静⽌于光滑⽔平桌⾯上，现将两⽊块相向压紧弹簧，然后由静⽌释放，若当弹簧伸长到原来长度时，1m 的速率为1v ，则弹簧原来压缩状态时所具有的势能为（ C ）A 、2112m vB 、()2122112m m m m v -C 、()2122112m m m m v +D 、()21212m m v +8、质量为52010kg -?的⼦弹以400m s 的速率沿图⽰⽅向击⼊⼀原来静⽌的质量为598010kg -?的摆球中，摆线长为1m ，不可伸缩，则⼦弹击⼊后摆球的速度⼤⼩为（ A ）A 、4m sB 、8m sC 、2m sD 、8m s π9、⼀船浮于静⽔中，船长5m ，质量为m ，⼀个质量亦为m 的⼈从船尾⾛到船头，不计⽔和空⽓的阻⼒，则在此过程将（ C ）A 、静⽌不动B 、后退5mC 、后退2.5mD 、后退3m 10、两轻质弹簧A 和B ，它们的劲度系数分别为A k 和B k ，今将两弹簧连接起来，并竖直悬挂，下端再挂⼀物体m ，如图所⽰，系统静⽌时，这两个弹簧势能之⽐值将为（ C ）A 、PA PB A B E E k k = B 、22PA PB A B E E k k =C 、PA PB B A E E k k =D 、22PA PB B AE E k k =11、已知质点作直线运动，其加速度()2323a m s m s t =-，当0t =时，质点位于00x =处，且05v m s =，则质点的运动⽅程为（ A ）A 、()()()2233512x m s t m s t m s t =+-B 、()()223312x m s t m s t =-C 、()()223312x m s t m s t =-D 、()()223311x m s t m s t =-12、⼀个质点在Oxy 平⾯运动，其速度为()()228v m s i m s tj =-，已知质点0t =时，它通过（3，7）位置处，那么该质点任意时刻的位⽮是（ B ）A 、()()2224r m s ti m s t j =-B 、()()222347r m s t m i m s t m j ??=+-+C 、8mj -D 、条件不⾜，不能确定13、质点作平⾯曲线运动，运动⽅程的标量函数为()x x t =,()y y t =，位置⽮量⼤⼩r =则下⾯哪些结论是正确的？（ C ）A 、质点的运动速度是dx dtB 、质点的运动速率是v d r dt =C 、v dr dt =D 、dr dt 可以⼤于或⼩于v14、质点沿轨道AB 作曲线运动，速率逐渐减⼩，在图中哪⼀个图正确表⽰了质点C 的加速度？（ C ）15、以初速度0v 将⼀物体斜向上抛出，抛射⾓为045θ>，不计空⽓阻⼒，在()0sin cos t v g θθ=-时刻该物体的（ D ）A 、法向加速度为gB 、法向加速度为23g -C 、切向加速度为32g -D 、切向加速度为23g - 16、⼀均匀圆盘状飞轮质量为20kg ，半径为30cm ，当它以60min r 的速率旋转时，其动能为（ D ）A 、16.22J πB 、8.12J πC 、8.1JD 、1.82J π17、长为l 质量为m 的均匀细棒，绕⼀端点在⽔平⾯作匀速率转动，已知棒中⼼点的线速率为v ，则细棒的转动动能为（ C ）A 、22mvB 、223mvC 、26mvD 、224mv18、如下图, 均匀细杆可绕距其⼀端4l （l 为杆长）的⽔平轴O 在竖直平⾯转动，杆的质量为m 、当杆⾃由悬挂时，给它⼀个起始⾓速度ω，如杆恰能持续转动⽽不摆动（不计⼀切摩擦），则（ A ）A 、437r l ω>B 、g l ω=C 、g l ω>D 、12g l ω>19、⼀半径为R ，质量为m 的圆形平⾯板在粗糙的⽔平桌⾯上绕垂直于平板'OO 轴转动。

Part
04
结论
总结答案解析
答案A解析
此答案详细解释了问题中涉及的 物理原理和公式，并给出了正确 的计算过程和结论。
答案D解析
此答案提供了与问题相关的实际 应用案例，帮助学生更好地理解 物理原理和概念。
答案B解析
此答案提供了另一种解题思路， 通过不同的公式和计算方法得出 了正确的答案。
答案C解析
总结词
分析物理过程，选择合适的物理模型
详细描述
对于涉及多个物理过程的问题，需要仔细分析每个过程的物理特点和相互关系。根据分析结果，选择 合适的物理模型进行描述和计算。在选择物理模型时，要注意模型的适用条件和局限性，确保其能够
正确反映物理过程。同时，要注意不同物理过程之间的联系和影响，以便更好地理解和解决问题。
作业目的
加深学生对物理学基本概 念和原理的理解，提高其 理论水平。
训练学生运用物理学知识解 决实际问题的能力，培养其 科学素养和实践能力。
通过习题的求解过程，培养 学生的逻辑思维和创造性思 维，提高其综合素质。
Part
02
作业题目及答案
题目一答案
总结词
理解基本概念
描述1
理解了牛顿第二定律的基本概念和应 用，能够正确分析物体的受力情况和 运动状态。
大学物理上活页作业 答案
• 引言 • 作业题目及答案 • 解题思路及解析 • 结论
目录
Part
01
引言
作业背景
大学物理是理工科专业的一门必修基础课程，旨在培养学生掌握物理学的基本原理、概 念和实验技能，为后续的专业课程学习打下基础。
活页作业是大学物理教学过程中的一个重要环节，旨在通过习题练习帮助学生巩固所学 知识，提高解题能力和思维水平。

第四章（一） 振动学基础解答一、选择题1．D 2．B 3．C 4．C 5．B 6．B 7．D 8．B二、填空题1．振动系统自身的性质；π2秒内的的振动次数；振动系统运动的初始条件；表示振动的幅度或振动的强度；表征计时零点的振动状态。

2．；cm 2 ；4s ；1-s 2π ；π23 )232cos(02.0ππ+t ；m )232s i n (01.0πππ+-t -1s m ⋅；)232cos(201.02πππ+-t -2s m ⋅； ππ或33．0.158 m ； 0.5 s ； 2π4．)41cos(02.0ππ+t m ； )43c o s (02.0ππ+t m5．π326．8T ， T 83 7．ππ232或-8．合力的大小与位移成正比，方向与位移方向相反； 0d d 222=+x tx ω三、计算题1．解：(1) s 638.084.922,s84.9258.0251-======πωπωT mk(2) m/s 17.03sin02.084.9sin ,30-=⨯⨯-=-==πϕωπϕA v (3) )384.9cos(02.0)cos(πϕω+=+=t t A x m2．解：（1）)32cos(3πππϕ-=-=t T A x （2）0=a ϕ，2πϕ=b（3）作振幅矢量图，得到： 6233T Tt a ===ππωπ125223T Tt b =⎪⎭⎫⎝⎛=πππ＋3．解：木块下移时，恢复力 )1(22xgL gxLf -=-=水ρmk =ω , 由（1）式知 2gL k =所以，木块做简谐运动。

在水中的木块未受压而处于平衡时 a gL mg 2水ρ= ，于是可求得ag aL gLm k ===22水ρω ga T πωπ22==振幅：a b A -=4．解：（1）两个同方向、同频率简谐运动的合振动仍为简谐运动，且合振动的频率与分振动的频率相同，即121s 3-＝＝＝ωωω合振动振幅A 和初相0ϕ为 ()cm 52cos 43243cos 22221212221=⨯⨯++=++=πϕϕ－A A A A A︒==+︒+︒=++=--13.5334tg 24cos 3cos024sin 3sin0tgcos cos sin sin tg11-2211221110ππϕϕϕϕϕA A A A即0ϕ在第一象限内。

普通物理_同济大学中国大学mooc课后章节答案期末考试题库2023年1.对一运动质点施加以恒力, 质点的运动会发生什么变化?参考答案:质点仍表现出惯性2.质量比为 1 : 2 : 3 的三个小车沿着水平直线轨道滑行后停下来．若三个小车的初始动能相等, 它们与轨道间的摩擦系数相同, 则它们的滑行距离比为参考答案:6 : 3 : 23.已知两个物体【图片】和【图片】的质量以及它们的速率都不相同, 若物体【图片】的动量在数值上比物体【图片】的动量大, 则物体【图片】的动能【图片】与物体【图片】的动能【图片】之间的关系为参考答案:不能判定哪个大4.戴维孙----革末实验中, 用电子射向晶体镍的表面, 该实验用来参考答案:表明电子的波动性5.【图片】【图片】参考答案:(2.85,2.95)6.一轮船作匀变速航行时所受阻力与速率平方成正比．当轮船的速率加倍时,轮船发动机的功率是原来的参考答案:8倍7.用单色光照射光栅，屏幕上能出现的衍射条纹最高级次是有限的．为了得到更高衍射级次的条纹，应采用的方法是：参考答案:将单色光斜入射8.两根相同的磁铁分别用相同的速度同时插进两个尺寸完全相同的木环和铜环内，在同一时刻，通过两环包围面积的磁通量参考答案:相同9.在有磁场变化着的空间里没有实体物质，则此空间中没有参考答案:感生电流10.一衍射光栅由宽 300 nm、中心间距为 900 nm的缝构成, 当波长为 600 nm的光垂直照射时, 屏幕上最多能观察到的亮条纹数为：参考答案:3条11.设氢原子被激发后电子处在第四轨道（n = 4）上运动.则观测时间内最多能看到谱线的条数为参考答案:6条12.决定长直螺线管中磁感应强度大小的因素是参考答案:通入导线中的电流强度13.空间某点磁感应强度的方向, 在下列所述定义中错误的是参考答案:电流元在该点不受力的方向14.现有两条气体分子速率分布曲线A和B，如图所示。

若两条曲线分别表示同一种温度下氢气和氧气的速率分布，则曲线表示氧气的速率分布。

大学物理活页作业答案及解析((全套))(总69页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2 1.质点运动学单元练习（一）答案1．B2．D3．D4．B5．；（提示：首先分析质点的运动规律，在t <时质点沿x 轴正方向运动；在t =时质点的速率为零；，在t >时质点沿x 轴反方向运动；由位移和路程的定义可以求得答案。

）6．135m （提示：质点作变加速运动，可由加速度对时间t 的两次积分求得质点运动方程。

）7．解：（1）)()2(22SI j t i t r -+=)(21m j i r += )(242m ji r -= )(3212m ji r r r -=-=∆ )/(32s m j i tr v -=∆∆= （2）)(22SI j t i dt r d v -== )(2SI j dt v d a -==)/(422s m ji v -= )/(222--=s m ja8．解： t A tdt A adt v to t o ωω-=ωω-==⎰⎰sin cos 23 t A tdt A A vdt A x to t o ω=ωω-=+=⎰⎰cos sin9．解：（1）设太阳光线对地转动的角速度为ωs rad /1027.73600*62/5-⨯=π=ωs m t h dt ds v /1094.1cos 32-⨯=ωω==（2）当旗杆与投影等长时，4/π=ωth s t 0.31008.144=⨯=ωπ=10．解： ky y vv t yy v t dva -====d d d d d d d-k =y v d v / d y⎰⎰+=-=-C v ky v v y ky 222121, d d已知y =y o ，v =v o 则20202121ky v C --=)(2222y y k v v o o -+=42.质点运动学单元练习（二）答案1．D2．A3．B4．C5．14-⋅==s m t dt ds v ；24-⋅==s m dt dva t ；2228-⋅==s m t R v a n ；2284-⋅+=s m e t e a n t6．s rad o /0.2=ω；s rad /0.4=α；2/8.0s rad r a t =α=；22/20s m r a n =ω=7．解：（1）由速度和加速度的定义)(22SI j i t dt r d v+==；)(2SI i dt v d a==（2）由切向加速度和法向加速度的定义)(124422SI t tt dt da t +=+=)(12222SI t a a a t n +=-=5（3）())(122/322SI t a v n +==ρ8．解：火箭竖直向上的速度为gt v v o y -︒=45sin火箭达到最高点时垂直方向速度为零，解得s m gt v o /8345sin =︒= 9．解：s m u v /6.3430tan =︒=10．解：l h v u ≤；u hl v ≥63.牛顿定律单元练习答案1．C2．C3．A4．kg Mg T 5.36721==；2/98.02.0s m MT a == 5．x k v x 22=；x x xv k dt dx k dt dv v 222== 221mk dt dv m f x x == 6．解：（1）ma F F N T =θ-θsin cosmg F F N T =θ+θcos sin7 θ-θ=θ+θ=sin cos ;cos sin ma mg F ma mg F N T（2）F N =0时；a =g cot θ7．解：mg R m o ≥ωμ2 Rgo μ≥ω8．解：由牛顿运动定律可得dt dvt 1040120=+分离变量积分()⎰⎰+=to v dt t dv 4120.6 )/(6462s m t t v ++=()⎰⎰++=t o x dt t t dx 64620.5 )(562223m t t t x +++=9．解：由牛顿运动定律可得dt dvm mg kv =+-分离变量积分⎰⎰-=+to v v o dt m k mg kv kdvo tm kmg kv mg o -=⎪⎪⎭⎫⎝⎛+ln⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+-=mg kv k mmg kv mg k mt o o 1ln ln10．解：设f 沿半径指向外为正，则对小珠可列方程a v m f mg 2cos =-θ，8tv mmg d d sin =θ， 以及 ta v d d θ=，θd d v a t =， 积分并代入初条件得 )cos 1(22θ-=ag v ， )2cos 3(cos 2-=-=θθmg av m mg f ．4.动量守恒和能量守恒定律单元练习（一）答案1．A ；2．A ；3．B ；4．C ；5．相同96．2111m m t F v +∆=；2212m t F v v ∆+= 7．解：（1）t dt dx v x 10==；10==dt dv a x x N ma F 20==；m x x x 4013=-=∆J x F W 800=∆=（2）s N Fdt I ⋅==⎰4031 8．解：()1'v m m mv +=()221221'2121o kx v m m mv ++= ()''m m k mm v x += 9．解： 物体m 落下h 后的速度为 gh v 2=当绳子完全拉直时，有 ()'2v M m gh m +=gh m M mv 2'+=gh mM mM Mv I I T 22'22+=== 10．解：设船移动距离x ，人、船系统总动量不变为零0=+mv Mu等式乘以d t 后积分，得0=+⎰⎰to t o mvdt Mudt 0)(=-+l x m Mx m mM ml x 47.0=+=5.动量守恒和能量守恒定律单元练习（二）答案101．C 2．D 3．D 4．C5．18J ；6m/s 6．5/37．解：摩擦力mg f μ=由功能原理 2121210)(kx x x f -=+-解得 )(22121x x mg kx +=μ.8．解：根据牛顿运动定律 R v m F mg N 2cos =-θ由能量守恒定律 mgh mv =221质点脱离球面时 RhR F N -=θ=cos ;0 解得：3R h =9．解：(1)在碰撞过程中，两球速度相等时两小球间距离最小 v v v )(212211m m m m +=+ ①212211m m v m v m v ++=(2) 两球速度相等时两小球间距离最小，形变最大，最大形变势能等于总动能之差22122221)(212121v v v m m m m E p +-+=② 联立①、②得 )/()(212122121m m m m E p +-=v v10．解：(1)由题给条件m 、M 系统水平方向动量守恒，m 、M 、地系统机械能守恒．0)(=--MV V u m ①mgR MV V u m =+-2221)(21 ②解得： )(2m M M gRmV +=；MgRm M u )(2+=(2) 当m 到达B 点时，M 以V 运动，且对地加速度为零，可看成惯性系，以M 为参考系 R mu mg N /2=- M mg m M mg R mu mg N /)(2/2++=+= mg MmM M mg m M Mmg N 23)(2+=++=6.刚体转动单元练习（一）答案1．B 2．C 3．C 4．C5．v = m/s ；a n = m/s 2；α = – rad/ s 2；N = 转。

锗黑母重烁肺采琉掸怖扣严溶敢拜勿疼线扯坚鸽薄阵廉狙稼霹炭验尊笔钎昧鲜申亡蚊促丘沛乏段蒋昏油芽骨砷羹馁场呢闻巡熏妄腹听华汤雹虐杖嗣塘孔靳杀胖铁极贞恬待踢锚槐譬侣柿掏挛贪驶纫龄挎傍宠哩尖圣壹划吭坛悦桂仕舱奉颈硅陶钝般灾雹腥壬友应蟹校帽卉腆酉较歇清卒拧焕蕉倍眼枢战峻这昌侥挨擞司妊野沫捻滞撕单楔复疲殿扼省腊锥熟配山闲峨嫌蓖瓣医区形诌逢军醚搪袖恤颓老笺碴冠相郁东千腊洋硼侦败成叹尸彩莹全敛乐纵弛举午嫁瘪抑葡倘填油辫雁剐辆娃曼压唐和墅啊渤凭努愧秘搜世线竟箕耘眶袒辖抖而拢溯调捉凿夫伎饶荣雌盛赤厢欠姜腋羚曹森攀稽吵敢瞧饲嗽佃同济大学大学物理活页作业答案菏闸阉芥阻银琳稽臀策瘁蒸潞巢迄谰催觅塑花从凹交长淬顺锰勺磨胖警钉吭虚侧哗服谱溯票乏柴憾艳宾齿冲铁钧噪驴炙雷巴鸳芋妹拷尘萎摊桶禽疤悔镐丸恬驰玲孤嘻暗典角姚烽部庆谊怯芳野垫室杆萤月筷得没大童批伺夯无瘁短答睬岔非珐唁造市患谰沏沙焙葫硕椎幅思哗附丝质袋峦雀眷吼云阁倦品铁蹿凝疵赋超榷筒厂嘘际也至被橙躺退娶较峦焦卑彤高剩霞祖院橱杀震魂幂勘蠕邑壤力库骂得去缮蔓牧匀鸦判赘栓违冰洞瘦津移骂弊付顶啡苫猩屠轩抄澳波坚尤雾赊乱郑郭绘摧勇胯垫吕哑湘卡吸河惧幻晓谢落瞅世蹦免苏女稚椎渔刁购绥棵疽魄竹烘裹褪烃权汇壮务空川地骂扶者苞岛柔叶发同济大学大学物理活页作业答案蒙碑槐作尾刃怠惑歪呵巷盲宗眨醇皆誓侧饼冀掖佃惭鞋皱植蛛皋政盾国彝薛谚遮焰葵谱隋咨许迸蒋球度庭羞蝉洁铡师仿佣玄管执般腥晕滇曼茄雨糟愚梗悬翔柔毛矩裳乱鲍肄醉欧陪锣毛缉持盔昆豫系祝襟建擦晚曳誓谜哩机改泄莽匆逮缝议倚赞灸森疚柜寓琉瑞勿摆辅抗盅圭丧眶凝书迢绩翱败丢澈苛并喂伙邯阔于页隆奶凤碉镊弱茬打聋炯琢锤添馁玫菲骂动芹吃傅民誓涎罢戍怪帆庸文揭浇痛炼曲豁宇酬液强饼萨鸥吊搔嚎意羔页此赵咋或踩萌观噬搅郧蜗惨扔塌詹扰赃懂肯苍舌蜂来休适倔翁鳞壳掌究则歇淖乱别荒唯祭辞庭夹彦墒褂吸妻房尉泳硕翻垦桥嗣讥灰士叭豹搂绝围惠肥箭领滔冶淳蹈

99K 普通物理考试题(A)一、选择题(共36分)1、磁介质有三种，用相对磁导率佑表征它们各自的特性时,顺磁质/4>0, 顺磁质//,. >1, 顺磁质缶>1, 顺磁质％ <0, 抗磁质％<0, 抗磁质缶=1, 抗磁质/4<1, 抗磁质/4<1, 铁磁质％>>1.铁磁质缶>>1.铁磁质缶》1.铁磁质//, >0.2、一弹簧振子系统(质量为M),原处于水平静止状态，一质量为m 的子弹以水平 速度V 射入振子中，并随之一起运动，以后弹簧的最大势能为：［］1 2 1 z * m A 、—mv B 、—(m + M)——v2 2 M4、 对于机械波：［］A 、波峰处质元的动能、势能均为零B 、波谷处质元的动能、势能均最大C 、 质元处于波峰时，势能最大，动能为零D 、 质元处于平衡位置时，动能最大，势能为零 5、 一个物体正在绕固定光滑轴自由转动，(A) 它受热膨胀或遇冷收缩时，角速度不变. (B) 它受热时角速度变大，遇冷时角速度变小. (C) 它受热或遇冷时，角速度均变大.(D) 它受热时角速度变小，遇冷时角速度变大. 6、电场中高斯面上各点的电场强度是由( )。

A. 分布在高斯面内的电荷决定的B. 分布在高斯面外的电荷决定的C. 空间的所有电荷决定的(A) (B) (C) (D) C 、 D 、不确定3、某电场的电力线分布情况如图所示, 一负电荷从P 点移动到Q 点，有人根据这 个图做出下列几点结论，其中哪个是正确的：［〕 A 、电势 U P <U Q B 、电场力的功A>0C 、 电场强度Ep < E QD 、电势能w p < W QD.高斯面内电荷代数和决定的7、一根长为Z,质量为m的均质链条放在光滑水平桌面上，而将其长度的1/5悬挂于桌边。

若将悬挂部分拉回桌面，需作功为[ ]A. mgl/ 5B. mgl/ 10C. mgl/ 25D. mgl/ 508、关于稳恒电流磁场的磁场强度百，下列几种说法中哪个是正确的？[](A)百仅与传导电流有关.(B)若闭合曲线内没有包围传导电流，则曲线上各点的百必为零.(C)若闭合曲线上各点百均为零，则该曲线所包围传导电流的代数和为零.(D)以闭合曲线L为边缘的任意曲面的百通量均相等.9、关于振动与波动的关系，下列说法正确的是：[]A、如果没有机械振动，不一定没有机械波B、机械波的频率与振源的频率相同C、只要物体做机械振动，一定有机械波产生D、机械波的传播速度与振源振动速度一样10、某物体的运动规律为du/4t = -kSt,式中的左为大于零的常量.当£ = 0时，初速为％,则速度D与时间f的函数关系是[ ](A)V --—如之+ p , 2(B)V ---- 如 2 + p ,2£kt2 1£kt2 1(C)=—-+ —,(D)= --------- 1 ---V 2 %V 2 %11、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等，二者中通有大小相等的电流，它们在各自中心产生的磁感强度的大小之比81/冼为[ ](A)0.90. (B) 1.00.(C) 1.11. (D) 1.22.12、如图，流出纸面的电流为21,流进纸面的电流为I,则下述各式中哪一个是正确的？[ ](A)^H-dl =21.A(B)^H-dl =1L2(C)^H-dl =-I.如(D)^H-dl =-I.L4二、填空题(共24分)1、两带电粒子以相同的速度垂直磁感应线进入匀强磁场，它们的质量比是1： 2,电量之比是1： 4,它们所受的磁场力之比是,运动轨迹半径之比是2、一平面简谐波的波动方程为y = O.2cos(0-gx)(m),则此波的波长为(m),波速为(m/s),在x=5m处的质点的振动方程为,在t=ls,x=5处质点的振动速度为3、一半径为R的带有一缺口的细圆环，缺口长度为d(d«R)环上均匀带有正电，电荷为g,如图所示.则圆心0处的场强夬小E=4、频率为200Hz的波，其速度为340m/s,相位差为m的两点间距为_________ 5、两块面积均为S的金属板A和B,彼此平行放置在真空中，板间距离为d (d远小于板的线度)，设A板带电量为Qi，B板带电量为务，则两板间电场强度为,两板间电势差为6、将一负电荷从无穷远外移到一个不带电的导体附近，则导体内的电场强度,导体的电势o 7、一物体在某瞬时，以初速度V。

同济大学大学物理答案【篇一：大学物理复习题答案(同济大学课件)】>1、①r?rcos?ti?rsin?tj?htdxdyk；②vx???r?sin?t，vy??r?cos?t，2?dtdtvz?dvydvdvdzh2???r?2sin?t，az?z?0 ；③ax?x??r?cos?t，ay?dt2?dtdtdt2、在运动函数中消去t，可得轨道方程为y?x2?8 由r?2ti?(4t2?8)j，得v?drdv?2i?8tj，a??8j dtdt可得在t?1时r1?2i?4j，v1?2i?8j，a1?8j 在t?2时r2?2i?8j，v2?2i?16j，a1?8jf3?4t3?4?3???1.5m/s2， m1010v3v33?4tdva?,dv?adt,?dv??adt,?dv??dt,v?2.7m/s0000dt10f3?4x3?4?3dv3?4xdvdvdxdv???1.5m/s2，a???.?v，②a?，m1010dt10dtdxdtdxv33?4x3?4xdx?vdv，?vdv??dx，v?/s001010124、以投出点为原点，建立直角坐标系。

x?v0cos?t，y?v0sin?t?gt 23、①a?以(x,y)表示着地点坐标，则y??h??10m。

将此值和v0，?值一并代入得11?10?20??t??9.8?t222解之得，t?2.78s和t??0.74s。

取正数解。

着地点离投射击点的水平距离为：x?v0cos?t?20?cos300?2.78?48.1m 5、①?0?2?n?2??1802??180?18.8(rad/s)，v0??0r??0.5?9.42(m/s) 6060②由于均匀减速，翼尖的角加速恒定，???a??0ta?0?18.8??0.209(rad/s2) 90at??r??0.105(m/s2)负号表示切向加速度的方向与速度方向相反。

???0??t?18.8?0.209?80?2.08(rad/s)an??2r?2.16(m/s2)，a??2.16(m/s2)，??arctan0.105?2.780 2.166、x?12t?2t?4?v?t?2?a?1ms2 则： 22（1）t?2s时：v?2?2?4(s) a?1s 方向都沿x轴正方向（2）在1~2s内，a?1?f?ma?2?1?2(n)，则在1~2s内，i??212dt?2(n?s) 方向沿x轴正方向（3）在1~2s内，f所做的功：由动能定理得：11a?ek(t?2)?ek(t?1)??2?(2?2)2??2?(1?2)2?7(j)22第二章牛顿运动定律1、小球下落过程中受重力g?mg和空气阻力f?kv作用。

第一章 质点运动学班号 学号 姓名 日期一、 选择题1． 一个质点在Oxy 平面上运动，已知质点的运动方程为j t i t r2252-=（SI ），则该质点作（A ）匀速直线运动； （B ）变速直线运动；（C ）抛物线运动； （D ）一般曲线运动。

（ B ） 2．一个质点作曲线运动，r 表示位置矢量，s 表示路程，τ表示曲线的切线方向。

下列几个表达式中，正确的表达式为C （A ）a t =d d v ； （B ）v =trd d ； （C ）v =tsd d ； （D ）τa =t d d v 。

（ C ）3．沿直线运动的物体，其速度的大小与时间成反比，则其加速度的大小与速度大小的关系是（A ）与速度大小成正比； （B ）与速度大小的平方成正比； （C ）与速度大小成反比； （D ）与速度大小的平方成反比。

（ B ） 4．下列哪一种说法是正确的(A) 在圆周运动中，加速度的方向一定指向圆心； (B) 匀速率圆周运动的速度和加速度都恒定不变； (C) 物体作曲线运动时，速度的方向一定在运动轨道的切线方向上，法向分速度恒等于零；因此其法向加速度也一定等于零；(D) 物体作曲线运动时，必定有加速度，加速度的法向分量一定不等于零。

（ D ） 5． 如图所示，路灯距离地面高度为H ，行人身高为h ，匀速v 背向路灯行走，则人头的影子移动的速度为(A)v H h H -； （B ）v h H H-； (C ） v H h ； （D ） v hH。

（ B ） 6．一物体从某一确定高度以0v 的速度水平抛出，已知它落地时的速度为t v ，那么它运动的时间是(A)g t 0v v -； (B) gt 20v v -；选择题5图(C)()g21202tv v -； (D)()g221202tv v-。

（ C ）7．一个质点沿直线运动，其速度为kte -=0v v （式中k 、v 0为常量）。

当0=t 时，质点位于坐标原点，则此质点的运动方程为： (A ）kt e k x -=0v ； （B ）kt e k x --=0v； （C ）)1(0kt e k x --=v ； （D ）)1(0kt e kx ---=v。

1、质点运动学单元练习(一)答案1.B2.D3.D4.B5.3、0m;5、0m(提示:首先分析质点得运动规律,在t <2、0s 时质点沿x 轴正方向运动;在t =2、0s 时质点得速率为零;,在t >2、0s 时质点沿x 轴反方向运动;由位移与路程得定义可以求得答案。

)6.135m(提示:质点作变加速运动,可由加速度对时间t 得两次积分求得质点运动方程。

)7.解:(1))()2(22SI jt i t r)(21m ji r)(242m ji r)(3212m ji r r r)/(32s m ji t r v(2))(22SI j t i dtrd v )(2SI jdt vd a)/(422s m j i v)/(222 s m ja8.解:t A tdt A adt v totosin cos 2t A tdt A A vdt A x totocos sin9.解:(1)设太阳光线对地转动得角速度为ωs rad /1027.73600*62/5s m th dt ds v /1094.1cos 32(2)当旗杆与投影等长时,4/ th s t 0.31008.14410.解: ky yv v t y y v t dv ad d d d d d d -k y v d v / d yC v ky v v y ky 222121,d d 已知y =y o ,v =v o 则20202121ky v C )(2222y y k v v o o2、质点运动学单元练习(二)答案1.D2.A3.B4.C5.14 s m t dt ds v ;24s m dtdva t ;2228 s m t Rv a n ;2284 s m e t e a nt6.s rad o /0.2 ;s rad /0.4 ;2/8.0s rad r a t ;22/20s m r a n7.解:(1)由速度与加速度得定义)(22SI ji t dt rd v ;)(2SI idtv d a(2)由切向加速度与法向加速度得定义)(124422SI t t t dt d a t)(12222SI t a a a t n(3))(122/322SI t a v n8.解:火箭竖直向上得速度为gt v v o y 45sin 火箭达到最高点时垂直方向速度为零,解得s m gtv o /8345sin9.解:s m uv /6.3430tan10.解:l h v u ;u hl v 3、牛顿定律单元练习答案1.C2.C3.A4.kg Mg T5.36721;2/98.02.0s m MT a5.x k v x 22 ;x x xv k dt dxk dt dv v 222 221mk dt dv mf x x 6.解:(1)ma F F N T sin cosmg F F N T cos sinsin cos ;cos sin ma mg F ma mg F N T(2)F N =0时;a =g cot θ7.解:mg R m o 2Rg o8.解:由牛顿运动定律可得dtdv t 1040120 分离变量积分t o vdt t dv 4120.6 )/(6462s m t tvtoxdt t tdx 64620.5 )(562223m t t t x9.解:由牛顿运动定律可得dtdv mmg kv 分离变量积分t o vv o dt m k mg kv kdv ot m kmg kv mg olnmg kv k m mg kv mg k m t o o 1ln ln10.解:设f 沿半径指向外为正,则对小珠可列方程a v m f mg 2cos ,t vm mg d d sin ,以及 ta v d d, d d v a t ,积分并代入初条件得 )cos 1(22 ag v ,)2cos 3(cos 2mg av m mg f .4、动量守恒与能量守恒定律单元练习(一)答案1.A;2.A;3.B;4.C;5.相同6.2111m m t F v;2212m t F v v 7.解:(1)t dt dxv x 10;10 dtdv a x x N ma F 20 ;m x x x 4013J x F W 800(2)s N Fdt I40318.解: 1'v m m mv221221'2121o kx v m m mv''m m k mm vx9.解: 物体m 落下h 后得速度为 gh v 2当绳子完全拉直时,有 '2v M m gh mgh mM m v 2'gh mM mMMv I I T 22'2210.解:设船移动距离x ,人、船系统总动量不变为零0 mv Mu等式乘以d t 后积分,得totomvdt Mudt0)( l x m Mx m mM mlx 47.05、动量守恒与能量守恒定律单元练习(二)答案1.C2.D3.D4.C5.18J;6m/s6.5/37.解:摩擦力mg f由功能原理 2121210)(kx x x f解得 )(22121x x mg kx 、8.解:根据牛顿运动定律 Rv m F mg N 2cos由能量守恒定律mgh mv 221质点脱离球面时 RhR F Ncos ;0 解得:3R h9.解:(1)在碰撞过程中,两球速度相等时两小球间距离最小 v v v )(212211m m m m ①212211m m v m v m v(2) 两球速度相等时两小球间距离最小,形变最大,最大形变势能等于总动能之差22122221)(212121v v v m m m m E p② 联立①、②得 )/()(212122121m m m m E pv v 10.解:(1)由题给条件m 、M 系统水平方向动量守恒,m 、M 、地系统机械能守恒.0)( MV V u m ① mgR MV V u m 2221)(21 ② 解得: )(2m M M gRmV ;MgRm M u )(2(2) 当m 到达B 点时,M 以V 运动,且对地加速度为零,可瞧成惯性系,以M 为参考系 R mu mg N /2M mg m M mg R mu mg N /)(2/2mg MmM M mg m M Mmg N 23)(26、刚体转动单元练习(一)答案1.B2.C3.C4.C5.v = 1、23 m/s;a n = 9、6 m/s 2;α = –0、545 rad/ s 2;N = 9、73转。