下载文档原格式
时钟问题是研究钟面上时针和分针关系的问题。
钟面的一周分为60格。
当分针走60格时，时针正好走5格，所以时针的速度是分针的5÷60=1/12，分针每走60÷（1－5/60）=65+5/11（分），与时针重合一次，时钟问题变化多端，也存在着不少学问。
这里列出一个基本的公式：在初始时刻需追赶的格数÷（1－1/12）=追及时间（分钟），其中，1－1/12为每分钟分针比时针多走的格数。
一分钟分针可以走6度，时针可以走0.5度。
常见的时钟问题：求某一时刻时针与分针的夹角，两针重合，两针垂直，两针成直线等类型，此外还有快慢钟问题。
【例1】★有一座时钟现在显示10时整．那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合?【解析】在lO 点时，时针所在位置为刻度10，分针所在位置为刻度12；当两针重合时，分针必须追上50个小刻度，设分针速度为“l ”，有时针速度为“112”，于是需要时间：1650(1)541211÷-=．所以，再过65411分钟，时针与分针将第一次重合．第二次重合时显典型例题知识梳理然为12点整，所以再经过65(1210)6054651111-⨯-=分钟，时针与分针第二次重合．标准的时钟，每隔56511分钟，时针与分针重合一次．我们来熟悉一下常见钟表(机械)的构成：一般时钟的表盘大刻度有12个，即为小时数；小刻度有60个，即为分钟数．所以时针一圈需要12小时，分针一圈需要60分钟(1小时)，时针的速度为分针速度的112．如果设分针的速度为单位“l”，那么时针的速度为“112”．【小试牛刀】钟表的时针与分针在4点多少分第一次重合？【解析】此题属于追及问题，追及路程是20格，速度差是11111212-=，所以追及时间是：11920211211÷=（分）。
【例2】★钟表的时针与分针在8点多少分第一次垂直？【解析】32711，此题属于追及问题，但是追及路程是4401525-=格（由原来的40格变为15格），速度差是11111212-=，所以追及时间是：11325271211÷=（分）。
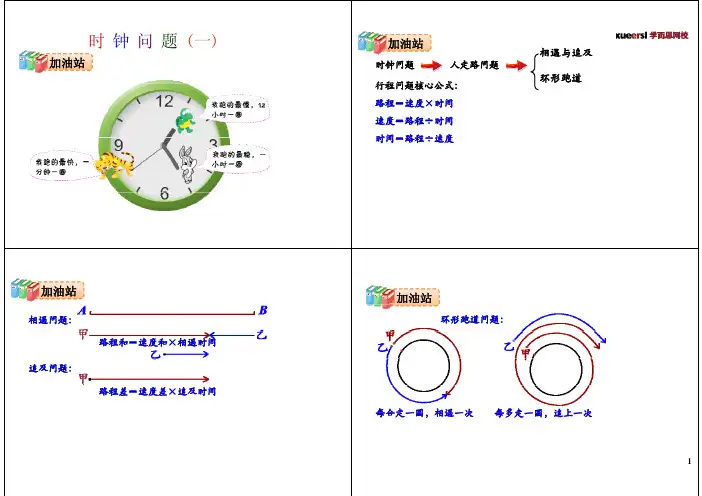
加油站
加油站
行程问题核心公式时钟问题
行程问题核心公式：路程＝速度×时间速度＝路程÷时间时间＝路程÷速度
加油站
相遇问题：
路程和＝速度和×相遇时间
追及问题：
路程差＝速度差×追及时间
加油站
环形跑道问题：
每合走一圈相遇一次每多走一圈追上一次每合走一圈，相遇一次每多走一圈，追上一次
现在是2点，从现在开始，分针与时针在什么时刻第一次重合在一起？
现在是7点40分，从现在开始过多长时间时针与分针第一次重合？
一个时钟现在显示的时间是3点整，请问：再经过多少分钟后，时针与2点钟以后，什么时刻分针与时针第一次成直角？什么时刻第二次成直
不到一个小时后回海海中午去吃饭，出门时看了一下表，是11点多钟。
不到一个小时后回来，发现这时时针与分针恰好交换了位置。
问海海出门多长时间？
在3点到4点之间有一时刻，时针与分针关于“6”对称。
请问：这一时
本讲总结
时钟问题→环形跑道上的相遇追及
追及→重合；成角度。
五年级数学时钟相遇与追及问题(含答案)时钟问题是关于时针和分针的追及或相遇问题，可以看作是一个特殊的圆形轨道问题。
时钟问题包括时钟的快慢、周期和时针与分针所成的角度等。
不同于其他行程问题，时钟问题的速度和总路程的度量方式是指针“每分钟走多少角度”或“每分钟走多少小格”，其中分针速度为每分钟走1小格或6度，时针速度为每分钟走1/12小格或0.5度。
但是对于一些“怪钟”或“坏了的钟”，它们的速度可能与常规时钟不同，需要进行独立分析。
时钟问题可以视为行程问题，其中分针快，时针慢，因此分针与时针的问题就是追及问题。
解决时钟的快慢问题时，可以使用十字交叉法。
例如，在标准时钟中，时针与分针从一次重合到下一次重合所需时间为65.5分。
例1中，当时钟表示1点45分时，时针和分针所成的钝角为142.5度。
例2中，时针、分钟和秒针转动的圈数之和为1466圈，求这段时间有多少秒。
解答中，它们的速度比为1:12:720，因此秒针转了1440圈，即秒。
在一段时间里，时针、分钟、秒针正好走了3665小格，那么这段时间有多少秒？解析：它们的速度比为1:12:720，所以秒针转了3665÷（720+12+1）×720=3600小格，即3600秒。
答案：3600秒。
有一座时钟现在显示10时整。
那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合？解析：在10点时，时针所在位置为刻度10，分针所在位置为刻度12；当两针重合时，分针必须追上50个小刻度，设分针速度为“l”，有时针速度为“l/12”，再过54/11分钟，时针与分针将第一次重合。
第二次重合时显然为12点整，所以再经过65分钟，时针与分针第二次重合。
标准的时钟，每隔65分钟，时针与分针重合一次。
答案：54分钟。
钟表的时针与分针在4点多少分第一次重合？解析：此题属于追及问题，追及路程是20格，速度差是1/11.如果设分针的速度为单位“l”，那么时针的速度为“l/12”。
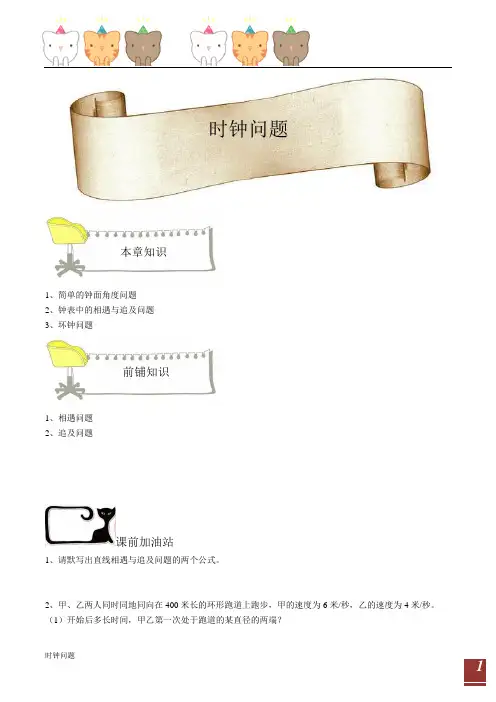
时钟问题本章知识1、简单的钟面角度问题2、钟表中的相遇与追及问题3、坏钟问题前铺知识1、相遇问题2、追及问题课前加油站1、请默写出直线相遇与追及问题的两个公式。
2、甲、乙两人同时同地同向在400米长的环形跑道上跑步，甲的速度为6米/秒，乙的速度为4米/秒。
（1）开始后多长时间，甲乙第一次处于跑道的某直径的两端？（2）开始后多长时间，甲第一次超过乙？（3）开始后多长时间，甲乙第一次处于起点所在的直径对称的位置？要研究时钟某个时刻时针与分针成什么角度，我们首先要知道时针与分针行走的速度。
它们的速度有两种表达形式：以小格/分钟为单位或以角度/分钟为单位。
格 度 时钟一圈60格 360度 时针速度121格/分钟 21度/分钟 分针速度1格/分钟 6度/分钟时针速度：分针速度=1:12。
牢记它有助于我们记忆时针和分针的速度。
1、已知：钟表上60小格，一圈是360度，则分针1小时转多少度？时针1小时转多少度？分针速度是时针速度的多少倍？【演练】分针1分转多少度？时针1分转多少度？时针速度是分针速度的几分之几？2、3:00时，分针落后时针 度，15分钟内，分针走 度，时针走 度，因此3:15时，时针与分针的夹角是 度。
模块1简单的钟面角度问题【演练】在下表中仿照第二行的例子填入适当的算式。
X ：Y （X 点Y 分） X 点时两针的角度 Y 分时时针走的度数 Y 分时分针走的度数 X 点Y 分时两针的度数4:16 4×30=120 16×6=96 16×0.5=8 120-96+8=328:123:409:10【演练】当时钟表示1点45分时，时针和分针所成的钝角是多少度？【演练】在16点16分这个时刻，钟表盘面上时针和分针的夹角是多少度？3、小明家的时钟正对着衣柜上的镜子，某天早上起床时，小明看到镜子中的时钟两针指向5点20分的位置，那么现在真正的时钟显示的时间是？题型一 重合问题公式：分针到时针相差的格数÷（1-121）=重合分钟数分针到时针相差的度数÷（6-0.5）=重合分钟数1、现在是2点，从现在开始，分针与时针什么时刻第一次重合在一起？第二次呢？模块2 钟表中的相遇与追及问题【演练】现在是7点40分，从现在开始过多长时间时针与分针第一次重合？【演练】有一座时钟现在显示10时整。
第十一讲时钟问题内容提要【基本概念】基本思路：封闭曲线上的追及或者相遇问题关键问题：①确定分针与时针的路程差②确定分针与时针的初始位置【基本知识点】具体为：整个钟面为360度，上面有12个大格，每个大格为30度；60个小格，每个小格为6度。
分针速度：每分钟走1小格，每分钟走6度小格，每分钟走0.5度时针速度：每分钟走112【例1】王叔叔有一只手表，他发现手表比家里的闹钟每小时快30 秒.而闹钟却比标准时间每小时慢30 秒，那么王叔叔的手表一昼夜比标准时间差多少秒？【巩固1】小强家有一个闹钟，每时比标准时间快3分。
有一天晚上10点整，小强对准了闹钟，他想第二天早晨6∶00起床，他应该将闹钟的铃定在几点几分？【巩固2】小翔家有一个闹钟，每时比标准时间慢3分。
有一天晚上9点整，小翔对准了闹钟，他想第二天早晨6∶30起床，于是他就将闹钟的铃定在了6∶30。
这个闹钟响铃的时间是标准时间的几点几分？【巩固3】当时钟表示1点45分时，时针和分针所成的钝角是多少度？【例2】现在是3点，什么时候时针与分针第一次重合？【巩固1】钟表的时针与分针在4点多少分第一次重合？【巩固2】有一座时钟现在显示10时整．那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合?【例3】在10点与11点之间，钟面上时针和分针在什么时刻垂直？【巩固1】钟表的时针与分针在8点多少分第一次垂直？【巩固2】2点钟以后，什么时刻分针与时针第一次成直角？【例4】在9点与10点之间的什么时刻，分针与时针在一条直线上？【巩固1】现在是10点，再过多长时间，时针与分针将第一次在一条直线上？【例4 】小明在7点与8点之间解了一道题，开始时分针与时针正好成一条直线，解完题时两针正好重合，小明解题的起始时间？小明解题共用了多少时间？【巩固1】晚上8点刚过，不一会小华开始做作业，一看钟，时针与分针正好成一条直线。
做完作业再看钟，还不到9点，而且分针与时针恰好重合。
第讲时钟问题9 •内容提要【基本概念】基本思路：封闭曲线上的追及或者相遇问题关键问题：①确定分针与时针的路程差②确定分针与时针的初始位置【基本知识点】具体为：整个钟面为360度，上面有12个大格，每个大格为30度；60个小格，每个小格为6度。
分针速度：每分钟走1小格，每分钟走6度、1 、时针速度：每分钟走一小格，每分钟走0.5度【例1】王叔叔有一只手表，他发现手表比家里的闹钟每小时快30秒•而闹钟却比标准时间每小时慢30秒，那么王叔叔的手表一昼夜比标准时间差多少秒？【巩固1】小强家有一个闹钟，每时比标准时间快3分。
有一天晚上10点整，小强对准了闹钟，他想第二天早晨6 : 00起床，他应该将闹钟的铃定在几点几分？【巩固2】小翔家有一个闹钟，每时比标准时间慢3分。
有一天晚上9点整，小翔对准了闹钟，他想第天早晨6 : 30起床，于是他就将闹钟的铃定在了 6 : 30。
这个闹钟响铃的时间是标准时间的几点几分？【巩固3】当时钟表示1点45分时，时针和分针所成的钝角是多少度？【例2】现在是3点，什么时候时针与分针第一次重合？【巩固1】钟表的时针与分针在4点多少分第一次重合？【巩固2】有一座时钟现在显示10时整•那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合？【例3】在10点与11点之间，钟面上时针和分针在什么时刻垂直？【巩固1】钟表的时针与分针在8点多少分第一次垂直？【巩固2】2点钟以后，什么时刻分针与时针第一次成直角？【例4】在9点与10点之间的什么时刻，分针与时针在一条直线上？【巩固1】现在是10点，再过多长时间，时针与分针将第一次在一条直线上？【例4】小明在7点与8点之间解了一道题，开始时分针与时针正好成一条直线，解完题时两针正好重合，小明解题的起始时间？小明解题共用了多少时间？【巩固1】晚上8点刚过，不一会小华开始做作业，一看钟，时针与分针正好成一条直线。
做完作业再看钟，还不到9点，而且分针与时针恰好重合。
- 1 - 精品资料之奥数培优讲义适用：华杯、希望、年级：五年级科目：小学奥数内容：奥数培优教程（资料来源于学校内部，供各位老师学习交流使用，欢迎大家下载参考）时钟问题是研究钟面上时针和分针关系的问题。
钟面的一周分为60格。
当分针走60格时，时针正好走5格，所以时针的速度是分针的5÷60=1/12，分针每走60÷（1－5/60）=65+5/11（分），与时针重合一次，时钟问题变化多端，也存在着不少学问。
这里列出一个基本的公式：在初始时刻需追赶的格数÷（1－1/12）=追及时间（分钟），其中，1－1/12为每分钟分针比时针多走的格数。
一分钟分针可以走6度，时针可以走0.5度。
常见的时钟问题：求某一时刻时针与分针的夹角，两针重合，两针垂直，两针成直线等类型，此外还有快慢钟问题。
【例1】★有一座时钟现在显示10时整．那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合?【解析】在lO点时，时针所在位置为刻度10，分针所在位置为刻度12；当两针重合时，分针必须追上50个小刻度，设分针速度为“l”，有时针速度为“112”，于是需要时间：1650(1)541211÷-=．所以，再过65411分钟，时针与分针将第一次重合．第二次重合时显典型例题知识梳理然为12点整，所以再经过65(1210)6054651111-⨯-=分钟，时针与分针第二次重合．标准的时钟，每隔56511分钟，时针与分针重合一次．我们来熟悉一下常见钟表(机械)的构成：一般时钟的表盘大刻度有12个，即为小时数；小刻度有60个，即为分钟数．所以时针一圈需要12小时，分针一圈需要60分钟(1小时)，时针的速度为分针速度的112．如果设分针的速度为单位“l”，那么时针的速度为“112”．【小试牛刀】钟表的时针与分针在4点多少分第一次重合？【解析】此题属于追及问题，追及路程是20格，速度差是11111212-=，所以追及时间是：11920211211÷=（分）。
时钟问题可以看做是一个特殊的圆形轨道上2人追及或相遇问题，不过这里的两个“人”分别是时钟的分针和时针。
我们通常把研究时钟上时针和分针的问题称为时钟问题，其中包括时钟的快慢，时钟的周期，时钟上时针与分针所成的角度等等。
时钟问题有别于其他行程问题是因为它的速度和总路程的度量方式不再是常规的米每秒或者千米每小时，而是2个指针“每分钟走多少角度”或者“每分钟走多少小格”。
对于正常的时钟， 具体为：整个钟面为360度，上面有12个大格，每个大格为30度；60个小格，每个小格为6度。
分针速度：每分钟走1小格，每分钟走6度 时针速度：每分钟走112小格，每分钟走0.5度 注意：但是在许多时钟问题中，往往我们会遇到各种“怪钟”，或者是“坏了的钟”，它们的时针和分针每分钟走的度数会与常规的时钟不同，这就需要我们要学会对不同的问题进行独立的分析。
要把时钟问题当做行程问题来看，分针快，时针慢，所以分针与时针的问题，就是他们之间的追及问题。
另外，在解时钟的快慢问题中，要学会十字交叉法。
例如：时钟问题需要记住标准的钟，时针与分针从一次重合到下一次重合，所需时间为56511分。
【例 1】小明上午 8点要到学校上课，可是家里的闹钟早晨 6点10分就停了，他上足发条但忘了对表就急急忙忙上学去了，到学校一看还提前了10分。
中午12点放学，小明回到家一看钟才11点整。
如果小明上学、下学在路上用的时间相同，那么，他家的闹钟停了多少分？知识框架例题精讲时钟问题【巩固】—辆汽车的速度是每小时121千米，现有一块每小时快30秒的表，若用该表计时，测得这辆汽车的时速是多少?【例 2】小春有一块手表，这块表每小时比标准时间慢2分钟。
某天晚上9点整，小春将手表对准，到第二天上午手表上显示的时间是7点38分的时候，标准时间是______。
【巩固】小翔家有一个闹钟，每时比标准时间慢3分。
有一天晚上9点整，小翔对准了闹钟，他想第二天早晨7∶00起床，他应该将闹钟的铃定在几点几分？【例 3】有一个时钟每时快20秒，它在3月1日中午12时准确，下一次准确的时间是什么时间？【巩固】小明家有两个旧挂钟，一个每小时快20秒，另一个每小时慢30秒。
小学奥数钟表问题
（类似行程问题）
时钟问题主要有3大类题型：
第一类是追及问题（注意时针分针关系的时候往往有两种情况）；
第二类是相遇问题（时针分针永远不会是相遇的关系，但是
当时针分针与某一刻度夹角相等时，可以求出路程和）；
第三种就是走不准问题，这一类问题中最关键的一点：找到
表与现实时间的比例关系。
注：
1、指针速度单位：分针每分钟走6度，时针每分钟走0.5度，秒针每分钟走360度；
【例1】四点到五点之间，时钟的时针与分针在什么时刻成直角？
1、爷爷在晚上7点多出去散步，出去的时候时针与分针正好在一条直线上，
2、一只钟表的时针与分针均指在4和6
与分针的正中央，问这是什么时刻？
3、小亮晚上9点整将手表对准，他在早晨8点到校时，却迟到了10分钟，那么小明的手表每小时慢几分钟？
4、科技馆有一只奇妙的钟，一圈共有20格。
每过7分钟，指针跳一次就要跳过9个格，今天早上8点整的时候，指针恰好从0跳到9，问：昨晚8点整的时候时针指着几？
解：
昨晚8点整到今天早上8点整,12x60=720分钟
720/7=102 (6)
今天早上8点整,指针恰好从0跳到9,昨晚8点整到今天早上8点整,指针跳动103次
103x9=927
927/20=46 (7)
9-7=2
昨晚8点整的时候时针指着2。
