职高二年级第一学期数学试题

罗平县职业技术学校2016年秋季学期期末考试考试科目： 数学考试班级： 二年级1501——1511 一．选择题（本大题共20小题，每小题2分，共40分）。

1. ,,AB a AD b AC DB ===u u u r r u u u r r u u u r u u u rY 已知ABCD,+ ( ) A ．2a r B ．2b r C.2a -r D ．2b -r2. 已知A(1,3),B(5,-1),过AB 的直线的斜率与倾斜角分别是 （ ）A ． 126π，B ．14π， C ．314π-， D ．14π-，- 3.sin195=oC.14D.124.210210x y x y ++=+-=直线与的位置关系是 ( )A ．垂直 B.相交但不垂直 C.平行 D.重合5.已知点A(2,3),B(x,-3),C(3,9)在一条直线上，那么x 的值为 ( )A ．-1 B.0 C.1 D.26.已知平面向量(1,2)a =r ，(2,)b m =-r，且a r //b r ，则23a b +r r ＝（ ） A ．(5,10)-- B ．(4,8)-- C ．(3,6)-- D ．(2,4)--7. (2,3),(,6),0,a b x a b x =-=-=r r r rg已知且那么的值是（ ） A ．4 B.-1 C.9 D. -98．1,3(51)A -以点（）、B ，为端点的线段的垂直平分线的方程是 ( ) A ．340x y --= B. 340x y -+= C. 380x y -+= D. 380x y --=9.一个圆柱的高为8cm ，侧面积是48 2cm π ，则它的全面积是 ( )A ．257cm πB ．266cm πC ．266cmD ．254cm π10.两个球的体积之比是8:27,那么两个球的表面积之比为( )A ．2:3 B. 4:911.已知圆的方程为04222=+-+y x y x ，则圆心坐标和半径为（ ）A ．(1,2),5 B.(1,2),5- C.(1,2),-(1,2),12. ,10,4,,120,a b a b a b a b ===︒=r r r r r r r r g 已知向量、则 ( ) A ．20 B.20- C. 40 D. 40-13. 221y +=过坐标原点且与圆(x-2)相切的直线的斜率是( )AC.14.3cos =-),sin()523ππθθπθ<<+=已知（则 （ ）A．410--B.410-C.410-+D.410+ 15.1tan(),tan 2,tan =3αββα+==-已知则 （ ） A ．1-7B.-7C.17D.716.cos )cos(54)cos(54)sin(54)x x x x ︒+︒--︒-︒-=（36（ ）A ．0 B.1 C.1- D.217.如果圆锥的轴截面是边长为2的等边三角形，那么它的侧面积是底面积的 ( )A ．2倍B ．3倍C ．4倍D ．5倍18.若1sin cos 3αα+=，则sin2α=( )A. 1B. 89-C. -1D.8919. ,4(8)A 以点（-2）、B ，-2为直径的圆方程是( ) A ．222)(4)100x x ++-=（ B ．228)(2)100x x -++=（ C ．223)(1)100x x +++=（ D ． 223)(1)100x x -+-=（ 20.长方体的全面积为11，所有棱长之和为24，则这个长方体的一条对角线为（ ）A．5 D.6二．填空题（本大题共5小题，每小题4分，共20分）21．边长为acm 的正方体的外接球的体积为 ___ ；22．(1,(1,0),,a b a b =-=-=r r r r已知则 ；23.32)(14)80(52)(4)70a x a y a x a y a ++-+=-++-=直线（与互相垂直，则的值是 ;24.1tan151tan15+︒=-︒； 25. 22260x y x y m m ++-+=若方程表示一个圆，则的取值范围是 ___ .三．解答题（共4小题，每小题10分，共30分）。

2010-2011学年濮阳市中等职业学校第一学期二年级统考数学试题（答案）（本卷满分100分，时间100分钟）一、填空题（把正确的答案填在横线上，每小题3分，共30分）1. 在等差数列中，a l2=23，a 42=143，a n =263，则n=_________；722. 在等比数列中 那么_________ ；9,6,475==a a =9a 3．已知向量(3，－1)，(1，－2），若与垂直，则m= .a rb r b m a r r +b r －1 4. = . )64(21)2(4)32(3b a b a b a r r r r r r -+--+b a r r 144+5．已知向量︱︱=,︱︱=2，与的夹角为，则︱︱= . 1a r 3b r a r b r π6b a r r -6.两直线x-y+1=0与x+y-5=0的交点坐标为___________.(2,3)7.经过三点O(0,0),A(2,0),B(0,4)的圆的方程为________________.5)2()1(22=-+-y x 8. 在边长为a 的正方体ABCD-A 1B 1C 1D 1中，顶点A 1到底面对角线BD 的距离是__________；a 269. 在300的二面角的一个面内有一点，它到另一个面的距离是10cm ，这点到棱的距离是________.20cm10. 四条直线两两平行，其中任意三条不共面，它们可以确定_______个平面；6二、选择题（每小题只有一个正确答案，请把正确的答案的代码填在括号内，每小题3分，共30分）1．数列是等比数列的充要条件是 ( Ａ ).}{a n A. B. C. D. 常数=+n 1n a a 常数=+1n a n a 正数=+1n n a a 负数=+1n n a a2．等差数列中，已知，那么（ D}{a n 48a a a a 111032=+++=+76a a ）A ．12 B.16 C.20 D.243．为两个非零向量，其夹角为θ，那么与各自所在直线的夹角为(b a r r 、a r b r C ).A.θB.π－θC.π－θ或θD.与θ无关4. 若＜0，则与的夹角的取值范围( D ).b a r r ⋅a r b r A.[0，] B.[ ，π） C.[ ，π] D.（，π]π2π2π2π25．两条直线2x+y+a=0和x+2y-1=0的位置关系是( B )A.垂直B.相交但不垂直C.平行D.重合6. 若点M(1,3)和点N 关于C(3,7)中心对称,则点N 的坐标为( A )A.(5,11)B.(2,5)C.(1,2)D.(-1,-1))7. 空间两条互相平行的直线指的是（ D ）A.在空间没有公共点的两条直线B.分别在两个平面内的两条直线C.分别在两个不同的平面内且没有公共点的两条直线D.在同一平面内且没有公共点的两条直线8. 两条直线不平行是这两条直线是异面直线的（ B ）A 充分条件B 必要条件C 充要条件D 既不充分又不必要条件9. 三棱锥底面是正三角形为三棱锥是正三棱锥的( B )A.充分条件B.必要条件C.充要条件D.非充分,且非必要条件10.从一楼到二楼有三个楼梯可走,从二楼到三楼有两个楼梯可走,那么从一楼到三楼共有多少种走法( D )A.2B.3C.5D.6三、计算题（每小题6分，共18分）21.表示数列{}的前n 项之和，且，求数列的第8项.n S n a 2322-+=n n S n 解：∵ 2322-+=n n S n ∴1602241282838228＝－＝+-⨯+⨯=S 即数列的第8项为160.22.已知直线(a+1)x-3y-12=0与直线4x-6y+1=0平行，求a 的值。

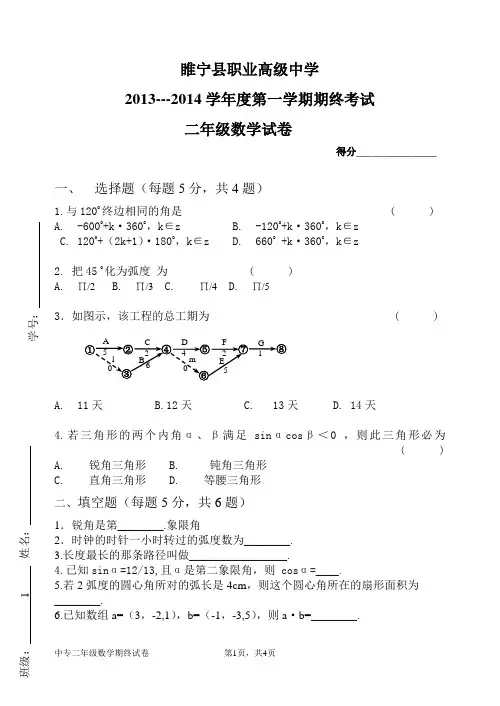
睢宁县职业高级中学2013---2014学年度第一学期期终考试二年级数学试卷得分________________一、 选择题（每题5分，共4题）1.与120o 终边相同的角是 ( )A. -600o +k ·360o ，k ∈zB. -120o +k ·360o ，k ∈zC. 120o +（2k+1）·180o ，k ∈zD. 660o +k ·360o ，k ∈z2. 把45 o 化为弧度 为 ( ) A. ∏/2 B. ∏/3 C. ∏/4 D. ∏/53．如图示，该工程的总工期为 ( )A. 11天B.12天C. 13天D. 14天4.若三角形的两个内角α、β满足sin αcos β＜0 ，则此三角形必为( )A. 锐角三角形B. 钝角三角形C. 直角三角形D. 等腰三角形 二、填空题（每题5分，共6题）1．锐角是第________.象限角2．时钟的时针一小时转过的弧度数为________. 3.长度最长的那条路径叫做_________________.4.已知sin α=12/13,且α是第二象限角，则 cos α=____.5.若2弧度的圆心角所对的弧长是4cm ，则这个圆心角所在的扇形面积为 ________.6.已知数组a=（3，-2,1），b=（-1，-3,5），则a ·b=________.1 姓名： 学号： m 0 G 1 A 5 F 2 D 4 C 2 l 0E 5 B 6 ③ ④ ⑦ ⑥ ⑧ ① ⑤ ②二、解答题（共5题，每题10分）1.已知角α的终边经过点p（1,2），求sinα，cosα，tanα2.已知公路上一段圆弧形的弯道的半径是30m，转过的圆心角是120 o，该弯道的长度是多少？3.化简cosαtanα4.填写下表中的空缺栏，并绘制相应的网络图5．小刘夫妇打算搬家，他们制定了搬家计划的工作明细（1）请填写下表中的“紧前工作”一栏搬家计划的工作明细表（2）根据工作明细表画出网络图（3）试列出从开始节点到终止节点的所有路径，并指出哪条路径是关键路径，。

2018--2019学年度第一学期期末考试试卷年级： 中专二年级 科目： 数学一、选择题（本大题共36分，每小题3分）1、已知集合}7,5,3,1,0{=A ，集合}7,5,4,2,0{=B ，则=B A （ ）A }7,5,0{B }7,5,3,1{C {}5,2,1,0D }7,5,4,3,2,1,0{2、已知135cos =x ，则=x sin ( ) A 1312 B 1312± C 1312- D 以上都不对 3、过点)5,0(，且与直线76+-=x y 平行的直线方程是（ ）A 056=++y xB 056=+-y xC 056=-+y xD 056=--y x4、不等式231≥-x 的解集是( )A )31,(--∞B ⎥⎦⎤ ⎝⎛-∞-31,C ),31(+∞-D ⎪⎭⎫⎢⎣⎡+∞-,315、在等差数列}{n a 中，52=a ，25=a ，则公差=d ( )A -1B 1C 3D -36、函数31212-++-=x xy 的定义域是( )A )1,21(-B ⎥⎦⎤ ⎝⎛-1,21C ⎥⎦⎤⎢⎣⎡-1,21D ⎪⎭⎫⎢⎣⎡-1,21 7、下列各式计算正确的是（ ）A 2223223=⋅ B 2)2(3223=⋅ C 493223222=÷ D 1)2(3223=8、=4sinπ（ ）A21 B 22 C 23 D 1 9、函数,52)(2+=x x f 则)1(-f =（ ）A 3B 5C 7D 910、已知向量)3,2(-=，)1,1(=，则=-b a 2（ ）A )1,4(-B )1,4(-C )1,4(D )1,4(--11、下列说法错误的是（ ）A 如果一个平面与两个平行平面相交，那么它们的交线互相平行B 平行于同一条直线的两条直线互相平行C 垂直于同一条直线的两条直线互相平行D 平行于同一个平面的两个平面互相平行12、要考察某地区3岁儿童的身高状况，随机抽取200个3岁儿童测身高，这200个儿童的身高是（ ）A 总体B 个体C 样本D 样本容量二、填空题：（本大题共20分，每小题4分）13、已知函数⎩⎨⎧>≤+=)0(,log )0(,1)(2x x x x x f ，则=)2(f 。

中职二年级上学期期末模拟试卷一（数学）姓名__________ 班级_________ 分数___________一、选择题（本大题共10小题，每小题3分共30分）1、数列22221111,31415161----，，，的一个通项公式为（ ）A ()2111n a n =+- B 1(2)n a n n =+C 21(2)1n a n =+- D 211n a n =- 2、在等差数列{}n a 中，若254785,9,a a a a S +=+==则（ ） A 12 B 28 C 24 D 303、等比数列{}n a 中，若135528,q a a a a ===且则（ ） A 2 B 4 C 8 D 164、化简AB AC BD CD -+-=（ ）A 2ADB 2CBC 0D 05、下列说法中不正确的是（ ） A 零向量和任何向量平行B 平面上任意三点,,,A BC 一定有AB BC AC += C 若()AB mCD m R =∈，则//AB CD D 若1122,a x e b x e ==，当12x x =时a b =6、若4,2,22a b a b =-==，则,a b =（ ） A 00 B 090 C 0120 D 01807、设()5,5,,62a m b ⎛⎫==-- ⎪⎝⎭且13,a a b =⊥，则m =（ ）A 12B 12-C 12±D 88、直线过两点((,A B -，则该直线的倾斜角是（ ） A 060 B 090 C 00 D 01809、直线230ax y +-=与直线10x y ++=互相垂直，则a 等于（ ）A 1B 2-C 23-D 13-10、以点()()1,3,5,1A B -为端点的线段的垂直平分线的方程为（ ） A 380x y -+= B 260x y --= C 340x y ++= D 1220x y ++=二、填空题（本大题共6小题，每小题4分共24分）11、在数列{}n a 中，前n 项和22n n S =+则567a a a ++=____________；12、在数列{}n a 中满足()1302n n a a n -+=≥，且13a =，则它的通项公式为____________；13、已知()()()2,2,3,4,1,5a b c =-=-=，则()3a b c -+=____________；14、已知向量()()1,,,2a x b x =-=-，且a 与b 反向共线，则x 的值为____________；15、已知直线l 与直线310x y -+=平行，且直线l 的横截距为5-，则直线l 的纵截距为____________；16、两条平行直线34206870x y x y --=-+=与的距离是____________；三、解答题（本大题共4小题，共46分）17、⑴在等差数列{}n a 中，275,20a a ==，求15S ；（5分）⑵已知等比数列{}n a 中,531,42a q ==-，求7S ；（5分）18、解答下列问题：（1) nS 是等差数列{}n a 的前n 项和，已知548=+S S ，328=-S a ，求该数列的通项公式；（6分）（2）在等比数列{}n b 中，已知1323=b b b ，且5227=b b ，求该数列的前n 项和n T .（6分）19、()1已知向量()()()1,2,3,1,21,1a b c m n =-=--=++，且,//a c b c ⊥，求实数,m n 的值；（6分） ()2已知()()21,2,1,2a m n b =+-=，且()235,5a b +=，求,a b ；（6分）20、已知直线123:210,:2330,:3470l x y l x y l x y -+=+-=-+=，直线12l l 与的交点为点P, ⑴求点P 的坐标；（6分）⑵设直线3l l 与平行且经过点P ，求直线l 的一般式方程；（6分）中职二年级上学期期末模拟试卷一参考答案二、填空题11．11212.a n=3*（-3）n-113.（-14,23）14．√215.5/316.11/10三、解答题17.(1)S15=345 (2)S7=129/16=4n-12 18.(1)an(2)Tn=1/2(3n-1) 19.(1)m=-1/2;n=-1(2)90°20.（1）P(0,1)(2)3x-4y+4=0。

1. 2. 3. 罗平县职业技术学校 2016年秋季学期期末考试考试科目: 考试班级:.选择题（本大题共 数学二年级1501——151120小题，每小题2分，共40分）。

已知匚ABCDABj j44A . 2aB . 2b已知 A(1,3),B(5,-1),A ?6sin 195二 31.呛9. 一个圆柱的高为8cm 侧面积是 A . 57二 cm 2 B . 66二 cm 210.两个球的体积之比是8:27, 48二cm 2，则它的全面积是 （）2 2C . 66 cmD . 54二 cm二 b, AC+DB 二（）C . -2a-2b过AB 勺直线的斜率与倾斜角分别是（A. 2:3A. (1,2),5B.A. 20B. B.C.D.4.直线2x 十y +1 = 0与x 十2y -1 = 0的位置关系是4:9C42 :护 D .J8 V27 2y - 2x + 4y = 0，则圆心坐标和半径为（)(1, -2),5 C .(1厂 2),V5 D . (1,2)75 10," b=4,〈爲）= 120：则妳=()-20C. 40D.-40(x-2) 2 + y 2 =1相切的直线的斜率是 ()C. 上3D .±43那么两个球的表面积之比为B.12.已知向量 a 、b, a = 13.过坐标原点且与圆() 11.已知圆的方程为x 2A.亡B——3A.垂直B. 相交但不垂直C. 平行D.重合14.已知 cos^=-?(—'),则sin( )=()5 235.已知点 A(2,3),B(x,-3),C(3,9)在一条直线上, 那么 x 的值为（）A. -1B. 0C.D. A土⑴ B. 心C.10 10-4 3 3 10D.4 3二 106.已知平面向量 a =(1,2) , b =(-2,m)，且 a// b ，则 2a 3b = 115.已知 tan (八 匸),tan- - -2,则 tan ：=3A . (-5,-10)B . (-4,-8)C . (-3,-6) (-2,-4)7.已知 a = (-2,3), b = (x, -6),且 a=0,那么x 的值是（ 1 1 A . --B.-7 C. -7716. cos(36 x)cos(54 - x)- cos(54 -B. D.x)sin(54 - x)二()A. 4B. -1C.D.-9A. 0B. 1C. -1D.8.以点A1,3）、B （-51）为端点的线段的垂直平分线的方程是17.如果圆锥的轴截面是边长为2的等边三角形，那么它的侧面积是底面积的（） A . 3x —y —4=0 B. 3x 一 y 4 二 0 C. x —3y 8 = 0 D. x —3y —8=0A. 2倍B . 3倍C . 4倍D . 5倍18.若sin :亠cos ，贝U sin2 ：=( )8 8A. 1B.C. -1D.—9 9 19. 以点A-2,4)、B(8, -2)为直径的圆方程是()2 2 2 2A • (x 2) (x-4) =100B . (x-8) (x 2) =1002 2 2 2C. (x 3) (x 1) =100 D . (x-3) (x-1) =10020. 长方体的全面积为11,所有棱长之和为24,则这个长方体的一条对角线为( ) 27.求过直线3x • 2y T= 0和直线2x- 3* 5= 0的交点，并且平行、垂直于直线6x- 2y • 5=0的直线方程。

中职高二数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. -2B. 根号2C. 0.33333（无限循环）D. 1/32. 函数f(x) = 2x^2 - 3x + 1在x=1处的导数是：A. 1B. 2C. 3D. 43. 已知等差数列的首项为5，公差为3，第10项的值是：A. 40B. 43C. 45D. 484. 圆的半径为5，圆心到直线的距离为3，则直线与圆的位置关系是：A. 相离B. 相切C. 相交D. 内切5. 已知集合A={1, 2, 3}，B={2, 3, 4}，求A∪B的结果是：A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 4}6. 以下哪个不等式是正确的？A. |-3| > -3B. |-3| < -3C. |-3| = -3D. |-3| ≤ -37. 已知三角形的两边长分别为3和4，第三边的长a满足的条件是：A. 1 < a < 7B. 0 < a < 7C. 1 ≤ a ≤ 7D. 0 ≤ a ≤ 78. 函数y = sin(x)的周期是：A. πB. 2πC. 4πD. 8π9. 以下哪个是二项式定理的展开式？A. (x+1)^2 = x^2 + 2x + 1B. (x-1)^2 = x^2 - 2x + 1C. (x+1)^3 = x^3 + 3x^2 + 3x + 1D. 以上都是10. 已知向量a=(3, 4)，b=(-1, 2)，向量a与b的点积是：A. 10B. 8C. 6D. 2二、填空题（每题4分，共20分）11. 已知等比数列的首项为2，公比为2，第5项的值是______。

12. 函数f(x) = x^3 - 3x^2 + 2的极小值点是x = ______。

13. 已知三角形ABC，AB=5，AC=7，BC=6，根据余弦定理，角A的余弦值为______。

中职高二上册数学练习题一、选择题1. 已知函数 f(x) = 2x - 5，求 f(3) 的值是多少？A) 1B) 3C) 4D) 62. 若 2x + 5 = 11，求 x 的值为多少？A) -3B) -2C) 2D) 33. 某物品原价为 120 元，现以八折出售，求出售后的价格是多少？A) 24 元B) 60 元C) 90 元D) 96 元4. 一个正方形的边长为 x 米，求该正方形的面积是多少？A) xB) 2xC) x²D) 2x²5. 若 a:b = 3:4，且 b = 20，求 a 的值为多少？A) 5B) 10C) 15D) 25二、填空题1. 下面哪个数字是素数：（ 2 ）2. 若 a + 3 = 7，求 a 的值为：（ 4 ）3. 若一个圆的半径为 5cm，其直径是多少 cm：（ 10 ）4. 若 x + 5 = 8，求 x 的值为：（ 3 ）5. 下面哪个数字是偶数：（ 16 ）三、解答题1. 请计算下列等式的结果：(a) 2³ + 4 - 5 × 2(b) 3 × 4² + 8 ÷ 2 - 52. 请解决以下方程：(a) 2x + 3 = 9(b) 5(2x - 3) = 253. 一个矩形的长比宽大 5，且周长等于 70，求该矩形的长和宽各是多少？四、证明题证明：三角形内角和是180度。

解答：设三角形的三个内角分别为 A、B、C。

根据三角形的性质，三个内角之和等于180度，即 A + B + C = 180。

所以，我们证明了三角形内角和是180度。

五、应用题某电商平台举办了一次促销活动，某商品原价为150元，促销期间价格降低20%。

1. 请计算促销期间该商品的实际售价是多少？2. 若一位顾客购买了该商品5件，他总共支付了多少钱？3. 若该顾客支付了200元，他购买的商品数量是多少件？六、综合题1. 一块蛋糕被4人分享，每人分得的蛋糕重量是250克。

中职高二上数学复习测试题一、单项选择题1.函数y ＝2＋sinx 的最小正周期是（ ）A.πB.2πC.3πD.4π2.函数y ＝sinx 的定义域是（ ）A.（－1，1）B.RC.∅D.（0，2π）3.函数y ＝sinx 在[0，π]上的最大值为（ ）A.－1B.0C.1D.24.函数y ＝－5sinx 的最小正周期是（ ）A.πB.2πC.3πD.4π5.下列关于函数y ＝sinx 的叙述，正确的是（）A.在⎣⎢⎡⎦⎥⎤0，π2上单调递增B.函数图象关于y 轴对称C.在⎣⎢⎡⎦⎥⎤0，π2上单调递减 D.值域为R6.若函数y ＝asinωx 的最大值为2 020，则a 的值为（ ）A.2 020B.－2 020C.2 020或－2 020D.无法确定7.函数y ＝1－sin π23x ⎛⎫+ ⎪⎝⎭的最小正周期和最大值分别是（）A.π2，1B.π2，2C.π，2D.π，08.求值：2tan22.5°1－tan222.5°等于（ ） A. 3 B.－ 3 C.1 D.－19.以下公式正确的是（ ）A.sin （α＋β）＝sin αcos β＋cos αsin βB.cos （α＋β）＝sin αcos β＋cos αsin βC.sin （α－β）＝sin αcos β＋cos αsin βD.cos （α－β）＝sin αcos β＋cos αsin β10.sin85°cos25°－cos85°sin25°＝（ ）A.12B.C.2D.－2二、填空题11.求值：sin19°cos79°－sin71°cos11°＝ .12.求值：1－2sin2π12＝ .13.函数F （x ）＝3sin4x －4cos4x 的最大值为 ，最小正周期为 .14.若sin （π＋α）=13，且α是第四象限角，则tan α= .15.计算：sin15°cos15°cos30°＝ .16.计算：＝ .17.函数y ＝lg （2sin x ＋ 3 ）的定义域为 .18.若2sinα－4cos α＝0，则tan 2α＝ .19.若集合A ＝{y|y ＝sin x}，则自然数集Ν∩A ＝ .20.函数y ＝1sin 2x ＋1的定义域为 . 三、解答题21.已知tanα＝12，求tan2α的值.22.已知f（x）＝asinx（a≠0），且f（2）＝4，求f（2π－2）的值.23.求函数f（x）＝2sinxcosx＋1－2sin2x的最小正周期和值域.24.求函数y＝3＋2sinx（x∈R）的值域.25.若sinx＋32a-＝0，求a的取值范围.26.已知函数f（x cos2x sin2x＋sin2x.求：（1）函数f（x）的最小正周期；（2）函数f（x）的最大值以及取得最大值时x的值.27.已知sinα＝45，α为锐角，求sin2α＋cos2α的值.28.已知cosθ＝－35，且θ∈3ππ2⎛⎫⎪⎝⎭，，求cos2θ和tan2θ的值.29.已知角α的终边是一次函数y＝2x（x≥0）所表示的曲线，求sin2α.30.已知sinα＝35，α∈（π2，π），tan（π－β）＝12，求tan（α－2β）的值.答案一、单项选择题1.B2.B3.C4.B5.A6.C7.C 【提示】T ＝2πω＝π，ymax ＝1－（－1）＝2.8.C 【解析】原式＝2tan22.5°1－tan222.5°＝tan45°＝1. 9.A 【提示】由两角和的公式可知A 选项正确，故选A.10.B 【提示】sin85°cos25°－cos85°sin25°＝sin （85°－25°）＝sin60°B.二、填空题11.－32 12.3213.5 π214.－24sin15°cos15°cos30°＝12sin30°·cos30°＝14sin60°16.cos10sin10︒+︒ cos20cos10sin10︒==︒-︒22cos 10sin 10cos10sin10︒-︒︒-︒ cos10sin10=︒+︒.17.4|22,33x k x k k Z ππππ⎧⎫-+<<+∈⎨⎬⎭⎩ 【提示】由题意得2sin x ＋ 3 >0，∴sin x>－32 ，根据函数图像得－π3 ＋2kπ<x<4π3 ＋2kπ，k ∈Z18.－43 【提示】tan 2α＝2tan α1－tan2α ＝2×21－22＝－43 . 19.{0，1} 【提示】A ＝{y|y ＝sin x}＝{y|－1≤y≤1}，N∩A ＝{0，1}． 20.3,4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭【提示】∵y ＝1sin 2x ＋1，∴sin 2x≠－1，解得x≠3π4 ＋kπ(k ∈Z)，∴定义域为3,4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭. 三、解答题 21.解：tan 2α＝2tanα1－tan2α＝2122112⨯⎛⎫- ⎪⎝⎭＝43.22.解：∵f （2）＝asin2＝4，f （2π－2）＝－f （2）＝－asin2＝－4.23.解：f （x ）＝sin2x ＋cos2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4， ∴T ＝2π2＝π，值域为[－2，2].24.解：∵sinx ∈[－1，1]，∴2sinx ∈[－2，2]，∴3＋2sinx ∈[1，5]．25.解：sinx ＝32a-，∵sinx ∈[－1，1]，∴a ∈[1，5]．26.【解】因为f （x＋sin2x ＝2sin （2x ＋π3）.（1）T ＝π；（2）因为2x ＋π3＝π2＋2kπ，k ∈Z ，所以当x ＝π12＋kπ，k ∈Z 时y最大值为2.27.解：本题考查同角三角函数的平方关系及二倍角公式.∵α为锐角，∴cos α＝35，∴sin2α＝2sinαcos α＝2×45×35＝2425，cos 2α＝cos 2α－sin2α＝925－1625＝－725.∴sin2α＋cos 2α＝1725.28.解：二倍角公式的逆用，即降次扩角公式的应用. 2cos 2θ＝1cos 2θ+＝15，sin2θ2＝1cos 2θ-＝45.∵θ∈3ππ2⎛⎫ ⎪⎝⎭，，∴2θ∈π3π24⎛⎫ ⎪⎝⎭，， ∴cos 2θ＜0，sin 2θ＞0， ∴cos 2θ＝－55，sin 2θ＝255，tan 2θ＝－2. 29.解：在角α的终边y ＝2x （x ≥0）上取一点P （1，2），sinα＝212＋22＝255，cosα＝112＋22＝55． ∴sin2α＝2sinα·cosα＝45．30.【解】∵sinα＝35，sin2α＋cos2α＝1，∴cos2α＝1625，又∵ππ2α⎛⎫∈ ⎪⎝⎭，，∴cos α＝45-，tanα＝34-.tan （π－β）＝－tan β＝12，tan2β＝22tan 431tan ββ=--.。

职业高中高二上学期期末考试数学试题卷一、选择题（每小题3分，共30分。

每小题中只有一个选项是正确的）1.已知B(-2,5),且()3,3=,则点A 的坐标为 ( ) A.(-5,2) B.(5,2-) C.(1,8) D.(1,2)2.已知||=5，()3,-=k ，则k 的值是 ( ) A.4- B.4 C. 4± D.2-3.已知BC AD 31=,则四边形是 ( )A.平行四边形B.矩形C.梯形D.对边不平行的四边形4.在边长为2的等边△ABC 中,∙= ( ) A.4 B.-4 C.2 D.2-5.已知+=0的 ( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件6.直线0133=-+y x 的倾斜角是 ( )A.030B.0150C.060D.01207.直线0643=+-y x 与圆()()43222=-+-y x 的位置关系是 ( )Ａ.过圆心 Ｂ.相切 Ｃ.相离 Ｄ.相交且不过圆心8.正方体棱长为a ，则其对角线长为 ( ) A.a 3 B.a 3 C.a 2 D.2a9.空间中垂直于同一直线的两条直线的位置关系是 ( ) A.平行 B.相交 C.异面 D.以上均有可能10. 如果二面角的一个面上的点到棱的距离是它到另一个面的距离的3倍，那么这个二面角的平面角θ应该满足 （ ）A .030=θB . 060=θ C . 33sin =θ D . 33cos =θ 二、填空题（每小题3分，共24分）1.已知向量与反向==6,则= 2.在菱形ABCD 中,()()=-∙+ 3.已知=(2,1),=(3,m ),且∥,则实数m =4.若直线的斜率为2，且过点()2,1-，则直线的方程为5.已知点A ()5,2-和B ()5,6-，以AB 为直径的圆的标准方程为6. 直线4=+y ax 与014=-+ay x 互相垂直，则=a7.如果直线m ⊥n ,且m ⊥平面α，则n 与平面α的关系为 8.将正方形ABCD 沿AC 折成直二面角后=∠DAB 三、计算题（每小题6分，共24分）1.已知()m ,5=，()1,3-=，且-3与+互相垂直，求m 的值。

2010-2011学年度第一学期期末考试职高二年级数学试卷说明：1、考试范围：《直线和圆的方程》、《立体几何》、。

2、考试时间：100分钟，满分：100分。

3、所有答案均需写在答题卷上，考试结束只收答题卷。

一、选择题（每小题3分, 共30分. 每小题只有一个选项是正确的, 请将正确选项的序号填在题后的括号内)1．点（-1，2）到直线x+2y+1=0的距离是（ ）A ．554B ． 55C ．334D ．332．已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行，则m 的值为 （ ）A ． -8B ．0C ．2D ．103．一条直线和这条直线外不共线的三个点，能够确定的平面个数是 （ ） A ．一个B ．三个C ．四个D ．一个或三个或四个4．异面直线是 （ ） A ．分别位于两个不同的平面的两条直线 B ．空间不相交的两条直线C ．空间不平行的两条直线D ．不同在任何一个平面内的两条直线5. 直线x-y+1=0与2x+y+5=0的位置关系是（ ）. A ．相交 B ．平行 C ．垂直 D ．重合6． 已知空间四边形两条对角线相等，则依次连接各边中点所成的四边形是（ ） A ．空间四边形B ．矩形C ．正方形D ．菱形7．两不重合的平面与同一直线所成的角相等，则这两平面的位置关系是（ ） A ．平行 B ．相交 C ．平行或相交 D ．以上结论都不对8．方程x 2+y 2-mx+1=0表示圆，则m 的取值范围是．（ ） A ．m ＜-2或m ＞2 B ．-2＜m ＜2C ． -4＜m ＜4D ．m ＜-4或m ＞49．已知二面角α－l －β内一点P 到二面角的两个面α、β的距离分别为PA 、PB ，且PA=PB=AB=2，则二面角的度数是 （ ） A ．60 B ．120 C ．60120 或 D ．15010．在棱长为1的正方体ABCD-A 1B 1C 1D 1中，点A 到B 1D 1的距离是 （ ） A ．36 B ．26 C ．46 D ．56二、判断题（每小题1分,共10分. 正确的，在题后括号内打“√ ”，错误的打“×”) 11．在数轴上的点离原点越远，表示的数越大. （ ） 12．任意一条直线都存在唯一的倾斜角，但不一定都存在低斜率. （ ） 13．如果两条直线平行，那么它们的斜率一定相等或都不存在. （ ） 14．若A ，B 是圆C 外两点，则直线AB 与圆C 相离. （ ） 15．直线3x+4y-5=0与圆(x-2)2+y 2=16相交. （ ） 16．两条相交直线可以确定一个平面. （ ） 17．如果一个平面内有无数条直线与另一平面平行，则这两个平面平行.（ ） 18．不重合的两条直线既不相交也不平行，则这两条直线一定是异面直线.（ ） 19．若,,.m a m a αβα=//// 且则. （ ） 20．一条直线与平面的斜线在平面内的射影垂直，就与这条直线垂直.（ ）三、填空题（每小题3分, 共30分)21．若点A(3，m)与点B(0,4)的距离为5，则m ＝________. 22．过点（2，3）且垂直于x 轴的直线方程为_____________.23．倾斜角是135°,在y 轴上的截距是3的直线方程是___________________. 24．两平行直线3x-y+1=0与6x-2y-8=0间的距离为_______.25．以C(1,2)为圆心，且与直线5x-12y-7=0相切的圆的标准方程是_____________. 26．两个平面最多可把空间分成 部分.27．球心到截面圆心的距离为3，球半径为5，则截面圆直径为____________.28．如图，正方体ABCD —A 1B 1C 1D 1中，E ，F 是棱AA 1和A 1B 1的中点，则EF 与BD 所成的角为 .29．由长方体的一个顶点出发的三条棱长为1，2，3，则其对角线长为 .30．若二面角α－l －β为60，A ∈平面α，点A 到棱l 的距离为2，则点A 到平面β的距离为 .四、解答题（31、32题每小题7分,33、34题每题8分， 共30分）31．已知点P(-1,3),Q(5,1)，求线段PQ 的垂直平分线的方程.32.已知△ABC 中，A(0,0),B(2,0),C(2,4),求△ABC 的外接圆的方程.33．已知,A B 是直二面角l αβ--的棱上两点, 线段AC α⊂, 线段BD β⊂, 且AC l ⊥, BD l ⊥, 6AC AB ==, BD=3, 求线段CD 的长.lαβCDAB34. 已知：正方体ABCD —A 1B 1C 1D 1中，E 是DD 1的中点，求证:D 1B//平面ACEEA BB 1D 1C 1A 1DCFEA BB 1D 1C 1A 1DC2010-2011学年度第一学期期末考试职高二年级数学参考答案一、选择题（每小题3分, 共30分. 每小题只有一个选项是正确的, 请将正确选项的序号填在题后的括号内)题号 1 2 3 4 5 6 7 8 9 10 答案 A A D D A D C A B B二、判断题（每小题1分,共10分. 正确的，在题后括号内打“√”，错误的打“×”)题号11 12 13 14 15 16 17 18 19 20 答案×√√×√√×√××三、填空题（每小题3分, 共30分)1021.0或8 22.x=2 23.y=-x+3 24.225.(x-1)2+(y-2)2=4 26.4 27.828.60○ 29.1430.3四、解答题（31、32题每小题7分,33、34题每题8分，共30分）31.3x-y-4=032.x2+y2-2x-4y=033.934.略。

中等职业学校公共基础课水平测试数学测试试卷（满分：100分;时间：90分钟)1.用列举法表示不等式+27x≤的所有正奇数的解集是{1,3}. （）2.设全集U={2,1,16,1,0}-，A={1,2,16}-，则={1,0}UAð. （）3.不等式||x≤1的解集为(1,1)-. （）4.区间(5,0]-可用集合表示为{|50}x x-<<. （）5.若53,x+<-则8x>-. （）6.已知()f x=(4)3f=. （）7.3()1f x x=-在R上是减函数. （）8.函数21()+1f xx=的定义域为R. （）9.2logy x=的图像过点(1,0). ( )10.把对数式ln3x=写成指数式是3x e=. （）11.22231log+log384=. （）12.函数xy=是指数函数. （）13.指数函数都是非奇非偶函数. （）14.=303π︒. （）15.30060︒︒与是终边相同的角. （）16.96-︒是第二象限角. （）17.角α的终边与单位圆的交点坐标为34(,)55-，则角α的余弦值为35-. （）18.已知1cos2α=-，且α是第二象限角，则tanα的值是. （）19.cos1080︒>. （）20.sin0︒的值等于1. （）21.当sinα时，=45α︒. （）22.sin360︒的值等于1. （）23.1是等比数列{3}n的项. （）24.数列1,2,3,4----与数列4,3,2,1----是相同的数列. （）25.数列1,1,1,1,1,,---的通项公式为1(1)nna+=-. （）26.等差数列1,2,3,4，的前7项和为28. （）27.等比数列1,3,9,27--，的前5项和为60. （）28.(0,2),(0,3)a b==-，a与b是共线向量. （）29.+0AB BD DA+=. （）30.直线3y x=+与直线23y x=+的交点坐标为(0,3). （）31.直线5y x=-+与直线+3=0x y-的位置关系为平行. （）32.直线30x y--=的斜截式方程是+3y x=-. （）一、判断题（每题1分，共40 分）学校______________________姓名:______________学籍号:_________________年级:______________专业:_____________…….…………………………….密…………………………………封…………………………………线……………………………………第1 页共8页第2 页共8页第4 页共8页33.斜率不存在为的直线的倾斜角为90︒. （）34.平行于同一条直线的两直线互相平行. （）35.垂直于同一个平面的两直线平行. （）36.圆柱的母线平行且相等，且等于圆柱的高. （）37.底面是正方形的四棱锥一定是正四棱锥. （）38.从1,2,3,45，这五个数中任取一个，得到奇数的概率是35. （）39.由12,3,4，可组成24个可以重复数字的四位数. （）40.抛掷两次骰子，则两次都出现偶数点的概率是14. （）1.设{}{}2,1,1,1,1,2A B=-=-，则A B=（）A. {}1,1,2- B. {}1- C. {}1 D. {}22.指出条件p是结论q的什么条件？条件:20p x+=，结论:(2)(5)0q x x++=.（）A. 必要条件B. 充分条件C. 充分且必要条件D. 不确定3.不等式10x->的解集为（）A. []1,1- B. (1,1)- C. (,1)(1,)-∞-+∞ D. (,1][1,)-∞-+∞4.不等式(2)(3)0x x--<的解集为（）A. (,2)(3,)-∞-+∞ B. (,2)(3,)-∞+∞ C. (2,3)- D. (2,3)5.已知()tanf x x=，则()4fπ的值为（）A.3B.2C. 1D.6.函数()f x=的定义域为（）A. (,1]-∞ B. (,0]-∞ C. (,0)(0,)-∞+∞ D. R7.函数()f x x=是（）.A.奇函数B. 偶函数C. 非奇非偶函数D. 既奇又偶函数8.函数()43f x x=+在R上是（.）A. 减函数B. 增函数C. 先增后减D. 先减后增9.函数1yx=的图像不过（）A. 原点B. (1,1)C. (1,1)-- D. 无法确定10.如果21log log32a a>，则a的取值范围是（）A. )1,0(B. )0,(-∞ C. ),0(+∞ D. ),1(+∞11.把指数式124x⎛⎫=⎪⎝⎭化为对数式为（）A.1log24x= B.21log4x= C.14log2x= D.14log2x=12.函数3y x=的图像关于（）对称. （）A. x轴B. y轴C. (0,0)D. 直线y x=13.把指数幂23a化成根式的形式是（）A. aB.C.D.14.计算63a a÷=（）A. 9aB. 6aC. 3aD. 2a二、单选题：（每题1分，共40分）专业:_____________………………………第3 页共8页第5 页 共8页 第6 页 共8页15.下列函数属于指数函数的是 （ ）A. 0.3xy =- B. 0.3xy = C. 0.3y x = D. 22y x -=16.53π是 （ ） A. 第一象限角 B.第二象限角 C.第三象限角 D. 第四象限角17. 在0~360之间，与60-终边相同的角是 （ ） A. 660 B.320 C.390 D. 30018. 1的弧度数是 （ ） A. 1 B.2π C. 3πD. 180π19.函数2cos21y x =-+的最小值是 （ ） A. 2 B. 2- C. 1- D. 320. 已知角α的终边经过点(3,0)，则角α的正弦值为 （ ） A.31B. 0C. 3D. 1 21. tan(315)-= （ ）A. 3B. 1C. 1-D. 2122. 108的各三角函数值的符号为 （ ） A. sin 0α> B. 0cos >α C. 0tan <α D. 以上都不对23. sin 270等于 （ ） A. 0 B. 1- C. 1 D.1224. 数列 ,8,6,4,2的第8项是 （ ） A. 16 B. 17 C. 18 D. 1925. 24是数列 ,15,12,9,6,3的第几项？ （ ）A. 8B. 9C. 10D. 11 26. 等差数列2,6,10,14,的通项公式是 （ ）A. 42n a n =+B. 46n a n =-C. 42n a n =-D. 24n a n =- 27. 等比数列1111,,,,392781的通项公式是 （ ）A. n n a 31=B. n n a 31-=C. 21+-=n a nD. na n +-=3128. (1,2),(3,1),a b =-=-则a b ⋅= （ ）A. 5B. 5-C. 1-D. 129. 下列等式错误的是 （ ） A. a b b a +=+ B. 00a a +=+ C. ()0a a +-= D. ()=0+-a a 30. 点(2,1)P -到直线230x y -=的距离为 （ ）A.B.C.D. 31. 关于直线1x =与直线7y =说法正确的是 （ ） A. 垂直 B. 平行 C. 重合 D. 无法确定32. 直线1y =与直线1=x 的交点坐标为 （ ） A. )1,1(- B. )1,2( C. )2,1( D. (1,1)33. 若点(1,2)A 与点B 关于点(2,5)P 对称，则点B 的坐标为 （ ） A. (3,8) B. (1,8)- C. (1,1)- D. (0,1)-34. 圆224x y +=的圆心为 （ ） A. (1,0) B. (0,0) C. (0,1) D. (0,2)35. 方程2226100x y x y ++-+=表示 （ ）第7 页 共8页 第8 页 共8页A.圆B. 不表示任何图形C. 点D. 无法确定 36. 平面的斜线与平面所成角的范围是（ ）A. (0,90)B. (0,90]C. (0,180)D. ]90,0[37.过两条平行直线中的一条，可做多少个平面平行于另一条直线？ ( ) A. 一个 B. 两个 C. 三个 D. 无数个38. 某学校高一年级共有7个班，高二年级6个班，从中选一个班级担任学校星期一早晨升旗任务，共有( )种安排方法.A. 14B. 13C. 12D. 4239. 在随机试验中，对于不可能事件φ，则()P φ= ( ) A. 等于1 B. 等于0 C. 大于0 D. 大于等于0且小于等于1 40. 抛掷一颗骰子，“出现偶数点”的事件是 ( ) A. 必然事件 B. 不可能事件 C. 基本事件 D. 随机事件1.表示所有大于7的整数组成的集合是 （ ） A.{}Z x x x ∈>,7 B.{} ,10,9,8 C.{}Q x x x ∈>,7 D.{}7>x 2.已知集合{}{}60,52≤≤=<<-=x x B x x A ，则=⋂B A （ ） A.[0,5) B.(2,6]- C. {}05x x ≤< D. {}26x x -<≤ 3. 下列函数定义域为(),0-∞的是 （ ） A.y =B.2log ()y x =-C. y =D. y =4.下列对数值大于零的是 （ ） A.ln e B. ln 5 C. 1ln 2D .ln 0.6 5. 已知4sin 5∂=，则∂tan 的值可能是 （ ） A ．35- B. 35 C.34 D.34-6.以下哪些数是数列{(1)n +- 的项 （ ）A.1B.2C.3D.47.5a →=，且(,4)a k →=- ，则=k （ ） A.3 B. -3 C.4 D.-48.圆心在原点，的圆的标准方程错误的是 （ ） A ．224x y += B.224x y -= C. 222x y += D. 222x y -= 9.两个平面可以把空间分成 （ ）A.两部分B.三部分C.四部分D.五部分10.从甲、乙、丙、丁四人中挑选1人去参加职业技能大赛。

2011-2012学年第一学期期末考试职高二年级数学试题命题人：李淑艺注意事项：1、本试卷共三道大题，共120分2、答题一律用蓝黑钢笔或圆珠笔答在答题纸上，交卷时只交答题纸3、时间为120分钟4、考生将自己的姓名、准考证号、所在班级写在答题纸上，考生须将答案写在答题纸对应题目的后面，写在试题卷上无效。

一， 单项选择题（本题有15个小题，每题3分，共45分）1、以C （2，－1）为圆心，半径为4的圆的标准方程是（ ） A (x －2)2+（y+1）2=16 B (x +2)2+（y －1）2=16 C (x －2)2+（y+1）2=4 D (x +2)2+（y －1）2=42、圆x 2+y 2+8x －2y －8=0的圆心坐标、半径分别为（ ）A (4，－1)， 3B (－4， 1) , 5 C(4， 1), 5 D(－4， 1), 9 3、如图所示，方程y=21x 的曲线（ ）4、圆心为（2，－3），且与y 轴相切的圆的方程为（ ） A (x －2)2+（y+3）2=4 B (x －2)2+（y －3）2=4 C (x －2)2+（y+3）2=9 D (x －2)2+（y －3）2=9’5、直线y=3x 与圆(x －4)2+y 2=4 的位置关系是（ ）A 相切B 相离C 相交且过圆心D 相交不过圆心 6、空间四点中，三点共线是四点共面的（ ）A 充分条件B 必要条件C 充要条件D 既不充分也不必要条件 7、没有公共点的两条直线的位置关系是（ ）A 平行B 异面C 平行或异面D 相交或异面8、已知空间四边形的两条对角线相等，则依次连接各边中点所成的四边形是（ ）A 平行四边形B 矩形C 正方形D 菱形9已知P 是平面ABC 外一点，且PA=PB=PC,PH ⊥平面ABC 于H ，则垂足H 是△ABC 的（ ） A 外心 B 内心 C 重心 D 垂心10、线段AB 的长等于它在平面α上射影的2倍，则AB 所在直线和平面α所成的角为 （ ） A 300 B 120 0 C 60 0 D 45 011、△ABC 中，AB=AC=5，BC=6，PA ⊥平面ABC,PA=8，则P 到BC 的距离是（ ） A 45 B 35 C 25 D512、正六棱锥的底面边长为a ，体积为323a 则侧棱与底面所成的角为（ ） A 300 B 60 0 C 45 0 D 90013、某乐队有11名乐师，其中男乐师7人，现该乐队要选出一名指挥，则选出的指挥为女乐师的概率为（ ） A117 B 41 C 74 D 114 14、下列现象中，不是随机现象的有（ ） Ａ 买一张奖券中奖 Ｂ 明天下雪Ｃ 太阳从东方升起 Ｄ 从装有６个白球４个红球的袋中任取一球，取出红球 15、将3封不同的信逐一投入到4个不同的邮筒中，则每个邮筒中至多有一封信的概率是（ ） A165 B 167 C 83 D 85 二、填空题（本大题共15空，每空2分，共30分）16、圆(x －a)2+（y －b ）2=r 2过原点的充要条件是17、圆心为（1，－2），半径为25的圆在x 轴上截得弦长是18、(x －1)2+（y+1）2=4的圆心到直线x+y+2=0的距离为 此时直线与圆的位置关系为19、空间中垂直于同一条直线的两条直线的位置关系为20、正三棱锥的底面边长为3cm ，高是1cm ，那么它的侧棱长是 ，侧棱与底面所成的角是 体积是 21、 把等腰三角形ABC 沿斜边BC 上的高线AD 折成一个二面角，此时∠BAC= 60 0，那么此二面角的大小为22、在正方体ABCD---A 1B 1C 1D 1中,∠A 1B C 1= ,与AC 1成异面直线的棱有23、由 0,1,2,3,4,5可以组成 个无重复数字的三位数，可以组成 个无重复数字的三为偶数。

职高高二第一学期数学期末考试试卷班级 姓名 学号 得分一、选择题(共12小题，每小题3分，共36分。

在每小题列出的四个选项中，只有一项是符合题目要求．．．．．．．．．．．的．) 1、圆0222=+++y x y x 的圆心坐标和半径分别是( ) .A 45),1,21( .B 45),1,21(-- .C 25),1,21( .D 25),1,21(-- 2、设线段AB 的中点为M,且A ( -4 , 0 ) , B (7 , -2 ) ，则点M 的坐标为 ( ).A 、)1,211(-B 、)1,23(-C 、)1,211(-D 、)1,23(- 3、设直线m ∥平面a ，直线n 在a 内，则 ( ).A ．m ∥nB ．m 与n 相交C ．m 与n 异面D ．m 与n 平行或异面4、平行于x 轴，且过点（3,2）的直线方程为（ ）.A.3=xB.2=yC.x y 23=D.x y 32= 5、如果 a 、b 是异面直线，那么与 a 、b 都平行的平面（ ）A ．有且只有一个B ．有两个C ．有无数个D ．不一定存在6、过空间一点，与已知直线平行的平面有（ ）A ．1个B ．2个C ．3个D 无数个7、半径为3且与y 轴相切于原点的圆的方程为（ ）.A 、()93-22=+y xB 、()9322=++y x C 、()9322=++y x D 、()93-22=+y x 或()9322=++y x 8、点（5,7）到直线01-34=-y x 的距离=（ ）.A 、252B 、58C 、8D 、52 9、都与第三个平面垂直的两个平面（ ）A.互相垂直B.互相平行C.相交D.如果相交，那么交线垂直于第三个平面10、已知直线L 1：13+=x y 与直线L 2：01=++y ax ，若L 1⊥L 2，则a=（ ）.A 、31- B 、31 C 、3- D 、3 11、空间中垂直于同一条直线的两条直线（ ）A.互相平行B.互相垂直C.异面或相交D.平行或异面或相交12、直线x y 3-=与圆()44-22=+y x 的位置关系是（ ）. A 、相切 B 、相离 C 、相交且过圆心 D 、相交不过圆心第14题 二、填空题（每空格3分，共18分。

职高高二数学练习题及答案题一：已知函数 f(x) = x^2 + 2x - 3，求解以下问题：1. 求函数的定义域；2. 求函数的值域；3. 求函数的图像在坐标平面上的顶点坐标。

解答：1. 函数的定义域表示 x 可取的值的范围。

对于 f(x) = x^2 + 2x - 3，由于二次函数对于任意实数值的 x 都有定义，所以函数的定义域为全体实数集（即 R）。

2. 函数的值域表示函数所有可能取到的值的范围。

由于函数 f(x) 是一个二次函数，开口向上，所以它的值域是大于等于它的最低点的纵坐标值。

为了确定最低点的纵坐标，可以求函数的导数，令导数为零，即求函数的极小值点。

对 f(x) 求导得 f'(x) = 2x + 2。

令 f'(x) = 0，解得 x = -1。

将 x = -1 代入 f(x) 得到 f(-1) = (-1)^2 + 2(-1) - 3 = -4。

因此，函数的最低点为 (-1, -4)。

因此，函数的值域为大于等于 -4 的所有实数，即值域为 (-4, +∞)。

3. 为了求函数的顶点坐标，可以利用二次函数的顶点公式。

顶点公式为 x = -b / (2a)。

对于 f(x) = x^2 + 2x - 3，a = 1，b = 2，所以顶点坐标为 x = -2 / (2* 1) = -1。

将 x = -1 代入 f(x) 得到 f(-1) = (-1)^2 + 2(-1) - 3 = -4。

因此，函数图像在坐标平面上的顶点坐标为 (-1, -4)。

题二：一辆汽车以每小时 60 公里的速度行驶，求解以下问题：1. 该车在 5 小时内行驶的距离；2. 该车以每小时 60 英里的速度行驶时，5 小时内行驶的距离。

解答：1. 该车以每小时 60 公里的速度行驶，则它每小时行驶 60 公里。

在5 小时内，它行驶的总距离为 60 公里/小时 × 5 小时 = 300 公里。

2. 如果该车以每小时 60 英里的速度行驶，则它每小时行驶 60 英里。

2011-2012学年第一学期期末考试职高二年级数学试题命题人：李淑艺注意事项：1、本试卷共三道大题，共120分2、答题一律用蓝黑钢笔或圆珠笔答在答题纸上，交卷时只交答题纸3、时间为120分钟4、考生将自己的姓名、准考证号、所在班级写在答题纸上，考生须将答案写在答题纸对应题目的后面，写在试题卷上无效。

一，单项选择题（本题有15个小题，每题3分，共45分）1、以C（2，－1）为圆心，半径为4的圆的标准方程是（）A(x－2)2+（y+1）2=16 B (x+2)2+（y－1）2=16C (x－2)2+（y+1）2=4D (x+2)2+（y－1）2=42、圆x2+y2+8x－2y－8=0的圆心坐标、半径分别为（）A(4，－1)， 3 B (－4， 1) , 5 C(4， 1), 5 D(－4， 1), 93、如图所示，方程y=21x-的曲线（）4、圆心为（2，－3），且与y轴相切的圆的方程为（）A(x－2)2+（y+3）2=4 B (x－2)2+（y－3）2=4C (x－2)2+（y+3）2=9D (x－2)2+（y－3）2=9’5、直线y=3x与圆(x－4)2+y2=4的位置关系是（）A相切 B 相离 C 相交且过圆心 D 相交不过圆心6、空间四点中，三点共线是四点共面的（）A充分条件B 必要条件 C 充要条件D既不充分也不必要条件7、没有公共点的两条直线的位置关系是（）A平行 B 异面 C 平行或异面 D 相交或异面8、已知空间四边形的两条对角线相等，则依次连接各边中点所成的四边形是（）A平行四边形 B 矩形 C 正方形 D 菱形9已知P是平面ABC外一点，且PA=PB=PC,PH⊥平面ABC于H，则垂足H是△ABC的（）A外心 B 内心 C 重心 D 垂心10、线段AB的长等于它在平面α上射影的2倍，则AB所在直线和平面α所成的角为（）A 300 B 120 0 C 60 0 D 45 011、△ABC中，AB=AC=5，BC=6，PA⊥平面ABC,PA=8，则P到BC的距离是（）A45 B 35 C 25 D 512、正六棱锥的底面边长为a，体积为323a则侧棱与底面所成的角为（）A300 B 60 0 C 45 0 D 90013、某乐队有11名乐师，其中男乐师7人，现该乐队要选出一名指挥，则选出的指挥为女乐师的概率为（）A117B41C74D11414、下列现象中，不是随机现象的有（）Ａ买一张奖券中奖Ｂ明天下雪Ｃ太阳从东方升起Ｄ从装有６个白球４个红球的袋中任取一球，取出红球15、将3封不同的信逐一投入到4个不同的邮筒中，则每个邮筒中至多有一封信的概率是（）A165B167C83D85二、填空题（本大题共15空，每空2分，共30分）16、圆(x－a)2+（y－b）2=r2过原点的充要条件是17、圆心为（1，－2），半径为25的圆在x轴上截得弦长是18、(x－1)2+（y+1）2=4的圆心到直线x+y+2=0的距离为此时直线与圆的位置关系为19、空间中垂直于同一条直线的两条直线的位置关系为20、正三棱锥的底面边长为3cm，高是1cm，那么它的侧棱长是，侧棱与底面所成的角是体积是21、把等腰三角形ABC沿斜边BC上的高线AD折成一个二面角，此时∠BAC= 60 0，那么此二面角的大小为22、在正方体ABCD---A1B1C1D1中,∠A1B C1= ,与AC1成异面直线的棱有23、由0,1,2,3,4,5可以组成个无重复数字的三位数，可以组成个无重复数字的三为偶数。

考试时间：120分钟满分：100分一、选择题（每题5分，共30分）1. 下列各数中，无理数是（）。

A. √9B. √16C. √25D. √272. 已知a=2，b=-3，则a² - b²的值为（）。

A. -5B. 5C. -1D. 13. 如果一个等腰三角形的底边长为8cm，腰长为6cm，那么这个三角形的面积是（）。

A. 16cm²B. 24cm²C. 30cm²D. 32cm²4. 下列函数中，y是x的一次函数的是（）。

A. y = 2x + 3B. y = 3x² + 2C. y = 4x³ + 5D. y = 2x + 3x5. 在直角坐标系中，点A（-2，3）关于y轴的对称点B的坐标是（）。

A.（-2，-3）B.（2，-3）C.（2，3）D.（-2，3）二、填空题（每题5分，共20分）6. 已知sinθ = 0.5，那么cosθ的值是__________。

7. 二项式（a+b）⁵的展开式中，x³y²的系数是__________。

8. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数是__________。

9. 已知等差数列{an}的首项a₁=3，公差d=2，则第10项a₁₀=__________。

10. 圆的半径为r，则其周长的平方是__________。

三、解答题（每题20分，共60分）11. 解下列方程：（1）2x² - 5x + 3 = 0（2）3x - 2√x - 5 = 012. 已知函数f(x) = x² - 4x + 3，求f(x)在x=2时的函数值。

13. 在平面直角坐标系中，点P(2,3)和点Q(-3,2)关于原点对称的点分别是哪些？14. 已知等腰三角形ABC中，AB=AC，AD是BC边上的高，且AD=6cm，AB=8cm，求BC的长度。

中职学校高二上学期期中考《数学》试卷一、选择题（本大题共12小题，每题3分，共36分）1．下列事件中，属于必然事件的是（）A．明天会下雨B．掷一枚骰子点数为8C．某人的体温是36°D．今天星期四，明天星期五2．下列判断错误的是（）A．圆柱的侧面展开图是一个矩形.B．正三棱锥的三个侧面都是等腰三角形.C．三个平面最多可以把空间分隔成8块.D．过球面上任意两个不同点的大圆有且只有一个.3．若两条直线垂直于同一条直线，则这两条直线的位置关系是（）A．平行B．相交C．异面D．以上都有可能4．某校有1号2号3号三个大门，一次消防演习大门都开放，用于学生进出，则甲同学在演习过程中出去和返回，选择的大门可以有（）A．3种B.6种C．8种D．9种5．在空间四边形ABCD 中，已知点E、F、G、H 分别为边AB、BC、CD、DA 的中点，则直线EF、GH 的位置关系是（）A．异面B．相交C．平行D．以上都有可能6．若直线l 平行平面α内的直线b，则直线l 与平面α的位置关系A．平行B．直线l ⊂平面αC．//l α或l⊂αD．不确定7．有4套不同颜色的西装，另有5套不同样式的连衣裙，需选择其中一套服装参加元旦歌舞演出，则不同的选法种数共有（）种.A．4B．5C．9D．208．若圆锥的底面半径1r =，侧面积为4π，则圆锥的母线长为（）A．2B．3C．4D．5班级＿＿＿＿＿＿＿＿＿＿姓名＿＿＿＿＿＿＿＿＿＿学号＿＿＿＿＿＿＿＿＿试场号＿＿＿＿＿＿＿＿座位号＿＿＿＿＿＿＿＿装订线9．口袋内装有一些大小质地完全相同的红球2个、白球3个和黑球3个，从中摸出1个红球的概率是()A．13B．29C．0.25D．0.510．为进一步做好社区疫情防控工作，从医疗小组的2名医生和4名护士中各选派1人，去支援核酸检测，则不同的选派法共有（）种.A．2B．4C．6D．811.下列命题正确的是（）A．如果一条直线垂直于一个平面内无数条直线，则这条直线垂直于这个平面.B．若一条直线垂直于一个平面内的任意直线，则这条直线垂直于这个平面.C．过空间一点有且只有1条直线与已知直线垂直.D．垂直于同一个平面的两个平面一定垂直.12．如图正方体上的点P、Q、R、S是其所在棱的中点，则直线PQ与直线RS的夹角是（）A．30︒B．45︒C．60︒D．90︒二、填空题（本大题共7小题，每题3分，共21分）13．抛掷一枚骰子，“得到朝上面的点数为偶数”的概率为.14．如果圆柱的轴截面面积为4，高为2，则该圆柱底面圆的半径为.15.已知一个正三棱柱的底面边长为4cm,高为5cm,则这个正三棱柱的体积_________.16.现有4个班级秋游，要从3个景点中任选一个游览，则不同的选法共有种.17.球的大圆面积为π9，则该球的表面积为.18.边长为2的正方体的对角线长是.19.如图，正方体ABCD－A1B1C1D1中，E，F分别为AB，AD的中点，则B1C与EF所成角的大小为.（填度数）三、解答题（本大题共6小题，共43分）20.(本题共6分)设有5幅不同的国画，2幅不同的画，7幅不同的水彩画．(1)从中任选一幅画布置房间，有几种不同的选法(3分)；(2)从这些国画、油画、水彩画中各选一幅画布置房间，有几种不同的选法（3分）.21.（本题7分）．如图所示，一个圆柱形的玻璃杯的内半径为3cm，杯里所盛的水深度为5cm，现将一玻璃球浸入水中，水面高度上升到5.5cm，求玻璃球的体积及半径．22.(本题共7分)如图长方体A1B1C1D1−ABCD中，AB=4,1=3,BC=2,求：(1)异面直线1与DC所成角的大小(3分）；(2)D1B与平面ABCD所成的角的正切值（4分）.23.（本题共6分）用1，2，3，…，9共9个数字可组成多少个不同的(1)三位数(3分)；(2)无重复数字的三位数（3分）.24．（本题共7分）如图所示，已知三棱锥A-BCD 的侧棱AD 垂直于底面BCD，∆BCD 是边长为2的等边三角形，且AD=3，求二面角A-BC-D 的大小.25．（本题满分10分）如图所示，AD 为圆柱的母线，AC 为圆柱的下底面的直径，B 为下底面圆周上一点，若4AC AD ==，60BAC ∠=︒，（提示：直径所对的圆周角是直角！）求：（1）三棱锥D ABC -的体积（5分）；（2）二面角A BC D --的余弦值.（5分）．（第25题图）...............................................................................................................................................................................................................................................................装订线。

第1页中职二年级第一学期期中数学试卷考试时间：90分钟 满分：100分考查范围：集合 数列 三角函数一、选择题（每题4分，共48分）1．设A={1,2,3},B={2,3,4},则A ∪B=（ ）A ．{1,2,3,4}B ．{1,2,3}C ．{1,2,3,2,3,4}D ．{2,3}2.下列说法中正确的是（ ）A.第一象限的角一定是锐角B.锐角一定是第一象限的角C.小于90度的角一定是锐角D.第一象限的角一定是正角3．设数列为 ,11,22,5,2则24是该数列的 ( . )A.第9项B. 第10项C. 第11项D. 第12项4.等比数列{}n a 中, ,243,952==a a 则q 为（ ）A ． 3B ．4C ．5D ．65.以下四个数中,是数列{(1)}n n +中的一项的是( )A.380B.39C.32D.186. 1cos()4πα-=,则αcos 等于( ) A. 41- B. 41 C. 23 D. —23 7．数列根据项数的有限或无限可分为（ ）A ．有穷数列B ．无穷数列C ．有穷数列或无穷数列D ．以上都错8. 若ｘ∈[]π2,0，那么y =sin x 和 y =cos x 都是增函数的区间是（ ） A. )2,0(π B. ),2(ππ C. )23,(ππ D. )2,23(ππ 9. 0120cos =（ ） A. 21 B. —21 C. 23 D. —23 10.等比数列{}n a 中, ,243,952==a a 则{}n a 的前4项和为（ ）A ．81B ．120C ．168D ．19211．如果A 为锐角，1sin(),cos()2A A ππ+=--=那么（ ） A．2 B．2- C．2D．2- 12.点o o (sin600,cos300)在第几象限（ ）第2页A ．第一象限B ．第二象限C ．第三象限D ．第四象限二、填空（每题4分，共24分）13.设集合A={x|-1≤x ＜3},B={x|2<x ≤4}则A ∩B= ；14 .数列1.-2,3，-4,5的一个通项公式为 ；15.余弦函数y =cos x 的周期是___________；16.函数y =sinx +1的最大值是__________,最小值是_____________；17.等差数列—3，1，5，…的前15项的值是_____________；18. 等比数列1，23-，49，……的前5项和S 5= . 三、简答题：19.（6分）求cos(210)-的值。