分数乘法完整版

.分数乘整数〔一〕一、 心填写：1、 2 ＋ 2 ＋ 2=〔 〕×〔〕=〔〕1＋ 1＋ 1＋ 1=〔 〕×〔 〕=〔〕=〔〕7 7 76 6 6 62、5＋ 5 ＋ 5 ＋ 5 ＋⋯⋯＋ 5=〔 〕×〔〕 =〔〕=〔〕12 12 12 1212120个3、 2×4 表示〔〕。

54、8平方米 =〔〕平方分米3=〔 〕分2千米 =〔 〕米2545算式：5、〔〕与整数乘法的意 相同。

二、准确 算：2× 53 ×64 ×51319111×105× 85× 12612615 个 2 的和是多少？7的 9 倍是多少？518三、解决 ： 1、一个正方形5分米，它的周 多少分米？122、一种胡麻每千克 含油8千克， 1吨胡麻 含油多少千克？253、一批大米，每天吃去 1吨， 3天一共吃去多少吨？64、 一批大米，每天吃去1， 3天一共吃去几分之几？.2、分数乘整数〔二〕一、 心填写：1、3 ＋ 3＋ 3=〔 〕×〔 〕=〔〕3 ＋ 3 ＋ 3 ＋ 3=〔 〕×〔〕=〔〕=〔〕88 88 8 8 82、2 ＋ 2 ＋ 2 ＋ 2＋⋯⋯＋ 2=〔〕×〔〕=〔 〕=〔〕5 5 5 5 5100个3、 4 ×6 表示〔〕。

94、 2 米=〔〕厘米2=〔 〕分7千克 =〔〕克5310算式：二、准确 算：2×33×64× 97 5 213× 511×124×1510 162524 个 2是多少？5吨的 7 倍是多少吨？314三、解决 ：1、一个正三角形5米，它的周 多少米？62、一种 材每米重8千克， 在有 种 材500 米，共重多少千克？1253、小 和小明 自行 上学，小 每分 行4千米，小明每小 行15 千米。

他15的速度快？4、修一条公路，如果每天修 条路的2，8天能修完 ？.一个数乘分数〔一〕一、细心填写：1、 2×6 表示的意义是〔〕。

分数乘法分数乘整数完整版课件.一、教学内容本节课的教学内容选自人教版数学四年级上册第七单元第一课时，主要包括分数乘整数的计算法则及应用。

教材通过具体的生活情境和丰富的例题，引导学生理解分数乘整数的意义，掌握计算方法，并能灵活运用解决实际问题。

二、教学目标1. 理解分数乘整数的意义，掌握计算法则，能正确进行计算。

2. 培养学生的动手操作能力、观察分析能力、推理判断能力。

3. 培养学生运用数学知识解决实际问题的能力，提高学生学习数学的兴趣。

三、教学难点与重点重点：分数乘整数的计算法则及应用。

难点：理解分数乘整数的意义，掌握计算方法。

四、教具与学具准备教具：多媒体课件、黑板、粉笔。

学具：练习本、铅笔、橡皮。

五、教学过程1. 实践情景引入：展示一幅水果图片，图片中有2个苹果，每个苹果的面积是整个水果面积的1/4。

引导学生思考：如果要表示2个苹果的面积，应该怎样计算？2. 例题讲解：（1）展示例题：妈妈买了3个蛋糕，每个蛋糕切成了4块，一共吃了2块。

问：妈妈一共吃了几个蛋糕的块数？引导学生观察例题，发现妈妈吃的蛋糕块数是蛋糕总数（3个）乘以每块蛋糕的块数（4块），即3×4=12块。

然后，引导学生将蛋糕的块数用分数表示，即1个蛋糕=4块，妈妈吃了2块，所以妈妈吃了2/4个蛋糕。

引导学生用分数乘整数的方法计算妈妈吃的蛋糕块数，即3×(2/4)=6/4=1.5个蛋糕块。

3. 随堂练习：（1）完成练习册第1题：计算下列分数乘整数的结果。

a. 3/4 × 5b. 2/5 × 3（2）完成练习册第2题：应用分数乘整数的计算法则，解决实际问题。

a. 小明有2个苹果，每个苹果的重量是1/2千克，请问小明一共有多少千克的苹果？b. 小华买了5个面包，每个面包的长度是1/3米，请问小华一共买了多少米长的面包？4. 课堂讲解与练习：（1）讲解分数乘整数的计算法则，并通过多媒体展示分数乘整数的动画过程，让学生加深理解。

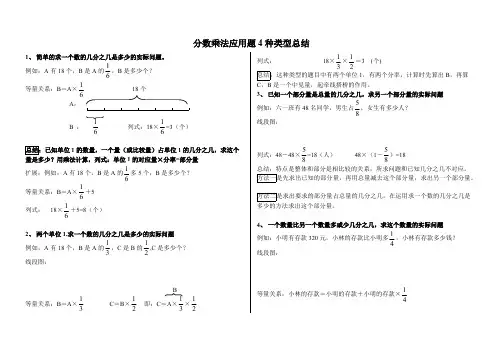
分数乘法应用题4种类型总结1、简单的求一个数的几分之几是多少的实际问题。

例如：A 有18个，B 是A 的，B 是多少个？61等量关系：B ＝A × 18个61A ：B ：列式：18×=3（个）6161总结：已知单位1的数量，一个量（或比较量）占单位1的几分之几，求这个量是多少？用乘法计算，列式：单位1的对应量×分率=部分量扩展：例如：A 有18个，B 是A 的多5个，B 是多少个？61等量关系：B ＝A ×＋561列式： 18×＋5=8（个） 612、两个单位1.求一个数的几分之几是多少的实际问题例如，A 有18个，B 是A 的，C 是B 的,C 是多少个？3121线段图： B 等量关系：B ＝A × C ＝B ×　即：C ＝A ××31213121列式： 18××＝3 (个) 3121总结：这种类型的题目中有两个单位1，有两个分率，计算时先算出B ，再算C ，B 是一个中见量，起牵线搭桥的作用。

3、已知一个部分量是总量的几分之几，求另一个部分量的实际问题例如：六一班有48名同学，男生占，女生有多少人？85线段图：列式：48－48×=18（人） 48×（1－）=188585总结：特点是整体和部分是相比较的关系，所求问题和已知几分之几不对应。

方法一是先求出已知的部分量，再用总量减去这个部分量，求出另一个部分量。

方法二是求出要求的部分量占总量的几分之几，在运用求一个数的几分之几是多少的方法求出这个部分量。

4、一个数量比另一个数量多或少几分之几，求这个数量的实际问题例如：小明有存款320元，小林的存款比小明多，小林有存款多少钱？41线段图：等量关系：小林的存款＝小明的存款＋小明的存款×41列式：320＋320×=400（元） 320×（1＋）=400（元）4141例如：小明有存款320元，小林的存款比小明多元，小林有存款多少钱？41线段图：等量关系：小林的存款＝小明的存款＋元41列式：320＋=（元） 4141320例如：六二班有男生25人，女生比男生少，女生有多少人？51线段图：等量关系：女生＝男生－男生×51列式：25－25×=20（人） 25×（1－）=20（人）5151总结：方法一：单位1的量±单位1的量×另一个数量比单位1多或少的几分之几=另一个数量方法二：单位1的量×（1±另一个数量比单位1多或少的几分之几）=另一个数量对应练习：(写出等量关系)1、一块长方形草坪，长30米，宽是长的。

个性化教学辅导教案
初夏早上六点，清亮透明的月儿还躲藏在云朵里，不忍离去，校园内行人稀少，我骑着单车，晃晃悠悠的耷拉着星松的睡眼。

校园内景色如常，照样是绿意盈盈，枝繁叶茂，鸟儿歌唱。

经过西区公园，看那碧绿的草地，飞翔中的亭子，便想起十七那年，在这里寻找春天的日子。

本想就此停车再感受一遍，可惜心中记挂北区的荷塘。

回想起冬日清理完荷塘的枯枝败叶，一片萧条的景色：湖水变成墨绿色，没有鱼儿游动，四处不见了鸟儿的踪影，只有莲藕躺在湖底沉沉睡去。

清洁大叔撑着竹竿，乘一叶扁舟，把一片片黑色腐烂的枯叶残枝挑上船。

几个小孩用长长的铁钩把莲蓬勾上岸，取下里头成熟的莲子。

六年级数学上册知识点整理归纳完整版六年级上册数学知识点第一单元分数乘法一）分数乘法意义1.分数乘整数的意义与整数乘法相同，即求几个相同加数的和的简便运算。

例如：3/4 × 7 表示求7个3/4的和是多少？2.一个数乘分数的意义是求一个数的几分之几是多少。

例如：5 × 2/3 表示求5的2/3是多少？二）分数乘法计算法则1.分数乘整数的运算法则是：分子与整数相乘，分母不变。

例如：2/3 × 4 = 8/32.分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

例如：2/3 × 1/2 = 2/6 = 1/3三）积与因数的关系一个数（除外）乘大于1的数，积大于这个数。

a ×b = c，当b。

1时，c。

a。

一个数（除外）乘小于1的数，积小于这个数。

a ×b = c，当b < 1时，c < a（b ≠ 0）。

一个数（除外）乘等于1的数，积等于这个数。

a ×b = c，当b = 1时，c = a。

四）分数乘法混合运算1.分数乘法混合运算顺序与整数相同，先乘、除后加、减，有括号的先算括号里面的，再算括号外面的。

整数乘法运算定律同样适用于分数乘法，运算定律可使计算更简便。

其中包括乘法交换律、乘法结合律和乘法分配律。

倒数的意义是指乘积为1的两个数互为倒数。

需要注意的是，倒数是两个数的关系，它们互相依存，不能单独存在。

判断两个数是否互为倒数的唯一标准是它们相乘的积是否为1.求倒数的方法包括求分数、整数、带分数和小数的倒数。

1的倒数是它本身，而0没有倒数，因为任何数乘以0的积都是0，且不能作分母。

任意数a（a≠0）的倒数为1/a，非零整数a的倒数为a/1，分数的倒数是倒数的分数。

真分数的倒数是假分数，真分数的倒数大于1，也大于它本身，而假分数的倒数小于或等于1，带分数的倒数小于1.分数乘法可用于解决各种问题。

例如，要求一个数的几分之几是多少，可以用单位“1”的量与分数相乘。

分数乘法分数乘整数完整版课件.一、教学内容本节课我们将学习《数学》教材第四章第三节的内容——分数乘法中的“分数乘整数”。

具体内容包括分数乘整数的概念、运算规则、应用举例以及相关性质。

二、教学目标1. 理解并掌握分数乘整数的运算规则，能够熟练地进行计算。

2. 能够将分数乘整数运用到实际问题中，提高解决问题的能力。

3. 通过学习分数乘整数，培养学生的逻辑思维能力和抽象概括能力。

三、教学难点与重点教学难点：分数乘整数运算规则的推导和应用。

教学重点：分数乘整数的运算方法及其在实际问题中的应用。

四、教具与学具准备1. 教具：PPT课件、黑板、粉笔。

2. 学具：练习本、铅笔、橡皮。

五、教学过程1. 实践情景引入通过一个实际问题引入分数乘整数：小明有一块巧克力，他吃掉了这块巧克力的1/4，那么如果他有4块同样的巧克力，他一共吃掉了多少？2. 探索新知引导学生通过小组合作，探讨分数乘整数的运算规则。

3. 例题讲解讲解分数乘整数的运算规则，通过例题演示计算过程。

例题1：计算1/4乘以4。

例题2：计算2/5乘以3。

4. 随堂练习练习1：计算3/7乘以5。

练习2：计算4/9乘以6。

5. 小结6. 应用拓展将分数乘整数运用到实际问题中，解决一些简单的实际问题。

六、板书设计1. 分数乘整数的概念2. 分数乘整数的运算规则3. 例题及解答4. 注意事项七、作业设计1. 作业题目：① 3/8乘以2② 5/6乘以4③ 7/9乘以3（2）应用题：小华有5块巧克力，他吃掉了每块巧克力的2/5，请问小华一共吃掉了多少巧克力？2. 答案：（1）① 3/4；② 10/3；③ 7/3（2）2块巧克力八、课后反思及拓展延伸1. 学生对分数乘整数运算规则的理解程度。

2. 学生在解决实际问题时，能否灵活运用所学知识。

3. 课后可布置一些拓展延伸题，提高学生的思维能力和应用能力。

例如：分数乘分数、整数乘分数等运算。

重点和难点解析1. 教学过程中的实践情景引入。

分数加减乘除口算题完整版分数加减乘除是数学中基本的运算符号，能够帮助我们在日常生活和学习中进行精确计算。

下面是一些关于分数加减乘除的口算题，希望能够帮助你巩固这些基本概念。

一、分数加法1. 1/8 + 3/8 = ?2. 5/6 + 2/6 = ?3. 2/3 + 1/5 = ?4. 9/10 + 1/2 = ?5. 3/4 + 2/5 = ?二、分数减法1. 3/4 - 1/4 = ?2. 2/3 - 1/3 = ?3. 5/6 - 1/6 = ?4. 7/8 - 3/8 = ?5. 9/10 - 2/5 = ?三、分数乘法1. 2/3 × 4/5 = ?2. 3/4 × 5/6 = ?3. 1/2 × 2/3 = ?4. 7/8 × 1/4 = ?5. 5/6 × 2/5 = ?四、分数除法1. 3/4 ÷ 2/3 = ?2. 4/5 ÷ 1/2 = ?3. 5/6 ÷ 3/4 = ?4. 2/3 ÷ 7/8 = ?5. 3/4 ÷ 1/5 = ?请你在纸上计算这些题目，然后在空格处填写正确答案。

答案：一、分数加法1. 1/8 + 3/8 = 4/8 = 1/22. 5/6 + 2/6 = 7/63. 2/3 + 1/5 = (2×5+1×3)/(3×5) = 13/154. 9/10 + 1/2 = (9×1+5×1)/(10×2) = 14/20 = 7/105. 3/4 + 2/5 = (3×5+2×4)/(4×5) = 23/20 = 1 3/20二、分数减法1. 3/4 - 1/4 = 2/4 = 1/22. 2/3 - 1/3 = 1/33. 5/6 - 1/6 = 4/6 = 2/34. 7/8 - 3/8 = 4/8 = 1/25. 9/10 - 2/5 = (9×5-2×2)/(10×5) = 41/50三、分数乘法1. 2/3 × 4/5 = (2×4)/(3×5) = 8/152. 3/4 × 5/6 = (3×5)/(4×6) = 15/24 = 5/83. 1/2 × 2/3 = 2/6 = 1/34. 7/8 × 1/4 = 7/325. 5/6 × 2/5 = 10/30 = 1/3四、分数除法1. 3/4 ÷ 2/3 = (3×3)/(4×2) = 9/8 = 1 1/82. 4/5 ÷ 1/2 = (4×2)/(5×1) = 8/5 = 1 3/53. 5/6 ÷ 3/4 = (5×4)/(6×3) = 20/18 = 10/94. 2/3 ÷ 7/8 = (2×8)/(3×7) = 16/215. 3/4 ÷ 1/5 = (3×5)/(4×1) = 15/4 = 3 3/4这些口算题能够帮助你熟悉和巩固分数的加减乘除运算。