向量的背景与共线概念.

平面向量的共线与共面平面向量是在平面上有大小和方向的矢量，可以用有向线段表示。

共线是指两个或多个向量具有相同的方向或相反的方向；共面是指多个向量所在的直线都在同一个平面上。

本文将从定义、判定条件、性质和几何意义等方面探讨平面向量的共线与共面。

一、定义平面向量是具有大小和方向的有序对。

用有向线段AB表示向量，表示为AB。

向量有起点A和终点B，起点和终点相同的向量为零向量，记作0。

在平面上，如果两个向量的起点或终点相同，则这两个向量是共线向量。

二、共线的判定条件两个向量共线的判定条件有两种：一种是通过向量的倍数关系判定，另一种是通过向量的坐标表示判定。

1. 倍数关系判定：给定两个向量a和b，如果存在一个数k，使得a=k·b，则a和b共线。

根据这一判定条件，可以得出两个向量共线的必要条件为它们的方向相同或相反。

2. 坐标表示判定：设向量a的坐标表示为a=(x1, y1)，向量b的坐标表示为b=(x2, y2)。

如果a、b不是零向量且有x1/x2=y1/y2，则a、b共线。

三、平面向量共线的性质共线向量具有以下性质：1. 共线向量的线性运算：对于共线向量a、b和任意实数k，有a+b和ka也是共线向量。

2. 共线向量的倍点共线：给定向量a和b，那么a和b的中点与a之间的向量、a和b的中点与b之间的向量也共线。

3. 共线向量的加法：对于共线向量a和b，它们之和等于共线化简为k个单位向量（k为实数），即a+b=k。

四、共面的判定条件三个平面向量A、B和C共面的判定条件为：存在实数x、y和z，使得A=x·B+y·C。

五、平面向量共面的性质共面向量具有以下性质：1. 共面向量的线性运算：对于共面向量A、B和任意实数x、y，有x·A+y·B也是共面向量。

2. 共面向量的线性组合：对于共面向量A1、A2、A3和任意实数x1、x2、x3，有x1·A1+x2·A2+x3·A3也是共面向量。

向量的共线公式向量的共线公式指的是两个向量在同一直线上的条件。

当两个向量在同一直线上时，它们被称为共线向量。

共线公式是判断两个向量是否共线的一种数学公式。

在本文中，将会介绍以下内容：什么是向量，向量的性质，向量的共线性，共线公式的推导方法和应用实例。

什么是向量？向量是数学中一个重要的概念，它是两个点之间的有向线段。

向量通常表示为箭头，箭头指向的方向表示向量的方向，箭头的长度表示向量的大小。

在直角坐标系中，一个向量可以由它的坐标表示。

向量的性质向量有以下的性质：1. 方向性：向量有明确的方向，可以用箭头来表示。

2. 数量性：向量有大小，可以用长度来表示。

3. 合成性：两个向量可以相加，合成成一个新向量。

合成向量的方向是两个原向量的方向之和，大小是两个原向量的长度之和。

4. 平移不变性：向量可以沿着直线平移而不改变它的性质。

5. 旋转不变性：向量可以绕着一个点旋转而不改变它的性质。

向量的共线性共线向量有以下的性质：1. 共线向量在同一直线上，方向相同或相反。

2. 共线向量的长度可以不同，但是它们的方向必须一致或相反。

3. 零向量与任何向量都是共线的。

4. 如果两个向量共线，那么其中一个向量可以表示为另一个向量的倍数。

也就是说，如果两个向量A和B共线，那么A=kB，其中k是一个实数。

共线公式的推导方法我们假设有两个向量A和B。

如果A和B共线，那么它们的方向相同或相反。

我们可以用向量的数量积(cosθ)来判断这两个向量的方向是否一致或相反。

向量的数量积定义为AB的模长|A|和B的模长|B|以及夹角θ的余弦值cosθ的乘积，即ABcosθ。

当A和B的方向一致时，θ=0度，如果两个向量A和B的数量积等于A的模长|A|乘以B的模长|B|，即ABcos0=|A||B|，那么这两个向量共线。

当A和B的方向相反时，θ=180度，如果两个向量A 和B的数量积等于-A的模长|A|乘以B的模长|B|，即ABcos180=-|A||B|，那么这两个向量共线。

6。

1 平面向量的概念本节课选自《普通高中课程标准数学教科书—必修第二册》（人教A 版）第六章《平面向量及其应用》,本节课是第1课时，本节课内容包括向量的实际背景与概念、向量的几何表示、相等向量与共线向量。

本节从物理学中的位移、力这些既有大小又有方向的量出发，抽象出向量的概念,并重点说明了向量与数量的区别，然后介绍了向量的几何表示、向量的长度、零向量、单位向量、平行向量、共线向量、相等向量等基本概念。

在“向量的物理背景与概念"中介绍向量的定义；在“向量的几何表示"中，主要介绍有向线段、有向线段的三个要素、向量的表示、向量与有向线段的区别与联系、向量的长度、零向量、单位向量、平行向量;在“相等向量与共线向量”中，主要介绍相等向量,共线向量定义等1。

教学重点：理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念，会表示向量.2.教学难点:平行向量、相等向量和共线向量的区别和联系.多媒体意的,单位向量的方向具体而定.（2）注意:向量是不能比较大小的，但向量的模（是正数或零）是可以进行大小比较的。

例1。

在图中，分别用向量表示A地至B、C两地的位移，并根据图中的比例尺，并求出A地至B、C两地的实际距离(精确到1km）（三）。

相等向量与共线向量思考1:向量由其模和方向所确定.对于两个向量b a,，就其模等与不等，方向同与不同而言，有哪几种可能情形？【答案】模相等，方向相同；模相等，方向不相同;模不相等，方向相同; 模不相等,方向不相同；1.平行向量定义：[来源：学科网ZXXK]通过例题进一步理解向量的概念，提高学生用向量解决问题的能力。

通过思考，引入平行向量，提高学生的理解问题的能力。

①方向相同或相反的非零向量叫平行向量；②我们规定0与任一向量平行。

说明：（1）综合①、②才是平行向量的完整定义；(2)向量ａ、ｂ、ｃ平行,记作ａ∥ｂ∥ｃ.2。

相等向量定义：长度相等且方向相同的向量叫相等向量.说明:（1)向量ａ与ｂ相等，记作ａ＝ｂ；（2）零向量与零向量相等;（3）任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线．．．．段的起点无关．．．．．．。

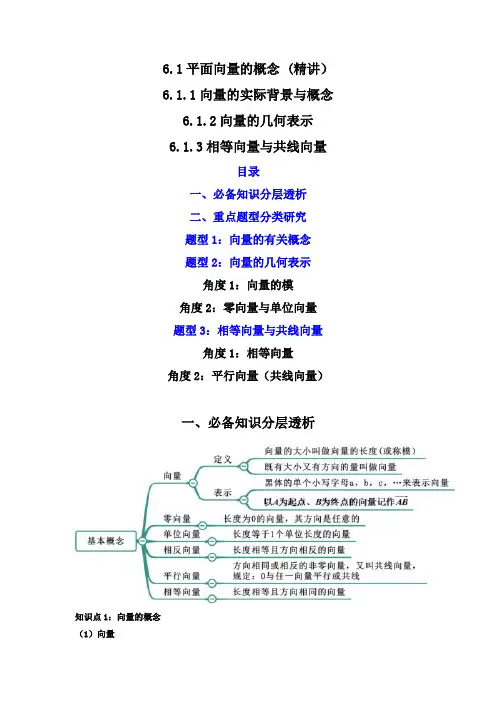
6.1平面向量的概念 (精讲）6.1.1向量的实际背景与概念6.1.2向量的几何表示6.1.3相等向量与共线向量目录一、必备知识分层透析二、重点题型分类研究题型1：向量的有关概念题型2：向量的几何表示角度1：向量的模角度2：零向量与单位向量题型3：相等向量与共线向量角度1：相等向量角度2：平行向量（共线向量）一、必备知识分层透析知识点1：向量的概念（1）向量在数学中,我们把既有大小又有方向的量叫做向量.①我们所学的向量是自由向量,即只有大小和方向,而无特定的位置,这样的向量可以作任意平移.②向量与向量之间不能比较大小.（2）数量只有大小没有方向的量称为数量,如年龄、身高、长度、面积体积、质量等（3）向量与数量的区别①向量与数量的区别:向量有方向,而数量没有方向；数量与数量之间可以比较大小,而向量与向量之间不能比较大小②向量与矢量:数学中的向量是从物理中的矢量(如位移、力、加速度、速度等)中抽象出来的,但在这里我们仅考虑它的大小及方向；而物理中的这些量,既同时具备大小和方向这两个属性,还具有其他属性(如“力”就是由大小方向、作用点所决定的).知识点2：向量的几何表示(1)有向线段具有方向的线段叫做有向线段①有向线段:具有方向的线段叫做有向线段,其方向是由起点指向终点.以A为起点、B为终AB. 表点的有向线段记作AB(如图所示),线段AB的长度也叫做有向线段的长度,记作||示有向线段时,起点一定要写在终点的前面,上面标上箭头.②有向线段的三个要素:起点、方向、长度.知道了有向线段的起点、方向、长度,它的终点就唯一确定了.（2）向量的表示①几何表示:向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向.②字母表示:向量可以用字母a,b,c,…表示（3）向量的模AB.向量AB的大小称为向量AB的长度(或称模),记作||（4）两种特殊的向量零向量:长度为0的向量叫做零向量,记作0.单位向量:长度等于1个单位长度的向量,叫做单位向量①若用有向线段表示零向量,则其终点与起点重合.与0的区别与联系,0是一个向量|0|；书写时0表示零向量方向相同或相反的非零向量叫做平行向量.向量a 与b 平行,记作a b .规定:零向量与任意即对于任意向量a ,都有0a .长度相等且方向相同的向量叫做相等向量.向量a 与b 相等,记作a b =.两个向量相等必须具备的条件是长度相等,方向相同因为向量完全由它的方向和模确定,故任意两个相等的非零向量与有向线段的起点无关.）共线向量任一组平行向量都可以平移到同一条直线上共线向量所在直线平行或重合,如果两个向量所在的直线平行或重合·高一课时练习）下列四个命题正确的是（ ）．若a 与b 不共线，则a 与b 都是非零向量．两个相等的向量起点、方向、长度必须都．（2022·全国·高一专题练习）下列命题中，正确的是||||a b =，则a b =．若a b =，则||||a b = ||||a b >，则a b > ||0a =，则0a = ．（2022·全国·高一假期作业）有下列命题：①两个相等向量，若它们的起点相同，则终点也相同；②若||a b |=|，则a b =； ③若AB DC =，则四边形ABCD 是平行四边形；m n =，n k =，则m k =；⑤若//a b ，//b c ，则//a c ； ⑥有向线段就是向．（2022·高一课时练习）下列说法正确的是（．向量AB与向量BA的长度相等例题2．（BD=________.例题3．（·全国·高一专题练习）若在一个边长为的正三角形所对应的有向线段为AD（其中则向量AD的模的最小值为高一专题练习）如果一架飞机向东飞行200 km，再向南飞行机飞行的路程为s，位移为a，那么（a aa a不能比大小2022·高一课时练习）已知在边长为ABCD中，∠，则BD=2022·高一课时练习）已知圆O的周长是，AB是圆O的直径，是圆周上一点，π=⊥CD=___________.,CD角度2：零向量与单位向量典型例题．向量就是有向线段>，则a b||||a b>．（2022秋·新疆巴音郭楞·高一校考阶段练习）下列说法正确的是（e=．单位向量均相等．单位向量1．零向量与任意向量平行．若向量a，b满足||||a b=，则a b=±．（2022秋·广东东莞·高一校联考期中）下列说法错误的是（．若0a =，则0a =．零向量是没有方向的 ．（多选）（2022春·广东佛山向量的说法正确的是（ ）．单位向量：模为1的向量例题1．（2022春·广东揭阳·中，AB DC =，则下列向量相等的是（．AD 与CB．OC 与OA ．AC 与DB D ．DO OB =例题2．（2022·全国·高三专题练习）“a b =”是“||||a b =”的（ ．充分非必要条件B ．必要非充分条件 ．充分必要条件 D ．既非充分又非必要条件例题3．（多选）（2022·高一课时练习）下列说法中错误的是（ ）||||a b =，则a b = B ．若a b ≠，则||||a b ≠||||a b =，则a 与b 可能共线||||a b ≠，则a 一定不与b 共线(1)分别写出与AO 、BO 相等的向量；写出与AO 共线的向量；写出与AO 的模相等的向量；写出与AO 的夹角为90︒的向量；向量AO 与CO 是否相等？（多选）（2022秋·浙江嘉兴若非零向量a ，b ，下列命题正确的是．若a b =，则a b =．若a b =，则a b = ．若//a b ，则a b = ．若a b =，则//a b．（多选）（2022秋·山东菏泽高一统考期中）设点O 是平行四边形ABCD 点，则下列结论正确的是（ ）．AO OC = B ．AO BO = ．AO BO = D ．AB 与CD 共线 ．（2022·高一课时练习）如图所示，在平行四边形ABCD 中，E ，F 分别是CD ，AB 中点.(1)写出与向量FC 共线的向量；(2)求证：BE FD =.4．（2022·全国·高三专题练习）在平行四边形ABCD 中，E ，F 分别为边AD 、BC 的中点，如图．(1)写出与向量FC 共线的向量；(2)求证：BE FD =．角度2：平行向量（共线向量）典型例题例题1．（2022春·河南·高三校联考阶段练习）已知,,,A B C D 为平面上四点，则“向量AB CD ∥”是“直线AB CD ”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件例题2．（2022秋·上海杨浦·高一复旦附中校考期中）①加速度是向量；②若//a b 且//b c ，则//a c ；③若AB CD =，则直线AB 与直线CD 平行．上面说法中正确的有（ ）个．A ．0B ．1C ．2D ．3同类题型演练1．（2022秋·湖北·高一校联考期中）“//b a ”是“a b =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．（2022秋·上海浦东新·高一校考期末）命题：若//,//a b b c ，则//a c ，则命题为_______（填写：真命题或假命题）3．（2022·高一课时练习）已知命题“若//a b ，//b c ，则//a c ”是假命题，则b =__________.。

简析高校经济责任审计风险的成因及防控对策2022年7月，国家在综合实践经验的基础上，为适应十八大以来形势发展的需要，中央纪委机关牵头七部门联合发布《党政主要领导干部和国有企业领导人员经济责任审计规定实施细则》，此举表明我国经济责任审计工作推进到了新的阶段。

新发布的细则明确并完善了经济责任审计的对象、内容、评价、报告、结果运用和组织领导与实施等内容。

这为高校经济责任审计工作指明了方向，也对高校有关领导者和审计人员提高审计质量、防控审计风险提出了新的要求。

一、高校经济责任审计风险的特点高校经济责任审计风险，是指高校审计人员在实施审计行为的过程中，基于各类因素影响而漏判或者误判了责任人应负的责任，发表了与真实状况不一致的审计评价，致使被审计方产生损失，并引起审计部门及人员承担相应责任的可能性。

该风险具有如下几个特点:一是客观性。

在政策变化、业务复杂、相关责任人道德水平等因素的影响下，容易产生审计结果与事实不相符的状况。

虽然有的风险没有造成十分严重的后果，或者审计人员尚未发生实际的损失，但是风险总是存在于审计活动之中。

因此，相关人员易于了解并防控审计风险，也往往能于时空制约下控制风险滋生及发展的条件，但对彻底消除风险却无能为力。

二是不确定性。

审计风险来自于客观因素抑或审计人员的主观认识。

风险发生的环节、所属的性质、产生的后果和影响在审计之前较难判断。

同时，由于高校经济责任范围的广泛性，当前的审计方法无法实现全方位覆盖，这也加大了风险的偶然性与不确定性。

三是敏感性。

若经济责任审计评价无法真实反映客观实际，不但会对经济责任人所在部门或单位的决策造成影响，也会限制责任人的任用，甚至导致湮灭审计信誉，降低群众信任度。

因而，该类误判所导致的后果比其他类型审计更严重，人们所能接受的误差也小得多，审计风险更高。

四是可控性。

审计风险的客观性增加了经济责任审计的难度，但是经过经验积累与主观努力，随着法规、制度的完善，利用改进的审计手段，能够实现把审计风险控制在合理范围内，最大限度减少失误。

向量的三点共线定理一、概念向量的三点共线定理，又称之为向量的共线定理，是向量理论中的一个基本定理。

它描述了在三维空间中，如果三个点A、B、C由向量OA、OB、OC表示，并且存在实数λ和μ，使得OC = λOA + μOB，且λ+ μ= 1，则这三个点A、B、C是共线的。

二、定义定义1：共线向量，也称为平行向量，是指方向相同或相反的非零向量。

在平面或空间中，如果两个向量有相同的方向或相反的方向，则这两个向量被称为共线向量。

定义2：如果三个点A、B、C满足OC = λOA + μOB，其中λ和μ是实数，并且λ+ μ= 1，则称这三个点A、B、C是共线的。

三、性质性质1：若三点A、B、C共线，则它们的位置向量之间存在线性关系，即OC = λOA + μOB，且λ+ μ= 1。

性质2：若向量a与向量b共线，则存在唯一实数k，使得a = kb。

特别地，当k = 1时，a与b方向相同；当k = -1时，a与b方向相反。

性质3：共线向量的模长之比等于它们对应分量之比，即若a = kb，则|a|/|b| = |k|。

四、特点特点1：向量的三点共线定理是向量线性组合的一个特殊情况，它揭示了向量之间的线性关系与点的几何位置之间的关系。

特点2：该定理提供了一种通过向量运算判断三点是否共线的方法，为向量在空间中的应用提供了便利。

特点3：向量的三点共线定理与平面几何中的三点共线定理具有类似的性质，但向量的表达方式更具一般性，可以推广到三维空间乃至更高维的向量空间。

五、规律规律1：如果三点A、B、C共线，那么它们的位置向量OA、OB、OC之间存在唯一的线性关系，使得OC = λOA + μOB，且λ+ μ= 1。

这个线性关系中的λ和μ是唯一的，除非A、B、C三点重合。

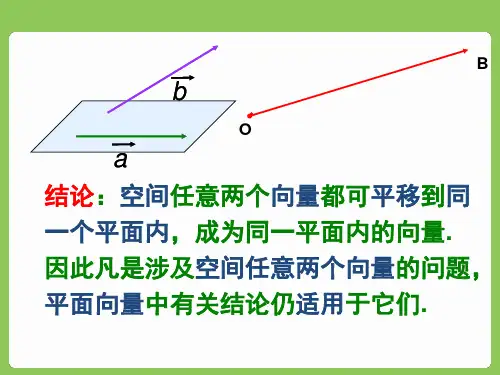
规律2：在三维空间中，如果三个向量a、b、c满足a = λb + μc，且λ+ μ= 1，则这三个向量是共面的。

特别地，当这三个向量是三个点的位置向量时，这三个点共线。

共面、共线、平行向量的定义及判定向量是数学中一个极为重要的概念，它的应用范围广泛，不仅存在于高等数学、线性代数中，也广泛应用于物理、力学等学科。

作为向量中的重点概念，共面、共线、平行向量在向量的运算及应用中有着不可忽略的地位。

本文将详细介绍这三种向量的定义及判定方法。

共面向量共面向量指的是三维向量中处于同一个平面内的向量。

形式上，如果有3个向量a、b、c，且它们处于同一平面内，则称它们是共面向量。

我们可以通过向量的线性组合来判断向量是否共面。

具体来说，设有三个向量a1、a2、a3①当a1、a2、a3线性无关时，它们不共面。

②当a1、a2、a3线性相关时，可通过向量线性组合来判断它们是否共面。

如果能够用a1、a2、a3的线性组合表示出零向量，则a1、a2、a3共面。

如果不能表示为零向量，则a1、a2、a3不共面。

共线向量共线向量指的是两个或多个向量在同一条直线上的向量。

若有2个向量a、b，则称它们是共线向量。

与共面向量类似，我们也可以通过向量的线性组合来判断向量是否共线。

具体来说，设有两个向量a、b①当向量a、b不共线时，它们不共线。

②当向量a、b共线时，可通过向量线性组合来判断它们是否共线。

如果我们可以用一个实数k表示向量a、b，即满足b=ka，则a、b共线。

否则，a、b不共线。

平行向量平行向量指的是在同一平面内且方向相同或相反的向量。

若有两个向量a、b，则称它们是平行向量。

平行向量的判定方法有两种：一是通过向量积判定，二是直接比较方向。

①通过向量积判断：当向量a、b的向量积（即叉积）等于0时，它们是平行向量。

即axb=0。

②通过比较方向判断：当向量a、b的方向相同或相反时，它们是平行向量。

具体来说，可以通过判断两个向量内每个坐标上的值的比例是否相等来确定向量的方向是否相同。

总之，对于向量的共面、共线、平行关系，我们需要通过向量线性组合、向量积判定、直接比较向量方向等方法来进行判断。

熟练掌握判断方法，可以使我们更好地理解向量的性质及操作规律。