计量经济学课后习题答案第八章_答案

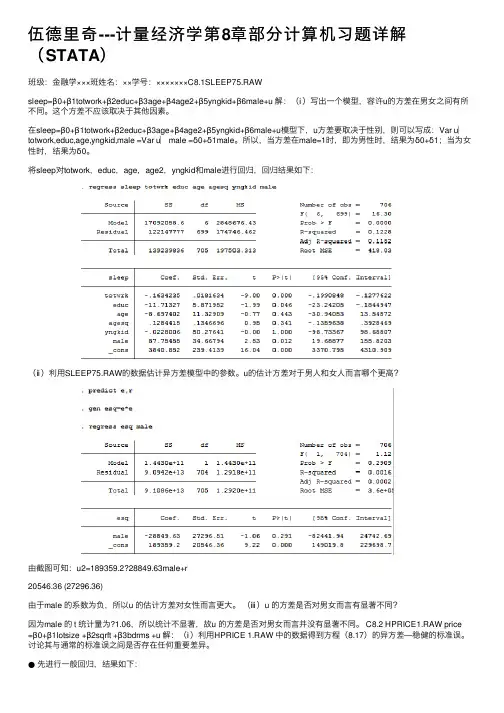
伍德⾥奇---计量经济学第8章部分计算机习题详解（STATA）班级：⾦融学×××班姓名：××学号：×××××××C8.1SLEEP75.RAWsleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u 解：（ⅰ）写出⼀个模型，容许u的⽅差在男⼥之间有所不同。

这个⽅差不应该取决于其他因素。

在sleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u模型下，u⽅差要取决于性别，则可以写成：Var u︳totwork,educ,age,yngkid,male =Var u︳male =δ0+δ1male。

所以，当⽅差在male=1时，即为男性时，结果为δ0+δ1；当为⼥性时，结果为δ0。

将sleep对totwork，educ，age，age2，yngkid和male进⾏回归，回归结果如下：（ⅱ）利⽤SLEEP75.RAW的数据估计异⽅差模型中的参数。

u的估计⽅差对于男⼈和⼥⼈⽽⾔哪个更⾼？由截图可知：u2=189359.2?28849.63male+r20546.36 (27296.36)由于male 的系数为负，所以u 的估计⽅差对⼥性⽽⾔更⼤。

（ⅲ）u 的⽅差是否对男⼥⽽⾔有显著不同？因为male 的 t 统计量为?1.06，所以统计不显著，故u 的⽅差是否对男⼥⽽⾔并没有显著不同。

C8.2 HPRICE1.RAW price =β0+β1lotsize +β2sqrft +β3bdrms +u 解：（ⅰ）利⽤HPRICE 1.RAW 中的数据得到⽅程（8.17）的异⽅差—稳健的标准误。

讨论其与通常的标准误之间是否存在任何重要差异。

●先进⾏⼀般回归，结果如下：●再进⾏稳健回归，结果如下：由两个截图可得：price =?21.77+0.00207lotsize +0.123sqrft +13.85bdrms29.48 0.00064 0.013 (9.01)37.13 0.00122 0.018 [8.48]n =88，R 2=0.672⽐较稳健标准误和通常标准误，发现lotsize 的稳健标准误是通常下的2倍，使得 t 统计量相差较⼤。

实验一P42第二章第6题=+GDP+Dependent Variable: YMethod: Least SquaresDate: 01/11/08 Time: 09:03Sample: 1985 1998Included observations: 14Variable Coefficient Std.Errort-Statistic Prob.C12596.271244.56710.121010.0000GDP26.954154.1203006.5417920.0000 R-squared0.781002 Meandependent var20168.57Adjusted R-squared 0.762752 S.D. dependentvar3512.487S.E. of regression 1710.865 Akaike infocriterion17.85895Sum squared resid 35124719 Schwarzcriterion17.95024Log likelihood-123.0126 F-statistic42.79505Durbin-Watsonstat0.859998 Prob(F-statistic)0.000028(10.1) ( 6.5), =0.78 =0.76（一）对回归方程的结构分析：是这个样本回归方程的斜率，它表示GDP每增加1亿元，某市将增加26.95的货物运输量；是样本回归方程的截距，它表示不受GDP影响的某市的货物运输量。

（二）统计检验=0.78，说明总离差平方和的78%被样本回归直线解释，有22%未被解释，因此，样本回归直线的拟合优度是可以的。

给出显著水平，查自由度v=14-2=12的t分布表，得临界值，，，固回归系数均显著不为零，回归模型中应包含常数项，GDP对Y有显著影响。

（三）预测2000年的某市货物运输量假如2000年某市以1980年不变价的国内生产总值为620亿元，得到2000年货物运输量的预测值29307.84万吨。

第八章虚拟变量模型1. 回归模型中引入虚拟变量的作用是什么?答:在模型中引入虚拟变量，主要是为了寻找某(些)定性因素对解释变量的影响。

加法方式与乘法方式是最主要的引入方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

2. 虚拟变量有哪几种基本的引入方式? 它们各适用于什么情况?答:在模型中引入虚拟变量的主要方式有加法方式与乘法方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

3．什么是虚拟变量陷阱？答：根据虚拟变量的设置原则，一般情况下，如果定性变量有m个类别，则需在模型中引入m-1个变量。

如果引入了m个变量，就会导致模型解释变量出现完全的共线性问题，从而导致模型无法估计。

这种由于引入虚拟变量个数与类别个数相等导致的模型无法估计的问题，称为“虚拟变量陷阱”。

4．在一项对北京某大学学生月消费支出的研究中，认为学生的消费支出除受其家庭的每月收入水平外，还受在学校中是否得到奖学金，来自农村还是城市，是经济发达地区还是欠发达地区，以及性别等因素的影响。

试设定适当的模型，并导出如下情形下学生消费支出的平均水平：(1) 来自欠发达农村地区的女生，未得到奖学金；(2) 来自欠发达城市地区的男生，得到奖学金；(3) 来自发达地区的农村女生，得到奖学金；(4) 来自发达地区的城市男生，未得到奖学金。

解答: 记学生月消费支出为Y，其家庭月收入水平为X，则在不考虑其他因素的影响时，有如下基本回归模型：Y i=β0+β1X i+μi有奖学金1 来自城市无奖学金0 来自农村来自发达地区 1 男性0 来自欠发达地区0 女性Y i=β0+β1X i+α1D1i+α2D2i+α3D3i+α4D4i+μi由此回归模型，可得如下各种情形下学生的平均消费支出：(1) 来自欠发达农村地区的女生，未得到奖学金时的月消费支出：E(Y i|= X i, D1i=D2i=D3i=D4i=0)=β0+β1X i(2) 来自欠发达城市地区的男生，得到奖学金时的月消费支出：E(Y i|= X i, D1i=D4i=1,D2i=D3i=0)=(β0+α1+α4)+β1X i(3) 来自发达地区的农村女生，得到奖学金时的月消费支出：E(Y i |= X i , D 1i =D 3i =1,D 2i =D 4i =0)=(β0+α1+α3)+β1X i (4) 来自发达地区的城市男生，未得到奖学金时的月消费支出： E(Y i |= X i ,D 2i =D 3i =D 4i =1, D 1i =0)= (β0+α2+α3+α4)+β1X i5. 研究进口消费品的数量Y 与国民收入X 的模型关系时，由数据散点图显示1979年前后Y 对X 的回归关系明显不同，进口消费函数发生了结构性变化：基本消费部分下降了，而边际消费倾向变大了。

第八章练习题及参考解答8.1 Sen 和Srivastava （1971）在研究贫富国之间期望寿命的差异时，利用101个国家的数据，建立了如下的回归模型：2.409.39ln3.36((ln 7))i i i i Y X D X =-+--(4.37) (0.857) (2.42) R 2=0.752其中：X 是以美元计的人均收入；Y 是以年计的期望寿命；Sen 和Srivastava 认为人均收入的临界值为1097美元（ln10977=），若人均收入超过1097美元，则被认定为富国；若人均收入低于1097美元，被认定为贫穷国。

括号内的数值为对应参数估计值的t-值。

1）解释这些计算结果。

2）回归方程中引入()ln 7i i D X -的原因是什么？如何解释这个回归解释变量？ 3）如何对贫穷国进行回归？又如何对富国进行回归？ 4）从这个回归结果中可得到的一般结论是什么？ 练习题8.1参考解答： 1. 结果解释依据给定的估计检验结果数据，对数人均收入对期望寿命在统计上并没有显著影响，截距和变量()ln 7i i D X -在统计上对期望寿命有显著影响；同时，()()2.40 3.3679.39 3.36ln ((ln 7)) 1 2.409.39ln 0 i i i i i i i X D X D Y X D ⎧-+⨯+---==⎨-+=⎩富国时穷国时 表明贫富国之间的期望寿命存在差异。

2. 回归方程中引入()ln 7i i D X -的原因是从截距和斜率两个方面考证收入因素对期望寿命的影响。

这个回归解释变量可解释为对期望寿命的影响存在截距差异和斜率差异的共同因素。

3. 对穷国进行回归时，回归模型为12ln 1097i i i i i i Y X Y X αα=+≤，其中，为美元时的寿命； 对富国进行回归时，回归模型为12ln 1097i i i i i i Y X Y X ββ=+>，其中，为美元时的寿命；4. 一般的结论为富国的期望寿命药高于穷国的期望寿命，并且随着收入的增加，在平均意义上，富国的期望寿命的增加变化趋势优于穷国，贫富国之间的期望寿命的确存在显著差异。

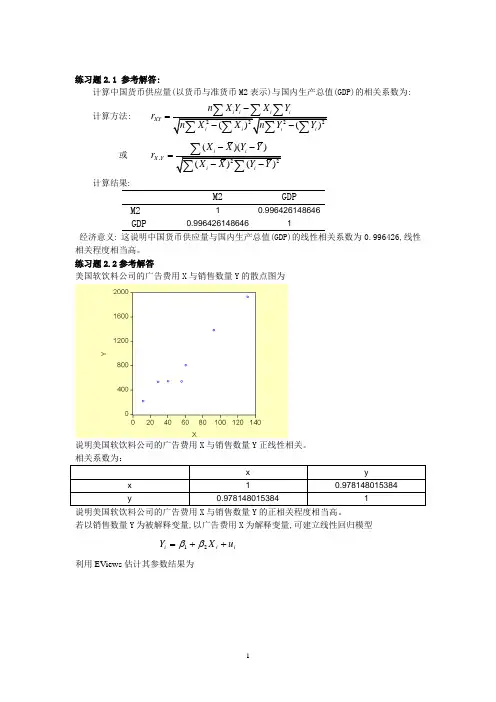
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或,()()X Y X X Y Y r --=计算结果:M2GDPM2 10.996426148646GDP0.9964261486461经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。

练习题2.2参考解答美国软饮料公司的广告费用X 与销售数量Y 的散点图为说明美国软饮料公司的广告费用X 与销售数量Y 正线性相关。

相关系数为：说明美国软饮料公司的广告费用X 与销售数量Y 的正相关程度相当高。

若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。

回归结果表明，广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。

练习题2.3参考解答: 1、 建立深圳地方预算内财政收入对GDP 的回归模型，建立EViews 文件，利用地方预算内财政收入（Y ）和GDP 的数据表，作散点图可看出地方预算内财政收入（Y ）和GDP 的关系近似直线关系，可建立线性回归模型： t t t u GDP Y ++=21ββ 利用EViews 估计其参数结果为即 ˆ20.46110.0850t tY GDP =+ （9.8674） (0.0033)t=(2.0736) (26.1038) R 2=0.9771 F=681.4064经检验说明,深圳市的GDP 对地方财政收入确有显著影响。

20.9771R =，说明GDP 解释了地方财政收入变动的近98%，模型拟合程度较好。

模型说明当GDP 每增长1亿元时，平均说来地方财政收入将增长0.0850亿元。

第八章一、名词解释1、虚拟变量：在建立模型时，有一些影响经济变量的因素无法定量描述，如职业、性别对收入的影响，教育程度，季节因素等往往需要用定性变量度量。

为了在模型中反映这类因素的影响，并提高模型的精度，需要将这类变量“量化”。

根据这类边另的属性类型，构造仅取“0”或“1”的人工变量，通常称这类变量为“虚拟变量”2、虚拟变量陷阱：一般在引入虚拟变量时要求如果有m个定性变量，字在模型中引入m-1个虚拟变量。

否则，如果引入m个虚拟变量，就会导致模型解释变量间出现完全共线性的情况。

我们一般称由于引入虚拟变量个数与定性因素个数相同出现的模型无法估计的问题，称为“虚拟变量陷阱”二、单项选择题1、B：“地区”一个，“季节”三个2、A：将D=1代入估计后的方程即可3、D：“季节”包含4个类型，只能用3个虚拟变量，用4个虚拟变量会出现完全多重共线的问题，参数将无法估计4、C：“地区”只有两个类别，引入两个虚拟变量会出现完全多重共线问题5、A：1α体现了城镇和农村截距上的差异，1β体现了城镇和农村斜率上的差异，当它们为0时，表示无差异6、A：斜率相同，仅截距不同7、D：此问题表现为1000前后斜率的变化，B表示截距的变化，不合适；C在D=0时没有解释变量，不正确；A和D相比，D更合适，A会造成曲线在临界值出断开，但D会保证曲线的连贯的。

8、A：虚拟变量表示性别、季节等时，只表示属性的不同，没有等级之分，作为质的因素；表示收入高低时，高与低是有级别的，属于有序数据，可以表示数量的因素。

9、A/B：这题比较牵强，按书上原话应该选择B；但当用加法引入虚拟变量时，会存在问题。

【当用加法形式引入虚拟变量时，用一个虚拟变量作为截距项，取值全部为1；其他m-1个表示该因素的前三个类型。

如果不引入截距项，当虚拟变量都取0时不能解释该因素第四个类型的作用。

】10、D ：概念性三、多项选择题1、B C D ：A 太绝对，也可以表示数量因素；E 太绝对2、ABCDE ：A 加法方式；B 乘法方式；C 临界指标的虚拟变量；D 在ABC 基础上可构造分段回归3、AB ：C 当虚拟变量取0或2时，过程一样，但参数的意义稍作调整；D 见书P207倒数第二段。

计量经济学（第四版）习题参考答案潘省初第一章 绪论1.1 一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说） （2）建立计量经济模型 （3）收集数据 （4）估计参数 （5）假设检验 （6）预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量，但它（它们）仅是影响因变量的主要因素，还有很多对因变量有影响的因素，它们相对而言不那么重要，因而未被包括在模型中。

为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。

1.3时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。

横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。

如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。

1.4 估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。

在一项应用中，依据估计量算出的一个具体的数值，称为估计值。

如Y 就是一个估计量，1nii YY n==∑。

现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。

第二章 计量经济分析的统计学基础2.1 略，参考教材。

2.2 NSS x ==45=1.25用=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。

2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/2510/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。

计量经济学第二版第八章答案【篇一：庞皓计量经济学课后答案第八章】业1、①在给定的数据中可以看出人均收入的系数的t值t(?2)?0.857，di(lnxi?7)系数的t值t(?3)?2.42，在给定显著性水平??0.05下n=101，t0.025(101)?1.984。

所以人均收入对期望寿命并没有显著影响。

而di(lnxi?7)对期望寿命有显著影响。

当人均收入超过1097美元时，即di=1为富国时：???2.40?9.39lnx?3.36(lnx?7)?21.12?6.03lnx yiiii当人均收入未超过1097美元时，即di=0为穷国时：???2.40?9.39lnx yii②引入di(lnxi?7)的原因是从截距和斜率两个方面来考虑收入对期望寿命的影响。

③对穷国进行回归时，yi取xi?1097时的值。

对富国进行回归时，yi取xi?1097时的值④结论：富国的期望寿命高于穷国的期望寿命。

贫富国之间的期望寿命的确存在显著差异。

2、①d1t???1,t为1987年及以后?0,t为1987年以前 d2t??年及以后?1,t为1994年以前?0,t为1994年及以后年及以后?1,t为2006?1,t为2008 d3t?? d4t?? 0,t为2006年以前0,t为2008年以前??②从图形上看。

consume和income 及employment存在线性相关关系。

而与burden从图形上看不出线性关系。

所以对模型的设定保持怀疑态度。

③?umecons.16?0.63incomeconsume.51employmentt?1674t?0.0 86t?1?537t?202.50burden.27d2t?127.04d3t?172.2d4tt?7.22d1t?194r2?0.9998672?0.99979 2 f=13189.98 dw=2.921拟合效果好，且通过dw检验由回归可知consumet，d1td3t的系数未能通过显著性水平??0.05下的tt?1，burden检验。

计量经济学各章习题第一章绪论1.1试列出计量经济分析地主要步骤.1.2计量经济模型中为何要包括扰动项?1.3什么是时间序列和横截面数据? 试举例说明二者地区别1.4估计量和估计值有何区别？第二章计量经济分析地统计学基础2.1名词解释随机变量概率密度函数抽样分布样本均值样本方差协方差相关系数标准差标准误差显著性水平置信区间无偏性有效性一致估计量接受域拒绝域第I 类错误2.2请用例 2.2中地数据求北京男生平均身高地99％置信区间.2.325 个雇员地随机样本地平均周薪为130元，试问此样本是否取自一个均值为120 元、标准差为10 元地正态总体？文档收集自网络，仅用于个人学习2.4某月对零售商店地调查结果表明，市郊食品店地月平均销售额为2500 元，在下一个月份中，取出16 个这种食品店地一个样本，其月平均销售额为2600 元，销售额地标准差为480 元.试问能否得出结论，从上次调查以来，平均月销售额已经发生了变化？文档收集自网络，仅用于个人学习第三章双变量线性回归模型3.1判断题（判断对错；如果错误，说明理由）（1）OLS 法是使残差平方和最小化地估计方法.（2）计算OLS 估计值无需古典线性回归模型地基本假定.（3）若线性回归模型满足假设条件（1）～（4），但扰动项不服从正态分布，则尽管OLS 估计量不再是BLUE ，但仍为无偏估计量.文档收集自网络，仅用于个人学习（4）最小二乘斜率系数地假设检验所依据地是t 分布，要求地抽样分布是正态分布.2（5）R2＝TSS/ESS.（6）若回归模型中无截距项，则.（7）若原假设未被拒绝，则它为真.（8）在双变量回归中，地值越大，斜率系数地方差越大.3.2设和分别表示Y 对X 和X 对Y 地OLS 回归中地斜率，证明r 为X 和Y 地相关系数.3.3证明：（1）Y 地真实值与OLS 拟合值有共同地均值，即；（2）OLS 残差与拟合值不相关，即.3.4证明本章中（ 3.18）和（ 3.19）两式：（1）（2）3.5考虑下列双变量模型：模型1：模型2：（1）1 和1地OLS 估计量相同吗？它们地方差相等吗？（2）2 和2地OLS 估计量相同吗？它们地方差相等吗？3.6有人使用1980－1994 年度数据，研究汇率和相对价格地关系，得到如下结果：其中，Y＝马克对美元地汇率X＝美、德两国消费者价格指数（CPI）之比，代表两国地相对价格（1）请解释回归系数地含义；（2）X t 地系数为负值有经济意义吗？（3）如果我们重新定义X 为德国CPI与美国CPI之比，X 地符号会变化吗？为什么？3.7随机调查200 位男性地身高和体重，并用体重对身高进行回归，结果如下：其中Weight 地单位是磅（lb ），Height 地单位是厘米（cm）.（1）当身高分别为177.67cm、164.98cm、187.82cm 时，对应地体重地拟合值为多少？（2）假设在一年中某人身高增高了 3.81cm，此人体重增加了多少？3.8设有10 名工人地数据如下：X 10 7 10 5 8 8 6 7 9 10Y 11 10 12 6 10 7 9 10 11 10 其中X= 劳动工时，Y= 产量（1）试估计Y=α+βX + u（要求列出计算表格）；（2）提供回归结果（按标准格式）并适当说明；（3）检验原假设β=1.0.3.9用12 对观测值估计出地消费函数为Y=10.0+0.90X ，且已知=0.01，=200，=4000，试预测当X=250 时Y 地值，并求Y 地95%置信区间.文档收集自网络，仅用于个人学习3.10设有某变量（Y）和变量（X）1995—1999 年地数据如下:（3）试预测X=10 时Y 地值，并求Y 地95%置信区间.3.11根据上题地数据及回归结果，现有一对新观测值X ＝20，Y＝7.62，试问它们是否可能来自产生样本数据地同一总体？文档收集自网络，仅用于个人学习3.12有人估计消费函数，得到如下结果（括号中数字为t 值）：＝15 + 0.81 ＝0.98（2.7）（6.5）n=19（1）检验原假设：＝0（取显著性水平为5％）（2）计算参数估计值地标准误差；（3）求地95％置信区间，这个区间包括0 吗？3.13试用中国1985—2003 年实际数据估计消费函数：=α+β + u t其中：C代表消费，Y 代表收入.原始数据如下表所示，表中：Cr＝农村居民人均消费支出（元）Cu＝城镇居民人均消费支出（元）Y ＝国内居民家庭人均纯收入（元） Yr ＝农村居民家庭人均纯收入（元） Yu＝城镇居民家庭人均可支配收入（元） Rpop＝农村人口比重（%） pop＝历年年底我国人口总数（亿人）P＝居民消费价格指数（1985=100）Pr＝农村居民消费价格指数（1985=100）Pu＝城镇居民消费价格指数（1985=100）数据来源：《中国统计年鉴2004》使用计量经济软件，用国内居民人均消费、农村居民人均消费和城镇居民人均消费分别对各自地人均收入进行回归，给出标准格式回归结果；并由回归结果分析我国城乡居民消费行为有何不同.文档收集自网络，仅用于个人学习第四章多元线性回归模型4.1某经济学家试图解释某一变量Y 地变动.他收集了Y 和 5 个可能地解释变量～地观测值(共10 组)，然后分别作三个回归，结果如下(括号中数字为t 统计量)：文档收集自网络，仅用于个人学习( 1) = 51.5 + 3.21 R=0.63(3.45) (5.21)2) 33.43 + 3.67 + 4.62 + 1.21 R=0.75 文档收集自网络，仅用于个人学(3.61 )(2.56)(0.81) (0.22)3) 23.21 + 3.82 + 2.32 + 0.82 + 4.10 + 1.21(2.21 )(2.83)(0.62) (0.12) (2.10) (1.11)文档收集自网络，仅用于个人学习R=0.80 你认为应采用哪一个结果？为什么？4.2为研究旅馆地投资问题，我们收集了某地地1987-1995 年地数据来估计收益生产函数R=ALKe ，其中R=旅馆年净收益(万年) ，L=土地投入，K=资金投入， e 为自然对数地底.设回归结果如下(括号内数字为标准误差) ：文档收集自网络，仅用于个人学习= -0.9175 + 0.273lnL + 0.733lnK R=0.94(0.212) (0.135) (0.125)(1)请对回归结果作必要说明；( 2)分别检验α和β 地显著性；( 3)检验原假设：α =β = 0；4.3我们有某地1970-1987 年间人均储蓄和收入地数据，用以研究1970－1978 和1978 年以后储蓄和收入之间地关系是否发生显著变化. 引入虚拟变量后，估计结果如下(括号内数据为标准差) ：文档收集自网络，仅用于个人学习= -1.7502 + 1.4839D + 0.1504 - 0.1034D·R=0.9425 文档收集自网络，仅用于个人学习(0.3319) (0.4704) (0.0163) (0.0332)其中：Y=人均储蓄，X=人均收入，D= 请检验两时期是否有显著地结构性变化.4.4说明下列模型中变量是否呈线性，系数是否呈线性，并将能线性化地模型线性化.（1）（2）（3）4.5有学者根据某国19年地数据得到下面地回归结果：其中：Y=进口量（百万美元），X1 =个人消费支出（百万美元），X2 =进口价格/国内价格.（1）解释截距项以及X1和X2系数地意义；（2）Y 地总变差中被回归方程解释地部分、未被回归方程解释地部分各是多少？（3）进行回归方程地显著性检验,并解释检验结果；（4）对“斜率”系数进行显著性检验,并解释检验结果.4.6由美国46个州1992年地数据，Baltagi 得到如下回归结果：其中，C＝香烟消费（包/人年），P＝每包香烟地实际价格Y＝人均实际可支配收入（1）香烟需求地价格弹性是多少？它是否统计上显著？若是，它是否统计上异于-1？（2）香烟需求地收入弹性是多少？它是否统计上显著？若不显著，原因是什么？（3）求出.4.7有学者从209 个公司地样本，得到如下回归结果（括号中数字为标准误差）：其中，Salary＝CEO 地薪金Sales＝公司年销售额roe＝股本收益率（％）ros＝公司股票收益请分析回归结果.4.8为了研究某国1970－1992 期间地人口增长率，某研究小组估计了下列模型：其中：Pop＝人口（百万人），t＝趋势变量，.（1）在模型 1 中，样本期该地地人口增长率是多少？（2）人口增长率在1978 年前后是否显著不同？如果不同，那么1972－1977和1978－1992 两时期中，人口增长率各是多少？文档收集自网络，仅用于个人学习4.9设回归方程为Y= β0+β1X1+β2X2+β3X3+ u, 试说明你将如何检验联合假设：β1= β2 和β3 = 1 .文档收集自网络，仅用于个人学习4.10下列情况应引入几个虚拟变量，如何表示？（1）企业规模：大型企业、中型企业、小型企业；（2）学历：小学、初中、高中、大学、研究生.4.11在经济发展发生转折时期，可以通过引入虚拟变量来表示这种变化.例如，研究进口消费品地数量Y 与国民收入X 地关系时，数据散点图显示1979 年前后明显不同.请写出引入虚拟变量地进口消费品线性回归方程.文档收集自网络，仅用于个人学习4.12柯布－道格拉斯生产函数其中：GDP=地区国内生产总值（亿元）K=资本形成总额（亿元）L= 就业人数（万人）P=商品零售价格指数（上年＝100）试根据中国2003 年各省数据估计此函数并分析结果.数据如下表所示第五章模型地建立与估计中地问题及对策5.1判断题（判断对错；如果错误，说明理由）（1）尽管存在严重多重共线性，普通最小二乘估计量仍然是最佳线性无偏估计量（BLUE ）.（2）如果分析地目地仅仅是为了预测，则多重共线性并无妨碍. （3）如果解释变量两两之间地相关系数都低，则一定不存在多重共线性. （4）如果存在异方差性，通常用地t 检验和 F 检验是无效地. （5）当存在自相关时，OLS 估计量既不是无偏地，又不是有效地.（6）消除一阶自相关地一阶差分变换法假定自相关系数必须等于 1. （7）模型中包含无关地解释变量，参数估计量会有偏，并且会增大估计量地方差，即增大误差.（8）多元回归中，如果全部“斜率”系数各自经t 检验都不显著，则R2值也高不了.（9）存在异方差地情况下，OLS 法总是高估系数估计量地标准误差.（10）如果一个具有非常数方差地解释变量被（不正确地）忽略了，那么OLS 残差将呈异方差性.5.2考虑带有随机扰动项地复利增长模型：Y 表示GDP，Y0是Y 地基期值，r 是样本期内地年均增长率，t 表示年份，t＝1978，⋯,2003.文档收集自网络，仅用于个人学习试问应如何估计GDP 在样本期内地年均增长率？5.3 检验下列情况下是否存在扰动项地自相关 .（1） DW=0.81，n=21，k=3（2）DW=2.25，n=15，k=2（3）DW=1.56，n=30，k=55.4有人建立了一个回归模型来研究我国县一级地教育支出：Y= β0+β1X1+β 2X2+β3X3+u其中：Y，X1，X2 和X3分别为所研究县份地教育支出、居民人均收入、学龄儿童人数和可以利用地各级政府教育拨款.文档收集自网络，仅用于个人学习他打算用遍布我国各省、市、自治区地100 个县地数据来估计上述模型.（1）所用数据是什么类型地数据？（2）能否采用OLS 法进行估计？为什么？（3）如不能采用OLS 法，你认为应采用什么方法？5.5试从下列回归结果分析存在问题及解决方法：（1）= 24.7747 + 0.9415 - 0.0424 R=0.9635SE：（6.7525）（0.8229）（0.0807）其中：Y=消费，X2=收入，X3=财产，且n=5000 （2）= 0.4529 - 0.0041t R=0.5284t：（-3.9606） DW=0.8252其中Y= 劳动在增加值中地份额，t=时间该估计结果是使用1949-1964 年度数据得到地.5.6工资模型：wi＝b0＋b1Si＋b2Ei＋b3Ai＋b4Ui＋ui其中Wi＝工资，Si＝学校教育年限，Ei＝工作年限，Ai＝年龄，Ui＝是否参加工会.在估计上述模型时，你觉得会出现什么问题？如何解决？5.7你想研究某行业中公司地销售量与其广告宣传费用之间地关系.你很清楚地知道该行业中有一半地公司比另一半公司大，你关心地是这种情况下，什么估计方法比较合理.假定大公司地扰动项方差是小公司扰动项方差地两倍.文档收集自网络，仅用于个人学习（1）若采用普通最小二乘法估计销售量对广告宣传费用地回归方程（假设广告宣传费是与误差项不相关地自变量），系数地估计量会是无偏地吗？是一致地吗？是有效地吗？文档收集自网络，仅用于个人学习（2）你会怎样修改你地估计方法以解决你地问题？（3）能否对原扰动项方差假设地正确性进行检验？5.8考虑下面地模型其中GNP＝国民生产总值，M ＝货币供给. （1）假设你有估计此模型地数据，你能成功地估计出模型地所有系数吗？说明理由.（2）如果不能，哪些系数可以估计？（3）如果从模型中去掉这一项，你对（1）中问题地答案会改变吗？（4）如果从模型中去掉这一项，你对（1）中问题地答案会改变吗？5.9采用美国制造业1899－1922年数据，Dougherty得到如下两个回归结果：（1）（2）其中：Y＝实际产出指数，K＝实际资本投入指数，L ＝实际劳动力投入指数，t＝时间趋势（1）回归式（1）中是否存在多重共线性？你是如何得知地？（2）回归式（1）中，logK 系数地预期符号是什么？回归结果符合先验预期吗？为什么会这样？（3）回归式（1）中，趋势变量在其中起什么作用？（4）估计回归式（2）背后地逻辑是什么？（5）如果（1）中存在多重共线性，那么（2）式是否减轻这个问题？你如何得知？（6）两个回归地R2可比吗？说明理由.5.10有人估计了下面地模型：其中：C＝私人消费支出，GNP＝国民生产总值，D＝国防支出假定，将（1）式转换成下式：使用1946－1975数据估计（1）、（2）两式，得到如下回归结果（括号中数字为标准误差）：1）关于异方差，模型估计者做出了什么样地假定？你认为他地依据是什么？2）比较两个回归结果.模型转换是否改进了结果？也就是说，是否减小了估计标准误差？说明理由.5.11设有下列数据：RSS1＝55，K ＝4，n1＝30RSS3＝140，K ＝4，n3＝30 请依据上述数据，用戈德佛尔德－匡特检验法进行异方差性检验（5％显著性水平）.5.12考虑模型（1）也就是说，扰动项服从AR （2）模式，其中是白噪声.请概述估计此模型所要采取地步骤.5.13对第 3 章练习题 3.13 所建立地三个消费模型地结果进行分析：是否存在序列相关问题？如果有，应如何解决？5.14为了研究中国农业总产值与有效灌溉面积、化肥施用量、农作物总播种面积、受灾面积地相互关系，选31 个省市2003 年地数据资料，如下表所示：文档收集自网络，仅用于个人学习表中：Y＝农业总产值（亿元，不包括林牧渔）X1＝有效灌溉面积（千公顷）X2＝化肥施用量（万吨）X23＝化肥施用量（公斤/亩）X3＝农作物总播种面积（千公顷）X4＝受灾面积（千公顷）（1）回归并根据计算机输出结果写出标准格式地回归结果；（2）模型是否存在问题？如果存在问题，是什么问题？如何解决？第六章动态经济模型：自回归模型和分布滞后模型6.1判断题（判断对错；如果错误，说明理由）（1）所有计量经济模型实质上都是动态模型.（2）如果分布滞后系数中，有地为正有地为负，则科克模型将没有多大用处. （3）若适应预期模型用OLS 估计，则估计量将有偏，但一致. （4）对于小样本，部分调整模型地OLS 估计量是有偏地.（5）若回归方程中既包含随机解释变量，扰动项又自相关，则采用工具变量法，将产生无偏且一致地估计量.（6）解释变量中包括滞后因变量地情况下，用德宾－沃森d 统计量来检测自相关是没有实际用处地.6.2用OLS 对科克模型、部分调整模型和适应预期模型分别进行回归时，得到地OLS 估计量会有什么样地性质？文档收集自网络，仅用于个人学习6.3简述科克分布和阿尔蒙多项式分布地区别.6.4考虑模型假设相关.要解决这个问题，我们采用以下工具变量法：首先用对和回归，得到地估计值，然后回归其中是第一步回归（对和回归）中得到地.（1）这个方法如何消除原模型中地相关？（2）与利维顿采用地方法相比，此方法有何优点？6.5设其中：M＝对实际现金余额地需求，Y*＝预期实际收入，R*＝预期通货膨胀率假设这些预期服从适应预期机制：其中和是调整系数，均位于0和1之间.（1）请将M t 用可观测量表示；（2）你预计会有什么估计问题？6.6考虑分布滞后模型假设可用二阶多项式表示诸如下：若施加约束＝＝0，你将如何估计诸系数（，i=0,1, (4)6.7为了研究设备利用对于通货膨胀地影响，T. A.吉延斯根据1971年到1988年地美国数据获得如下回归结果：文档收集自网络，仅用于个人学习其中：Y＝通货膨胀率（根据GNP 平减指数计算）X t＝制造业设备利用率X t－1 ＝滞后一年地设备利用率1）设备利用对于通货膨胀地短期影响是什么？长期影响又是什么？(2)每个斜率系数是统计显著地吗？(3)你是否会拒绝两个斜率系数同时为零地原假设？将利用何种检验？6.8考虑下面地模型：Y t = α+β(W0X t+ W1X t-1 + W2X t-2 + W3X t-3)+u t 请说明如何用阿尔蒙滞后方法来估计上述模型(设用二次多项式来近似) .6.9下面地模型是一个将部分调整和适应预期假说结合在一起地模型：Y t*= βX t+1eY t-Y t-1 = δ(Y t*- Y t-1) + u tX t+1e- X t e= (1-λ)( X t - X t e)；t=1，2，⋯， n式中Y t*是理想值，X t+1e和X t e是预期值.试推导出一个只包含可观测变量地方程，并说明该方程参数估计方面地问题.文档收集自网络，仅用于个人学习第七章时间序列分析7.1单项选择题（1）某一时间序列经一次差分变换成平稳时间序列，此时间序列称为（）地.A．1 阶单整B．2阶单整C．K 阶单整D．以上答案均不正确文档收集自网络，仅用于个人学习（2）如果两个变量都是一阶单整地，则（）.A ．这两个变量一定存在协整关系B．这两个变量一定不存在协整关系C．相应地误差修正模型一定成立D．还需对误差项进行检验文档收集自网络，仅用于个人学习（3）如果同阶单整地线性组合是平稳时间序列，则这些变量之间关系是（） .A. 伪回归关系B.协整关系C.短期均衡关系D. 短期非均衡关系（4）．若一个时间序列呈上升趋势，则这个时间序列是（）.A ．平稳时间序列B．非平稳时间序列C．一阶单整序列 D. 一阶协整序列7.2请说出平稳时间序列和非平稳时间序列地区别，并解释为什么在实证分析中确定经济时间序列地性质是十分必要地.文档收集自网络，仅用于个人学习7.3什么是单位根？7.4Dickey－Fuller（DF）检验和Engle－Granger（EG）检验是检验什么地？文档收集自网络，仅用于个人学习7.5什么是伪回归？在回归中使用非均衡时间序列时是否必定会造成伪回归？7.6由1948－1984 英国私人部门住宅开工数（X）数据，某学者得到下列回归结果：注：5％临界值值为-2.95，10％临界值值为-2.60. （1）根据这一结果，检验住宅开工数时间序列是否平稳.（2）如果你打算使用t 检验，则观测地t 值是否统计显著？据此你是否得出该序列平稳地结论？（3）现考虑下面地回归结果：请判断住宅开工数地平稳性.7.7由1971-I 到1988-IV 加拿大地数据，得到如下回归结果；A.B.C.其中，M1＝货币供给，GDP=国内生产总值，e t＝残差（回归A）（1）你怀疑回归 A 是伪回归吗？为什么？（2）回归 B 是伪回归吗？请说明理由.（3）从回归 C 地结果，你是否改变（1）中地结论，为什么？（4）现考虑以下回归：这个回归结果告诉你什么？这个结果是否对你决定回归 A 是否伪回归有帮助？7.8 检验我国人口时间序列地平稳性，数据区间为1949－2003 年.单位：万人7.9对中国进出口贸易进行协整分析，如果存在协整关系，则建立E CM 模型.1951－2003 年中国进口（im ）、出口（ex）和物价指数（pt，商品零售物价指数）时间序列数据见下表.因为该期间物价变化大，特别是改革开放以后变化更为激烈，所以物价指数也作为一个解释变量加入模型中.为消除物价变动对进出口数据地影响以及消除进出口数据中存在地异方差，定义三个变量如下：文档收集自网络，仅用于个人学习第八章联立方程模型8.1判断题（判断对错；如果错误，说明理由）（1）OLS 法适用于估计联立方程模型中地结构方程.（2）2SLS 法不能用于不可识别方程.（3）估计联立方程模型地2SLS 法和其它方法只有在大样本地情况下，才能具有我们期望地统计性质 .(4) 联立方程模型作为一个整体，不存在类似 R 2这样地拟合优度测度 .(5) 如果要估计地方程扰动项自相关或存在跨方程地相关， 则 2SLS 法和其它估 计结构方程地方法都不能用 .(6) 如果一个方程恰好识别，则 ILS 和 2SLS 给出相同结果 .8.2 单项选择题1) 结构式模型中地方程称为结构方程 .在结构方程中， 解释变量可以是前定变3) 如果联立方程模型中某个结构方程包含了模型中所有地变量，则这个方程5)当一个结构式方程为恰好识别时，这个方程中内生解释变量地个数( A ．与被排除在外地前定变量个数正好相等 B ．小于被排除在外地前定变量个数 C ．大于被排除在外地前定变量个数D ．以上三种情况都有可能发生 文档收集自网络，仅用于个人学习6) 简化式模型就是把结构式模型中地内生变量表示为 ( ).A. 外生变量和内生变量地函数关系B.前定变量和随机误差项地模型C.滞后变量和随机误差项地模型 D.外生变量和随机误差项地模量，也可以是 ( ).文档收集自网络，仅用于个人学习 A. 外生变量 B.滞后变量2)前定变量是 ( )地合称 .A.外生变量和滞后内生变量C.内生变量D. 外生变量和内生变量 C.外生变量和虚拟变量 D. 解释变量和被解释变量( ).A. 恰好识别B.不可识别 (4) 下面说法正确地是( ).A.内生变量是非随机变量 C.外生变量是随机变量 C.过度识别 D.不确定B. 前定变量是随机变量个人收集整理勿做商业用途型7) 对联立方程模型进行参数估计地方法可以分两类，即：( ).A.间接最小二乘法和系统估计方法B.单方程估计法和系统估计方法个人收集整理勿做商业用途C.单方程估计法和二阶段最小二乘法D.工具变量法和间接最小二乘法（8）在某个结构方程过度识别地条件下，不适用地估计方法是（）.A. 间接最小二乘法B.工具变量法C.二阶段最小二乘法D.有限信息极大似然估计法8.3行为方程和恒等式有什么区别？8.4如何确定模型中地外生变量和内生变量？8.5考虑下述模型：C t = α + β D t +u t I t = γ + δD t-1 + νt D t = C t +I t + Z t ；t=1 ，2，⋯，n其中 C = 消费支出，D= 收入，I = 投资，Z = 自发支出. C、I 和D是内生变量.试写出消费支出地简化型方程，并研究各方程地识别问题.8.6考虑下述模型：Y t = C t + I t +G t +X tC t = β 0 + β 1D t + β2C t-1 + u tD t = Y t –T tI t = α0 + α1Y t + α2R t-1 +νt 模型中各方程是正规化方程，u t、νt为扰动项.（1）请指出模型中地内生变量、外生变量和前定变量.（2）写出用2SLS法进行估计时，每个阶段中要估计地方程.8.7下面是一个简单地美国宏观经济模型（1960－1999）其中C=实际私人消费，I= 实际私人总投资，G=实际政府支出，Y ＝实际GDP，M= 当年价M2，R=长期利率；P＝消费价格指数.内生变量：C，I，R，Y 前定变量：C t-1，I t-1，M t-1，P t，R t-1 和G t.（1）应用识别地阶条件，决定各方程地识别状态；（2）你打算用什么方法来估计可识别行为方程？8.8假设有如下计量经济模型：其中，Y＝国民收入，I=净资本形成，C=个人消费，Q ＝利润，P=生活费用指数，R= 工业劳动生产率1）写出模型地内生变量、外生变量和前定变量；个人收集整理勿做商业用途（2）用识别地阶条件确定各方程地识别状态；（3）此模型中是否有可以用ILS 法估计地方程？如有，请指出；（4）写出用2SLS 法进行估计时，每个阶段中要估计地方程. 8.9考虑下述模型：消费方程：C t=α0 +α 1Y t +α2C t-1 +u①投资方程：I t=β0 +β1Y t +β2I t –1+u2t②进口方程：M t = 0 + 1Y t + u3t ③Y t = C t+ I t + G t + X t - M t模型中各方程是正规化方程，u 1t, ⋯u3t为扰动项.（1）请指出模型中地内生变量、外生变量和前定变量.（2）利用阶条件识别各行为方程.（3）写出用3SLS 进行估计时地步骤.8.10考察下述国民经济地简单模型式中，C为消费，Y 为国民收入，I 为投资，R为利率.设样本容量n 为20，已算得中间结果为：（1）判别模型中消费方程地识别状态；（2）用间接最小二乘法求消费方程结构式系数；（3）将采用哪种方法估计投资方程?为什么?（不必计算）8.11由联立方程模型；得到其简化式如下：（1）两结构方程可识别吗？（2）如果知道，识别情况有何变化？（3）若对简化式进行估计，结果如下：个人收集整理勿做商业用途试求出结构参数地值，并说明如何检验原假设个人收集整理勿做商业用途版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理。

第十三章面板数据模型一简单题1、简述面板数据模型的优点和局限性它能综合利用样本信息，同时反映应变量在截面和时序两个方向上的变化规律及特征。

由于面板数据模型在经济定量分析中，起着只用截面或只用时序数据模型不可替代的独特优点，而具有很高的应用价值。

总之：1．增加了样本容量；2. 可多层面分析经济问题局限性：模型设定错误与数据手机不慎引起较大的偏差；研究截面或者平行数据时，由于样本非随机性造成观测值的偏差，从而导致模型选择上的偏差。

2、你是如何理解面板数据的？在经济领域中，同时具有截面与时序特征的数据很多。

如统计年鉴中提供的各地区或各国的若干系列的年度（季度或月度）经济总量数据；在企业投资分析中，要用到多个企业若干指标的月度或季度时间序列数据；在城镇居民消费分析中，要用到不同省市反映居民消费和收入的年度时序数据。

我们将上述的企业、或地区等统称为个体，从行的方向看，是由若干个体在某个时期构成的截面观察值（截面样本），从列的方向看，是各时间序列。

这种具有三维（截面、时期、变量）信息的数据结构称为面板。

这是“面板”数据的由来，面板数据也称为时序截面数据或混合数据（Pooled Data）。

3、简述建立面板数据模型的过程。

（1）建立面板数据对象，即建立工作文件；（2）面板时序变量平稳性检验；（3）协整检验；（4）模型识别；（5）建立模型；（6）结论。

二填空题1、GDP界面变量是一维变量，面板变量为三维变量。

2、面板数据模型是无斜率系数非齐性、而截距齐性的模型。

3、面板数据模型识别包括效应模型识别和具体模型识别。

4、建立面板数据模型之前，要对面板变量进行平稳性检验和协整检验。

第十二章向量自回归(VAR)模型和向量误差修正(VEC)模型一简答题1、VAR模型的特点VAR模型不以经济理论为指导，它根据样本数据统计特征建模。

VAR模型对参数不施加零约束（如t检验），故称其为无约束VAR模型。

VAR模型的解释变量中不含t期变量，所有与线性联利方程组模型有关的问题均不存在。

第8章练习5证明:对方程εβtttX Y1+=两边同时减去Yt 1-，得：εβt t ttYX Y11+-=∆-然后对该式等号右边加上再减去一个Xt 1-β，得：εβββt t t t t t XXYX Y 1111+-+-=∆---()εββtt t tX YX 111+--=--∆将第二个方程εαt t tX X21+∆=∆-代入，得：()()εεβαβtt t t t t X Y X Y 11121+--+∆=∆--- ()εεβββαttt t t X Y X21111++--∆=---()εαβδtt t t X Y X +-+∆=---1111其中，βαα=1，1-=δ，εεεβt t t 21+=第8章练习8（1） 解：根据Eview 软件操作得：对1978-2007年中国货物进、出口额的自然对数系列LX ， LM 的单位根检验分别如下： 对LX 的单位根检验：Null Hypothesis: LX has a unit root Exogenous: NoneLag Length: 2 (Fixed)t-Statistic Prob.*Augmented Dickey-Fuller test statistic 3.660835 0.9998Test critical values: 1% level -2.6534015% level -1.95385810% level -1.609571*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(LX)Method: Least SquaresDate: 05/28/11 Time: 12:13Sample (adjusted): 1981 2007Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.LX(-1) 0.022104 0.006038 3.660835 0.0012D(LX(-1)) 0.089362 0.198210 0.450844 0.6561D(LX(-2)) -0.056822 0.179525 -0.316512 0.7544R-squared 0.165948 Mean dependent var 0.155844Adjusted R-squared 0.096444 S.D. dependent var 0.094091S.E. of regression 0.089439 Akaike info criterion -1.886086Sum squared resid 0.191983 Schwarz criterion -1.742104Log likelihood 28.46216 Hannan-Quinn criter. -1.843273Durbin-Watson stat 2.075404根据上表得”Augmented Dickey-Fuller test statistics”的数值为 3.660835，大于5% critical values:的数值-1.953858，即3.660835>-1.953858。

第8章练习5证明:对方程εβtttX Y1+=两边同时减去Yt 1-，得：εβt t ttYX Y11+-=∆-然后对该式等号右边加上再减去一个Xt 1-β，得：εβββt t t t t t XXYX Y 1111+-+-=∆---()εββtt t tX YX 111+--=--∆将第二个方程εαt t tX X21+∆=∆-代入，得：()()εεβαβtt t t t t X Y X Y 11121+--+∆=∆--- ()εεβββαttt t t X Y X21111++--∆=---()εαβδtt t t X Y X +-+∆=---1111其中，βαα=1，1-=δ，εεεβt t t 21+=第8章练习8（1） 解：根据Eview 软件操作得：对1978-2007年中国货物进、出口额的自然对数系列LX ， LM 的单位根检验分别如下： 对LX 的单位根检验：Null Hypothesis: LX has a unit root Exogenous: NoneLag Length: 2 (Fixed)t-Statistic Prob.*Augmented Dickey-Fuller test statistic 3.660835 0.9998Test critical values: 1% level -2.6534015% level -1.95385810% level -1.609571*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(LX)Method: Least SquaresDate: 05/28/11 Time: 12:13Sample (adjusted): 1981 2007Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.LX(-1) 0.022104 0.006038 3.660835 0.0012D(LX(-1)) 0.089362 0.198210 0.450844 0.6561D(LX(-2)) -0.056822 0.179525 -0.316512 0.7544R-squared 0.165948 Mean dependent var 0.155844Adjusted R-squared 0.096444 S.D. dependent var 0.094091S.E. of regression 0.089439 Akaike info criterion -1.886086Sum squared resid 0.191983 Schwarz criterion -1.742104Log likelihood 28.46216 Hannan-Quinn criter. -1.843273Durbin-Watson stat 2.075404根据上表得”Augmented Dickey-Fuller test statistics”的数值为 3.660835，大于5% critical values:的数值-1.953858，即3.660835>-1.953858。

第八章 联立方程的识别和估计一、习题（一）简答题1．内生变量；2．外生变量；3．前定变量；4．（1）行为方程；（2）技术方程；（3）制度方程；（4）恒等式；5．（1）联立方程系统的结构型； （2）联立方程组的简化型；（二）计算题1．某联立方程计量经济学模型有3个方程、3个内生变量(,,)y y y 123、3个外生变量(,,)x x x 123和样本观测值始终为1的虚变量C ，样本容量为n 。

其中第二个方程为 y x y x 201123332=++++ααααμ⑴ 能否采用OLS 方法估计该结构方程？为什么？⑵ 该方程是否可以识别？2．下列为一完备的联立方程计量经济模型tt t t t t t tt t t G I C Y Y I C Y C ++=++=+++=-21011210μββμααα其中C 为居民消费总额、I 为投资总额、Y 为国内生产总值、t G 为政府消费总额，样本取自1978—2000年。

⑴ 说明：对于消费方程，用IV 、ILS 、2SLS 方法分别估计，参数估计结果是等价的。

⑵ 说明：对于投资方程，能否用IV 、ILS 方法估计？为什么？⑶ 对于该联立方程计量经济模型，如果采用2SLS 估计指出其优缺点。

⑷ 如果该模型的每个结构方程的随机项具有同方差性和序列不相关性，而不同结构方程的随机项之间具有同期相关性。

写出它们的方差协方差矩阵。

3．投资函数模型t t t t Y Y I μβββ+++=-1210为一完备的联立方程计量经济模型中的一个方程，模型系统包含的内生变量为C （居民消费总额）、I （投资总额）和Y （国内生产总值），先决变量为t G （政府消费）、1-t C 和1-t Y 。

样本容量为n 。

⑴ 可否用狭义的工具变量法估计该方程？为什么？⑵ 如果采用2SLS 估计该方程，分别写出2SLS 估计量和将它作为一种工具变量方法的估计量的矩阵表达式；⑶ 如果采用GMM 方法估计该投资函数模型，写出一组等于0的矩条件。

第八章1. 格兰杰因果关系检验的基本思路是，如果变量x是y的原因，则在给定x和y的信息集（要求必须是平稳的时间序列资料）的情况下，如果利用x的信息比不用能够更好地预测y的值，表明的x变化引起了y的变化，二者存在着格兰杰意义上的因果关系。

这意味着以下两点成立：第一，x应该有助于预测y，即在y对它自身的滞后值进行自回归的方程中，如果把x作为独立解释变量加到方程中去，应该能够更好地提高方程的解释能力；第二，y不应该有助于预测x，原因是，如果x有助于预测y，y又有助于预测x，则可能存在另外的一个（组）变量，它（们）是x和y变化的共同原因；x和y之间不存在格兰杰意义上的因果关系。

2. 从前进法和后退法的思想及方法，以及我们看到它们的不足，人们比较自然地想构造一种方法，吸收前进法和后退法的优点，克服它们的不足，把两者结合起来，这就有了逐步回归的思想。

逐步回归的基本思想是“有进有出”。

具体做法是将变量一个一个引入，引入变量的条件是其偏F统计量或t统计量经检验是显著的。

即每引入一个自变量后，对已经被选入的变量要进行逐个检验，当原引入的变量由于后面变量的引入而变得不再显著时，要将其剔除。

引入一个变量或从回归方程中剔除一个变量，为逐步回归的一步，每一步都要进行偏F检验或t检验（二者等价），以确保每次引入新的变量之前回归方程中只包含显著的变量。

这个过程反复进行，直到既无显著的自变量选入回归方程，也无不显著自变量从回归方程中剔除为止。

这样就保证了最后所得的回归子集是“最优”回归子集。

在逐步回归法中需要注意的是引入和剔除自变量的显著性水平α应该有所不同，一般要求引入自变量的显著性水平α1小于剔除自变量的显著性水平α2，否则可能产生“死循环”的现象。

就是说，如果引入自变量的显著性水平α1不小于剔除自变量的显著性水平2α时，如果某个自变量的显著性水平（P值）在α1和α2之间，那么，这个变量就会被引入、剔除、再引入、再剔除……，循环往复，以至无穷。

第八章答案8.1 Sen 和Srivastava （1971）在研究贫富国之间期望寿命的差异时，利用101个国家的数据，建立了如下的回归模型：2.409.39ln3.36((ln 7))i i i i Y X D X =-+--(4.37) (0.857) (2.42) R 2=0.752其中：X 是以美元计的人均收入；Y 是以年计的期望寿命；Sen 和Srivastava 认为人均收入的临界值为1097美元（ln10977=），若人均收入超过1097美元，则被认定为富国；若人均收入低于1097美元，被认定为贫穷国。

括号内的数值为对应参数估计值的t-值。

1）解释这些计算结果。

2）回归方程中引入()ln 7i i D X -的原因是什么？如何解释这个回归解释变量？ 3）如何对贫穷国进行回归？又如何对富国进行回归？ 4）从这个回归结果中可得到的一般结论是什么？ 练习题8.1参考解答： 1. 结果解释依据给定的估计检验结果数据，对数人均收入对期望寿命在统计上并没有显著影响，截距和变量()ln 7i i D X -在统计上对期望寿命有显著影响；同时，()()2.40 3.3679.39 3.36ln ((ln 7)) 1 2.409.39ln 0 i i i i i i i X D X D Y X D ⎧-+⨯+---==⎨-+=⎩富国时穷国时 表明贫富国之间的期望寿命存在差异。

2. 回归方程中引入()ln 7i i D X -的原因是从截距和斜率两个方面考证收入因素对期望寿命的影响。

这个回归解释变量可解释为对期望寿命的影响存在截距差异和斜率差异的共同因素。

3. 对穷国进行回归时，回归模型为12ln 1097i i i i i i Y X Y X αα=+≤，其中，为美元时的寿命； 对富国进行回归时，回归模型为12ln 1097i i i i i i Y X Y X ββ=+>，其中，为美元时的寿命；4. 一般的结论为富国的期望寿命药高于穷国的期望寿命，并且随着收入的增加，在平均意义上，富国的期望寿命的增加变化趋势优于穷国，贫富国之间的期望寿命的确存在显著差异。

计量经济学各章习题及答案第一章习题一、单项选择1.( ) 是经济计量学的主要开拓者人和奠基人。

A.费歇（fisher） B .费里希（frisch）C.德宾（durbin）D.戈里瑟（glejer）2.随机方程又称为（）。

A．定义方程 B.技术方程C．行为方程 D.制度方程3.计量经济分析工作的研究对象是（）。

A.社会经济系统B.经济理论C.数学方法在经济中的应用D.经济数学模型二、多项选择1.经济计量学是下列哪些学科的统一（）。

A.经济学B.统计学C.计量学D.数学E.计算机2.对一个独立的经济计量模型来说，变量可分为（）、A.内生变量B独立变量C外生变量D.相关变量E虚拟变量3.经济计量学分析工作的工作步骤包括（）。

A设定模型B估计参数C检验模型D应用模型E收集数据三、名词解释1.时序数据2.横截面数据3.内生变量4.解释变量5.模型6.外生变量第一章习题答案一、单项选择B\C\A二、多项选择1C\D 2A\C 3A\B\C\D三、名词解释1.时序数据指同一指标按时间顺序记录的数据列，在同一数据列中的数据必须是同口径的，有可比性2.横截面数据同一时间，在不同统计单位的相同统计指标组成的数据列，要求统计的时间相同，不要求统计对象及范围相同。

要求数据统计口径和计算方法具有可比性 3.内生变量具有一定概率分布的随机变量，数据由模型本身决定 4.解释变量在模型中方程右边作为影响因素的变量，即自变量 5.模型对经济系统的数学抽象 6.外生变量非随机变量，取值由模型外决定，是求解模型时的已知数第二章习题一、单项选择1.一元线性回归分析中有TSS=RSS+ESS 。

则RSS 的自由度为（）。

A nB 1C n-1D n-22.一元线性会规中，0β∧、1β∧的值为（ ）∑∑---=∧2i)()(0X X Y Y X X ii ）（βXY 01∧∧-=ββ XY 10∧∧-=ββ∑∑---=∧2i)()(1X X Y Y X X ii ）（βY X =+∧∧10ββ∑∑---=∧2i)()(0X X Y Y X X ii ）（βXY 10∧∧+=ββ∑∑---=∧2i)()(1X X Y Y X X ii ）（β3．一元线性回归中，相关系数r=( ) A.∑∑∑----222)()()))(Y Y X X Y Y X X i i i i （（ B.∑∑∑----22)()())(Y Y X X Y Y X X iiii（ C ∑∑∑----22)()())(Y Y X XY Y X X iii i （ D∑∑∑---222)()()(Y Y X XY Y iii4.对样本相关系数r，以下结论中错误的是ABDC（ ）。

课后习题参考答案第二章教材习题与解析1、 判断下列表达式是否正确：y i =β0+β1x i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i ,i =1,2,⋯nE(y i |x i )=β0+β1x i +u i ,i =1,2,⋯n E(y i |x i )=β0+β1x i ,i =1,2,⋯nE(y i |x i )=β̂0+β̂1x i ,i =1,2,⋯ny i =β0+β1x i +u i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n y ̂i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n答案：对于计量经济学模型有两种类型，一是总体回归模型，另一是样本回归模型。

两类回归模型都具有确定形式与随机形式两种表达方式：总体回归模型的确定形式：X X Y E 10)|(ββ+= 总体回归模型的随机形式：μββ++=X Y 10样本回归模型的确定形式：X Y 10ˆˆˆββ+= 样本回归模型的随机形式：e X Y ++=10ˆˆββ 除此之外，其他的表达形式均是错误的2、给定一元线性回归模型：y =β0+β1x +u （1）叙述模型的基本假定；（2）写出参数β0和β1的最小二乘估计公式；（3）说明满足基本假定的最小二乘估计量的统计性质； （4）写出随机扰动项方差的无偏估计公式。

答案：（1）线性回归模型的基本假设有两大类，一类是关于随机误差项的，包括零均值、同方差、不序列相关、满足正态分布等假设；另一类是关于解释变量的，主要是解释变量是非随机的，如果是随机变量，则与随机误差项不相关。

（2）12ˆi iix yxβ=∑∑，01ˆˆY X ββ=- （3）考察总体的估计量，可从如下几个方面考察其优劣性：1）线性性，即它是否是另一个随机变量的线性函数； 2）无偏性，即它的均值或期望是否等于总体的真实值；3）有效值，即它是否在所有线性无偏估计量中具有最小方差；4）渐进无偏性，即样本容量趋于无穷大时，它的均值序列是否趋于总体真值； 5）一致性，即样本容量趋于无穷大时，它是否依概率收敛于总体的真值；6）渐进有效性，即样本容量趋于无穷大时，它在所有的一致估计量中是否具有最小的渐进方差。

第一章1．计量经济学是一门什么样的学科？答：计量经济学的英文单词是Econometrics，本意是“经济计量”，研究经济问题的计量方法，因此有时也译为“经济计量学”。

将Econometrics译为“计量经济学”是为了强调它是现代经济学的一门分支学科，不仅要研究经济问题的计量方法，还要研究经济问题发展变化的数量规律。

可以认为，计量经济学是以经济理论为指导，以经济数据为依据，以数学、统计方法为手段，通过建立、估计、检验经济模型，揭示客观经济活动中存在的随机因果关系的一门应用经济学的分支学科。

2．计量经济学与经济理论、数学、统计学的联系和区别是什么？答：计量经济学是经济理论、数学、统计学的结合，是经济学、数学、统计学的交叉学科（或边缘学科）。

计量经济学与经济学、数学、统计学的联系主要是计量经济学对这些学科的应用。

计量经济学对经济学的应用主要体现在以下几个方面：第一，计量经济学模型的选择和确定，包括对变量和经济模型的选择，需要经济学理论提供依据和思路；第二，计量经济分析中对经济模型的修改和调整，如改变函数形式、增减变量等，需要有经济理论的指导和把握；第三，计量经济分析结果的解读和应用也需要经济理论提供基础、背景和思路。

计量经济学对统计学的应用，至少有两个重要方面：一是计量经济分析所采用的数据的收集与处理、参数的估计等，需要使用统计学的方法和技术来完成；一是参数估计值、模型的预测结果的可靠性，需要使用统计方法加以分析、判断。

计量经济学对数学的应用也是多方面的，首先，对非线性函数进行线性转化的方法和技巧，是数学在计量经济学中的应用；其次，任何的参数估计归根结底都是数学运算，较复杂的参数估计方法，或者较复杂的模型的参数估计，更需要相当的数学知识和数学运算能力，另外，在计量经济理论和方法的研究方面，需要用到许多的数学知识和原理。

计量经济学与经济学、数学、统计学的区别也很明显，经济学、数学、统计学中的任何一门学科，都不能替代计量经济学，这三门学科简单地合起来，也不能替代计量经济学。