- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011-12-11
∴ w '( x m ) = ( u '( x m ) − p ( x m ) − p '( x m ) x m ) + 0 = − p '( x m ) x m > 0
15
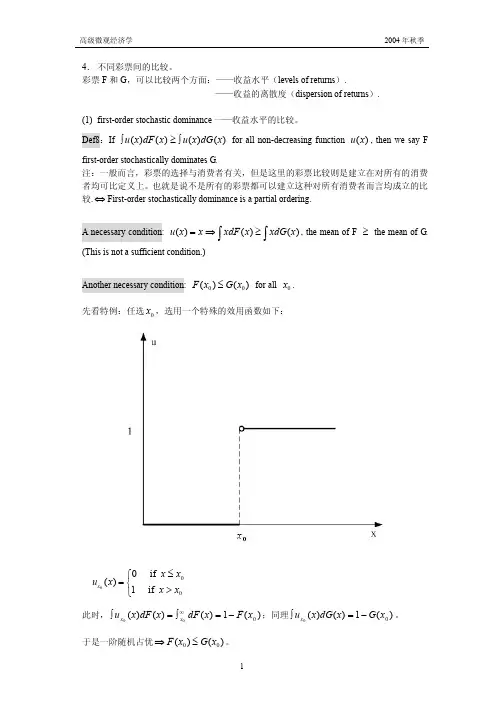
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
dw ≠ 0 ¡ 观点: d q m ¡ 前提: ™含质量变量的社会福利最大化模型 ™假定只有一个消费者,其有拟线性效用函数 ¡ 方法一:社会福利最大化模型 W (x,q)=CS+PS
方法一:社会福利最大化模型 W (x,q)=CS+PS 先考虑垄断者利润最大化: Max p ( x, q ) x − c ( x, q )
x ,q
在最优解( xm , qm)处必定满足 FOC,即 xm : ∂ p ( xm , q m ) ∂c ( xm , q m ) p ( xm , q m ) + xm = ∂x m ∂ xm (1) (2)
根据参数变化对最优值影响的比较静态分析 方法:有(2)式;并且,最优选择值y关于参 数c的导数的符号,仅依赖于目标函数关于y和c 的二阶偏导数。(在最大值前提下,分母小于 2011-12-11 10 0,故有(3)式。)
dp 三、比较静态分析: 关于 的表达式 dc ¡ 推导: dp ™其次,关于 度量的具体表达式 dc
17
∂p ( xm , q m ) ∂c ( xm , q m ) qm : xm = ∂q m ∂qm 2011-12-11
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
¡ 方法一:社会福利最大化模型 W (x,q)=CS+PS
再考虑在最优解( xm , qm)处的社会福利函数: w ( xm , q m ) = u ( xm , q m ) − c ( x m , q m ) 上式关于 xm , qm的导数为 xm : qm :
∂ π ( y( c ),c ) ∂y∂c dy 1 Q =− 2 = ' 2 " ∂ π ( y( c ),c ) ∂ y 2 p ( y ) + p ( y ) y dc
2
dp dp dy p( y) ∴ = = ' dc dy dc 2 p ( y ) + p" ( y ) y 1 = (4) " ' 2 + p ( y )y p ( y )
FOC : p( y ) + p' ( y ) y = c' ( y ) SOC : 2 p' ( y ) + p" ( y ) y < c "( y )
2011-12-11 3
2.1 垄断市场
一、垄断厂商的利润最大化 ¡ 关于FOC ™第一,MR(y*) = MC(y*) ™第二、FOC也可写成
2011-12-11
19
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
¡ 方法一:社会福利最大化模型 W (x,q)=CS+PS
由(4)出发,利用FOC中的(2),则(4)可写为 ∂w( xm , qm ) ∂u ( xm , qm ) ∂p( xm , qm ) = − xm (4 ' ) ∂qm ∂qm ∂qm 整理得 1 ∂w( xm , qm ) ∂ u ( x, q) = − p( x, q) |x= xm ,q =qm xm ∂qm ∂qm x ∂w( xm , qm ) ⇒ ≠0 ∂qm 2011-12-11
2011-12-11
∗ 厂商生产的边际成本为常数c。
24
2.2 价格歧视
一、一级价格歧视 3、模型分析 ¡ 意愿总支付的角度
于是,垄断者利润最大化问题为 M a x r − cx
r ,x
s .t . u ( x) = r ⇒ M a x u ( x ) − cx
r,x
F O C : u '( x ) = c 即 且有
∂u 令 : u = u ( x , q ), 且 > 0; ∂q c = c ( x , q ), 且
2011-12-11
∂c > 0. ∂q
16
w ( x , q )= C S + P S = u ( x , q ) − c( x , q )
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
¡ 含质量变量的社会福利最大化模型
Q e d > 1,
∴ p( y ) > c'( y )
4
2.1 垄断市场
¡ 关于FOC ™第三、因为MR(y)=p(y) + p’(y)y, 且p’(y)<0,
所以,MR(y) < p(y )。 ¡ 关于SOC 要求MR’(y) < MC’(y)。 具体分为两种情况: 之一:MR’(y) <0, MC’(y)>0; 之二:MR’(y) <0, MC’(y) <0, 且| MR’(y) |>| MC’(y) |。 → MR曲线必须从MC曲线上方穿过MC曲线。
2.1 垄断市场
dp 三、比较静态分析:关于 dc 的表达式 ¡ 意义 ¡ 推导
令 : M C =c ,于 是 , M ax
y
p ( y ) ⋅ y − cy p '( y ) ⋅ y + p ( y ) − c = 0 y* = y ( c ) π
*Leabharlann FOC : 解得= π ( y ( c ), c )
2011-12-11
∂w ( xm , q m ) ∂u ( xm , q m ) ∂ c ( x m , q m ) = − ∂xm ∂ xm ∂xm ∂w ( xm , q m ) ∂u ( x m , q m ) ∂ c ( xm , q m ) = − ∂q m ∂ qm ∂q m
(3) (4)
2011-12-11 5
2.1 垄断市场
二、两种特殊的情形 1、线性需求函数
如 p( y ) = a − by ⇒ TR = p( y ) y = ay − by 2 M R = a − 2bcy ⇒∗ ∗ p( y )与 M R ( y) 系 令 : M C = c, TC= cy , 由 M R = M C 得 a−c y* = 2b p* = a + c 2
2011-12-11
2011-12-11 11
'
三、比较静态分析
dp ¡ 例子:关于 d c
值 根据(4)式可具体计算以下两种特殊情况的 情况的 d p 值:
dc • 令:
p( y ) = a − by dp 1 = 有 dc 2 • 令 : y = p−b ed dp b = = 有 dc b − 1 ed − 1
dp y p ( y )( 1 + )= c ' ( y ) dy p 1 p ( y )( 1 − )= c ' ( y ) ed
¡ 在完全竞争市场,ed = ∞,故p=c’(y) ¡ 在垄断市场,ed > 1, 故 ' c 由上式可得 p ( y ) = ( y ) 1 1− ed
2011-12-11
dy ∂ 2 π ( y ( c ), c ) ∂ y ∂ c • = − 2 dc ∂ π ( y ( c ), c ) ∂ 2 y < 0 (2 ) (3)
2.1 垄断市场
dy ∂ 2 π ( y ( c ), c ) = s ig n = −1 且 s ig n dc ∂y∂c dp dp dy ⇒ = > 0 dc dy dc
2011-12-11 21
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
¡ 方法二:社会福利最大化模型 W (x,q)=CS+π
∂CS ( xm , qm ) 关于消费者剩余CS( xm , qm )项:必有 > 0 (3) ∂xm ∂CS ( xm , qm ) ∂CS ( xm , qm ) 但 符号不定,一般有 ≠ 0 (4) ∂qm ∂qm ∂w( xm , qm ) ⇒ 最后,由(1)和(3),有 > 0 (5) ∂xm ∂w( xm , qm ) 由(2)和(4),有 ≠ 0 (6) ∂qm
2011-12-11 22
第2章
非完全竞争市场
¡ 2.1 垄断市场 ¡ 2.2 价格歧视
2011-12-11
23
2.2 价格歧视
一、一级价格歧视 1、定义 2、影响 3、模型分析 ¡ 意愿总支付的角度
假定: ∗ 只分析一个消费者的情况,且有拟线性效用函数。 ∗ 垄断者选择一个总价格和产量的组合( r , x ),以获得更大 的利润。其中,r为消费者的(最大)意愿总支付。 显然,面对总价格r,消费者的选择是要么接受(r , x ), 要么放弃消费即x =0。
18
2.1 垄断市场
五、垄断厂商的产品质量和社会福利
¡ 方法一:社会福利最大化模型 W (x,q)=CS+PS
最后,由(3)出发,因为拟线性效用函数, 则(3)可写为 ∂w( xm , qm ) ∂c ( xm , qm ) = p ( xm , qm ) − ∂xm ∂xm 由(1) ∂p ( xm , qm ) =− xm > 0 ∂xm (3' )
2011-12-11
8
dp 三、比较静态分析:关于 的表达式 dc ¡ 推导:在最优点上有
p = p( y( c )) dp dp dy = dc dy dc
(1)
™首先,关于(1)式符号的判断。
具 体 的 , 有 dp • < 0 dy
2011-12-11 9
dp 三、比较静态分析: 关于 dc 的表达式