现代控制：由能控标准I型求传递函数

传递函数能控标准型传递函数能控标准型。

传递函数是描述线性时不变系统的输入和输出之间关系的数学表达式。

在控制系统中，传递函数是非常重要的概念，它可以帮助我们分析系统的性能、稳定性和动态响应。

本文将围绕传递函数能控标准型展开讨论，介绍其定义、特点以及在控制系统中的应用。

传递函数能控标准型是指系统的传递函数可以通过控制输入来实现系统的稳定性和性能要求。

在控制系统设计中，我们通常希望系统能够对不同的输入信号做出合适的响应，并且在一定的时间内实现稳定。

传递函数能控标准型的出现，正是为了满足这一需求。

传递函数能控标准型的定义是系统传递函数的分子次数小于或等于分母次数，并且系统的传递函数的根全部位于单位圆内。

这个定义的核心是系统的传递函数的特征，通过对传递函数的分子、分母次数以及根的位置进行分析，我们可以判断系统是否满足能控标准型。

传递函数能控标准型的特点包括，一是系统的传递函数是严格因果的，即系统的输出只取决于过去的输入；二是系统的传递函数是稳定的，即系统的输出在有限时间内有界；三是系统的传递函数是最小相位的，即系统的相位响应是最小的。

这些特点保证了系统在控制输入的作用下能够实现稳定的性能要求。

在控制系统中，传递函数能控标准型具有重要的应用价值。

首先，通过对系统传递函数进行分析，我们可以判断系统是否满足能控标准型，从而为系统的稳定性和性能提供依据。

其次，传递函数能控标准型可以作为控制系统设计的指导原则，帮助我们选择合适的控制策略和参数。

最后，传递函数能控标准型还可以用于系统的故障诊断和故障恢复，通过对系统传递函数的变化进行监测，我们可以及时发现系统的故障并采取相应的措施。

总之，传递函数能控标准型是控制系统中的重要概念，它对系统的稳定性和性能具有重要的影响。

通过对传递函数能控标准型的理解和应用，我们可以更好地设计和分析控制系统，从而实现对系统的有效控制和管理。

希望本文的介绍能够帮助读者更好地理解传递函数能控标准型的概念和应用。

传递函数能控标准型传递函数是描述线性时不变系统输入和输出之间关系的数学工具，它在控制系统理论中起着至关重要的作用。

在控制系统设计中，我们常常需要将系统的动态特性用数学模型来描述，而传递函数正是这样一种数学模型。

传递函数能控标准型是一种特殊的传递函数形式，它在控制系统设计和分析中具有重要的应用价值。

传递函数能控标准型通常具有以下的形式：\[G(s) = \frac{k}{s(Ts+1)}\]其中，\(k\) 为系统的增益，\(T\) 为系统的时间常数。

这种形式的传递函数在控制系统理论中具有重要的意义，它可以帮助我们分析系统的稳定性、动态特性和频域特性，从而指导控制系统的设计和调节。

传递函数能控标准型的特点是具有一个一阶惯性环节和一个零点，这种形式的传递函数在控制系统中是非常常见的。

通过对传递函数进行分析，我们可以得到系统的阶跃响应、脉冲响应和频率响应等重要性能指标，从而对系统的性能进行评价和改进。

在控制系统设计中，我们经常会遇到需要将系统的传递函数转化为能控标准型的形式。

这样做的目的是为了方便系统分析和设计，能够更清晰地了解系统的动态特性和稳定性。

同时，能控标准型也是许多控制系统设计方法的基础，比如根轨迹法、频率法等。

通过对传递函数进行变换和调节，我们可以将系统的传递函数变换为能控标准型的形式。

这需要我们对系统的动态特性有深刻的理解，能够准确地把握系统的特点和参数。

只有这样，我们才能够有效地将系统的传递函数转化为能控标准型，为控制系统的设计和调节提供有力的支持。

在实际工程中，能控标准型的应用非常广泛。

比如在飞行器、汽车、机械设备等控制系统中，能控标准型都有着重要的应用价值。

通过对系统的传递函数进行分析和调节，我们可以使系统具有更好的控制性能和稳定性，从而提高系统的工作效率和安全性。

总之，传递函数能控标准型是控制系统理论中的重要概念，它对于系统的分析和设计具有重要的意义。

通过对传递函数进行变换和调节，我们可以将系统的动态特性清晰地呈现出来，为控制系统的设计和调节提供有力的支持。

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。

(1)写出系统状态空间表达式；(2)试设计一个状态反馈矩阵，将闭环极点特征值配置在j 53±-上。

)(t y题3-5-1图【解】：方法一：根据系统结构直接设状态变量如题3-5-1图所示，写状态空间表达式：[]x y u x x 10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--= 23111=⎥⎦⎤⎢⎣⎡--=c c U rank U系统能控，可以设计状态反馈阵。

设状态反馈阵为][21k k K = 状态反馈控制规律为：Kx r u -= 求希望特征多项式：34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式：)22()3()(1212k s k k s bK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵：]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k 方法二：[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A A A f U K c方法三：（若不考虑原受控对象的结构，仅从配置极点位置的角度出发）求系统传递函数写出能控标准型：2321)111()()(2++-=+-+=s s ss s s U s Y []xy u x x 10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= 求系统希望特征多项式：34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~：[][][]33236234~21=--==k k K [][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab bP⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P []1316~==P K K依据系统传递函数写出能控标准型ss s s s s s U s Y 2310)2)(1(10)()(23++=++= []x y u x x 0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式：464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵：[][][]144342604321=---==k k k K 。

第三章 线性控制系统的能控性和能观性3-3-1 判断下列系统的状态能控性。

（1）⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=01,0101B A （2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=111001,342100010B A （3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A （4）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1110,0000000011111B A λλλλ 【解】：(1)[]2,1011==⎥⎦⎤⎢⎣⎡-==n rankU AB BU c c ，所以系统完全能控。

(2)[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==7111111010012B A ABBU c 前三列已经可使3==n rankU c ，所以系统完全能控（后续列元素不必计算）。

（3）A 为约旦标准型，且第一个约旦块对应的B 阵最后一行元素全为零，所以系统不完全能控。

（4）A 阵为约旦标准型的特殊结构特征，所以不能用常规标准型的判别方法判系统的能控性。

同一特征值对应着多个约旦块，只要是单输入系统，一定是不完全能控的。

可以求一下能控判别阵。

[]2,111321031211312113121121132=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡==c c rankU B A BA AB BU λλλλλλλλλλλ，所以系统不完全能控。

3-3-2 判断下列系统的输出能控性。

(1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=xy u x x 011101020011100030013 (2) []⎪⎪⎩⎪⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x y u x x 0011006116100010【解】： （1）已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=020011,100030013B A ，⎥⎦⎤⎢⎣⎡-=011101C ，⎥⎦⎤⎢⎣⎡=0000D []⎥⎦⎤⎢⎣⎡--=111300002B CA CAB CB D前两列已经使[]22==m B CA CAB CB D rank ，所以系统输出能控。

绪论为了帮助大家在期末复习中能更全面地掌握书中知识点，并且在以后参加考研考博考试直到工作中，为大家提供一个理论参考依据，我们11级自动化二班的同学们在王整风教授的带领下合力编写了这本《现代控制理论习题集》（刘豹第三版），希望大家好好利用这本辅助工具。

根据老师要求，本次任务分组化，责任到个人。

我们班整体分为五大组，每组负责整理一章习题，每个人的任务由组长具体分配，一个人大概分1~2道题，每个人任务虽然不算多，但也给同学们提出了要求：1.写清题号，抄题，画图（用CAD或word画）。

2.题解详略得当，老师要求的步骤必须写上。

3.遇到一题多解，要尽量写出多种方法。

本习题集贯穿全书，为大家展示了控制理论的基础、性质和控制一个动态系统的四个基本步骤，即建模、系统辨识、信号处理、综合控制输入。

我们紧贴原课本，强调运用统一、联系的方法分析处理每一道题，将各章节的知识点都有机地整合在一起，力争做到了对控制理论概念阐述明确，给每道题的解析赋予了较强的物理概念及工程背景。

在课后题中出现的本章节重难点部分，我们加上了必要的文字和图例说明，让读者感觉每一题都思路清晰，简单明了，由于我们给习题配以多种解法，更有助于发散大家的思维，做到举一反三！这本书是由11级自动化二班《现代控制理论》授课老师王整风教授全程监管，魏琳琳同学负责分组和发布任务书，由五个小组组组长李卓钰、程俊辉、林玉松、王亚楠、张宝峰负责自己章节的初步审核，然后汇总到胡玉皓同学那里，并由他做最后的总审核工作，绪论是段培龙同学和付博同学共同编写的。

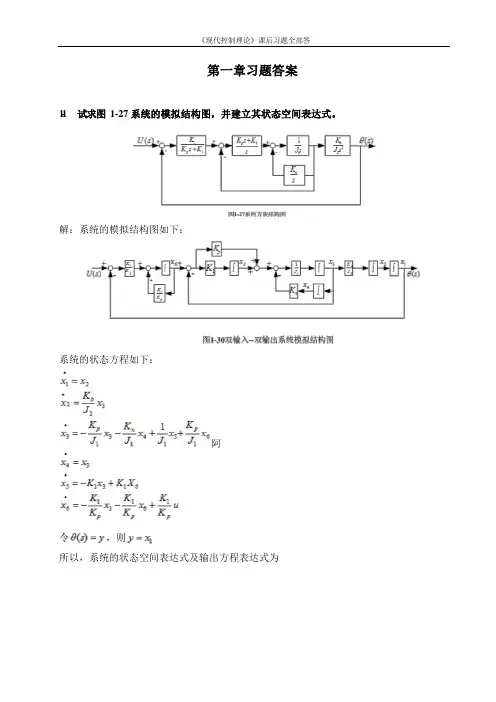
本书耗时两周，在同学的共同努力下完成，是二班大家庭里又一份智慧和努力的结晶，望大家能够合理使用，如发现错误请及时通知，欢迎大家的批评指正！2014年6月2日第一章 控制系统的状态空间表达式1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式 解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

传递函数的能控和能观测标准型实现方法王春侠【摘要】传递函数的实现问题是现代控制理论的重要课题之一.本文介绍了传递函数能控标准型和能观测标准型实现的两种方法,它们是基于微分方程的时域法和梅森公式的状态结构图法.结合能控标准型和能观测标准型的标准Ⅰ型和标准Ⅱ型实现,详细说明了这两种方法的应用.且展示了状态结构图法的便捷之处.【期刊名称】《电气电子教学学报》【年(卷),期】2018(040)001【总页数】4页(P112-115)【关键词】状态空间表达式;标准型;梅森公式;状态结构图【作者】王春侠【作者单位】陕西理工大学电气工程学院,陕西汉中 723001【正文语种】中文【中图分类】TP130 引言单输入单输出线性定常连续n阶系统微分方程的一般形式为(1)相应的传递函数为(2)由式(1)或者式(2)建立如下式(3)的状态空间表达式，称为系统的实现问题。

(3)为了分析和设计方便，通常规定状态空间表达式有能控标准型(标准Ⅰ型和标准Ⅱ型)、能观测标准型(标准Ⅰ型和标准Ⅱ型)和约当标准型这三类标准型式。

许多教科书介绍了能控标准Ⅰ型和Ⅱ型、能观测标准型Ⅰ型和Ⅱ型等四种实现，但大部分教科书对于这四种实现的状态变量如何选取未做出比较全面、简洁的解释，这给读者理解与学习这四种实现带来了一定的困难[1-5]。

本文给出由传递函数或者高阶微分方程建立能控标准型和能观测标准型的两种方法，即基于微分方程的时域法和基于梅森公式的状态结构图法。

下面以三阶系统为例，详细介绍这两种方法，其结论可以推广到n阶系统。

三阶系统微分方程的一般形式为(4)相应的传递函数为(5)其中β2=b2-a2b3β1=b1-a1b3β0=b0-a0b31 时域法1.1 能控标准Ⅰ型实现对式(5)，引入中间变量q，令(6)式(5)变形为(7)式(6)进行拉氏反变换得(8)对式(8)，选择状态变量x1=q(9)(10)(11)由式(9)～(11)、式(8)和式(7)，得能控标准Ⅰ型为y=β0 β1 β2X+b3u(12)1.2 能观测标准Ⅰ型实现对式(4)，选择状态变量x1=y-k3u(13)(14)(15)由式(13)～(15)，得(16)(17)并令(18)由式(16)～(18)和式(13)，得能观测标准Ⅰ型为y=1 0 0X+k3u(19)其中k3=b3k1=b1-a1k3-a2k3k0=b0-a0k3-a1k2-a2k11.3 能控标准Ⅱ型实现对式(8)，选择状态变量x3=q(20)(21)(22)由式(20)～(22)和式(8)，得(23)(24)(25)由式(23)～(25)和式(7)，得能控标准Ⅱ型为y=k2 k1 k0X+b3u(26)其中k2=β2k0=β0-a1k2-a2k11.4 能观测标准Ⅱ型实现对式(5)，引入中间变量z，令(27)式(5)变形为y=b3u+z(28)式(27)进行拉氏反变换得(29)对式(29)，选择状态变量x3=z(30)(31)(32)由式(30)～(32)和式(29)，得(33)(34)(35)由式(33)～(35)和式(28)，得能观测标准Ⅱ型为y=0 0 1X+b3u(36)由式(12)、式(19)、式(26)和式(36)可见，标准Ⅰ型的系统矩阵是底伴随矩阵，标准Ⅱ型的系统矩阵是右伴随矩阵。

《现代控制理论》第一章习题解答1.1线性定常系统和线性时变系统的区别何在？答：线性系统的状态空间模型为：x = AxBu+y CxDu= +线性定常系统和线性时变系统的区别在于：对于线性定常系统，上述状态空间模型中的系数矩阵A，B，C和中的各分量均为常数，而对线性时变系统，其系数矩阵D A，B，C和D中有时变的元素。

线性定常系统在物理上代表结构和参数都不随时间变化的一类系统，而线性时变系统的参数则随时间的变化而变化。

1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别？答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪几种标准形式？它们分别具有什么特点？答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。

对于n 阶传递函数G s( )= b s n−s1nn+−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0+d ，分别有⎧⎡0 1 0 0 ⎤⎡⎤0⎪⎢0 0 1 0 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎪x =⎢ ⎥x+⎢⎥ u ⑴能控标准型：⎨⎢0 0 0 1 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎣⎢−a0 −a1 −a2 −a n−1⎥⎦⎢⎥⎣⎦1⎪⎪⎩y=[b0 b1 b n−2 b n−1]x du+⎧⎡0 0 0 −a0 ⎤⎡b0 ⎤⎪⎪⎢⎢1 0 0 −a1 ⎥⎥⎢⎢b1 ⎥⎥⎪⎪x =⎢0 1 0 −a2 ⎥⎥x+⎢⎢ ⎥⎥u⑵能观标准型：⎨⎢b n−2⎥⎪⎢ ⎥⎢⎪⎣⎢0 0 1 −a n−1⎦⎥⎢⎣b n−1⎥⎦⎪⎪⎩y=[0 0 0 1]x du+⎧⎡p1⎪⎢0⎪x =⎢⎢ 0 p20 0 ⎤⎡1⎤0 ⎥⎢1⎥⎥x+⎢⎥u ⎥⎢ ⎥⎪⑶对角线标准型：⎨⎪⎢⎣0⎪p n⎥⎦⎢⎣1⎥⎦⎪⎩y=[c1 c2 c x du n] + 式中的pp1, 2,, p n和c c1, 2,, c n可由下式给出，G s( )= b s n−s1nn−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0 + =d s p−c1 1 + s p−c2 2 + + s p−c n n +d+能控标准型的特点：状态矩阵的最后一行由传递函数的分母多项式系数确定，其余部分具有特定结构，输出矩阵依赖于分子多项式系数，输入矩阵中的元素除了最后一个元素是1 外，其余全为0。