2009年全国初中数学联赛

2017年全国初中数学联赛决赛试卷B(3 月26 日上午8:45—11:15 )一、选择题(本题满分42分，每小题7分)本题共有6小题，每题均给出了代号为A、B、C、D的四个答案，其中有且仅有一个是正确的。

将你选择的答案的代号填在题号的括号内，每小题选对得7分；不选、错选或选出的代号字母超过一个(不论是否写在括号内) ，一律得0分。

1、若q是质数，且q +1是完全平方数，就称q为P型质数，则P型质数的个数是( )A、0B、1C、2D、无数个k .2、已知k为正实数，一次函数y=kx+1与反比例函数y=-的图象交于A(X1, y"，B(x2，Xy2)两点，若|X1-X2|= ,5,则k的值是( )A、1B、2C、,3D、2EF 53、已知AD、BE、CF为锐角△ ABC三边上的高，若AB=26，BC =后，贝V BE的长度是( )A、10B、12C、13D、244、在梯形ABCD 中，AB// CD，/ ABC=90° E是腰AD 的中点，若EC= 锁,AB+BC+CD=2 .''26,贝打BCE=( )A、30°B、45°C、60°D、75°5、若实数k使得关于x的方程(x2-)(kx2-x -8)=0恰有三个不同的实数根，则称k为“好数”，则“好数” k的个数是(C、36、记正整数m的各位数字之和为S(m)，比如S(2017)=2+0+1+7=10，现从1 , 2 ,3,…,2016,2017这2017个正整数中，任意取出n个不同的数，都能在这n个数中找到a i, a2，…，a7，a8,使得S(a" = S(a2)= •••= S(a7)= S(a8)，则正整数n的最小值是( )A、185B、187C、189D、191二、填空题(本大题满分28分，每小题7分)本题共有4小题，要求直接将答案写在横线上•—-2—x 1 17、若x^/3 42,则-X q-宁(|X|+1 + 帝)的值是 __________________8、在平面直角坐标系中，点O (0, 0)、A (0, 6)、B (-3, 2)、C (-2, 9),点P为线段OA (含端点)上任意一点，贝V PB+PC的最小值是______________9、有4只杯口全朝上的茶杯，现在每次翻转3只，翻动的茶杯允许再翻，经过n次翻动后，使得杯口全朝下，则正整数n的最小值是 _________(注：所谓一只茶杯的一次翻转是指将该茶杯的杯口朝上(下)翻为杯口朝下(上) ) 10、设A、B为抛物线y= x2上两点，该两点在y轴两侧，满足AB=4,记厶AOB的面积为S,其中O为坐标原点，则S的最大值是__________________三、解答题(本题满分20分)11、设a、b、c是任意三个互不相等的有理数，证明：匕+ 匕+ & 是(a -b) (b -c) (c -a)有理数•四、解答题（本题满分25分）12、如图，正方形ABCD绕A点逆时针旋转到正方形APQR,连接CQ,延长BP交CQ 于点E.⑴求证：E是线段CQ的中点;Bp⑵若CP丄BE,求PE的比值•A五、解答题（本题满分25分）13、如图，以直角厶ABC（其中/ C=90°的三边CA、CB、AB向外分别作正方形CADE、BCFG、ABHI，记边CB、CA的长分别为a、b;凸六边形DEFGHI的面积为S.问:是否在正整数a、b使得S=2016?若存在，请求出所有的正整数a、b,若不存在，请说明理由I H2017年全国初中数学联介竞赛试题参考答案及评分标准说明*评何试卷时.请依撫4•评兮标准•邊斤題和填空旳只设7分wo分两档* trnn. 请严格按科本评分标准规定的评分档次给分•不要再增加其他中间档次.如果考生的解齐力法如衣解答不同•只隻思路合理•步驟正确.圧评栓时请够照本评分标准划分的档次•给十相应的分数・一.选挣18（本邑満分42分.毎小E 7分）L B 2. A 3. D 4. B 5. D 6. A二.填空赳（本逍満分28分.毎小超7分）7、£8、5 + VTJ 9、4 10、8三.解答題（本題満分20分）1K站恥足任倉三个邸相^有理飲・呦,仙需占足自理故.tfWh 令x = • Wx)c#0- II丄 + 丄 + 丄=0. «5 分》x y 2十是少+忙♦二x=0・（10分）从而------ + -------- + ------- r(a-by (b_e)・ (e-a) *=x•+ ＞厂+二・=(x + y + :)2 - 2(xy + 齐♦ h) = (x + y +二)：.（15分）=—+-— * —-—是h 理数. a — b b_c c^a（20分）2017勺乞国杓陀説堂0・诀・・&$*及评分加応＜M 1 ill R 3 ii）12. talM. iF方彫•仏O绕・4 .占•迪时忡険转到iF方形.iPQR. mtCQ.址长BP交C0 于点£・（I）求if$ 段CQ的中点$（2）杵CP一BE.求需的比值.<1）谨结才C. AQ. AE. 正方形.IBCD^A^时什険转列正方形APQR.AC^AQ.厶B心ZG4Q・所以^BAP^^CAQ.所以乙IBP-厶4C0 （5分）li|）Z.15£^ ^ACE.所以儿B、C\三四点妹:乌・所以二<£OiUO180°・即冇*£丄（70 又因为AC^AQ.所以E是枚段CQ的中恵. （10分）<2）iZl:由<1〉A. B. C、E 四点共M可如.ZC£P-ZC£fl=ZC^=45% 所以PE"C・（15分）从而C£ = V2P£・（20分）故4匹=密=樂BP BP BP（25分》法2：由（1） J. B. C.£四点共卯可知.ZC£P^ZC£2UZC45=450.出以MJC. IRfiP 中4 " l AM.WJtli AB^iP. «rw^M 丄BP.由ZAMB M BPCM.（15 分）"BMM-ZPBC口ZPCB. AB二BC・所以所以MB^PC.BP 2BM7E"~PC Q0分）〈25 分）13. ttltL其中ZC ・9(T)的三边C. CB.川刃向外分别作正方形CADE. BCFG 、ABH1.记边CB ・Q 的长分别为a. 6：凸兀边形DEFGHI 的曲 枳为S.何，是否存任正矗救a. b.便得S = 2016?若〃任.请求出所升的正整故a. bi 若不«•讷说明理由•解：如用.延长必至厅・便BA -= AB . ii7C.则峪址 VCmMQ.从而= S^4C = S xac «5 分〉 同理* S 乂b =E M »C = S t y aG・则S ■ 4x£ab + 2(a'+F)・ 2(a‘ +b‘ 4ab)・■ f?设存任正廉tSd.b.便得S«=2016・即 瑚+b' + ab) = 2016・ 于^a 2^b\ab^24x32x7 •②由2 a'+ab + X 知a 上均为«tt <fia.b 均为奇救或A a.b -奇一偶.都宵a^ab+b 2为奇数.矛压人令a = "4% 代入®»0；+代+叭・2‘肿x7・类fcl 可知“4均为偶散.令a x « lx.b = ly •从而F+)'・xy ・3‘x7 3>( 15分)不妨设x^y. W32X 7^3X \ 故x 2£ll.注®^x.y 为正Cft.则x = 1.23.4. 当x = lH ・有y 】 + y = 62・即(2y+l)' = 249・ 柚 与 *・2 时.iiy 2^2y59. «P(v^l)2 » 60.当y = 3时.*3y = 54.解御)=6或y = -9 (舍去h 当 X = 4H< <J /-^4y = 47.即(>“2尸=51・因此满足③的if ¥ tt.r.j •只<ix»3. y«6或打x ■ 6.y ■ 3・①(10分)(20分》。

第一单元测试卷1一、填一填（21分，第4小题共5分，其余每空1分）（1）两个因数相乘的积是27.5，如果一个因数扩大10倍，另一个因数扩大10倍，积就扩大（），结果是（）。

（2）0.9+0.9+0.9+0.9改用乘法算式表示是（）。

（3）49×0.2积是（）位小数，0.35×0.7积是（）位小数，0.45×1.02积是（）位小数，150×7.4积是（）位小数。

（4）在○里填上“>”“<”或“=”（5分）6.7×0.98○6.7 6.09×1.3○6.09 3.9×1○1 6.3×2.04○2.04 18×0.35○0.354.8×7.5○7.5×4.8 56×0.86○56 87×1.15○87 1×0.98○1 8.25×1.1○8.25（5）0.23×0.8=( ),得数保留两位小数约是（）。

（6）一个长方形花坛，长是4.5米，宽是0.25米，它的面积是（）平方米。

（7）一书包的售价是48.5元，买2个要付（）元，买4个要付（）元。

（8）3.56×3+7×3.56可以用（）律进行简算，0.25×9.5×8可以用（）律进行简算。

（9）一匹马的时速约为62千米,一只猎豹的速度是马的1.4倍,猎豹的时速约为( )千米。

（10）把6.73改写成与它大小相等的三位小数是（）。

二、判一判（5分）（1）一个数乘小于1的数, 积比原数小。

（）（2）7.2×0.78 > 7.2 ( )（3）8.9995用“四舍五入”法精确到百分位是9.00。

( )（4）3.03×2.06的积有四位小数。

（）（5）一个数乘100，等于将这个数扩大到它的100倍。

（）三、选一选（5分）。

（1）18.491保留两位小数的近似值是（）A、18.49 B、18.5 C、18.50（2）下面的算式中，积等于100的是（）A、2.5×400 B 、24×5 C、125×0.8（3）近似值13.2是把一个小数保留一位小数时所得到的，下列各数中（）不可能是这个小数。

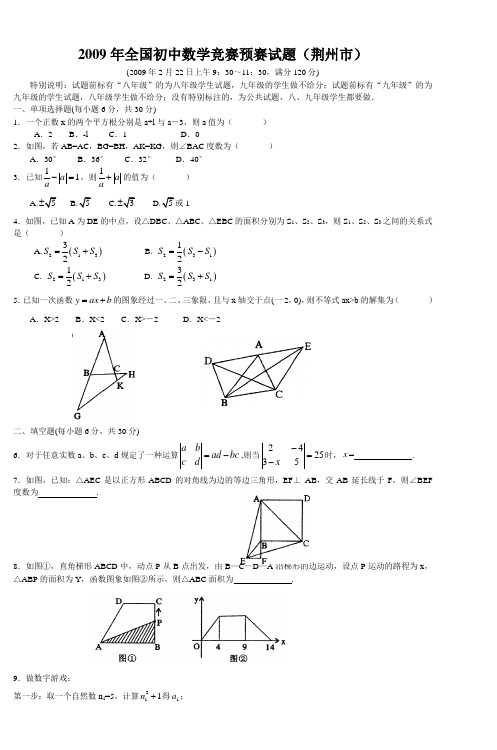
2009年全国初中数学竞赛预赛试题（荆州市）(2009年2月22日上午9：30～11：30，满分120分)特别说明：试题前标有“八年级”的为八年级学生试题，九年级的学生做不给分；试题前标有“九年级”的为九年级的学生试题，八年级学生做不给分；没有特别标注的，为公共试题，八、九年级学生都要做．一、单项选择题(每小题6分，共30分)1．一个正数x 的两个平方根分别是a+l 与a －3，则a 值为（ ）A ．2B ．-lC ．1D ．02．如图，若AB=AC ，BG=BH ，AK=KG ，则∠BAC 度数为（ ）A ．30°B ．36°C ．32°D ．40°3．已知11a a -=，则1a a+的值为（ ）A. C. 14．如图，已知A 为DE 的中点，设△DBC 、△ABC 、△EBC 的面积分别为S 1、S 2、S 3，则S 1、S 2、S 3之间的关系式是（ ） A.()21332S S S =+ B. ()23112S S S =- C. ()21312S S S =+ D. ()23132S S S =+ 5．已知一次函数y ax b =+的图象经过一、二、三象限，且与x 轴交于点(一2，0)，则不等式ax>b 的解集为（ ）A ．X>2B ．X<2C ．X>－2D ．X<－2二、填空题(每小题6分，共30分)6．对于任意实数a 、b 、c 、d 规定了一种运算a bad bc c d =-,则当242535x -=-时，x =______________. 7．如图，已知：△AEC 是以正方形ABCD 的对角线为边的等边三角形，EF ⊥ AB ，交AB 延长线于F ，则∠BEF 度数为______________.8．如图①，直角梯形ABCD 中，动点P 从B 点出发，由B —C —D —A 沿梯形的边运动，设点P 运动的路程为x ，△ABP 的面积为Y ，函数图象如图②所示，则△ABC 面积为______________.9．做数字游戏：第一步：取一个自然数n 1=5，计算211n +得1a ；第二步：算出1a 的各位数字之和得n 2，计算221n +得2a ；第三步：算出2a 的各位数字之和得n 3，计算231n +得3a ；……依此类推，则2009a =______________.10．(八年级)已知关于X 的方程a(x －3)+b(3x+1)=5(x+1)有无穷多个解，则a+b=______________.(九年级)已知方程210x mx m +-+= (m 是整数)有两个不等的正整数根，则m=______.三、解答题(本大题共4小题，每小题15分，共60分)11．在底面积为l00cm 2、高为20cm 的长方体水槽内放人一个圆柱形烧杯(烧杯本身的质量、体积忽略不计)．如图所示．向烧杯中注入流量一定．．．．的水．注满烧杯后。

一级建造师《机电工程管理与实务》模拟试题（一）(考试时间4小时，满分160分)一、单项选择题(每题1分。

每题的备选项中，只有1个最符合题意)1．对开环控制系统按给定控制方式特点的表述中，下列错误的是（）。

A．控制的精度准确性较差B．控制原理简单C．控制作用的传递具有多向性D．因为结构简单、调整方便、成本低，应用面很广2．（）主要用于在机械运转中随时将主、从动轴结合或分离。

A．联轴器B．联轴器和离合器C．离合器D．自动离合器3．键主要用来实现轴和轴上零件之间的周向固定以传递( )。

A、弯矩B、扭矩C、力D、速度4．高压隔离开关作用主要是( )。

A、隔离高压电源，保证安全检修B、分断电路中的用电负荷C、保护电路中的用电设备D、分断大电流电路5．下列对工业纯铜的描述错误的是（）。

A．密度为8.969／cm3B．具有良好的导电性C．导热性差D．具有优良的焊接性能6．在电阻电路、电感电路、电容电路中，电流和电压关系的共同点是（）。

A．电流与电压同频率B．电压相位超前电流相位90°C．电压与电流同相位D．电流相位超前电压相位90°7．自动控制系统主要的特点是有反馈存在，按()进行控制。

A、偏差B、电压C、电流D、给定值8．基孔制的孔为基准孔，基准孔的代号为（）。

A．B B．HC．b D．h9．轴的材料通常采用（）。

A．合金钢和普通钢B．普通钢的冷拉钢C．碳素钢和普通钢D．碳素钢和合金钢10．轴承的功用是为支承轴及轴上零件，承受其荷载，并保持轴的旋转精度，减少轴与支承的摩擦和磨损。

通常轴承分为（）。

A．推力轴承和滑动轴承B．向心轴承和滚动轴承C．滑动轴承和滚动轴承D．推力轴承和向心轴承11．()是将电解液中的金属离子在直流电的作用下，在阴极上沉积出金属而形成镀层的工艺过程。

A、热镀B、渗镀C、电镀D、喷镀12．电动机的额定功率是指在额定电压、额定频率下满载运行时电动机( )。

A、输入的机械功率B、轴上输出的机械功率C、输入功率D、轴上输出的电功率13．在现场环境限制较多、其他起重机无法进行吊装的场合，且被吊设备或构件几何寸大、重量重的机电设备安装和大型结构安装工程中，首先考虑选用( )起重机。

关于公布2009年全国初中数学联赛获奖名单的通知各县（市）、区教育局教研室、市直属中学：4月12日举行了2009年全国初中数学联赛，在各县、市、区教研室及学校的大力支持下，已圆满结束。

现将团体优胜奖、学生一二三等奖及优秀指导教师奖予以公布，请校对。

附件1：2009年全国初中数学联赛团体优胜奖名单附件2：2009年全国初中数学联赛获奖名单附件3：2009年全国初中数学联赛优秀指导教师奖名单宁波市教育局教研室2009年4月23日附件1：2009年全国初中数学联赛团体优胜奖名单团体优胜奖（共7名）镇海区蛟川书院慈溪实验中学宁波外国语学校鄞州区田莘耕中学慈溪阳光实验学校鄞州宋诏桥中学鄞州古林镇中学附件2：2009年全国初中数学联赛获奖名单一等奖张馨怡镇海区蛟川书院干于越镇海区蛟川书院张挺鄞州区田莘耕中学钱旭楠鄞州区宋诏桥中学王宁鄞州区古林镇中学邵峰鄞州区李关弟中学曹旸慈溪实验中学陈栋慈溪实验中学高笑潇慈溪实验中学龚梦佳慈溪市新世纪实验学校王瑞瑆慈溪市观海卫初中房君锋慈溪实验中学蒋晓天慈溪育才中学陈哲晖慈溪阳光实验学校周正泽镇海区蛟川书院竺俊博镇海区蛟川书院陈佳云镇海区蛟川书院王聪镇海区蛟川书院崔爽怡镇海区蛟川书院吴思晗镇海区蛟川书院郑小东镇海区蛟川书院周笑天镇海区蛟川书院郑天海北仑顾国和外国语学校周琛宁波外国语学校胡九匀宁波外国语学校韩鑫宁波外国语学校王佳栋镇海区蛟川书院周逸云镇海区蛟川书院毛行健象山县文峰学校陈科彪鄞州区姜山实验中学袁淦慈溪实验中学徐旭程慈溪实验中学吴奇鲁北仑顾国和外国语学校张泽寰鄞州区宋诏桥中学毕腾锋鄞州区李关弟中学金焕鄞州区田莘耕中学崔丹杰鄞州区田莘耕中学周超男鄞州区古林镇中学毛佳乐鄞州区横街中学陈姣姣慈溪阳光实验学校任沛伦慈溪实验中学张成竹镇海区蛟川书院吕晨镇海区蛟川书院马梦琪镇海区蛟川书院董舒羽镇海区蛟川书院李瑞洲宁波华茂外国语学校杨陈昕镇海区蛟川书院谢李兴镇海区仁爱中学滕皓鄞州区宋诏桥中学耿皓鄞州区宋诏桥中学柴珏辉鄞州区宋诏桥中学余阳慈溪阳光实验学校周军杰慈溪育才中学王丰镇海区蛟川书院吴可凡宁波市明楼中学陈双乐宁波外国语学校严煜东慈溪市新世纪实验学校梁海浪鄞州区集士港中学朱煜宗鄞州区宋诏桥中学王铖慈溪市上林中学黄舒荟镇海区蛟川书院范勇镇海区蛟川书院周斐鄞州区姜山实验中学王家宁鄞州区古林镇中学吴雪松慈溪阳光实验学校岑益鹏慈溪育才中学俞雷钧宁波外国语学校陈哲泳宁波外国语学校杨旭雷鄞州区田莘耕中学孙强鄞州区田莘耕中学龚科铭鄞州区宋诏桥中学汪力晟鄞州区宋诏桥中学谢静含鄞州区宋诏桥中学毛凯杰鄞州区集士港中学胡航恺慈溪实验中学胡超元慈溪市新城中学李明慈溪实验中学岑晟慈溪实验中学何人可宁海跃龙中学吕宣融镇海区蛟川书院王一舟宁波外国语学校张光宇宁波外国语学校叶万达宁波外国语学校叶凯文宁波华茂外国语学校叶明翔镇海应行久外语实验学校成励翊慈溪阳光实验学校胡觅阳慈溪实验中学二等奖林繁荣鄞州区塘溪中学陈彬鄞州区姜山镇中心中学邬乐婷奉化实验中学周志毅宁海跃龙中学金焱波宁波东海实验学校张寒之宁波外国语学校夏立伟宁波外国语学校干文捷宁波外国语学校赵斌鄞州区田莘耕中学王荣晟宁波市东恩中学胡冯钦宁波外国语学校马宇桥宁海跃龙中学殷学杰鄞州区李关弟中学周易宁海潘天寿中学胡艇艇北仑芦江书院蒋哲宁波外国语学校王乐乐宁波外国语学校王逸璐宁波东海实验学校丁燕岚北仑芦江书院石强宁波市东恩中学沈汪莹鄞州区横街中学马浙平奉化城北中学吴鹏飞宁海城关中学尤小龙宁海跃龙中学方舟象山县文峰学校杨屹羚象山县文峰学校袁梦阳宁波东海实验学校楼昕烨北仑顾国和中学徐雨哲宁波外国语学校周柯琪宁波东海实验学校周馨奉化实验中学王启楠宁波东海实验学校冯迭乔宁海潘天寿中学胡丁冉象山丹城中学朱浩宁波惠贞书院江海奉化实验中学尤淑华宁海桃源中学金宇阳宁波七中姜仑宁波七中邱立本宁海跃龙中学王一雯象山县文峰学校竺金磊奉化城北中学王琛象山县文峰学校殷俊杰象山县文峰学校王俊恺象山县文峰学校王安琪顾国和外国语学校张捷宁波市东恩中学刘奇磊宁波市第十五中学徐晨宁波惠贞书院顾鹏真宁波市第十五中学吴朝阳宁波市明楼中学颜华卿宁波市东恩中学王挺奉化实验中学翁亦青宁波市第十五中学刘泽春宁波市东恩中学忻光耀宁波市第十五中学周汝栋宁波市第十五中学周啸霄宁波市曙光中学胡钦赢宁波七中孔津聿江北实验中学蓝旭丹奉化锦屏中学金协城宁海跃龙中学顾博超象山县文峰学校俞翰毅象山县荔港学校崔宁宁波市曙光中学陈昀臻奉化锦屏中学薛佳伟宁海跃龙中学黄建华宁海跃龙中学王艳玲象山滨海学校何立伟宁波市第十五中学许倩倩宁波市东恩中学周凡宁波市翠柏中学毛临风宁波七中翁哲伟宁波外国语学校葛腾辉宁海跃龙中学应海旭宁波市第十五中学李依纯象山县丹城中学房伟康宁波七中张雨鸣奉化奉港初中朱李栋奉化锦屏中学陈玮奉化锦屏中学应京含奉化锦屏中学娄学思宁海跃龙中学王洁科宁海长街镇中史丹丽象山县文峰学校周嘉懿象山县文峰学校竺琦玫象山县文峰学校吴珂璟宁波市东恩中学范佳乐宁波市东恩中学忻仕杰宁波市曙光中学李雯倩宁波惠贞书院周芸宁波市幸福苑实验学校朱旭律宁波惠贞书院莫伊娜奉化实验中学徐鑫奉化锦屏中学吴祚煜象山文峰学校李时天宁波惠贞书院乌帅宁波庄桥中学张意楠宁波七中陈正宇宁波惠贞书院唐晨宁波惠贞书院吴佳成宁波七中楼哲炜宁波惠贞书院陈旭东宁波七中陈欣源宁波惠贞书院罗靖茜宁波惠贞书院顾圣涛宁波惠贞书院周梦蝶宁波惠贞书院三等奖毛佩琦鄞州区集士港中学潘露微鄞州区田莘耕中学吴欣怡鄞州区宋诏桥中学虞炎彬鄞州区古林镇中学徐广渊鄞州区姜山实验中学蒋阳阳鄞州区集士港中学陈玲丹鄞州区古林镇中学胡柯立鄞州区横街中学徐慧鄞州区田莘耕中学章莎莎鄞州区宋诏桥中学黄焕鄞州区宋诏桥中学周卓超鄞州区古林镇中学任超敏鄞州区古林镇中学应瑜鄞州区樟村中学殷学杰鄞州区李关弟中学徐倩梦鄞州区田莘耕中学周秀秀鄞州区逸夫中学戴科泉鄞州区宋诏桥中学熊雪婷鄞州区宋诏桥中学蒋雨晴鄞州区宋诏桥中学潘俊杰鄞州区宋诏桥中学朗天楠鄞州区宋诏桥中学王政鄞州区集士港中学楼莹雯鄞州区古林镇中学任启盈鄞州区古林镇中学余黄伟鄞州区古林镇中学陈宇迪鄞州区集士港中学俞晓露鄞州区集士港中学高胜寒慈溪市实验中学孙蒙召慈溪市新城中学孙莉慈溪市阳光实验余树干慈溪市阳光实验毛梦丹慈溪市实验中学何伟栋慈溪市实验中学陈裕梁慈溪市锦纶中学徐金金慈溪市育才中学陈嘉瑜慈溪市阳光实验褚云峰慈溪市锦纶中学楼霆慈溪市巷城初中冯榆晨慈溪市逍林中学陈曦孛慈溪市实验中学邹云剑慈溪市新世纪沈启慈溪市实验中学孙一材慈溪市实验中学沈翔慈溪市实验中学张译慈溪市育才中学孙家乐奉化市实验中学张晟奉化市实验中学毛柔燕奉化市实验中学傅丽琴宁波东方外国语学校林泼奉化市锦屏中学陈攀绩奉化市锦屏中学余路炜奉化市实验中学周函婷奉化市城北中学单许桓奉化市城北中学徐飞奉化市奉港初中胡悠宁波求真学校邬炳科奉化市西坞中学肖浩泉奉化市莼湖初中李夏蔚奉化市实验中学周经纬奉化市实验中学任珂朴宁海跃龙中学徐海松宁海桃源中学应俊宁海跃龙中学潘俊飞宁海跃龙中学江伊丽宁海跃龙中学葛先科宁海桃源中学徐如媚宁海桃源中学陈纤予宁海桃源中学崔露允宁海西店中学葛为宗宁海跃龙中学陈田甜宁海桃源中学赵坚宁海跃龙中学范嘉帆宁海潘天寿中学葛东波宁海潘天寿中学何贤武宁海城关中学胡锦浩宁海西店中学葛素素象山县文峰学校鲍文焕象山县文峰学校徐嘉楠象山县文峰学校章牧遥象山县文峰学校王翰江象山县文峰学校鲍舒云象山县文峰学校赖一鸣象山县滨海学校钱栩象山县丹城二中杨莎莎象山县滨海学校王启帆象山县文峰学校余晨沁象山县文峰学校陈波象山县新港中学王蓓佳象山县滨海学校吕蜂象山县新港中学陈瑜超象山县文峰学校沈应豪象山县文峰学校周璐象山县文峰学校范中杰镇海区蛟川书院顾天长镇海区蛟川书院李哲燏镇海区蛟川书院王竹升镇海区蛟川书院陈凯琦镇海区蛟川书院顾全镇海区蛟川书院仇明月镇海区蛟川书院刘嘉威镇海区仁爱中学金辉镇海区蛟川书院胡金杰镇海区蛟川书院施信超镇海区蛟川书院周天漪镇海区蛟川书院徐文凯镇海区蛟川书院章维明镇海区蛟川书院范天奇镇海区蛟川书院刘媛镇海区蛟川书院翁文涛镇海区蛟川书院蔡哲宁镇海区蛟川书院张学磊镇海区蛟川书院翁凯浩镇海区蛟川书院王铮镇海区蛟川书院张易凡镇海区蛟川书院袁鑫北仑区顾国和外国语学校方鑫磊北仑区东海实验董浩凯北仑区芦江书院宋晶晶北仑区东海实验吴卓辉北仑区东海实验虞小英北仑区顾国和外国语学校张丹维北仑区东海实验王钢杰北仑区松花江中学沈麒北仑区东海实验毛一帆北仑区东海实验冯璐北仑区顾国和外国语学校赵宇翔北仑区顾国和外国语学校吴松展北仑区东海实验乐可辛北仑区长江中学陈鑫北仑区江南中学奚洋洋北仑区联合实验中学黄鹤鸣宁波市东恩中学毛天慧宁波市第十五中学杨默宁波市第十五中学张仁杰宁波市东恩中学梅奕欣宁波市第十五中学黄杰宁波市第十五中学陈晔宁波市第十五中学石俊宁波市李兴贵中学朱家琰宁波市东恩中学吴海宁波市东恩中学马淑君宁波市第十五中学张一诺宁波市第十五中学杨峥宁波市第十五中学陈勇道宁波市翠柏中学王慧质宁波市第十五中学史笛宁波市第十五中学项溥原宁波市李兴贵中学徐嘉烨宁波市东恩中学孙怡然宁波七中孙卓宁波七中王欣轶宁波市第十九中学钟逸霏宁波市曙光中学施哲朴宁波七中金俊琦宁波七中陈冠宇宁波七中陈盛臻宁波七中罗吉君宁波市春晓中学徐俊杰宁波七中朱怡宁波市幸福苑实验学校吴悦旻宁波市曙光中学张文嵩宁波七中杨展宁波七中薛嵩宁波市曙光中学洪磊宁波市洪塘中学陈瑜宁波市惠贞书院王亦君宁波市慈湖书院唐亚正宁波市洪塘中学张文杰宁波市修人学校郑佳浩宁波市洪塘中学陈思澹宁波市惠贞书院马夏冰宁波市实验中学方磊宁波市妙山学校任凯宁波市妙山学校汤雨欣宁波市惠贞书院王梁坤宁波市惠贞书院梁善林宁波市洪塘中学戴妍妍宁波市惠贞书院汪儒灏宁波市三江中学郑思超宁波市三江中学源逸宁波市惠贞书院胡玄烨宁波兴宁中学王梦阳宁波外国语学校伍天禾宁波外国语学校杨汐宁波万里学校李乾宁波外国语学校严喆宁波华茂外国语学校王品安宁波万里学校罗玥琦宁波兴宁中学徐天忆宁波外国语学校任佳星宁波外国语学校熊天竹宁波外国语学校卓家隆宁波外国语学校刘震宁波外国语学校姚文婕宁波兴宁中学张文瑜宁波华茂外国语学校胡霄月宁波外国语学校周迪龙宁波外国语学校王虹宁波信懋学校附件3：2009年全国初中数学联赛优秀指导教师奖名单鄞州区袁君吴亚红王可芳华亚君戴华君张勇陈军张亚波慈溪市华漫天陈雪峰戴萍袁浩杰曹太星郑建忠王震曹太星陈国文叶建丰陈海波邹波奉化市谢寒竺孟辉何春芳邬世芬殷志存郑小玉俞武彬王亚芬王琳宁海县林红年胡亚云金齐斌杨芬仙陈建华林红年陈黎丽胡建勋周银芬国漫春鲍丽娜祁春琴李华蒋景贤胡余建象山县孙兴法王萍韩苏文方德懿朱炜炜王如启韩海亚镇海区刘清泉邓俊徐其学縢丽陈琦余维俭北仑区阮肖锋洪永忠陈孝凯邹微微王建垂张洪波丁燕波洪永忠周志程海曙区朱斌康潘菁菁徐平平顾信华董景荣邬珊珊冯玲青顾美琴徐淑贞江东区厉红信陕全录樊贞慧章剑雄杜斌蒋晓琳包伊娜张幼云卓晓敏孟笑宇梁卫东江北区直属鲍雨红郑瑄潘红波孙碧嫣卢芳芳胡翔鲁玲莉洪利芳周伟蔚方岩。

历年(95-10)年全国数学竞赛(联赛)分类题型详解 - 几何(1)选择题(30道题)1. 如果边长顺次为25、39、52与60的四边形内接于一圆，那么此圆的周长为［ ]A．62πB．63π C．64πD．65π1995年全国初中数学联赛试题答案: D详解：四个选择支表明，圆的周长存在且唯一，从而直径也存在且唯一．又由AB2＋AD2 ＝252＋602 ＝52×（52＋122）＝52×132＝(32＋42)×132 ＝392＋522 ＝BC2＋CD2故可取BD＝65为直径，得周长为65π，选D．2. 设AB是⊙O的一条弦，CD是⊙O的直径，且与弦AB相交，记M＝｜S△CAB－S△DAB｜，N＝2S△OAB，则[ ]A．M＞N B．M＝N C．M＜N D．M、N的大小关系不确定1995年全国初中数学联赛试题答案: B详解1: 不失一般性，设CE≥ED，在CE上取CF＝ED，则有OF＝OE，且S△ACE－S△ADE＝S△AEF＝2S△AOE．同理，S△BCE－S△BDE＝2S△BOE．相加，得S△ABC－S△DAB＝2S△OAB，即M＝N．选B．详解2: 若过C、D、O分别作AB的垂线（图3），CE⊥AB、DF⊥AB、OL⊥AB，垂足分别为E、F、L．连CF、DE，可得梯形CEDF．又由垂径分弦定理，知L是EF的中点．根据课本上做过的一道作业：梯形对角线中点的连线平行底边，并且等于两底差的一半，有｜CE－DF｜＝2OL．即M＝N．选B．3．如图，A是半径为1的圆O外的一点，OA=2，AB是圆O的切线，B是切点，弦BC∥OA，连结AC，则阴影部分的面积等于[ ]1996年全国初中数学联赛试题答案: B4．如果一个三角形的面积和周长都被一直线所平分，那么该直线必通过这个三角形的[ ]A．内心B．外心C．重心D．垂心1996年全国初中数学联赛试题答案: A5．如果20个点将某圆周20等分，那么顶点只能在这20个点中选取的正多边形的个数有[ ]A．4个B．8个 C．12个 D．24个1996年全国初中数学联赛试题答案: C6. 在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积等于（）（Ａ）12（Ｂ）14（Ｃ）16（Ｄ）181998年全国数学联赛试卷答案: C详解: 连ED，则又因为DE是△ABC两边中点连线，所以故选C．7．一个凸n边形的内角和小于1999°，那么n的最大值是（）．A．11 B．12 C．13 D．141999年全国初中数学竞赛答案: C8．在三角形ABC 中，D 是边BC 上的一点，已知AC=5，AD=6，BD=10，CD=5，那么三角形ABC 的面积是（ ）．A ．30B ．36C ．72D ．1251999年全国初中数学竞赛答案: B9．在正五边形ABCDE 所在的平面内能找到点P ，使得△PCD 与△BCD 的面积相等，并且△ABP 为等腰三角形，这样的不同的点P 的个数为（ ）．A ．2B ．3C ．4D ．51999年全国初中数学竞赛答案: D10. 设a ，b ，c 分别是△ABC 的三边的长，且cb a b a b a +++=，则它的内角∠A 、∠B 的关系是（ ）。

12009年全国初中数学联合竞赛试题参考答案第一试一、选择题（本题满分42分，每小题7分）1．设71a =，则32312612a a a +--=（ ）A ．24B ．25C ．4710D ．4712【解析】 A ．由()217a +=，有2226,62a a a a +==-．于是32312612a a a +--()()3621262612a a a a =-+---()2261212621224a a a a =+-=+-=2．在ABC △中，最大角A ∠是最小角C ∠的两倍，且7AB =，8AC =，则BC =（ ）A ．2B ．10C 105D ．73【解析】 C ．做A ∠的角平分线交BC 边于D ．于是78AB BD AC DC ==．不妨设7,8BD x DC x ==，由BAD BAC △∽△，有BD AB AB BC =，即77715x x =，于是715x ，15105BC x =3．用[]x 表示不大于x 的最大整数，则方程[]2230x x --=的解的个数为（ ）2A ．1B ．2C ．3D ．4【解析】 C ．原问题等价于函数23y x =-与函数[]2y x =的图像的交点个数问题．观察出交点个数为3个．方程的解分别为2,3x x =-=，另一个位于2，3之间．4．设正方形ABCD 的中点为点O ，在以五个数A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个，它们的面积相等的概率为（ ）A ．314B ．37C ．12D ．47【解析】 B ．不妨设三角形边长为1，则三角形的面积有两种，一种是14，形如ABO △，有4个；一种是12，形如ABD △，有4个．于是对于这8个三角形，先选出任意一个，再选出其余7个三角形中面积和它相等的三角形（共3个）中的一个，概率为37．5．如图，在矩形ABCD 中，3AB =，2BC =，以BC 为直径在矩形内作半圆， 自点A 作半圆的切线AE ，则sin CBE ∠=（ ）A 6B ．23C ．13D 103ECBDA【解析】 D ．取BC 中点F ，连接AF ，则CBE BAF ∠=∠，于是2210sin sin 13CBE BAF ∠=∠==+6．设n 是大于1909的正整数，使得19092009n n--为完全平方数的n 的个数是（ ）A ．3B ．4C ．5D ．6【解析】 B ．由1909100120092009n n n -=-+--，而1002009n-可能取整数2,5,4,10,25,50,100．若10012009n --为完全平方数，则有1002,5,10,502009n=-．于是这样的n 有4个．二、填空题（本题满分28分，每小题7分）1．已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，则()()2211a b --的最小值是 ．【解析】3-．2,1a b ab t +==-，又由0∆≥知2t 1≤≤．于是()()()222222111a b a b a b --=+-+424t =-．于是当1t =时代数式有最小值3-．2．设D 是ABC △ 的边AB 上的一点，作DE BC ∥交AC 于点E ，作DF AC ∥交BC 于点F ，已知ADE △、DBF △的面积分别为m 和n ，则四边形DECF 的面积为 ．【解析】 2mn ADE BDF △∽△，相似比为ADDB．观察到DEF △的面积等于m 和n 的等比中项，所以所求答案为2mn3．如果实数a ，b 满足条件221a b +=，221221a b a b a -+++=-，则a b += ．【解析】 1-．分情况讨论，可得221221a b a b a -+++=-或22(12)21a b a b a --+++=-．如果是第一种，则222b b a +=-，消去a 可得2230b b --=，可得1b =-或32．经检验，1,0b a =-=符合，所求结果为1-；如果是第二种，则224a b b a -=-．因为去绝对值符号的时候有120a b -+≤，即21a b +≥，而10b +≥，则设法凑出含有1b +的形式．因为2240a a b b +--=，所以2222114()22a ab b a b +--++=，即22238(1)4a a b a +=+≤，所以8a ≥或0a ≤，因此只能有0a =，和第一种情况是同一个解．4．已知a ，b 是正整数，且满足15152a b 是整数，则这样的有序数对()a b ，共有 对．5【解析】 7．显然两个根式的值都是有理数（否则把它平方即可发现）．穷举，可能是1+1，112+， 1122+，1144+，1136+，考虑顺序，共7种．第二试（A ）一、（本题满分20分）已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．⑴ 证明：P ⊙与y 轴的另一个交点为定点．⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值． 【解析】 ⑴ 易求得点C 的坐标为()0c ，， 设()10A x ，，()20B x ，，则12x x b +=-，12x x c =． 设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====． 因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上，旗开得胜6所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，， 即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△， 解得23b =±．二、（本题满分25分）设CD 是直角三角形ABC 的斜边AD 上的高，1I 、2I 分别是ADC △、BDC △的内心，3AC =，4BC =，求12I I ．I 2I 1CABBACE DFI 1I 2【解析】 作1I E AB ⊥于E ，2I F AB ⊥于F ．旗开得胜7在直角三角形ABC 中，3AC =，4BC =，225AB AC BC +=．又CD AB ⊥，由射影定理可得295AC AD AB ==， 故165BD AB AD =-=，22125CD AC AD -． 因为1I E 为直角三角形ACD 的内切圆的半径，所以()11325I E AD CD AC =+-=． 连接1DI 、2DI ，则1DI 、2DI 分别是ADC ∠和BDC ∠的平分线，所以112245I DC I DA I DC I DB ∠=∠=∠=∠=o，故1290I DI ∠=o，所以12I D I D ⊥，1113325sin sin 45I E DI ADI ===∠o ． 同量，可求得245I F =，242DI ． 所以2212122I I DI DI +三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②旗开得胜8a b c【解析】证法1：将①②两式相乘，得()8b c a c a b a b c a b c bcca ab +-+-+-⎛⎫++++= ⎪⎝⎭，即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦，即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c9证法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=， 变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦， 即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c第二试（B ）一、（本题满分20分）已知二次函数()20y x bx c c =++<的图象与x 轴的交点分别为A 、B ，与y 轴的交点为C ．设ABC △的外接圆的圆心为点P ．10⑴ 证明：P ⊙与y 轴的另一个交点为定点．⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值． 【解析】 ⑴ 易求得点C 的坐标为()0c ，， 设()10A x ，，()20B x ，，则12x x b +=-，12x x c =． 设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====． 因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上， 所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，， 即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△， 解得23b =±．旗开得胜11二、（本题满分25分）已知ABC △中，90ACB ∠=o ，AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F ．求证：DE AB ∥．ACBHNMF P EQQEP F MNHBCA【解析】 因为BN 是ABC ∠的平分线，所以ABN CBN ∠=∠．又因为CH AB ⊥，所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ，因此CQ NC =．又F 是QN 的中点，所以CF QN ⊥，所以90CFB CHB ∠==∠o ，因此C 、F 、H 、B 四点共圆．又FBH FBC ∠=∠，所以FC FH =，故点F 在CH 的中垂线上．、同理可证，点E 在CH 的中垂线上．旗开得胜12因此EF CH ⊥，又AB CH ⊥，所以EF AB ∥．三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】证法1：将①②两式相乘，得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭， 即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，13即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦，即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c证法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=， 变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦， 即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c第二试（C）一、（本题满分20分）△的已知二次函数()20y x bx c c=++<的图象与x轴的交点分别为A、B，与y轴的交点为C．设ABC 外接圆的圆心为点P．⊙与y轴的另一个交点为定点．⑴ 证明：P1415⑵ 如果AB 恰好为P ⊙的直径且2ABC S =△，求b 和c 的值． 【解析】 ⑴ 易求得点C 的坐标为()0c ，， 设()10A x ，，()20B x ，，则12x x b +=-，12x x c =． 设P ⊙与y 轴的另一个交点为D ，由于AB 、CD 是P ⊙的两条相交弦，它们的交点为点O ，所以OA OB OC OD ⨯=⨯则121x x c OA OB OD OC c c⨯====． 因为0c <，所以点C 在y 轴的负半轴上，从而点D 在y 轴的正半轴上， 所以点D 为定点，它的坐标为()01，． ⑵ 因为AB CD ⊥，如果AB 恰好为P ⊙的直径，则C 、D 关于点O 对称，所以点C 的坐标为()01-，， 即1c =-．又()()222121212444AB x x x x x x b c b =-+---+所以21141222ABC S AB OC b =⋅+⋅△， 解得23b =±．16二、（本题满分25分）已知ABC △中，90ACB ∠=o ，AB 边上的高线CH 与ABC △的两条内角平分线AM 、BN 分别交于P 、Q 两点PM 、QN 的中点分别为E 、F ．求证：DE AB ∥．ACBHNMF P EQQEP F MNHBCA【解析】 因为BN 是ABC ∠的平分线，所以ABN CBN ∠=∠．又因为CH AB ⊥，所以9090CQN BQH ABN CBN CNB ∠=∠=-∠=-∠=∠o o ，因此CQ NC =．又F 是QN 的中点，所以CF QN ⊥，所以90CFB CHB ∠==∠o ，因此C 、F 、H 、B 四点共圆．又FBH FBC ∠=∠，所以FC FH =，故点F 在CH 的中垂线上．、同理可证，点E 在CH 的中垂线上．因此EF CH ⊥，又AB CH ⊥，所以EF AB ∥．17三、（本题满分25分）已知a ，b ，c 为正数，满足如下两个条件：32a b c ++= ①14b c a c a b a b c bc ca ab +-+-+-++= ②a b c【解析】解法1：将①②两式相乘，得()8b c a c a b a b c a b c bc ca ab +-+-+-⎛⎫++++= ⎪⎝⎭， 即()()()2222228b c a c a b a b c bccaab+-+-+-++=，即()()()222222440b c a c a b a b c bccaab+-+-+--+-+=，即()()()2222220b c a c a b a b c bccaab----+-++=，即()()()()()()0b c a b c a c a b c a b a b c a b c bccaab-+---+--+++-++=，即()()()()0b c a ab c a b c a b c a b c abc-+----++++=⎡⎤⎣⎦，18即()22220b c a ab a b c abc-+⎡⎤--+=⎣⎦，即()()220b c a c a b abc-+⎡⎤--=⎣⎦， 即()()()0b c a c a b c a b abc-++--+=，所以0b c a -+=或0c a b +-=或0c a b -+=，即b a c +=或c a b +=或c b a +=．a b c 90o ．解法2：结合①式，由②式可得32232232214a b c bc ca ab ---++=， 变形，得()2221102424a b c abc -++=③又由①式得()21024a b c ++=，即()22210242a b c ab bc ca ++=-++，代入③式，得()110242102424ab bc ca abc --++=⎡⎤⎣⎦， 即()164096abc ab bc ca =++-．()()()()()331616161625616409625632160a b c abc ab bc ca a b c ---=-+++++-=-+⨯-=，所以16a =或16b =或16c =．结合①式可得b a c +=或c a b +=或c b a +=．a b c 90o ．19。

历年(95-10)年全国数学竞赛(联赛)分类题型详解 - 几何(1)选择题(30道题)1. 如果边长顺次为25、39、52与60的四边形内接于一圆，那么此圆的周长为［ ]A．62πB．63π C．64πD．65π1995年全国初中数学联赛试题答案: D详解：四个选择支表明，圆的周长存在且唯一，从而直径也存在且唯一．又由AB2＋AD2 ＝252＋602 ＝52×（52＋122）＝52×132＝(32＋42)×132 ＝392＋522 ＝BC2＋CD2故可取BD＝65为直径，得周长为65π，选D．2. 设AB是⊙O的一条弦，CD是⊙O的直径，且与弦AB相交，记M＝｜S△CAB－S△DAB｜，N＝2S△OAB，则[ ]A．M＞N B．M＝N C．M＜N D．M、N的大小关系不确定1995年全国初中数学联赛试题答案: B详解1: 不失一般性，设CE≥ED，在CE上取CF＝ED，则有OF＝OE，且S△ACE－S△ADE＝S△AEF＝2S△AOE．同理，S△BCE－S△BDE＝2S△BOE．相加，得S△ABC－S△DAB＝2S△OAB，即M＝N．选B．详解2: 若过C、D、O分别作AB的垂线（图3），CE⊥AB、DF⊥AB、OL⊥AB，垂足分别为E、F、L．连CF、DE，可得梯形CEDF．又由垂径分弦定理，知L是EF的中点．根据课本上做过的一道作业：梯形对角线中点的连线平行底边，并且等于两底差的一半，有｜CE－DF｜＝2OL．即M＝N．选B．3．如图，A是半径为1的圆O外的一点，OA=2，AB是圆O的切线，B是切点，弦BC∥OA，连结AC，则阴影部分的面积等于[ ]1996年全国初中数学联赛试题答案: B4．如果一个三角形的面积和周长都被一直线所平分，那么该直线必通过这个三角形的[ ]A．内心B．外心C．重心D．垂心1996年全国初中数学联赛试题答案: A5．如果20个点将某圆周20等分，那么顶点只能在这20个点中选取的正多边形的个数有[ ]A．4个B．8个 C．12个 D．24个1996年全国初中数学联赛试题答案: C6. 在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积等于（）（Ａ）12（Ｂ）14（Ｃ）16（Ｄ）181998年全国数学联赛试卷答案: C详解: 连ED，则又因为DE是△ABC两边中点连线，所以故选C．7．一个凸n边形的内角和小于1999°，那么n的最大值是（）．A．11 B．12 C．13 D．141999年全国初中数学竞赛答案: C8．在三角形ABC 中，D 是边BC 上的一点，已知AC=5，AD=6，BD=10，CD=5，那么三角形ABC 的面积是（ ）．A ．30B ．36C ．72D ．1251999年全国初中数学竞赛答案: B9．在正五边形ABCDE 所在的平面内能找到点P ，使得△PCD 与△BCD 的面积相等，并且△ABP 为等腰三角形，这样的不同的点P 的个数为（ ）．A ．2B ．3C ．4D ．51999年全国初中数学竞赛答案: D10. 设a ，b ，c 分别是△ABC 的三边的长，且cb a ba b a +++=，则它的内角∠A 、∠B 的关系是（ ）。