00 常用数学符号表

常用数学输入符号：≈ ≡ ≠ ＝≤≥ ＜＞≮≯∷ ±＋－× ÷／∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴//⊥‖ ∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔαβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯexp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数；b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin yacos x y，余弦函数反函数在x处的值，即x = cos yatan x y，正切函数反函数在x处的值，即x = tan yacot x y，余切函数反函数在x处的值，即x = cot yasec x y，正割函数反函数在x处的值，即x = sec yacsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在其上部。

数学上，有一组常在数学表达式中出现的符号。

数学工作者熟悉这些符号，不是每次使用都加以说明。

所以，对于数学初学者，下面的列表给出了很多常见的符号包括名称、读法和应用领域。

另外，第三栏有一个非正式的定义，第四栏有个简单的例子。

注意，有时候不同符号有相同含义，而有些符号在不同的上下文中有不同的含义。

注意：本条目含有特殊字符。

=等号x= y表示x和y是相同的东西或其值相等。

1 + 1 =2 等于所有领域≠不等号x≠ y表示x和y不是相同的的东西或数值。

1 ≠ 2不等于所有领域< >严格不等号x< y表示x小于y。

x> y表示x大于y。

3 < 45 > 4 小于，大于序理论≤≥不等号x≤ y表示x小于等于y。

x≥ y表示x大于等于y。

3 ≤ 4；5 ≤ 55 ≥ 4；5 ≥ 5小于等于，大于等于序理论+加号4 + 6 表示4 加6。

2 + 7 = 9 加算术−减号9 − 4 表示9 减4。

8 − 3 = 5减算术−3 表示3 的负数。

−(−5) = 5负算术补集A− B表示包含所有属于A但不属于B的元素的集合。

{1,2,4} − {1,3,4} = {2}减集合论×乘号3 ×4 表示3 乘以4。

7 ×8 = 56乘以算术直积X×Y表示所有第一个元素属于X，第二个元素属于Y的有序对的集合。

{1,2} ×{3,4} = {(1,3),(1,4),(2,3),(2,4)}… 和…的直积集合论叉乘u×v表示向量u和v的叉乘。

(1,2,5) × (3,4,−1) = (−22, 16, −2)叉乘向量代数÷/除号6 ÷3 或6 / 3 表示6 除以3。

2 ÷4 = 0.512/4 = 3除以算术√根号√x表示其平方为x的正数。

√4 = 2…的平方根实数复根号若用极坐标表示复数z= r exp(iφ)（满足-π < φ ≤ π），则√z= √r exp(iφ/2)。

加号和减号加减运算是人类最早掌握的两种数学运算，且载于人类最早的文字记载中。

古埃及的阿默斯纸草书就载有加号（Sign for Addition）及减号（ Sign for Subtraction）：向右走的两条腿“”是加号，而向左走的两条腿“”是减号。

后者于莫斯科纸草书中则表示“平方”。

古希腊的丢番图以两数并列表示相加，偶然亦以一斜线“∕”及曲线“”分别作加号和减号使用。

古印度人一般不用加号，只有在公元三世纪的巴赫沙里（Bakhshali）残简中以“yu”作加及“＋”作减。

中国古代因注重以工具计算，一般运算全在算筹或算盘上进行，只记录其结果，因此并无采用甚么数学符号，记录时用文字表达运算。

十五世纪阿拉伯人盖拉萨迪以两数并列”作减号。

作加而以一特别符号“s法国人许凯（1484）、意大利人帕乔利（1494）及十六世纪大多数学家都以拉丁词语plus（加）与minus （减）之首字母分别作加号（或p）和减号（或m）。

十五世纪后廿年之德国人是最早使用现代的加号“＋”与减号“－”。

德国德累斯顿（Dresden）图书馆所保存之手稿卷c.80(1486)中便正式使用了“＋”、“－”号。

而最先于印刷的书内使用加号“＋”与减号“－”的是捷克人维德曼（1489）。

从十五世纪末至整个十六世纪，意大利人仍以及作加减号。

到了1608年，德国人克拉维乌斯于罗马出版的《代数》一书内采用了“＋”“－”号，意大利人才开始采用这两符号，但到卡瓦列里时代已很纯熟。

此外，英国首个使用这两符号（1557）的是雷科德，而荷兰则于1637年由胡克引入这两符号，同时亦传入其它欧洲大陆国家，后渐流行于全世界。

乘号乘法（Multiplication）亦是最早产生的运算之一，且出现于人类最早的文字记载当中。

中国古人及古希腊的丢番图都不用乘号（Signs of multiplication），但后者则以两数并列表示相乘（与加法相同）。

印度的巴赫沙里残简中，把数排成表示；排成表示x x施蒂费尔于1545年出版的一本算术书内以大写字母M及D分别表示乘和除。

常用数学符号的输入与一些约定1、几何符号2、代数符号3、运算符号4、集合符号5、特殊符号特殊符号∑π（圆周率）＠＃☆★○●◎◇◆□■▓⊿※￥ΓΔΘΛΞΟΠΣΦΧΨΩ∏6、推理符号←↑→↓↖↗↘↙∴∵∶∷ÞÛÜ7、标点符号 ` ˉˇ¨、·｀＇8、其他& ; §℃№＄￡￥‰℉♂♀9、序号10、拉丁字母分数：12 13 23 14 34 15 25 35 45 22 32 33236＋22 6－22根式：2 3 5 32 43幂（指数）（上标）快捷键a 2 a 3 a 4 ax 2＋bx ＋c混合：a 12a 2a 32对数（下标）快捷键log 23 y ＝log 2x y ＝log 2xlog 123 y ＝log 12x y ＝log 22xy ＝log 2(x ＋1) y ＝log 2x ＋1 y ＝log 2ax 2＋bx －cy ＝log 2x ＋1x －126π3 π3{x | x ＝－π3＋2k π，k ∈R } [－π2＋2k π , π2＋2k π](k ∈Z )tan α＝sin αcos α 1＋2sin αcos αsin 2α－cos 2α向量符号→OB ，→OC ，→OA→AB ＋→AD→a ，→b ，→0排列组合符号A m n C mnA 24 C 24 椭圆、双曲线方程x 216＋y 29＝1 x 236＋y 249＝1 x 29－y 24＝1 y 216－x 29＝1．行列式和矩阵符号⎪⎪⎪⎪⎪⎪⎪⎪a 11a 12a 13a 21a 22a 23a 31a 32a 33⎪⎪⎪⎪⎪⎪⎪⎪2-101x-23-12⎪⎪⎪⎪1tan α tan α1⎝⎛⎭⎫324102 ⎝ ⎛⎭⎪⎪⎫-6-20-1-5-6-4-5-4 ⎝ ⎛⎭⎪⎪⎫13126271-5-43428-2-1-241-7线性方程组⎩⎨⎧4x ＋5y ＝03x －7y ＝0⎩⎪⎨⎪⎧a ＋b ＋c ＝0a －b －2c ＝02a －b ＋kc ＝0 ⎩⎪⎨⎪⎧a ＋3b －7c －8d ＝0 a ＋4b +3c ＋2d ＝03a －7b －2c －3d ＝02a ＋3b ＋4c ＋d ＝0⎩⎨⎧x 1＋2x 2－3x 3＝42x 1＋3x 2－5x 3＝74x 1＋3x 2－9x 3＝9⎝ ⎛⎭⎪⎫3x +1⎣⎢⎡⎦⎥⎤13，+∞ ⎝ ⎛⎭⎪⎫13，+∞ 4RateX ＋8RateX = 12RateX10∑i =15a i⎠⎛15f (x )⎠⎛15f (x )⎠⎜⎜⎛2001002x5dx A BAC z s上标字符下标字符˙1，˙2，˙3，˙4，˙5，˙6，˙7，˙8，˙9， ˙3˙7，˙37˙6Γ Δ Θ Λ Ξ Ο Π Σ Φ Χ Ψ Ωα β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω ∈ ∏ ∑ ∕ √ ∝ ∞ ∟ ∠ ∣ ∥ ∧ ∨ ∩ ∪ ∫ ∮ ∴ ∵ ∶ ∷ ∽ ≈ ≌ ≒ ≠ ≡ ≤ ≥ ≦ ≧ ≮ ≯ ⊕ ⊙ ⊥ ⊿ ⌒指数0123：º¹²³ 〃 ¼ ½ ¾ 符号 意义 ∞ 无穷大 PI 圆周率 |x| 函数的绝对值 ∪ 集合并 ∩ 集合交 ≥ 大于等于 ≤ 小于等于 ≡ 恒等于或同余 ln(x) 以e 为底的对数 lg(x) 以10为底的对数 floor(x) 上取整函数 ceil(x) 下取整函数 x mod y 求余数 {x} 小数部分 x - floor(x) ∫f(x)δx 不定积分 ∫[a:b]f(x)δx a 到b 的定积分∑[1≤k≤n]f(k)对n进行求和,可以拓广至很多情况，如：∑[n is prime][n < 10]f(n) ∑∑[1≤i≤j≤n]n^2 lim f(x) (x->?)求极限C(n:m)组合数,n中取m P(n:m)排列数m|n m整除n (m,n)=1 m与n互质a ∈ A a属于集合A Card(A)集合A中的元素个数|a| ⊥∽△∠∩∪≠∵∴≡±≥≤∈←↑→↓↖↗↘↙∥∧∨ &frac14; &frac12; &frac34;§①②③④⑤⑥⑦⑧⑨⑩αβγδεζηθικλμνξοπρστυφχψωⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏∑∕√∝∞∟∠∣∥∧∨∩∪∫∮∴∵∶∷∽≈≌≒≠≡≤≥≦≧≮≯⊕⊙⊥⊿⌒为了方便，也做些约定！ x的平方，可以打成x^2 （其它的以此类推） x+1的开方，可以打成√(x+1)，记住加括号； x分之一，可以输入1/x;如果是x+1分之一，请输入1/(x+1)，分子、分母请加括号 <> 或 >< 表示不等于例：a<>b 即 a不等于b； <= 表示小于等于（不大于）例：a<=b 即 a不大于b； >= 表示大于等于（不小于）例：a>=b 即 a不小于b； ^ 表示乘方例：a^b 即a的b次方 , 也可用于开根号，例： a^(1/2) 表示a的平方根 * 表示乘…… / 表示浮点除例：3/2=1.5 \ 表示整除例：3\2=1……1（）广义括号，允许多重嵌套，无大、中、小之分，优先级最高。

常用数学符号的输入与一些约定1、几何符号2、代数符号3、运算符号4、集合符号5、特殊符号特殊符号∑ π（圆周率）＠＃☆★○●◎◇◆□■▓⊿※￥Γ Δ Θ Λ Ξ Ο Π Σ Φ Χ Ψ Ω ∏6、推理符号← ↑ → ↓ ↖↗↘↙∴∵∶∷ÞÛÜ7、标点符号` ˉ ˇ ¨ 、· ｀＇8、其他& ; § ℃№ ＄￡￥‰ ℉♂♀9、序号10、拉丁字母分数：12 13 23 14 34 15 25 35 45 22 32 33236＋22 6－22根式：2 3 5 32 43幂（指数）（上标）快捷键a 2 a 3 a 4 ax 2＋bx ＋c混合：a 12a 2a 32对数（下标）快捷键log 23 y ＝log 2x y ＝log 2xlog 123 y ＝log 12x y ＝log 22xy ＝log 2(x ＋1) y ＝log 2x ＋1 y ＝log 2ax 2＋bx －cy ＝log 2x ＋1x －126π3 π3{x | x ＝－π3＋2k π，k ∈R } [－π2＋2k π , π2＋2k π](k ∈Z )tan α＝sin αcos α 1＋2sin αcos αsin 2α－cos 2α向量符号→OB ，→OC ，→OA→AB ＋→AD→a ，→b ，→0排列组合符号A m n C mnA 24 C 24 椭圆、双曲线方程x 216＋y 29＝1 x 236＋y 249＝1 x 29－y 24＝1 y 216－x 29＝1．行列式和矩阵符号⎪⎪⎪⎪⎪⎪⎪⎪a 11a 12a 13a 21a 22a 23a 31a 32a 33⎪⎪⎪⎪⎪⎪⎪⎪2-101x-23-12⎪⎪⎪⎪1tan α tan α1⎝⎛⎭⎫324102 ⎝ ⎛⎭⎪⎪⎫-6-20-1-5-6-4-5-4 ⎝ ⎛⎭⎪⎪⎫13126271-5-43428-2-1-241-7线性方程组⎩⎨⎧4x ＋5y ＝03x －7y ＝0⎩⎪⎨⎪⎧a ＋b ＋c ＝0a －b －2c ＝02a －b ＋kc ＝0 ⎩⎪⎨⎪⎧a ＋3b －7c －8d ＝0 a ＋4b +3c ＋2d ＝03a －7b －2c －3d ＝02a ＋3b ＋4c ＋d ＝0⎩⎨⎧x 1＋2x 2－3x 3＝42x 1＋3x 2－5x 3＝74x 1＋3x 2－9x 3＝9⎝ ⎛⎭⎪⎫3x +1⎣⎢⎡⎦⎥⎤13，+∞ ⎝ ⎛⎭⎪⎫13，+∞ 4RateX ＋8RateX = 12RateX10∑i =15a i⎠⎛15f (x )⎠⎛15f (x )⎠⎜⎜⎛2001002x5dx A BAC z s上标字符下标字符˙1，˙2，˙3，˙4，˙5，˙6，˙7，˙8，˙9， ˙3˙7，˙37˙6Γ Δ Θ Λ Ξ Ο Π Σ Φ Χ Ψ Ωα β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω ∈ ∏ ∑ ∕ √ ∝ ∞ ∟ ∠ ∣ ∥ ∧ ∨ ∩ ∪ ∫ ∮ ∴ ∵ ∶ ∷ ∽ ≈ ≌ ≒ ≠ ≡ ≤ ≥ ≦ ≧ ≮ ≯ ⊕ ⊙ ⊥ ⊿ ⌒指数0123：º¹²³ 〃 ¼ ½ ¾ 符号 意义 ∞ 无穷大 PI 圆周率 |x| 函数的绝对值 ∪ 集合并 ∩ 集合交 ≥ 大于等于 ≤ 小于等于 ≡ 恒等于或同余 ln(x) 以e 为底的对数 lg(x) 以10为底的对数 floor(x) 上取整函数 ceil(x) 下取整函数 x mod y 求余数 {x} 小数部分 x - floor(x) ∫f(x)δx 不定积分 ∫[a:b]f(x)δx a 到b 的定积分∑[1≤k≤n]f(k)对n进行求和,可以拓广至很多情况，如：∑[n is prime][n < 10]f(n) ∑∑[1≤i≤j≤n]n^2 lim f(x) (x->?)求极限C(n:m)组合数,n中取m P(n:m)排列数m|n m整除n (m,n)=1 m与n互质a ∈ A a属于集合A Card(A)集合A中的元素个数|a| ⊥ ∽ △ ∠ ∩ ∪ ≠ ∵ ∴ ≡ ± ≥ ≤ ∈ ← ↑ → ↓ ↖ ↗ ↘ ↙∥ ∧ ∨ &frac14; &frac12; &frac34;§ ①②③④⑤⑥⑦⑧⑨⑩ α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω ⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ∈∏∑∕√∝∞∟∠∣∥∧∨∩∪∫∮∴∵∶∷∽≈≌≒≠≡≤≥≦≧≮≯⊕⊙⊥⊿⌒ 为了方便，也做些约定！ x的平方，可以打成x^2 （其它的以此类推） x+1的开方，可以打成√(x+1)，记住加括号； x分之一，可以输入1/x;如果是x+1分之一，请输入1/(x+1)，分子、分母请加括号 <> 或 >< 表示不等于例：a<>b 即 a不等于b； <= 表示小于等于（不大于）例：a<=b 即 a不大于b； >= 表示大于等于（不小于）例：a>=b 即 a不小于b；^ 表示乘方例：a^b 即a的b次方 , 也可用于开根号，例： a^(1/2) 表示a的平方根 * 表示乘…… / 表示浮点除例：3/2=1.5 \ 表示整除例：3\2=1……1（）广义括号，允许多重嵌套，无大、中、小之分，优先级最高。

数学幼儿园教案：认识数学符号认识数学符号一、数学符号的重要性和作用数学符号是数学语言中不可或缺的一部分，它们能够简洁明确地表示数学概念和关系，提高数学表达的准确度和效率。

对于幼儿来说，认识数学符号是建立数学思维的基础，有助于他们理解和掌握数学知识，培养逻辑思维和抽象思维能力。

本教案将介绍一些常见的数学符号，帮助幼儿正确理解和运用它们。

二、常见的数学符号及其含义1. 加号（+）加号是加法运算的符号，表示两个数或数量相加。

比如：2 + 3 = 5，表示2和3相加的结果是5。

2. 减号（-）减号是减法运算的符号，表示一个数减去另一个数。

比如：5 - 2 = 3，表示5减去2的结果是3。

3. 乘号（×）乘号是乘法运算的符号，表示两个数或数量相乘。

比如：2 × 3 = 6，表示2和3相乘的结果是6。

4. 除号（÷）除号是除法运算的符号，表示一个数被另一个数整除。

比如：6 ÷ 2 = 3，表示6除以2的结果是3。

5. 等于号（=）等于号表示两个数或数量相等的关系。

比如：2 + 3 = 5，表示2加3等于5。

6. 大于号（>）、小于号（<）大于号用于比较两个数的大小关系，表示左边的数大于右边的数；小于号则表示相反的关系。

比如：4 > 2，表示4大于2。

7. 百分号（%）百分号表示百分数，常用于表示一个数相对于100的比例关系。

比如：50%表示数值为50的一半。

8. 开方符号（√）开方符号表示对一个数进行开方运算，求出该数的平方根。

比如：√9 = 3，表示对数值为9的数进行开方运算，结果是3。

9. 括号（()）括号用于表示计算次序，可以改变运算的先后顺序。

比如：2 × (3 + 4) = 14，表示先计算括号内的结果，再进行乘法运算。

10. 不等于号（≠）不等于号表示两个数或数量不相等的关系。

比如：2 + 3 ≠ 6，表示2加3不等于6。

三、数学符号的教学方法和策略1. 直观教学法适合于认识简单的数学符号，可以通过实物、图片或图形来直观地展示和教学。

数学符号自然数整数
数学符号是用来表示数学概念、关系和运算的特殊符号。

自然数是指从1开始的正整数集合，用符号N表示。

整数是由自然数、0和其相反数构成的数集，用符号Z表示。

在数学中，符号被广泛用于表示各种数学概念。

例如，自然数可以用N表示，整数可以用Z表示。

除此之外，还有许多其他符号用于表示不同的数学概念。

例如，加法运算可以用加号“+”表示，减法运算可以用减号“-”表示，乘法运算可以用乘号“×”或乘号“·”表示，除法运算可以用除号“÷”或分数线表示。

数学符号还可以用于表示数学关系。

例如，等于关系可以用等号“=”表示，大于关系可以用大于号“>”表示，小于关系可以用小于号“<”表示，大于等于关系可以用大于等于号“≥”表示，小于等于关系可以用小于等于号“≤”表示。

这些符号使得数学关系更加直观和易于理解。

此外，数学符号还可以用于表示数学运算。

例如，求和运算可以用希腊字母∑表示，积分运算可以用符号∫表示，微分运算可以用符号d 表示。

这些符号使得数学运算更加简洁和精确。

总之，数学符号在数学领域中起着重要的作用，它们帮助我们表示数
学概念、关系和运算，使得数学更加具体、准确和易于理解。

通过理解和运用这些符号，我们能够更好地理解和应用数学知识。

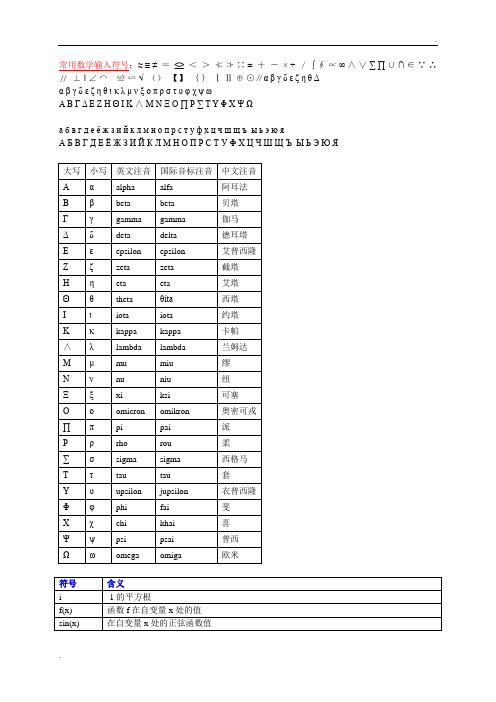
数学符号及读法大全经常使用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－× ÷／∫∮∝∞∧∨∑∏∪∩∈∵∴//⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e x a^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在其上部。

如j从1到100 的和可以表示成：。

这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积θvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。