第六章轮系解析
- 格式：pps
- 大小：424.00 KB
- 文档页数：26
下载文档原格式
合集下载
第六章轮系(2011.5.5)
2 4 H 1 3
哈尔滨工业大学特种传动研究室
2、按基本构件分：
中心轮与系杆的轴线位置均固定且重合，通常以 它们作为运动的输入和输出构件，故称其为周转 轮系的基本构件。 输入和输出构件——承受外力矩
表示方法： K-中心轮 H-系杆
哈尔滨工业大学特种传动研究室
？K-H型
2
H
O O
1 3
哈尔滨工业大学特种传动研究室
在各轮齿数已知的情况下，只要给定nA(ωA) 、(nk)ωk、 (nH) ωH中任意两项，即可求得第三项，从而可求出原周转轮 系中任意两构件之间的传动比。
哈尔滨工业大学特种传动研究室
利用公式计算时应注意：
H (1) iAK 是转化机构中A轮主动、K轮从动时的传动 比，其大小和符号完全按定轴轮系处理。正负号仅表明在 该轮系的转化机构中，齿轮A和齿轮K的转向关系。
i18
z 2 z4 z6 z8 n1 n8 z1 z 3 z5 z7
哈尔滨工业大学特种传动研究室
例题
如图所示的轮系中，已知各轮齿数，齿轮1为主动轮， 求传动比。
解：首末两轮轴线平行，可用画箭头法表示首末两轮 转向关系，该轮系传动比为：
z2 z 3 z4 z5 z6 n1 i16 z z z z 1 2 3 z 4 5 n6
⑵ 齿数比前的“”、“”号不仅表明在转化机构 中齿轮轮A和齿轮K的转向关系，而且将直接影响到周转 轮系传动比的大小和正负号。 ⑶ A、 K 和H是周转轮系中各基本构件的真实角 速度，且为代数量。
哈尔滨工业大学特种传动研究室
差动轮系 A、 K 和H三者需要有两个为已知值，才能求解。
行星轮系 其中一个中心轮固定(例如中心轮K固定，即K0)
第6章轮系例题精解.
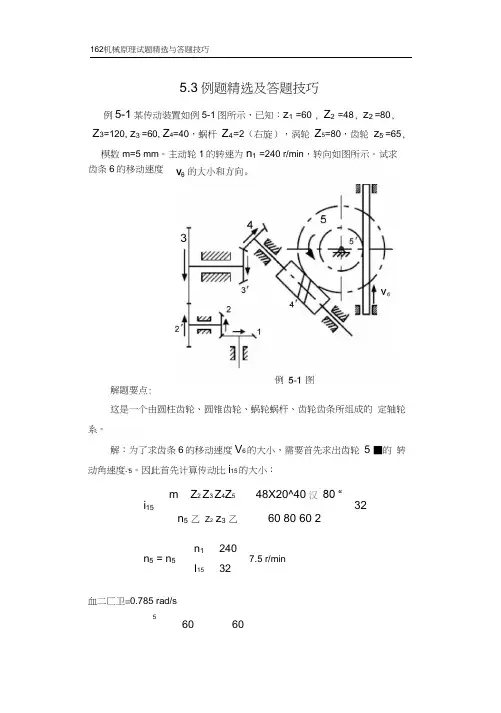
162机械原理试题精选与答题技巧560 605.3例题精选及答题技巧例5-1某传动装置如例5-1图所示，已知：z 1 =60 , Z 2 =48, z 2' =80,Z 3=120, z 3'=60, Z 4=40，蜗杆 Z 4'=2（右旋），涡轮 Z 5=80，齿轮 z 5'=65,模数m=5 mm 。
主动轮1的转速为n 1 =240 r/min ，转向如图所示。
试求解题要点:这是一个由圆柱齿轮、圆锥齿轮、蜗轮蜗杆、齿轮齿条所组成的 定轴轮系。
解：为了求齿条6的移动速度V 6的大小，需要首先求出齿轮 5 ■的 转动角速度-'5。
因此首先计算传动比i 15的大小：m Z 2 Z 3 Z 4Z 5 48X20^40汉 80 “ i 1532n 5 乙 Z 2 z 3 乙60 80 60 2n 1 240 n 5 = n 57.5 r/minI 1532血二匚卫=0.785 rad/s齿条6的移动速度第5章轮系163齿条6的移动速度等于齿轮5的分度圆线速度，即:1 1v6 =r5 5mz5 5 5 65 0.785=127.6 mm/s2 2齿条6的运动方向采用画箭头的方法确定如例5-1图所示。
例5-2如例5-2图所示，已知各轮齿数为Z1、Z2、Z3、Z4、Z、Z6，Z1为主动件，转向如图箭头所示，试求：1. 传动比im - 1 A ■ H二？（列出表达式）；2. 若已知各轮齿数Z1= Z2=Z4=Z5=20，Z3=40，Z6=60，求i1H的大小及转向。
解题要点:如例5-2图所示，从结构上看，此轮系由两部分组成，齿轮1、齿轮2、齿轮3组成定轴轮系，齿轮4、5、6及系杆H组成行星轮系，二者之间属串联关系。
齿轮3和齿轮4属同一构件。
解：1.根据上面分析，得到如下方程：14HZ1(1)3■H(2)丄7图5-26I 13Z2 Z3Z1 Z24■H164机械原理试题精选与答题技巧由式⑴与式⑵解得：讣=竺=色1+空灼HZ1 I 乙丿3.将 Z i =Z 4 =20, Z 3=40, Z 6=60 代入式⑶得：40 『60 ) i 1H =— 1 +—丨=820 i 20 丿转向如例5-2图所示。
第6章 轮系
第6章轮系本章主要介绍轮系的分类和应用，轮系传动比的计算方法。
由单对齿轮组成的齿轮机构功能单一，不能满足工程上的复杂要求，故常采用若干对齿轮，组成轮系来完成传动要求。
按轮系运动时轴线是否固定，将其分为两大类：（1）定轴轮系轮系运动时，所有齿轮轴线都固定的轮系，称为定轴轮系，如图1-1所示。
（2）行星轮系轮系运动时，至少有一个齿轮的轴线可以绕另一根齿轮的轴线转动，这样的轮系称为行星轮系。
轴线可动的齿轮称为行星轮，如图1-2中轮2，它既绕本身的轴线自转，又绕O1或O H公转。
轮1与轮3的轴线固定不动，称为太阳轮。
图1-1图1-21.1 定轴轮系定轴轮系分为两大类：一类是所有齿轮的轴线都相互平行，称为平行轴定轴轮系（亦称平面定轴轮系）；另一类轮系中有相交或交错的轴线，称之为非平行轴定轴轮系（亦称空间定轴轮系）。
轮系中，输入轴与输出轴的角速度或转速之比，称为轮系传动比。
计算传动比时，不仅要计算其数值大小，还要确定输入轴与输出轴的转向关系。
对于平行轴定轴轮系，其转向关系用正、负号表示：转向相同用正号，相反用负号。
对于非平行轴定轴轮系，各轮转动方向用箭头表示。
1.1.1 平行轴定轴轮系图1-1所示为各轴线平行的定轴轮系，输入轴与主动首轮1固联，输出轴与从动末轮5固联，所以该轮系传动比，就是输入轴与输出轴的转速比，其传动比i求法如下：（1）由图1-1所示轮系机构运动简图，可知齿轮动力传递线为：（1—2）＝（2′—3）＝（3′—4）＝（4—5）上式括号内是一对啮合齿轮，其中轮1、2′、3′、4为主动轮，2、3、4、5为从动轮；以 “—”所联两轮表示啮合，以“＝”所联两轮同轴运转，它们的转速相等。
（2） 传动比i 的大小()4543321245342312354433221511i i i i z z z z z z z zn n n n n n n n n n i ⋅⋅⋅=⋅⋅⋅-=⋅⋅⋅=='''''' 上式表明，该定轴齿轮系的传动比等于各对啮合齿轮传动比的连乘积，也等于各对啮合齿轮中各从动轮齿数的连乘积与各主动轮齿数的连乘积之比，其正负号取决于轮系中外啮合齿轮的对数。
第06章 轮系习题答案
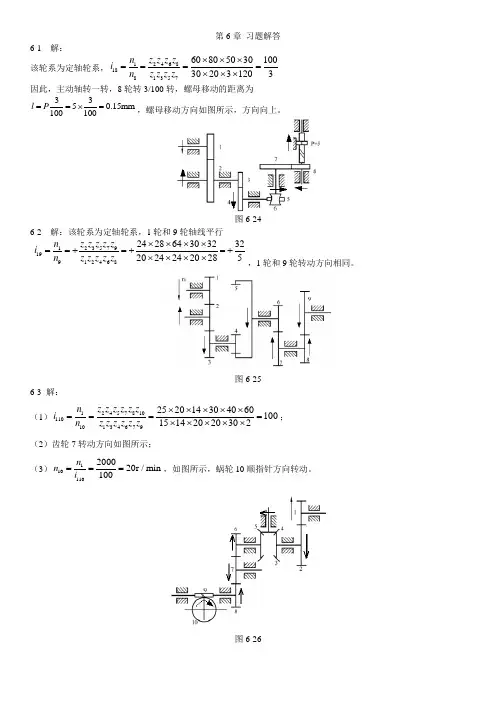
第6章 习题解答6-1 解： 该轮系为定轴轮系，24681188135760805030100302031203z z z z n i n z z z z ⨯⨯⨯====⨯⨯⨯ 因此，主动轴转一转，8轮转3/100转，螺母移动的距离为3350.15mm 100100l P ==⨯=，螺母移动方向如图所示，方向向上。
图6-246-2 解：该轮系为定轴轮系，1轮和9轮轴线平行 2357911991246824286430323220242420285z z z z z n i n z z z z z ⨯⨯⨯⨯==+=+=+⨯⨯⨯⨯，1轮和9轮转动方向相同。
图6-256-3 解：（1）245781011101013467925201430406010015142020302z z z z z z n i n z z z z z z ⨯⨯⨯⨯⨯====⨯⨯⨯⨯⨯； （2）齿轮7转动方向如图所示；（3）110110200020r /min 100n n i ===，如图所示，蜗轮10顺指针方向转动。
图6-266-4解：（1）该轮系是定轴轮系；图6-27（2）23411441234030549022018z z z n i n z z z ''⨯⨯====⨯⨯1414144016r /min 90n n i === （3）齿轮4的转动方向如图所示。
6-5 解：（1）该轮系为定轴轮系；234511551234403020542162015120z z z z n i n z z z z '''⨯⨯⨯====⨯⨯⨯ （2）查表5-14可得，42m =mm ，31z '=时，q=10，34344111()()2(1020)30mm 222a d d m q z ''=+=+=⨯⨯+=求3z '与4z 的中心距34?a '=（蜗杆的导程角tan 0.1γ=）； （3）手轮转一转，即1齿轮转一转时，鼓轮转1/216转，即1.67度。
第六章轮系和减速器
第六章 轮系和减速器
§6.1 轮系及分类 §6.2 定轴轮系 §6.3 行星轮系 §6.4 轮系的功用 §6.5 减速器
6.1 轮系及分类
§6.1 轮系及分类
在复杂的现代机械中，为了满足各种不同的需要，常常 采用一系列齿轮组成的传动系统。这种由一系列相互啮合的 齿轮（蜗杆、蜗轮）组成的传动系统即齿轮系。
如图所示车床上走 刀丝杆的三星轮换向机 构，扳动手柄可实现两 种传动方案。
6.4 轮系的功用
四、实现变速传动
在主动轴转速不变的情况 下，利用轮系可使从动轴获 得多种工作转速。如右图所 示的汽车变速箱，可使输出 轴得到4个档次的转速。
6.4 轮系的功用
五、用于对运动进行合成与分解
在差动齿轮系中，当给定两个基本构件的运动后，第三个构件的 运动是确定的。换而言之，第三个构件的运动是另外两个基本构件运 动的合成。
6.4 轮系的功用
二、获得大的传动比
如果采用多对齿轮组成的 齿轮系则可以很容易就获得较 大的传动比。只要适当选择齿 轮系中各对啮合齿轮的齿数， 即可得到所要求的传动比。在 行星齿轮系中，用较少的齿轮 即可获得很大的传动比，如右 图所示的轮系。
iH1 1000
6.4 轮系的功用
三、实现换向传动
在主动轴转向不变 的情况下，利用惰轮可 以改变从动轴的转向。
右图所示平面定轴齿轮系中各对齿轮 的传动比为：
i 12
z 1 2
2
z1
z i 2'3
'
2
3
3
Z
' 2
z 3' i 3'4
4
4
Z3/
i 45
z 4 5
5
z4
§6.1 轮系及分类 §6.2 定轴轮系 §6.3 行星轮系 §6.4 轮系的功用 §6.5 减速器
6.1 轮系及分类
§6.1 轮系及分类
在复杂的现代机械中，为了满足各种不同的需要，常常 采用一系列齿轮组成的传动系统。这种由一系列相互啮合的 齿轮（蜗杆、蜗轮）组成的传动系统即齿轮系。
如图所示车床上走 刀丝杆的三星轮换向机 构，扳动手柄可实现两 种传动方案。
6.4 轮系的功用
四、实现变速传动
在主动轴转速不变的情况 下，利用轮系可使从动轴获 得多种工作转速。如右图所 示的汽车变速箱，可使输出 轴得到4个档次的转速。
6.4 轮系的功用
五、用于对运动进行合成与分解
在差动齿轮系中，当给定两个基本构件的运动后，第三个构件的 运动是确定的。换而言之，第三个构件的运动是另外两个基本构件运 动的合成。
6.4 轮系的功用
二、获得大的传动比
如果采用多对齿轮组成的 齿轮系则可以很容易就获得较 大的传动比。只要适当选择齿 轮系中各对啮合齿轮的齿数， 即可得到所要求的传动比。在 行星齿轮系中，用较少的齿轮 即可获得很大的传动比，如右 图所示的轮系。
iH1 1000
6.4 轮系的功用
三、实现换向传动
在主动轴转向不变 的情况下，利用惰轮可 以改变从动轴的转向。
右图所示平面定轴齿轮系中各对齿轮 的传动比为：
i 12
z 1 2
2
z1
z i 2'3
'
2
3
3
Z
' 2
z 3' i 3'4
4
4
Z3/
i 45
z 4 5
5
z4
第六章轮系及其设计
定轴轮系传动比的计算的公式：
i1k
= 1 k
=
n1 =从1到k中各对齿轮传动比的连乘积 nk 所有末轮齿数的连乘积
= 所有首轮齿数的连乘积
2.首、末轮的转向 *平面定轴轮系：
3 4'
3'
24
5
1
i1k
= 1 k
= (−1)m
z2 zk z1 zk−1
m为外啮合的对数
*空间定轴轮系：
2
首末轮轴线平行 首末轮轴线不平行
3
2
o2
H
1 3
（2）特点：有一方面绕自身的几何轴线O2自转，另一方面 又随同转臂H绕几何轴线O1公转的 行星轮。
（3）类型：
F=2 （中心轮都是转动的） F=1 （有一个中心轮作了机架）
二、行星轮系传动比的计算
-H
2 2 3
H H
1
o1
1
3
2
o2
H
o1
1
3
2
o2
H
1 3
构件名称
转臂H 中心轮1 中心轮3
1+ z6
z4
3'
1
5
3
以上涉及到的都为两个中 心轮一个转臂的行星轮系， 称为2K-H型行星轮系。
求双重周转轮系的传动比i1H
解： 双周转轮系特点是，至少有一个行星轮同时绕三个轴线转动，主周转轮系 （5-H-6，和1-2-H-6）的行星架内有一个副周转轮系（2’-3-4-h-6） 行星轮系（ 5-H-6）
（2）
2'
i45
= 4 5
=
z5 z4
（4）
34
4' 5
第六章轮系
第6章 轮系
6.2 轮系的传动比 6.2.2 周转轮系的传动比
(2) 传动比计算方法 一般周转轮系转化机构的传动比 z2 zn 1 H H i1n n H z1 z n 1
行星轮系，ω1、ωn中一个为0(不妨设ωn＝0)，则上述通式改写为：
i1H n
(2) 传动比计算方法 一般周转轮系转化机构的传动比 z zn H i1H 1 2 n n H z1 z n 1 正号机构：
H 行星轮系传动比： i1H 1 i1n
i1nH>0的机构 i1H<1 iH1可能很大(0<i1H<1时)，也可能是负数(i1H<0时)； 效率总是小于转化机构效率，往往很低以至产生自锁； 可实现很大传动比，但不宜用于传递动力的场合。
ω3 2 H 1 3 ω1 2 H ωH 1 ω2 3
第6章 轮系
6.1 轮系的类型与应用 6.1.2 周转轮系
(2) 分类 根据自由度数的不同分类。 自由度为2的周转轮系差动轮系； 自由度为1的周转轮系行星轮系；
2 H 1 2 H 1
行星轮系
3
差动轮系
3
F=3n-2PL-PH F=3n-2PL-PH =3×3-2×3-2=1 =3×4-2×4-2=2
一个基本周转轮系至多只有三个中心轮
第6章 轮系
6.1 轮系的类型与应用 6.1.3 混合轮系
定义：由定轴轮系和周转轮系或者由两个以上的周转轮系所组成的轮系；
双排2K－H 型
定轴轮系
周转轮系
第6章 轮系
6.1 轮系的类型与应用 6.1.4 轮系的功能
第6章 轮系
任意从动齿轮的转速
n1k n1 n1 i1k
末端是螺旋传动
v nk Ph
末端是齿条传动
v nk πmz n1 z 1z 3 z 5 z k 1 πmz z2z 4z6 zk
v
n1
z 1z 3 z 5 z k 1 z 2z 4z 6 zk
z 1z 3 z 5 z k 1 Ph z2z 4z6 zk
L
z z z z k 1 L 1 3 5 Ph z2z 4z6 zk
L
z 1z 3 z 5 z k 1 πmz z2z 4z6 zk
汽车变速箱
世纪钟
６.１轮系分类及其应用特点 轮系——由多对齿轮所组成的传动系统称为齿轮系，简称轮系。 一、分类 按照传动时各齿轮的轴线位置是否固定，分为：定轴轮系、 周转轮系和混合轮系三大类。
定轴轮系——传动时所有齿轮的几何轴线位置均固定不变，这 种轮系统称为。
周转轮系——若轮系中，至少有一个齿轮的几何轴线不固定， 而绕其它齿轮的固定几何轴线回转。
1——表示首轮； k——表示末轮； m——外啮合的次数； i1k为+时，首轮与末轮转向相同； 为-时，首轮与末轮转向相反。
例 如下图所示轮系，已知各齿轮齿数及n1转向，求i19和判定 n９转向。
Ⅰ
Ⅱ Ⅲ
Ⅳ
n9
Ⅵ
Ⅴ
i19 i12i 23i 45i67i89 n1 n2 n 4 n6 n8 n 2 n3 n5 ，会增加齿轮的结构尺寸。采用轮系 可使结构紧凑，缩小传动空间，节约材料。
3.可以方便地实现变速和变向要求
4.可以实现运动的合成与分解
如采用行星轮系，可将两个独立的运动合成一个运动，或将一个运 动分解为两个独立的运动。
n1k n1 n1 i1k
末端是螺旋传动
v nk Ph
末端是齿条传动
v nk πmz n1 z 1z 3 z 5 z k 1 πmz z2z 4z6 zk
v
n1
z 1z 3 z 5 z k 1 z 2z 4z 6 zk
z 1z 3 z 5 z k 1 Ph z2z 4z6 zk
L
z z z z k 1 L 1 3 5 Ph z2z 4z6 zk
L
z 1z 3 z 5 z k 1 πmz z2z 4z6 zk
汽车变速箱
世纪钟
６.１轮系分类及其应用特点 轮系——由多对齿轮所组成的传动系统称为齿轮系，简称轮系。 一、分类 按照传动时各齿轮的轴线位置是否固定，分为：定轴轮系、 周转轮系和混合轮系三大类。
定轴轮系——传动时所有齿轮的几何轴线位置均固定不变，这 种轮系统称为。
周转轮系——若轮系中，至少有一个齿轮的几何轴线不固定， 而绕其它齿轮的固定几何轴线回转。
1——表示首轮； k——表示末轮； m——外啮合的次数； i1k为+时，首轮与末轮转向相同； 为-时，首轮与末轮转向相反。
例 如下图所示轮系，已知各齿轮齿数及n1转向，求i19和判定 n９转向。
Ⅰ
Ⅱ Ⅲ
Ⅳ
n9
Ⅵ
Ⅴ
i19 i12i 23i 45i67i89 n1 n2 n 4 n6 n8 n 2 n3 n5 ，会增加齿轮的结构尺寸。采用轮系 可使结构紧凑，缩小传动空间，节约材料。
3.可以方便地实现变速和变向要求
4.可以实现运动的合成与分解
如采用行星轮系，可将两个独立的运动合成一个运动，或将一个运 动分解为两个独立的运动。
第6章 轮系讲解学习
解：
n坯n9 分析题意可知：
1）齿坯由蜗轮9带动回转，所以
n刀64或n坯 1 n坯 n刀 64
2）滚刀回转1周，齿坯回转1个齿，即1/64周，所以
i刀坯 nn坯 刀zz12zz43zz65zz76zz98zz12zz43zz75zz98
3）由此可见
i7 5z z7 5z z1 2 z z4 3 z z9 8 n n 坯 刀 1 2 3 5 1 8 5 4 1 5 0 6 1 4 3 22 5 图 滚齿机工作台传动系统
1.平面定轴轮系传动比的计算 传动比大小的计算
i12
n1 n2
z2 z1
i23
n2 n3
z3 z2
i34
n3 n4
z4 z3
i45
n4 n5
z5 z4
i1 2 i2 3 i3 4 i4 5n n 1 2 n n 2 3 n n 3 4 n n 4 5z 2 z z2 3 z z3 4 z z4 5
解：
vn1zz2 1zz3 4ph50 5 2 6 5 8 3 7 8 35m 0/m min
Lz13p283831m 丝杠为右旋，砂轮架向右移动
图 磨床砂轮架进给机构
例：如图6-13所示轮系，齿轮1的转速为240r/min,求齿条10的 速度v10(齿轮9的模数为5mm) 。
解: 根据
d9=mz9 =5x65=325mm v10=v9 =πd9n9/(60×1000）= π×325×7.5/(60×1000） =0.128m/s v10的方向根据图示方向的判别竖直向下
定轴轮系
如图所示，黄色齿轮既自转又公转称为行星轮；绿色和白色齿轮和齿轮 的几何轴线的位置固定不动称为太阳轮，它们分别与行星轮相啮合；支持行 星轮作自转和公转的构件称为行星架或系杆。行星轮、太阳轮、行星架以及 机架组成周转轮系。一个基本周转轮系中，行星轮可有多个，太阳轮的数量 不多于两个，行星架只能有一个。
n坯n9 分析题意可知：
1）齿坯由蜗轮9带动回转，所以
n刀64或n坯 1 n坯 n刀 64
2）滚刀回转1周，齿坯回转1个齿，即1/64周，所以
i刀坯 nn坯 刀zz12zz43zz65zz76zz98zz12zz43zz75zz98
3）由此可见
i7 5z z7 5z z1 2 z z4 3 z z9 8 n n 坯 刀 1 2 3 5 1 8 5 4 1 5 0 6 1 4 3 22 5 图 滚齿机工作台传动系统
1.平面定轴轮系传动比的计算 传动比大小的计算
i12
n1 n2
z2 z1
i23
n2 n3
z3 z2
i34
n3 n4
z4 z3
i45
n4 n5
z5 z4
i1 2 i2 3 i3 4 i4 5n n 1 2 n n 2 3 n n 3 4 n n 4 5z 2 z z2 3 z z3 4 z z4 5
解：
vn1zz2 1zz3 4ph50 5 2 6 5 8 3 7 8 35m 0/m min
Lz13p283831m 丝杠为右旋，砂轮架向右移动
图 磨床砂轮架进给机构
例：如图6-13所示轮系，齿轮1的转速为240r/min,求齿条10的 速度v10(齿轮9的模数为5mm) 。
解: 根据
d9=mz9 =5x65=325mm v10=v9 =πd9n9/(60×1000）= π×325×7.5/(60×1000） =0.128m/s v10的方向根据图示方向的判别竖直向下
定轴轮系
如图所示，黄色齿轮既自转又公转称为行星轮；绿色和白色齿轮和齿轮 的几何轴线的位置固定不动称为太阳轮，它们分别与行星轮相啮合；支持行 星轮作自转和公转的构件称为行星架或系杆。行星轮、太阳轮、行星架以及 机架组成周转轮系。一个基本周转轮系中，行星轮可有多个，太阳轮的数量 不多于两个，行星架只能有一个。
机械原理轮系解析
定轴轮系3’-4-5-6
例7：图示车床电动三爪卡盘的行星减速装置，已知各轮齿 数： zl=6，z2= z2’=25，z3=57，z4=56，求传动比i14。
行星轮系1-2-3-H
行星轮系4-2’-2-3-H
例8：双重周转轮系，已知各轮齿数，求传动比 i lH。
星一特 轮个点 同副： 时周主 围转周 绕轮转 三系轮 根，系 轴至的 旋少行 转有星 。一架
三、混合轮系传动比计算
核心问题： 正确分解轮系组成，找到行星轮及支持其
运动的系杆。 有效组合，计算传动比
例5：图示龙门刨床 工作台的变速换向 机构。J、K为电磁 制动器，可分别刹 住构件A和3。已知 各轮齿数，求当分 别刹住A和3时的传 动比i1B。
用J刹住A时：
定轴轮系1-2-3-6 行星轮系3’-4-5-B
交错轴斜齿轮传动方向确定
例1：图示的定轴轮系中，主动轴
O1通过圆柱齿轮1、2、3与4传动轴 O4，再通过圆锥齿轮4’、5、5’与6 传动从动轴O6，轴O1与轴O6平行。 试确定轮系传动比i61。
例2：图示定轴轮系，在主动轴O1与从动轴O4之间 依次通过圆锥齿轮1与2、蜗杆2’与蜗轮3及圆柱齿轮 3’与4。设各轮齿数为z1=15，z2=30，z2’=2（头 数），z2=28，z3’=30，z4=45，主动轴 O1的转速 n1=200r／min，转向如图示，试确定从动轴O4转速 n4的大小与方向。
用K刹住时：
行星轮系1-2-3-A
行星轮系5-4-3’ -B
例6：电动卷扬机减速器（封闭式行星轮系），已知各轮齿 数z1=24，z2=48，z2’=30，z3=90，z3’=20，z4= 30，z5=80， 求传动比i 1H。若电动机转速n1=1450r／min，求卷筒转速nH。
例7：图示车床电动三爪卡盘的行星减速装置，已知各轮齿 数： zl=6，z2= z2’=25，z3=57，z4=56，求传动比i14。
行星轮系1-2-3-H
行星轮系4-2’-2-3-H
例8：双重周转轮系，已知各轮齿数，求传动比 i lH。
星一特 轮个点 同副： 时周主 围转周 绕轮转 三系轮 根，系 轴至的 旋少行 转有星 。一架
三、混合轮系传动比计算
核心问题： 正确分解轮系组成，找到行星轮及支持其
运动的系杆。 有效组合，计算传动比
例5：图示龙门刨床 工作台的变速换向 机构。J、K为电磁 制动器，可分别刹 住构件A和3。已知 各轮齿数，求当分 别刹住A和3时的传 动比i1B。
用J刹住A时：
定轴轮系1-2-3-6 行星轮系3’-4-5-B
交错轴斜齿轮传动方向确定
例1：图示的定轴轮系中，主动轴
O1通过圆柱齿轮1、2、3与4传动轴 O4，再通过圆锥齿轮4’、5、5’与6 传动从动轴O6，轴O1与轴O6平行。 试确定轮系传动比i61。
例2：图示定轴轮系，在主动轴O1与从动轴O4之间 依次通过圆锥齿轮1与2、蜗杆2’与蜗轮3及圆柱齿轮 3’与4。设各轮齿数为z1=15，z2=30，z2’=2（头 数），z2=28，z3’=30，z4=45，主动轴 O1的转速 n1=200r／min，转向如图示，试确定从动轴O4转速 n4的大小与方向。
用K刹住时：
行星轮系1-2-3-A
行星轮系5-4-3’ -B
例6：电动卷扬机减速器（封闭式行星轮系），已知各轮齿 数z1=24，z2=48，z2’=30，z3=90，z3’=20，z4= 30，z5=80， 求传动比i 1H。若电动机转速n1=1450r／min，求卷筒转速nH。
机械原理 第六章 轮系
• 齿轮1、2－2’、3和H 组成一差动周转轮系。 • 其余的齿轮6、1”－ 1’、5－5’、4组成一 定轴轮系。
2
H
(avi)
0
1 3
0
1 H 0
特点：① 有一个轴线不固定的 齿轮； ② 两个中心轮与系杆共轴线； ③ 一个中心轮固定为行星轮系； 中心轮都运动为差动轮系。
H
2 H
0 1 3 0 3
2
2
H
3
给整个周转轮系加一个与系杆H的角速度 大小相等、方向相反的公共角速度ωH
1 H
1
差 动 轮 系
实现大传动比的传动
例5：已知Z1=100 , Z2=101 , Z2′=100 , Z3=99 , 求iH1
H iH 1 10000 1
2．实现分路传动
单头滚刀 A B 9
齿坯 (avi) 右旋单头蜗杆 7
2 Ⅰ 1
8
3 4
6
5
机械式钟表机构
3．实现变速变向传动
y
x 1
n3Ⅲ
6 8 4
(avi)
输入轴与输出轴之间
的角速度之传动比:
i15
1 n1 5 n5
包含两个方面：大小与转向
i15
1 n1 5 n5
2
1
1 3
3' 4'
二、平面定轴轮系传动比的计算 轮系中各对啮合齿轮的传动比为：
4
5
5
z2 1 z3 z4 2 3' i12 = i3'4 = 2 = - z1 i23 = 3 = z2 4 = - z3' z5 4' i4‘5 = 5 = - z4' 且： 3 = 3 ' ， 4 = 4 '
第六章 轮系及其设计1
H 1 H 3
1 H 3 H
输入轴
输出轴
z3 1 H 3 H z1
构件名称 系杆Ｈ 中心轮１ 中心轮３
原周转轮系中 各构件的角速度
转化机构中各 构件的角速度
H H H H 0 1H 1 H
Ｈ 1
3
3H 3 H
2) 行星轮系 具有一个自由度
二、周转轮系的传动比 周转轮系传动比的计算方法（转化机构法）
周转轮系
反转法
定轴轮系 （转化机构）
定轴轮系传动 比计算公式
求解周转轮系 的传动比
周转轮系
ωH
给整个周转轮系加一个与系杆H的角速度 大小相等、方向相反的公共角速度ωH
构件名称 系杆Ｈ 中心轮１ 行星轮２ 中心轮３ 原周转轮系中 各构件的角速度 转化机构中各 构件的角速度
2）分列方程
n1 z 2 H n2 ' n H z3 z 4 1 i2' 4 , n2 z1 n4 n H z 2' z 3 2
3）联立求解：
3
H
2'
4
2' 4
OH
z1 n2 n1 z2
, n4 0 n2 n2
i1H
n1 z4 z2 14 ( 1) nH z2 z1 9
H
2
1 H 解：i 1 i1H 3 H
H 13
1 3
z3 80 2 z1 40
i1H
z3 1 i 1 3 z1
H 13
例6-２
z1 100 z2 101 z2 100 z3 99
求 iH 1
第六章轮系及其传动比计算
第六章轮系及其传动比计算6.1引言轮系是指由若干个齿轮组成的一种传动装置，在机械设备中起着重要的作用。
轮系的传动比是指输入轴和输出轴的转速之比，是轮系设计的重要参数之一、本章将介绍轮系的基本概念和传动比的计算方法。
6.2轮系的基本概念轮系由多个齿轮组成，每个齿轮都有一个输入轴和一个输出轴。
输入轴的转速通过齿轮的啮合传递给下一个齿轮，最终传递到输出轴。
在一个轮系中，有一个输入轴和一个输出轴，其它齿轮都是通过啮合传递转速。
在一个轮系中，齿轮的直径与其转速成反比，即直径越大，转速越小。
齿轮之间的啮合关系可以用一个传动比来描述，传动比是输出轴的转速与输入轴的转速之比。
6.3传动比的计算方法传动比的计算方法可分为两种：直接计算法和间接计算法。
6.3.1直接计算法直接计算法是根据齿轮的齿数和直径来计算传动比。
当一组齿轮串联时，传动比等于每个齿轮的齿数比的乘积。
当一组齿轮并联时，传动比等于每个齿轮的齿数比的和。
例如，一个轮系由两个齿轮组成，第一个齿轮的齿数为20，第二个齿轮的齿数为40。
则传动比为40/20=2使用直接计算法需要知道每个齿轮的齿数，因此适用于已知齿轮参数的情况。
6.3.2间接计算法间接计算法是通过测量轮系的输入轴和输出轴的转速来计算传动比。
该方法通过使用转速计或测速仪来测量转速，然后将测得的输入轴转速和输出轴转速之比作为传动比。
例如，通过测量得到输入轴转速为1000rpm，输出轴转速为500rpm，则传动比为500/1000=0.5间接计算法适用于无法直接测量齿轮参数的情况，但需要准确测量转速。
6.4小结本章介绍了轮系的基本概念和传动比的计算方法。
轮系是由多个齿轮组成的传动装置，传动比是描述轮系传动关系的重要参数。
传动比可通过直接计算法和间接计算法来计算。
直接计算法适用于已知齿轮参数的情况，而间接计算法适用于通过测量转速来计算传动比的情况。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章轮系
§6-1 轮系及其分类
轮系是由一系列齿轮所组成的传动装置。
定义：这种由一系列齿轮组成的传动系统称为轮系。
它通常介于原动机和执行机构之间，把原动机的运动和动力传给执行机构。
工程实际中常用其实现变速、换向和大功率传动等，具有非常广泛的应用。
轮系的类型
定轴轮系周转轮系混合轮系
1、定轴轮系
定义：组成轮系的所有齿
轮几何轴线的位置在运转
过程中均固定不变的轮系，
称为定轴轮系，又称为普
通轮系。
2、周转轮系
定义：组成轮系的齿轮中至少有一个齿轮几何轴线的位置不固定，而是绕着其它定轴齿轮轴线回转的轮系，称为周转轮系。
周转轮系组成：2—行星轮
1、3—中心轮
H—系杆或行星架
轮1与轮3
轴线重合
周转轮系的分类
1. 根据周转轮系所具有的自由度数目不同
(1)行星轮系
周转轮系中，若将中心轮3（或1）固定，则整个轮系的自由度为1。
这种自由度为1的周转轮系称为行星轮系。
为了确定该轮系的运动，只需要给定轮系中一个构件以独立的运动规律即可。
(2)差动轮系
周转轮系中，若中心轮1和3均不固定，则整个轮系的自由度为2。
这种自由度为2的周转轮系称为差动轮系。
为了使其具有确定的运动，需要两个原动件。
2. 根据周转轮系中基本构件的不同
(1)2K-H型周转轮系单排式双排式
双排式(2)3K型周转轮系具有三个中心轮
的周转轮系
一个周转轮系由行星轮、系杆和中心轮等几部分组成，其中，中心轮和系杆的运转轴线重合。
§6－2 定轴轮系的传动比
1、传动比定义
轮系中输入轴的角速度（或转速）与输出轴的角速度（或转速）之比，即：
2、一对齿轮的传动比
1
22112z z i ±==ωω正号：表示转向相同，用于内啮合
负号：表示转向相反，用于外啮合
3、传动比大小的计算
举例说明传动比计算
●主、从动轮转向关系的确
定
1、首末两轴平行，用“+”、“-”表示。
4——惰轮不改变传动比的大小，
但改变轮系的转向
2、首末两轴不平行
用箭头表示
所有主动轮齿数的乘积
所有从动轮齿数的乘积定轴轮系传动比
3、所有轴线都平行
所有主动轮齿数的乘积所有从动轮齿数的乘积m i )1(51-==ωωm ——外啮合的次数
4、所有齿轮的几何轴线不都平行，但首、尾两轮的轴线互相平行
仍可在传动比的计算结果中加上"+"、"-"号来表示主、从动轮的转向关系。
§6-3 周转轮系传动比
反转法
假想给整个轮系加上一
个公共的角速度(-ωH )，
据相对运动原理，各构
件之间的相对运动关系
并不改变，但此时系杆
的角速度就变成了ωH -ωH =0，即系杆可视为静止不动。
于是，周转轮系就转化成了一个假想的定轴轮系，通常称这个假想的定轴轮系为周转轮系的转化机构。
13313113)1(Z Z i H H H H H ⋅'-=--==ωωωωωω
)(z f i
H
B H A H B
H A H AB
±=--==ωωωωωω例1：图示为一大传动比的减速器，Z 1=100，Z 2=101，Z 2'=100，Z 3=99求：输入件H 对输出件1的传动比i H1
2
H
13
2'
10000
100
1009910111
111=⨯⨯-
==
H
H i i 若Z 1=99
100
1-=H i 周转轮系传动比正负是计算出来的，而不是判断出来的。
周转轮系转化机构传动比的一般公式：
例2：下图所示的轮系中，已知各轮的齿数为：
试求传动比i1H
解：这是一个双排2K-H型行星轮系。
其转化机构的传动比为
由于 3=0，故得
计算结果i1H为正值，说明系杆与中心轮1转向相同。
例3：如下图所示的轮系中，已知各轮的齿数为：，
又n1=250r/min
转向如图所示。
试求系杆的转速n H的大小和方向。
解：这是一个由锥齿轮所组成的
周转轮系。
先计算其转化机构的
传动比。
已知值代入上式
结果为正，表明系杆H的转向与
齿轮1相同，与齿轮3相反。
§6-4 复合轮系传动比
在计算混合轮系传动比时，既不能将整个轮系作为定轴轮系来处理，也不能对整个机构采用转化机构的办法。
计算混合轮系传动比的正确方法是：
（1）首先将各个基本轮系正确地区分开来。
（2）分别列出计算各基本轮系传动比的方程式。
（3）找出各基本轮系之间的联系。
（4）将各基本轮系传动比方程式联立求解，即可求得混合轮系的传动比。
具体划分方法：
先找行星轮，即找出那些几何轴线位置不固定而是绕其它定轴齿轮几何轴线转动的齿轮；找到行星轮后，支承行星轮的构件即为系杆；而几何轴线与系杆重合且直接与行星轮相啮合的定轴齿轮就是中心轮。
这一由行星轮、系杆、中心轮所组成的轮系，就是一个基本的周转轮系。
区分各个基本的周转轮系后，剩余的那些由定轴齿轮所组成的部分就是定轴轮系。
例4：在图所示的轮系中，设已知各轮的齿数为：
试求轴Ⅰ、轴Ⅱ之间的传动比。
解：这是一个混合轮系。
（1）首先区分各个基本轮系：
1-2-3-H 周转轮系
4-4‘-5-1’-3‘定轴轮系
（2）分别列出各基本轮系传动
比的计算式：
在1-2-3-H 中
即(a)
在4-4‘-5-1’-3‘中
（b）
(c)
（3）联系条件
代入（a）式得
从而可求得负号表明Ⅰ、Ⅱ两轴转向相反
二、轮系的应用①实现大传动比传动
所有主动轮齿数的乘积
所有从动轮齿数的乘积m i )1(51-==ωω②实现变速、换向传动③实现结构紧凑的大功率传动在周转轮系中，多采用多个行星轮的结构形式，各行星轮均匀地分布在中心轮四周，如图所示。
这样，载荷由多对齿轮承受，可大大提高承载能力；又因多个行星轮均匀分布，可大大改善受力状况此外，采用内啮合又有效地利用了空间，加之其输入轴与输出轴共线，可减小径向尺寸。
因此可在结构紧凑的条件下，实现大功率传动。
④实现多分路传动
机械式钟表机构就是一例⑤实现运动的合成与分解
利用差动轮系的双自由度特点，可把两个运动合成为一个运动。
图示的差动轮系就常被用来进行运动的合成。
差动轮系不仅能将两个独立地运动合成为一个运动，而且还可将一个基本构件的主动转动，按所需比例分解成另两个基本构件的不同运动。
汽车后桥的差速器就利用了差动轮系的这一特性。
§6-5 行星轮系各轮齿数和行星
轮数的选择
行星轮系
1、传动比条件
1
3
13
1
1
1
Z
Z
i
i H
H
+
=
-
=1
1
3
)1
(Z
i
Z
H
-
=
2、同心条件
2
3
2
1
r
r
r
r-
=
+即
2
)
(
2
)
(
2
3
2
1
z
z
m
z
z
m-
=
+
2
)2
(
2
1
1
1
3
2
-
=
-
=H
i
z
z
z
z
表明两中心轮齿数应同时为偶数或同为奇数
3、装配条件如图：设k ——均布的行星轮数
k π
2——相邻中心轮的夹角
将第一个行星轮在位置Ⅰ装入，并
固定中心轮3，再沿逆时针将行星架
转过到达位置Ⅱ。
此时，中心轮1转过k
H πϕ2=1
ϕ由于H H H i k 1111/2===ωωπϕϕϕ则H i k
112πϕ=如果这时在位置Ⅰ又能装入第二个行星轮，则中心轮1
在位置Ⅰ的轮齿相位应与它回转之前在该位置时的
轮齿相位完全相同，即必须刚好是个轮齿（即个周节）所对应的中心角。
1ϕ1ϕγγ
)2(1
1z πγϕ=解得k
z z i k z H 2111+==γ4、邻接条件
)
(2sin )(2*221m h r k r r a +>+π
k
h k z z a
π
π
sin 12sin *12--<
为了设计时便于选择各轮齿数，常把前三个条件合并为一个总的配齿公式。
H H H i k z i z i z z z z z 1111111321:)1(:2)2(::::--=γ。