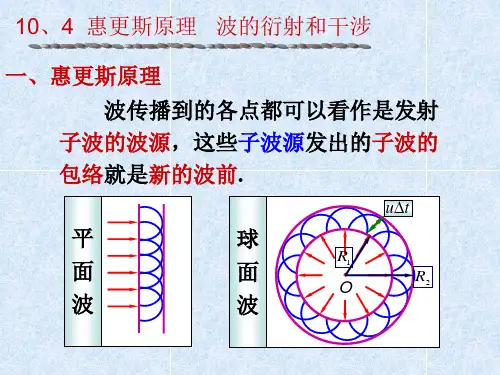
惠更斯原理

惠更斯原理可以说明波的衍射现象
1弗里德曼-赫伯特-惠更斯原理介绍
弗里德曼-赫伯特-惠更斯(Friedmann-Herbert-Huygens)原理是描述波、振动、传播等自由空间中的现象并产生具有哲学意义的一种物理学原理。

它把波描述为传播的小尺寸的圆形或椭圆形的包含着有限的能量的圆波，它们在自由空间中向各个方向传播。

这样就渐渐产生了空间中分布的波，这便是波的扩散或衍射。

2弗里德曼-赫伯特-惠更斯原理的定义
弗里德曼-赫伯特-惠更斯原理可定义为：在每个点，波源发射出的波在任意方向上都能同时传播，前面传播的不受后面新传播的波方向的影响，从而形成扩散或者说发散的波。

3弗里德曼-赫伯特-惠更斯原理的运用
弗里德曼-赫伯特-惠更斯原理可以用来解释一些物理现象，如声波的扩散现象。

当声波源发射出声波时，声波在扩散向它周围的自由空间中，就同时发散投射出去，这与弗里德曼-赫伯特-惠更斯原理是一致的。

此外，同样可以用弗里德曼-赫伯特-惠更斯原理来解释光波的衍射，即当光源发出光线时，光线是同时投射沿着入射面上各个方向，就会发生衍射现象，而这种衍射现象也是由弗里德曼-赫伯特-惠更斯原理得出的结果。

4结论
从上面可以看出，弗里德曼-赫伯特-惠更斯原理不仅可以用来解释声音的扩散现象，还可以用来解释光波的衍射现象，从而帮助我们了解自由空间中的波的传播行为。

同时，也可以作为物理学上一种比较重要的原理，用于研究波的传播、振动及其他相关现象。

总之，弗里德曼-赫伯特-惠更斯原理给我们带来了诸多具有指导意义的理论，在物理学上有其深奥而重要的意义。

惠更斯原理解释衍射现象引言衍射是物理学中一个重要的现象，它描述了当光线通过一个障碍物或者通过一个边缘时，发生的弯曲和扩散。

这个现象可以通过惠更斯原理来解释和理解。

惠更斯原理认为，每个点都可以看作是发射出波的波源，这些波在传播过程中相互干涉，形成新的波前。

在本文中，我们将详细说明惠更斯原理以及如何利用该原理解释衍射现象。

惠更斯原理的基本概念惠更斯原理是由法国物理学家惠更斯在17世纪提出的。

该原理认为，光线传播过程中，每个点都可以看作是发出波的波源。

在传播过程中，波会沿着各个方向传播，而波前则是波传播线上各个点的集合。

惠更斯原理的核心思想是，波会在传播过程中与其他波相互干涉，形成新的波前。

衍射现象的解释衍射现象可以被理解为波在通过障碍物或者经过边缘时产生的干涉现象。

当光线通过一个具有边缘或者孔径的障碍物时，波的传播会受到一定程度的限制和干涉，导致光线的扩散和弯曲。

这种现象就是衍射。

惠更斯原理可以很好地解释衍射现象。

惠更斯原理认为，波将在波前上的每一个点发出次波作为次波源。

这些次波源在传播过程中相互干涉，并产生新的波前。

当波在通过一个边缘时，边缘上的每个点都可以看作是一个次波源。

这些次波源发出的次波将以不同的相位和振幅发生干涉，产生一个新的波前。

这个新的波前将继续传播，并将波的能量扩散到边缘之外的区域，从而形成衍射现象。

衍射的实际应用衍射现象在光学和声学领域有许多实际应用。

以下是一些常见的应用：1.衍射光栅：衍射光栅是一种具有周期性结构的光学元件，它利用衍射现象将光分散成不同的颜色。

衍射光栅广泛应用于光谱仪、激光器和光通信等领域。

2.衍射声纳：衍射现象也存在于声学领域。

声波在通过边缘或孔径时会产生衍射现象，导致声波的传播方向发生变化。

基于衍射原理的声纳技术被广泛应用于水下通信和探测等领域。

3.衍射成像：衍射现象可以用于成像。

例如，透过窄缝或小孔的光线经过衍射后，可以在屏幕上形成干涉条纹。

基于这种原理，人们可以用衍射成像技术观察微小的细节和结构。

什么是惠更斯原理惠更斯原理是光学中的一个重要原理，它是由17世纪法国科学家惠更斯提出的。

惠更斯原理主要描述了光的传播规律，对于解释光的传播和衍射现象有着重要的意义。

在光学领域中，惠更斯原理被广泛应用于解释光的传播、干涉和衍射现象，对于理解光学现象有着重要的作用。

惠更斯原理的核心思想是，每个点上的波前都可以看作是次波源，这些次波源发出的波是波前上各点的相干波。

当波在传播过程中遇到障碍物或有限的孔径时，波会发生衍射现象，这时波的传播路径并不是沿直线传播，而是出现了弯曲的现象。

这种现象可以用惠更斯原理来解释，即波的每个点都可以看作是次波源，这些次波源发出的波相互叠加形成新的波前，从而产生了衍射现象。

惠更斯原理可以很好地解释光的传播规律，特别是对于光的干涉和衍射现象有着重要的意义。

在干涉现象中，当两条光线相遇时，它们会相互叠加形成干涉条纹，这种现象也可以用惠更斯原理来解释。

惠更斯原理认为，波的每个点都可以看作是次波源，这些次波源发出的波相互叠加形成了新的波前，从而产生了干涉现象。

在衍射现象中，当光线通过一个有限的孔径或遇到障碍物时，光会发生弯曲和扩散的现象，这也可以用惠更斯原理来解释。

惠更斯原理认为，波的每个点都可以看作是次波源，这些次波源发出的波相互叠加形成了新的波前，从而产生了衍射现象。

因此，惠更斯原理对于解释光的传播、干涉和衍射现象有着重要的作用。

除了在光学领域中的应用，惠更斯原理在波动理论中也有着广泛的应用。

惠更斯原理不仅可以解释光的传播规律，还可以解释其他波动现象，如声波、水波等的传播规律。

因此，惠更斯原理是波动理论中一个非常重要的原理，对于理解波动现象有着重要的作用。

总之，惠更斯原理是光学和波动理论中的一个重要原理，它描述了波的每个点都可以看作是次波源，这些次波源发出的波相互叠加形成了新的波前，从而产生了光的传播、干涉和衍射现象。

惠更斯原理对于解释光学和波动现象有着重要的意义，是光学和波动理论中不可或缺的一部分。

惠更斯原理的适用范围
惠更斯原理是光学中的基本原理，适用范围包括以下几个方面：
1. 光的传播：惠更斯原理用于描述光的传播过程。

根据该原理，光在空间中传播时是以波的形式进行的，光线在各点的传播方向上具有相同的波前面。

利用这个原理可以解释光的反射、折射、衍射等现象。

2. 光的反射：惠更斯原理可以用于解释光的反射现象。

根据该原理，入射光线在反射面上的各点作为次级波源发出的波前面，能够合成一条反射光线。

惠更斯原理可以用于推导光的反射定律，即入射角等于反射角。

3. 光的折射：惠更斯原理可以用于解释光的折射现象。

根据该原理，入射光线在折射界面上的各点作为次级波源发出的波前面，能够合成一条折射光线。

惠更斯原理可以用于推导光的折射定律，即折射角满足较李斯定律。

4. 光的衍射：惠更斯原理可以用于解释光的衍射现象。

根据该原理，光通过一道狭缝或物体边缘时，每个狭缝或边缘上的点都可以看作次级波源，通过这些次级波源发出的波前面进行叠加后形成衍射波前面。

利用这个原理可以解释衍射的干涉条纹、衍射狭缝等现象。

5. 光的干涉：惠更斯原理可以用于解释光的干涉现象。

根据该原理，当两束光线相遇时，根据每个点都可以看作次级波源，通过这些次级波源发出的波前面进行叠加后形成干涉波前面。

利用这个原理可以解释干涉的干涉条纹、干涉现象等。

总之，惠更斯原理适用于光学中的传播、反射、折射、衍射、干涉等现象的解释和分析。

惠更斯原理波惠更斯原理是光波传播的基本原理之一。

根据惠更斯原理，光波在传播过程中遵循着波的传播规律，即光波传播是通过波前的连续传播而实现的。

本文将详细介绍惠更斯原理及其在光学领域的应用。

我们来了解一下惠更斯原理的基本概念。

惠更斯原理是法国物理学家惠更斯在17世纪提出的，他认为光波的传播可以看作是波前的连续传播。

所谓波前，指的是波的前沿，即波的传播方向上每一点上的振动状态。

根据惠更斯原理，波在传播过程中，波前上每一点都可以看作是一个新的波源，它发出的次波与其他波源发出的次波叠加后形成新的波前，从而实现波的传播。

这个过程就像是在水面上扔石子，石子落入水中会产生涟漪，涟漪的波前会向四周扩散，不断形成新的波前，从而实现波的传播。

惠更斯原理在光学领域的应用非常广泛。

其中，最著名的应用之一就是解释光的直线传播。

根据惠更斯原理，光波在传播过程中，波前上的每一点都可以看作是一个新的波源，它发出的次波与其他波源发出的次波叠加后形成新的波前。

当光波传播到介质的边界面时，由于介质的性质不同，波速会发生改变。

根据惠更斯原理，波前上每一点都可以看作是一个新的波源，这些新的波源会发出次波，而这些次波会受到介质的影响，根据介质的性质不同，次波的传播速度也会不同。

当这些次波叠加后形成新的波前时，新的波前上的每一点都具有相同的相位，从而形成了一个新的波。

这个新的波将按照惠更斯原理的规律继续传播，直到最终到达观察者的位置。

因此，根据惠更斯原理，光波在传播过程中会沿着直线传播。

除了解释光的直线传播外，惠更斯原理还可以用来解释光的反射和折射现象。

当光波传播到平滑的反射面时，根据惠更斯原理，波前上的每一点都可以看作是一个新的波源，它发出的次波与其他波源发出的次波叠加后形成新的波前。

这些次波在反射面上发生反射，根据反射定律，反射角等于入射角，次波的传播速度保持不变。

当这些次波叠加后形成新的波前时，新的波前上的每一点都具有相同的相位，从而形成了一个新的波。

1惠更斯－菲涅尔原理⏹ 惠更斯－菲涅耳原理可以表述如下：⏹ 波前上每一个面元都可看成是新的振动中心，它们发出次波（频率与入射波相同）; ⏹ 在空间某一点P 的振动是所有这些次波在该点的相干迭加。

⏹ 是相干叠加→复振幅叠加 ⏹ 如图所示。

点光源S 在波面∑’ 上任一点Q 产生的复振幅为 ⏹ 式中，A 是离点光源单位距离处的振幅， ⏹ R 是波面∑’的半径。

⏹ 在Q 点处取面元d σ，面元发出的子波在P 点产生的复振幅与在面元上的复振幅 、面元大小和倾斜因子K(θ)成正比。

⏹ 面元d σ在P 点产生的复振幅可以表示为⏹ K(θ)表示子波的振幅随面元法线与QP 的夹角θ的变化。

（ θ称为衍射角） ⏹ c 为一常数,r=QP 。

⏹ 菲涅耳假设：当时θ=0 ，倾斜因子K 有最大值，随着增加θ↑ ，K 减小， ⏹ 当θ≥π/2时，K=0。

(基尔霍夫理论证明不正确)⏹ 对P 点产生作用的将是波面∑’中界于z z’范围内的波面∑上的面元发出的子波。

⏹ 则：⏹ 此即为惠更斯－菲涅耳原理的菲涅耳表达式，此关系式还可推广为（5－4）式， ⏹ 即⏹ 若： ⏹ 有： 2基尔霍夫衍射理论⏹ 基尔霍夫理论，只适用于标量波的衍射，故又称标量衍射理论。

3巴俾涅（Babinet ）原理 即两个互补屏单独产生的衍射场的复振幅之和等于没有屏时的复振幅。

在 的那些点，两个互补屏单独产生的强度相等。

菲涅耳衍射是普遍的，夫琅和费衍射是菲涅耳衍射的特例⏹ 基尔霍夫衍射公式的近似：⏹ 1.傍轴近似：入射光垂直孔径面 ⏹ 2.菲涅耳近似 ：S ()ikR RA E Q exp ~→= ()()()()σθd r ikr R ikR A cK P E d exp exp ~→= ()()()()⎰⎰∑=σθd rikr K R ikR A c P E exp exp ~ ()ikR RA E Q exp ~ =()()()()⎰⎰∑=σθd K rikr Q E c P E exp ~~ ()0P ~=E ()111,1z r K ≈=θ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-+=2121211211z y y x x z r⏹ 3.夫琅和费近似：⏹ 4.菲涅耳衍射公式：⏹ 5.夫琅和费衍射公式： ⏹ 即只有在很远距离上才能观察到夫琅和费衍射条纹，在实验室中很难实现。

惠更斯原理解释折射惠更斯原理是光的波动理论的基础，它对于解释光的传播和折射现象起着重要的作用。

折射是光线从一种介质射入另一种介质时由于介质的不同而改变传播方向的现象。

在解释折射现象时，惠更斯原理提供了一种简洁而准确的描述。

首先，我们来了解一下惠更斯原理的基本内容。

惠更斯原理是由17世纪的法国物理学家惠更斯提出的，它的核心思想是每个波前上的每一点都可以作为次波源，次波源发出的次波是在原来波前的基础上向前传播的。

这一思想在解释光的传播和折射现象时具有重要意义。

在折射现象中，当一束光线从一种介质射入另一种介质时，由于介质的光密度不同，光线的传播速度也不同，从而导致光线的传播方向发生改变。

根据惠更斯原理，我们可以通过构建次波源的方法来解释这一现象。

假设光线从空气射入水中，水的光密度大于空气，光速度减小。

在光线射入水中的过程中，我们可以将波前上的每一点都看作是次波源，这些次波源发出的次波在原来波前的基础上向前传播。

由于水的光密度大，光速度小，次波在水中的传播速度比在空气中慢，因此次波在水中的传播方向会发生改变，从而导致光线整体的传播方向也发生改变，这就是折射现象的基本原理。

通过惠更斯原理的解释，我们可以更好地理解折射现象的发生机制。

惠更斯原理提供了一种简洁而准确的描述方法，使我们能够通过波的波动性质来解释光的传播和折射现象。

这一理论不仅在光学领域有着重要的应用，也为我们理解光的传播提供了深刻的启示。

总之，惠更斯原理对于解释折射现象起着重要的作用。

通过构建次波源的方法，我们可以利用惠更斯原理来描述光线在不同介质中的传播和折射过程。

这一理论的提出为我们理解光的波动特性和折射现象提供了重要的思路，也为光学研究和应用提供了重要的理论基础。

通过深入学习和理解惠更斯原理，我们可以更好地认识光的本质和特性，为光学领域的发展和应用提供重要的理论支持。

惠更斯原理解释反射折射定律
惠更斯原理是描述波传播的一种原理，它可以用来解释光的反射和折射现象。

惠更斯原理的基本假设是，波传播时每个点上都可以看作是波源，每个波源都会发出一系列的波前（波阵面）。

波前可以看作是一系列等相位的点，它们表示了波的传播方向和速度。

在光的反射现象中，当一束光线照射到一个光滑的界面上时，按照惠更斯原理，可以认为光波是由无数个点波源组成的，这些波源在波前上振动，同时向前传播。

当波前达到界面时，每个波源都会成为新的波源，向各个方向传播新的波。

根据波动理论，波源和波的传播方向都会遵循迈克尔逊定律，即入射角等于反射角。

在光的折射现象中，当一束光线从一种介质传播到另一种介质时，惠更斯原理可以解释光线发生折射的过程。

按照惠更斯原理，光波在两种介质的交界面上的每个点可以看作是一个波源，它们向前发出新的波。

由于不同介质中光的传播速度不同，波源的振动频率保持不变，但传播速度改变，导致波前的形状发生变化。

根据波动理论，在介质边界上的波源会根据迈克尔逊定律发出新的波，使波前在新介质中以新的速度传播。

根据几何光学，根据斯涅尔定律，入射角、折射角和介质的折射率之
间满足一定的关系。

因此，惠更斯原理可以解释光的反射和折射定律，即入射角等于反射角以及根据斯涅尔定律，入射角、折射角和介质的折射率之间满足一定的关系。

惠更斯原理解释波的衍射
惠更斯原理是一种波动理论，它假定光波是由相互独立的粒子所组成的，当粒子通过介质时，粒子会受到介质中粒子的相互作用，从而使光波发生方向改变。

根据惠更斯原理，当光线从一种介质传播到另一种介质时，光线方向发生改变的原因是，光线在不同介质中的粒子相互作用不同，从而导致光线的传播方向发生改变。

惠更斯原理可以解释许多光学现象，如折射、反射、干涉和衍射等。

在反射过程中，惠更斯原理假定光线的反射是由于入射光线和反射光线在界面处发生相互作用，从而导致光线的方向发生改变。

在折射过程中，惠更斯原理假定光线从一种介质传播到另一种介质时，光线的方向发生改变是由于光线在不同介质中的粒子相互作用不同。

惠更斯原理还可以解释光的双折射现象。

光的双折射是指光线通过某些介质时，会发生两个相互垂直的折射光线。

惠更斯原理认为，这是由于介质的折射率随着光线的方向不同而发生变化，从而导致光线在通过介质时发生两个相互垂直的折射。

虽然惠更斯原理是一种有效的光学理论，但是它也有一些限制和注意事项。

首先，惠更斯原理假定光波是由相互独立的粒子所组成的，这个假定并不总是成立的。

其次，惠更斯原理不能解释光的所有现象，如光电效应和康普顿效应等。

此外，惠更斯原理也不能解释一些量子光学现象，如自发辐射和受激发射等。

总之，惠更斯原理是解释反射折射现象的一个重要原理，它假定光波是由相互独立的粒子所组成的，当光线从一种介质传播到另一种
介质时，光线的方向发生改变是由于光线在不同介质中的粒子相互作用不同。

虽然惠更斯原理不能解释所有的光学现象，但是它仍然是一个非常有用的光学理论，在许多光学现象的解释中都有广泛的应用。