平面汇交力系的平衡条件及例题

2、再利用解析法求合力的大小和方向。
RX F1X F2X 17.3 20 37.3KN RY F1Y F2Y 10 34.6 44.6KN
R
R
2 x
R
2 y
37.32 44.62 58.1KN
tan R y Rx
44.6 37.3
1.1957
α=50.1°
4.平面汇交力系平衡的解析条件
平面汇交力系平衡的充要条件是其合力为零。
解析式： R
R
2 x
R
2 y
0
即：
R x Fx 0 R y Fy 0
此式称为平面汇交力系的平衡方。若一个平
衡的汇交力系中存在两个未知力，可应用这两个独立
方程求得。
F
例 3：求图示绳子BC和BD的拉力。
解：1、绳子为柔性约束，只能承受拉力，由
CB
Fx
bx
正方向
F在坐标轴上的投影正负规定：当从力F始 端的投影a到终端b的方向与投影的正向一 致时，力的投影取正值；反之，取负值。
例题1：已知F1=100N，F2=F3=150N，F4=200N，试求各力 在在坐标轴上的投影值大小。
y
F1Y=F1sin45°=100 ×0.707=70.7N
F1
F1Y
FBD 14.14KN FBC 10KN
tan
Ry Rx
Y X
为合力R与x轴所夹的锐角， 角在哪个象限由各力在轴上
投影和正负确定。
例题2：如图所示，力F1和F2汇交于O点，已知
F1=20KN,F2=40KN,试求R的大小和方向。
Ry
y
F2y
F2
R 我们可以利用解析法 求合力的大小和方向

的力多边形是自身封闭的力多边形。 的力多边形是自身封闭的力多边形。
• 平面汇交力系平衡的充分与必要条件，也 平面汇交力系平衡的充分与必要条件，
可解析地表达为： 可解析地表达为：力系中各力在两个坐标 轴上投影的代数和分别为零。 轴上投影的代数和分别为零。
FR = ∑பைடு நூலகம்Fix + ∑ Fiy = 0 i =1 i =1
A
B
30 0
C
300
D
W
A
y
B
300
C
30 0
D
x
FCA FCB F
' T
300 300
C
W
FT
∑F
x
=0
0 ' T 0
FCB + FCA cos 30 + F cos 30 = 0
∑F
y
=0
0 ' T 0
FCA sin 30 − F sin 30 − FT = 0
FCA = 300kN
FCB = 346.4kN
n n 2 2
∑F
i =1
n
xi
=0
∑F
i =1
n
yi
=0
平面汇交力系应用举例
• 例3-2 小滑轮C铰接在三脚架ABC上，绳索 小滑轮C铰接在三脚架ABC上，绳索
绕过滑轮，一端连接在绞车上，另一端悬 挂重为W=100kN的重物。不计各构件的自 挂重为W=100kN的重物。不计各构件的自 重和滑轮的尺寸。试求AC和BC所受的力。 重和滑轮的尺寸。试求AC和BC所受的力。
§3-1-3平面汇交力系的平衡条件及应用
• 平面汇交力系平衡的充分和必要条件是： 平面汇交力系平衡的充分和必要条件是：

F R xa da bb cdc F R xF X 1F X2F X 3
F1 A
B F2 C
R D F3
x
a bdc
(b)
推广到任意多个力F1、F2、 Fn 组成的空间共
点力系，可得：
F R x F x 1 F x 2 F x 3 F x n F x
根据合力投影定理得
F R x F x 1 F x 2 F X n F x F R y F y 1 F y 2 F y 3 F y
F3 F3
cos450 ;
sin450
Fx4 Fy4
F4 cos450 F4 sin450
FRx Fx12.93N
FRy Fy11.23N
FR FR 2xFR 2y17.31N
arcFtRgyarc1t1g.3240.90 75
FRx
12.39
三、平面汇交力系平衡的充要解析条件： 力系中所有各力在任意坐标轴上投影的代数
• 性质4 力偶在任意轴上的投影等于零。
推论1：力偶可在其作用面内任意移动和转动，而不改变 物体的转动效应。
推论2：只要保持力偶矩的大小不变，转向不变，可以同 时改变组成力偶的力的大小和力偶臂的长短，而不改变它 对物体的转动效应。
因此，以后可用力偶的转向箭头来代替力偶。
F
F
=
d
d
5、力偶的三要素： (1)、力偶矩的大小。 (2)、力偶的转向。 (3)、力偶作用面的方位。
投影法的符号法则： 当由平衡方程求得某一未知力的值为负时，表
示原先假定的该力指向和实际指向相反。
解析法求解平面汇交力系平衡问题的 一般步骤:
1.选分离体，画受力图。分离体选取应最好含题设 的已知条件。

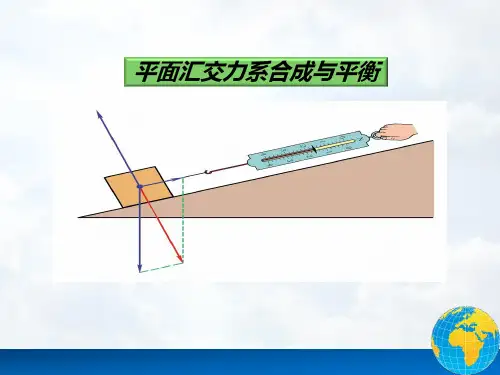
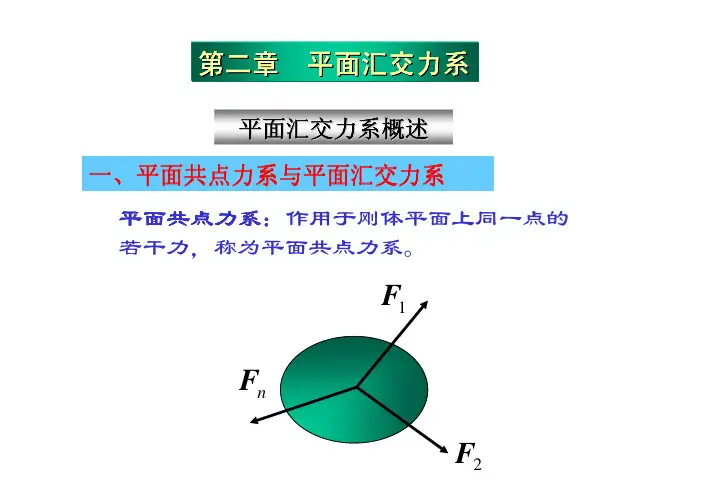
第二章平面汇交力系一、平面共点力系与平面汇交力系平面共点力系：作用于刚体平面上同一点的若干力，称为平面共点力系。

2F 平面汇交力系概述平面汇交力系：同一刚体平面内，位于不同点平面汇交力系的各力作用线汇交于同一点的力系，称为平面汇交力系。

说明：根据力的可传性，作用于刚体的平面汇交力系一定可以转化成平面共点力系，所以二者的研究方法相同。

以下不再区分，统称为平面汇交力系。

二、工程中的平面汇交力系问题举例工程中的平面汇交力系问题举例：：OAAF四、本章的研究内容分别用几何法和解析法研究平面汇交力系的合成与平衡一、平面汇交力系的合成—力的多边形法则§2-1几何法几何法（（矢量法矢量法））1）三个共点力的合成设为作用在A 点的力系},,{321F F F A1F 2F 3F RF R12F 1F 2F 3F 312R R 2112R F F F F F F +=+=321R F F F F ++=1RF 2F 3F 2）多个共点力的合成},,{21n F F F ⋯设为作用在A 点的汇交力系则该力系的合力为},,{}{21R n F F F F ⋯=∑=+++=in F F F F F ⋯21R123力多边形合力：如果一个力和一个力系等效，则此力称为该力系的合力。

说明说明：：力系的合成与力序无关∑=+++=in F F F F F ⋯21R 矢量方程为：二、平面汇交力系的平衡平衡条件1）从方程上说：2）几何平衡条件：力的多边形自行封闭R =F 123123例2-1压路碾子，自重P=20kN ，半径R =0.6m ，障碍物高h =0.08m 。

碾子中心O 处作用一水平拉力F 。

试求：（1）当水平拉力F =5 kN 时，碾子对地面及障碍物的压力；（2）欲将碾子拉过障碍物，水平拉力至少应为多大；（3）力F 沿什么方向拉动碾子最省力，此时力F 为多大。

解：（1）取碾子为研究对（2）根据力系平衡的几何条件根据力系平衡的几何条件，，作封闭的力多边形作封闭的力多边形。

平面力系-平面汇交力系的简化与平衡方程（常用版）(可以直接使用，可编辑完整版资料，欢迎下载）第2章平面力系192.1 平面汇交力系的简化与平衡方程 (19)2.2 力对点之矩合力矩定理 (24)2.3 力偶及其性质 (27)2.4 平面力偶系的合成与平衡方程 (30)2.5 平面一般力系的简化与平衡方程 (32)2.6 物体系统的平衡 (40)*附录Ⅱ：机械应用实例 (49)第2章平面力系本章主要介绍平面力系的简化与平衡问题，平面状态下物系平衡问题的解法。

按照力系中各力的作用线是否在同一平面内，可将力系分为平面力系和空间力系。

若各力作用线都在同一平面内并汇交于一点，则此力系称为平面汇交力系。

按照由特殊到一般的认识规律，我们先研究平面汇交力系的简化与平衡规律。

2.1 平面汇交力系的简化与平衡方程2.1.1 概述设刚体上作用有一个平面汇交力系F1、F2、…、F n，各力汇交于A点（图2-1a）。

根据力的可传性，可将这些力沿其作用线移到A点，从而得到一个平面共点力系（图2-1b）。

故平面汇交力系可简化为平面共点力系。

a ）b ）图2-1连续应用力的平行四边形法则，可将平面共点力系合成为一个力。

在图2-1b 中，先合成力F 1与F 2（图中未画出力平行四边形），可得力F R1，即 F R1＝F 1+ F 2；再将F R1与F 3合成为力F R2，即F R2＝F R1+ F 3；依此类推，最后可得F R ＝F 1+ F 2+…+ F n ＝∑F i （2-1）式中 F R 即是该力系的合力。

故平面汇交力系的合成结果是一个合力，合力的作用线通过汇交点，其大小和方向由力系中各力的矢量和确定。

因合力与力系等效，故平面汇交力系的平衡条件是该力系的合力为零。

2.1.2力在坐标轴上的投影过F 两端向坐标轴引垂线（图2-2）得垂足a 、b 、a'、b'。

线段ab 和a'b'分别为F 在x 轴和y轴上投影的大小，投影的正负号规定为：从a 到b （或从a'到b'）的指向与坐标轴正向相同为正，相反为负。

[因主矢等于各力的矢量和]
大小： M O mO (Fi )
主矩MO 方向： 方向规定 +
—
（转动效应） 简化中心： (与简化中心有关)
（因主矩等于各力对简化中心取矩的代数和）
2.平面任意力系的简化结果 固定端约束
=
=
固定端A处的约束力可简化为两个约束力FAx、FAy和一个 矩为ＭA的约束力偶
三、平面任意力系的简化结果分析
力偶只能使物体转动，转动效果 取决于力偶矩。
定义： 力偶矩 m F d + —
力偶的三要素： 大小、方向、作用面
⑵ 性质2 力偶对其所在平面内任一
点的矩恒等于力偶矩，而 与矩 心的位置无关，因此力偶对刚 体的效应用力偶 矩度量。
F
B Ad
x
O
F'
mO (F )mO (F')F(xd)F'x F d
两个推论：
①力偶可以在其作用面内任意移动，而不影响它对刚体的 作用效应。
②只要保持力偶矩大小和转向不变，可以任意改变力偶 中力的大小和相应力偶臂的长短，而不改变它对刚体的作用 效应。
§2-5 平面力偶系的合成与平衡
平面力偶系：作用在物体同一平面的许多力偶叫平面力偶系 一、平面力偶系的合成 设有两个力偶
即：FR F
即：平面汇交力系的 合力等于各分力的矢量和， 合力的作用线通过各力的 汇交点。
二、平面汇交力系平衡的几何条件
平面汇交力系平衡的充要条件是：
FR F 0
平面汇交力系平衡的必要与充分的几 何条件是：
力多边形自行封闭
例题2-1
已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm 的障碍物。求：在中心作用的水平力F的大小和碾子对障

FAC=
举
例
讲
解
小结：
后记：
教案
授课题目
章
第二章力的投影与平面汇交力系
授课时间
节
第三节平面汇交力系的平衡
检查签字
授课时数
2
授课方法
讲授
教学目标
掌握：
平面汇交力系的平衡
了解：
教学重点
平面汇交力系的平衡
教学难点
平面汇交力系的平衡
教学内容、方法及过程
附记
第三节平面汇交力系的平衡（掌握）80分钟
一、平面汇交力系平衡的几何条件
汇交力系平衡的几何条件:力多边形自行封闭
二、平面汇交力系平衡的平衡方程
当物体处于平衡状态时，平面汇交力系的合力FR为零，即：
举
例
讲
解
教学内容、方法及过程
附记
四个力作用于o点，设 ，求其合力（解析法）
支架由杆AB、AC构成，三处都是铰链约束。在点作用有铅垂力，用解析法分析两种情况下杆所受的力，并说明所受的力是拉力还是压力。
（1）AB杆：
为拉力
AC杆：为压力Fra bibliotek（2）AB杆（BC）： 为拉力。
举
例
讲
解
教学内容、方法及过程
附记
重物W=100N,设各杆、滑轮、钢丝绳自重不计，摩擦不计，A、B、C三处均为铰接连接。求杆件AB,AC受到的力。
以AB杆和AC杆建立直角坐标系A点位原点
Wsin 45 +FAB–Wsin 30 =0
FAB=
-Wcos 45 +FAC–Wcos 60 =0

平面汇交力系平衡的几何条件和解析条件平面汇交力系平衡是力学中的一个重要概念，它是指在平面内的多个力的作用下，使得物体保持静止或匀速直线运动的状态。

在实际应用中，平面汇交力系平衡的几何条件和解析条件是非常重要的，下面将分别进行介绍。

一、几何条件平面汇交力系平衡的几何条件是指在平面内的多个力的作用下，使得物体保持静止或匀速直线运动的状态所需要满足的几何条件。

具体来说，几何条件包括以下三个方面：1.力的合力为零在平面汇交力系平衡的情况下，所有力的合力必须为零。

这是因为如果合力不为零，物体就会发生加速度，从而失去平衡状态。

2.力的合力矩为零除了力的合力为零外，平面汇交力系平衡还需要满足力的合力矩为零。

这是因为如果合力矩不为零，物体就会发生旋转，从而失去平衡状态。

3.力的作用线交于同一点在平面汇交力系平衡的情况下，所有力的作用线必须交于同一点。

这是因为如果作用线不交于同一点，物体就会发生平移，从而失去平衡状态。

二、解析条件平面汇交力系平衡的解析条件是指在平面内的多个力的作用下，使得物体保持静止或匀速直线运动的状态所需要满足的解析条件。

具体来说，解析条件包括以下两个方面：1.力的合力在x轴和y轴上的分量为零在平面汇交力系平衡的情况下，所有力的合力在x轴和y轴上的分量必须为零。

这是因为如果合力在x轴或y轴上的分量不为零，物体就会发生加速度，从而失去平衡状态。

2.力的合力矩为零除了力的合力在x轴和y轴上的分量为零外，平面汇交力系平衡还需要满足力的合力矩为零。

这是因为如果合力矩不为零，物体就会发生旋转，从而失去平衡状态。

总之，平面汇交力系平衡的几何条件和解析条件是力学中非常重要的概念，它们为我们研究物体的平衡状态提供了重要的理论基础。

在实际应用中，我们需要根据具体情况选择合适的条件来分析和解决问题，以保证物体的平衡状态。

第二章平面汇交力系第一节平面汇交力系合成平面汇交力系的合成方法可以分为几何法与解析法，其中几何法是应用力的平行四边形法则（或力的三角形法则），用几何作图的方法，研究力系中各分力与合力的关系，从而求力系的合力；而解析法则是用列方程的方法，研究力系中各分力与合力的关系，然后求力系的合力。

下面分别介绍。

一、几何法首先回顾用几何法合成两个汇交力。

如图2—1a，设在物体上作用有汇交于O点的两个力F1和F2，根据力的平行四边形法则，可知合力R的大小和方向是以两力F1和F2为邻边的平行四边形的对角线来表示，合力R的作用点就是这两个力的汇交点O。

也可以取平行四边形的一半即利用力的三角形法则求合力如图2—1b所示。

图2—1对于由多个力组成的平面汇交力系，可以连续应用力的三角形法则进行力的合成。

设作用于物体上O点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2—2a所示。

应用力的三角形法则，首先将F1与F2合成得R1，然后把R1与F3合成得R2，最后将R2与F4合成得R，力R就是原汇交力系F1、F2、F3、F4的合力，图2—2b所示即是此汇交力系合成的几何示意，矢量关系的数学表达式为R=F1+F2+F3+F4 （2—1）实际作图时，可以不必画出图中虚线所示的中间合力R1和R2，只要按照一定的比例尺将表达各力矢的有向线段首尾相接，形成一个不封闭的多边形，如图2—2c所示。

然后再画一条从起点指向终点的矢量R，即为原汇交力系的合力，如图2—2d所示。

把由各分力和合力构成的多边形abcde称为力多边形，合力矢是力多边形的封闭边。

按照与各分力同样的比例，封闭边的长度表示合力的大小，合力的方位与封闭边的方位一致，指向则由力多边形的起点至终点，合力的作用线通过汇交点。

这种求合力矢的几何作图法称为力多边形法则。

从图2—2e还可以看出，改变各分力矢相连的先后顺序，只会影响力多边形的形状，但不会影响合成的最后结果。

图2—2将这一作法推广到由n 个力组成的平面汇交力系，可得结论：平面汇交力系合成的最终结果是一个合力，合力的大小和方向等于力系中各分力的矢量和，可由力多边形的封闭边确定，合力的作用线通过力系的汇交点。

第二章 平面汇交力系一、内容提要本章讲述了研究平面汇交力系的合成和平衡条件的两种方法：几何法和解析法。

1.求平面汇交力系的合力 (1) 几何法求合力。

根据力多边形法则求合力，即力多边形缺口的封闭边代表合力的大小和方向。

F R =ΣF合力的作用线通过原力系各力的汇交点。

(2) 解析法求合力。

根据合力投影定理，利用力系中各分力在两个正交轴上的投影的代数和，来确定合力的大小和方向为()()2Y 2X 2RY 2X R F F F F F R ∑+∑=+=XY XRY tan F F F F R ∑∑==αα为合力F R 与x 轴所夹的锐角。

合力F R 的指向由ΣF Y 和ΣF X 的正负号来确定，合力的作用线通过原力系各力的汇交点。

2.平面汇交力系的平衡条件(1) 平衡的必要和充分条件：平面汇交力系的合力为零，即F R =ΣF =0(2) 平衡的几何条件：平面汇交力系的力多边形自行封闭。

(3) 平衡的解析条件：平面汇交力系中所有各力在两个坐标轴上投影的代数和分别等于零。

即ΣF X =0 ΣF Y =0通过这两个独立的平衡方程，可求解出两个未知量。

3.力在坐标轴上的投影为F X =±F cosαF Y =±F sinα式中α为力F 与坐标轴x 所夹的锐角。

二、典型例题解析例 简易起重机如图2-1a 所示。

B 、C 为铰支座，钢丝绳的一端缠绕在卷扬机的点D 上。

杆件AB 、AC 及滑轮的自重不计，滑轮的半径也不计。

试求杆件AB 、AC 所受的力。

（空13行） 图2-1知识点：平面汇交力系的平衡条件及应用。

解 （1）取铰A 为研究对象。

杆AB 、AC 均为二力杆，可设为拉力。

由于A 处为定滑轮，故钢丝绳两端的拉力相等，都等于物体的重量W = 20kN 。

不计滑轮半径，则铰A 的受力图如图2-1b 所示。

（2）几何法求解作闭合的力多边形。

在选定比例尺后，先画已知力F T D 和W ，考虑到实际情况，F N C 应该为压力，所以应向上，且与水平成60°角。

研究方法：几何法，解析法。
各力的作用线都在同一平面内且 汇交于一点的力系。
正文
力在直角坐标轴上的投影
1
Fx=F·cosa ; Fy=F·sina = F ·cosb
说明： （1）力在坐标轴上的投影为代数量； （2）力的指向与坐标轴的正向一致时，力的投影为正值，否则为负。
正文
合力投影定理
推论1：力偶对刚体的作用与力偶在其作用面内的位置无关；
推论2：只要保持力偶矩的大小和力偶的转向不变，可以同时改变力偶中力的大小和力偶臂的长短，而不改变力偶对刚体的作用。
M
M
M
力偶表示方法
正文
思考：
力偶与力的异同
共同点：单位统一，符号规定统一。 差异点：1.力矩随矩心位置不同而变化；力 偶矩对物体作用效果与矩心选取无关。 2.力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力。
′
F
M
单 手 攻 丝
正文
平面任意力系的简化
1
平面一般力系向平面内一点简化
F3
F1
F2
O
O
O
F
R′
MO
F
1′
M1
F1 =F1
′ M1=MO(F1)
F
2′
M2
F
3′
M3
F2 =F2
′ M2=MO(F2)
F3 =F3
′ M3=MO(F3)
简化中心
O
FR=F1+F2+F3= F1+F2+F3 MO=M1+M2+M3=MO(F1)+ MO(F2) + MO(F3)
正文
平面力偶系的合成与平衡

∑ Fx = 0 B ∑ M A ( F ) = 0 A x ∑ M ( F ) = 0 B 其中A、B两点的连线AB不能垂直于投影轴x。
′ FR
由后面两式知：力系不可能简化为一力偶，只能简化 为过A、B两点的一合力或处于平衡。再加第一条件， 若AB连线不垂直于x 轴 (或y 轴），则力系必平衡。
∴N B =
60 =300N 0.2
[例4] 图示结构，已知M=800N.m，求A、C两点的约束反力。 例 图示结构，已知Байду номын сангаас， 、 两点的约束反力。 两点的约束反力
M AC = R C ⋅ d = 0.255 R C ( N .m )
∑M
i
=0
M AC − M = 0
RC = 3137 N
3 平面任意力系的平衡条件和平衡方程
M =m1 +m2 +m3 +m4 =4×(−15)=−60N⋅m
由力偶只能与力偶平衡的性质， 由力偶只能与力偶平衡的性质， 与力N 组成一力偶。 力NA与力 B组成一力偶。 根据平面力偶系平衡方程有: 根据平面力偶系平衡方程有
NB ×0.2 − m1 − m2 − m3 − m4 = 0
∴N A = N B =300 N
1,3,4；
有效的方程组合是：1,2,3；1,2,4；1,2,5；1,4,5; 2,4,5 ；2,3,5; 3,4,5
第3章 力系的平衡条件与平衡方程 章
1 平面汇交力系的平衡条件与平衡方程 2 平面力偶系的平衡条件与平衡方程 3 平面任意力系的平衡条件与平衡方程 4 简单的刚体系统平衡问题 5 考虑摩擦时的平衡问题 6 结论与讨论
1 平面汇交力系平衡的几何条件
平面汇交力系平衡的必要与充分条件是： 该力系的合力等于零。用矢量式表示为：

y
600 150 300
B B T E
300 150 0 BC 15 300
C D
x TBD=G
A
TBD
FAB
G
E
• 解题步骤： ①确定研究对象，作研究对象的受力图； ②选定坐标系； ③列平衡方程并求解。 • 指向假设的未知力，若按平衡方程求得 正值，说明其实际方向与假设的相同； 若为负值，则说明其实际方向与假设的 相反，但不需要改变受力图中的指向。
2 x 2 y 2 2
合力R的方向为： Ry 16.65 t an Rx 41.16
16.65 arctan arctan 21.79 Rx 41.16 Ry
由于 Rx ＞0， ＞0，故α在第一象 限，而合力R的作用线通过汇交力系的汇 交点。
Ry
二、平面汇交力系的平衡
TBD=G
A
TBD
FAB G
E
解：1、取滑轮连同重物E为研究对象，受力分析：
2、取汇交点B为坐标原点，建立坐标系： 3、列平衡方程并求解： X= 0 Y= 0 - TBC cos300 - TBD cos450 + FAB cos600= 0 - TBC cos600 - TBD cos450 + FAB cos300-G= 0 FAB = 45 kN TBC = 9.65 kN
如下图，在直角三角形中a为角A的对边 b为角A的邻边 c为三角形的斜边
B c a ┌ A b C
回顾与思考 1
锐角三角函数定义
正弦,余弦,
B
a sin A , c b cos A , c
b sin B , c a cos B , c
c
a
A b ┌ C

FR F1 F2 Fn Fi
i 1
n
力FR对刚体的作用与原力系对该刚体的作用等效。所以 称此力为汇交力系的合力。
如力系中各力作用线均沿同一直线，则此力系为共线力系， 它是平面汇交力系的特殊情况。显然力系的合力大小和方向 取决于各分力的代数和，即 n
FR Fi
i 1
24
静力学
例题 1-5
平面力系
合力的大小：
2 Rx 2 Ry
FR F F 171.3 N
合力与轴x，y夹角的方向余弦为：
FRx cos( FR , i ) 0.754 FR
F2
y
F1
60
O
45
30
cos( FR , j )
FRy FR
45
x
F4
0.656
F3
平面力系
Fx Fx1 Fx 2 Fxn Fxi i 1 n Fy Fy1 Fy 2 Fyn Fyi i 1
n
合力矢FR的大小和方向余弦为
FR Fx2 Fy2 ( Fxi ) 2 ( Fyi ) 2
B
D
钢丝绳的另一端绕在铰车D上。 杆AB与BC铰接，并以铰链A，C 与墙连接。如两杆与滑轮的自重
4 .由力三角形图c可得：
I
F
q
FD

J
K
FB
(c)
sin 180 q FB F 750 N sin
11
静力学
例题 1-2
平面力系
水平梁AB中点C作用着力F，其大小等于2 kN，方向与梁
的轴线成60º 角，支承情况如图a 所示，试求固定铰链支座A和活动铰链支座B的约束源自。梁的自重不计。3，

只要不平行即可
平面简单力系
平面汇交力系合成与平衡的解析法
2. 解析法解题步骤： 解析法解题步骤： （1）选取研究对象； 选取研究对象； （2）画出研究对象的受力图； 画出研究对象的受力图； （3）合理选取坐标系，列平衡方程求解； 合理选取坐标系，列平衡方程求解； （4）对结果进行必要的分析和讨论。 对结果进行必要的分析和讨论。 几点说明： 几点说明： （1）投影轴常选择与未知力垂直，最好使每个方程中只有一个 投影轴常选择与未知力垂直， 未知数； 未知数； （2）未知力的方向可以先假设，如果求出负值，说明与假设相 未知力的方向可以先假设，如果求出负值， 反。对于二力构件，一般先设为拉力，如果求出负值，说 对于二力构件，一般先设为拉力，如果求出负值， 明物体受压力。 明物体受压力。
引 言
桥梁受有：自身重力、铁轨压力、桥墩作用力、风载等。 桥梁受有：自身重力、铁轨压力、桥墩作用力、风载等。 机身受有：自身重力、旋翼轴的作用力、空气动力等。 机身受有：自身重力、旋翼轴的作用力、空气动力等。 研究内容：刚体在各种力系作用下平衡的一般规律。 研究内容：刚体在各种力系作用下平衡的一般规律。
平面简单力系
平面汇交力系合成与平衡的几何法
结论：平面汇交力系可简化为一合力，其合力的大小与方向由 结论：平面汇交力系可简化为一合力， 力多边形的封闭边来表示，其作用线通过各力的汇交点， 力多边形的封闭边来表示，其作用线通过各力的汇交点， 即合力等于各分力的矢量和（或几何和）。 即合力等于各分力的矢量和（或几何和）。 几点讨论： 几点讨论：
引 言
r r r 的质点上。 设：共点力系 {F ,F ,L,F }作用在质量为 m 的质点上。 1 2 n
i =1 r 结论： 结论：力系中 ∑F 是反映其作用效应的物理量之一 i i =1 r F

co sF R ,jF F R yF R F iy1 1 1 7 2 1 ..3 30 .6 5 5 6
A
9
• 例 如图所示，固定的圆环上作用着共面的三个力，已 知三力均通过圆心。试求此力系合力的大小和方向。
解析法 取如图所示的直角坐标系Oxy
则合力的投影分别为
RxF 1co3s0F2F3co6s04.1k6N RyF 1si3 n0F3si6 n 01.6k5N
由合力投影定理有：
Rx=X1+Xa2+c…- +Xn=X Ry=Y1+Yb2c+…=a+Ybn=Y
R
F2
F1 a b cx
合力：
合力的投影
R R x2 R y2 X 2 Y2 y
tan Ry Y
Rx
Rx X
Ry
R
x
表示合力R与 x轴所夹的锐角，
合力的指向由∑X、∑Y的符A号判定。
6
合力投影定理
i 1 4
F iy F 1 c o s 6 0 o F 2 c o s 3 0 o F 3 c o s 4 5 o F 4 c o s 4 5 o 1 1 2 .3 N
i 1
F R F x 2 F y 2( F ix )2 ( F iy )2
129.32112.32N 171.3N
co sF R ,iF F R xF R F ix1 1 2 7 9 1 ..3 30 .7 5 4 8
A
3
解析法—定量计算合力的大小和方向的方法 一、力在直角坐标轴上的投影
a a2
F
y
α b2
Fx x
a1
α、β为力与x轴和y轴所 夹的锐角， Fy
若已知力F在x、y轴上的投影

平面汇交平衡力系的充要条件平面汇交平衡力系的充要条件，听起来是不是有点让人头疼？别着急，我们慢慢来，轻松搞定！先想象一下，假如你正站在一条长长的木板上，木板两头各放着一根绳子，绳子一头拉紧了，你会怎么想？肯定是木板不动，这时候，木板上面和下面的绳子拉力应该是平衡的，对吧？不过，一旦绳子松了，木板就会倾斜，不再保持原来的平衡了。

所以，平衡力系，其实就是一个让物体保持不动或者匀速直线运动的力量系统。

它讲的就是力的分布，什么时候力的大小和方向合起来，才能让物体稳稳地待在原地不动，或者保持着匀速直线运动。

这样讲应该能明白点了吧？你得明白，平衡力系是有条件的。

不是随便哪两个力放一起就能平衡的。

举个例子，假如你和你朋友一块儿推车，车子如果能不动，那么你俩推的力大小应该差不多，而且方向得一致，才行。

换个角度说，物体的平衡，就是外力的“有序”分布。

这就好比一个团队，大家各自发挥作用，按部就班地工作，目标才能一致，任务才能顺利完成。

所以，平衡力系的充要条件就要分成两个方面来看看。

第一个条件，力要合成零。

这就是说，所有的力合在一起，不能产生任何的推动力，得让它们“相互抵消”。

这就像你俩推车的时候，如果推得差不多但不完全一样，那车就不会动，正好停在那里，这就是力的合成零。

第二个条件，所有的力矩之和也得是零。

你可以想象一下，力矩就像是一种“扭动”的效果，如果有力矩，就好像你手上拿着一根棍子，往某个方向用力，棍子就会转动。

要想让物体不转，所有的力矩必须平衡。

也就是说，不管你怎么施力，力的大小和方向得让物体不“翻转”，才能保持平衡。

再说得简单点，假如你正站在游乐场的跷跷板上，你和你的伙伴站在跷跷板两端，如果你俩的体重差不多，并且站的位置适当，跷跷板就会平衡，不动。

可是，如果你俩站得不对，或者一方站得特别近，另一方站得特别远，跷跷板就会倾斜。

这个道理其实就和平衡力系有关系。

它讲究的就是力的平衡，你怎么站，站得多远，站得多近，力矩的作用都得恰到好处，才能让跷跷板稳稳当当。