圆柱的截交线

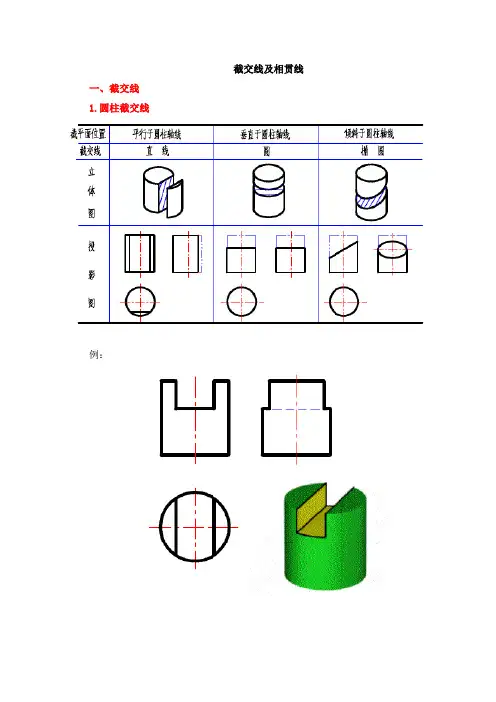
截交线及相贯线
一、截交线
1.圆柱截交线
例：
2.圆锥截交线
和圆柱的截交线一样，圆锥截交线的形状也因截平面和圆锥轴线的相对位置不同而不同，表中列出圆锥截交线的五种类型。

例：求圆锥被正垂面截切后的水平投影和侧面投影。

3.圆球的截交线
无论截平面与球的相对位置如何，截平面与球的交线均为圆。

当截面与某一投影面平行时，截交线在该投影面上的投影反映实形。

若截面倾斜于某一投影面，则截交线在该投影面上的投影为椭圆。

例：完成半圆球开槽后的正面投影和水平投影。

二、相贯线
两立体表面的交线称为相贯线。

圆柱相贯的相贯线
例：求两圆柱的相贯线
若在圆柱上开孔，即一圆柱外表面与另一圆柱内表面相交，作图方法和相贯线形状完全相同。

相贯线变化的趋势。

《圆柱的截交线》说课稿尊敬的各位评委老师好：今天我说课的课题是圆柱的截交线，下面我将从教材分析、学情分析、教法学法、过程设计、教学反思五个方面来展开本次说课。

一、教材分析（一）教材的地位和作用1、教材的地位本课题选自高教版《汽车机械制图》第三章第三节。

《汽车机械制图》是汽修专业学生必修的一门专业基础课，是学生为以后学习专业知识所必须具备的基础知识。

圆柱的截交线是本章的一个重点知识，在整个绘图知识体系中起到承上启下的作用，既承上了前面所学习的圆柱的投影的知识，又为以后组合体视图，零件图，装配图的学习奠定了基础。

（二）教学目标根据本教材的结构和内容分析，结合学生的知识基础和认知结构，我确定以下教学目标：知识目标：理解平面与圆柱轴线分别处于平行、垂直时形成的截交线的空间形状及截交线的绘制能力目标：通过本节课的学习，让学生掌握分析圆柱截交线的方法，培养学生的三维空间想象能力。

情感目标：通过教学培养学生勤动手、勤思考的良好学习习惯和分析事物的方法（三）教学的重难点本着教材和学生的实际，在吃透教材的基础上，我确定了如下的教学重难点。

重点：分析平面分别平行、垂直轴线形成的圆柱切割体的截交线。

确定重点的依据：平面分别平行、垂直轴线形成的圆柱切割体的截交线应用较多。

难点：分析平面倾斜轴线形成的圆柱切割体的截交线。

确定难点的依据：学生基础差，空间想象能力较差。

二、学情分析（一）基础能力：相对较为薄弱，而具备一定的动手能力（二）认知现状：学生初步具备了看图、绘图和空间想像力三、教法学法为了让学生掌握重点，理解难点，我采取以下教法和学法说教法1、.实物展示法激发学生的学习兴趣，活跃课堂气氛，促进学生对新知识的掌握。

2、多媒体教学法通过多媒体演示具体的实例，使问题更加的直观、清晰、形象、明了。

3、任务驱动法通过给出任务——分析任务——解决任务，提高学生的学习能力。

4、小组讨论法组织学生进行分组讨论，促使学生在学习中解决问题，培养学生的团结协作的精神。

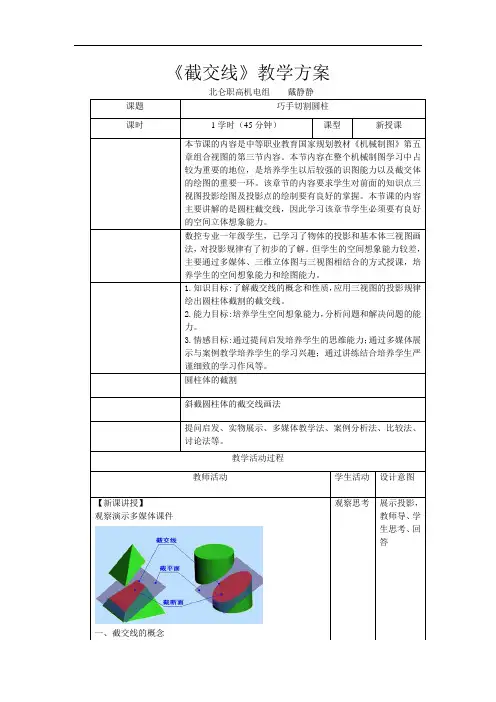
《截交线》教学方案课题巧手切割圆柱课时1学时（45分钟）课型新授课本节课的内容是中等职业教育国家规划教材《机械制图》第五章组合视图的第三节内容。

本节内容在整个机械制图学习中占较为重要的地位，是培养学生以后较强的识图能力以及截交体的绘图的重要一环。

该章节的内容要求学生对前面的知识点三视图投影绘图及投影点的绘制要有良好的掌握。

本节课的内容主要讲解的是圆柱截交线，因此学习该章节学生必须要有良好的空间立体想象能力。

数控专业一年级学生，已学习了物体的投影和基本体三视图画法，对投影规律有了初步的了解。

但学生的空间想象能力较差，主要通过多媒体、三维立体图与三视图相结合的方式授课，培养学生的空间想象能力和绘图能力。

1.知识目标:了解截交线的概念和性质，应用三视图的投影规律绘出圆柱体截割的截交线。

2.能力目标:培养学生空间想象能力，分析问题和解决问题的能力。

3.情感目标:通过提问启发培养学生的思维能力；通过多媒体展示与案例教学培养学生的学习兴趣；通过讲练结合培养学生严谨细致的学习作风等。

圆柱体的截割斜截圆柱体的截交线画法提问启发、实物展示、多媒体教学法、案例分析法、比较法、讨论法等。

教学活动过程教师活动学生活动设计意图【新课讲授】观察演示多媒体课件一、截交线的概念观察思考展示投影，教师导、学生思考、回答截交线：用平面截切几何体所形成的表面交线。

截平面：用来截切几何体的平面。

截断面：立体被截切后的断面。

二、截交线基本性质：（1）共有性。

截交线是截平面与几何体表面的共有线，截交线上的点也都是它们的共有点。

（2）封闭性。

由于几何体表面是有范围的，所以截交线一般是封闭的平面图形。

根据截交线性质，求截交线，就是求出截平面与几何体表面的一系列共有点，然后依次连接即可。

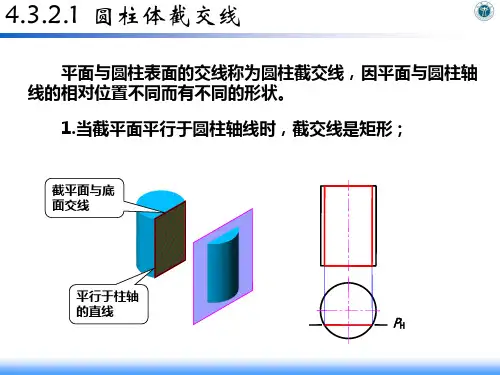
三、圆柱体的截割列出截平面与圆柱轴线相对位置不同的三种情况：1、截平面平行于轴线时，截交线的形状为矩形。

2、截平面垂直于轴线时，截交线的形状为圆。

3、截平面倾斜于平面时，截交线的形状为椭圆。