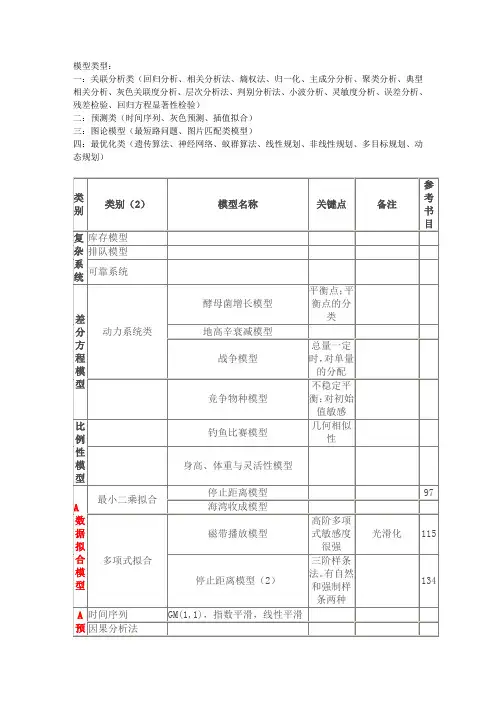
数学建模图论模型(1)
- 格式:ppt
- 大小:3.38 MB
- 文档页数:91

图论一.最短路问题问题描述:寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
将问题抽象为赋权有向图或无向图G ,边上的权均非负 对每个顶点定义两个标记(()l v ,()z v ),其中:()l v :表示从顶点到v 的一条路的权 ()z v :v 的父亲点,用以确定最短路的路线S :具有永久标号的顶点集1.1Dijkstra 算法:即在每一步改进这两个标记,使最终()l v 为最短路的权 输入:G 的带权邻接矩阵(,)w u v 步骤:(1) 赋初值:令0()0l u =,对0v u ≠,令()l v =∞,0={u }S ,0i =。
(2) 对每个(\)i i i v S S V S ∈=(即不属于上面S 集合的点),用min{(),()()}iu S l v l u w uv ∈+代替()l v ,这里()w uv 表示顶点u 和v 之间边的权值。
计算min{()}iu S l v ∈,把达到这个最小值的一个顶点记为1i u +,令11{}i i i S S u ++=⋃。
(3) 若1i V =-,则停止;若1i V <-,则用1i +代替i ,转(2)算法结束时,从0u 到各顶点v 的距离由v 的最后一次编号()l v 给出。
在v 进入i S 之前的编号()l v 叫T 标号,v 进入i S 之后的编号()l v 叫P 标号。
算法就是不断修改各顶点的T 标号,直至获得P 标号。
若在算法运行过程中,将每一顶点获得P 标号所由来的边在图上标明,则算法结束时,0u 至各顶点的最短路也在图上标示出来了。
理解:贪心算法。
选定初始点放在一个集合里,此时权值为0初始点搜索下一个相连接点,将所有相连接的点中离初始点最近的点纳入初始点所在的集合,并更新权值。
然后以新纳入的点为起点继续搜索,直到所有的点遍历。






目录五、图论模型1.迪杰斯特拉(Dijkstra)算法、贝尔曼-福特(Bellman-Ford)算法2.弗洛伊德(Floyd)算法六、分类模型1.逻辑回归2.Fisher线性判别分析五、图论模型图论模型主要解决最短路径问题,根据图的不同,对应采用迪杰斯特拉(Dijkstra)算法、贝尔曼-福特(Bellman-Ford)算法、弗洛伊德算法(Floyd)。
Matlab代码:% Matlab中的图节点要从1开始编号s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];G =graph(s,t,w);plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) set ( gca, 'XTick', [], 'YTick', [] );%% Matlab作无向图% (1)无权重(每条边的权重默认为1)% 函数graph(s,t):可在 s 和 t 中的对应节点之间创建边,并生成一个图% s 和 t 都必须具有相同的元素数;这些节点必须都是从1开始的正整数,或都是字符串元胞数组% 注意:编号从1开始连续编号s1 = [1,2,3,4];t1 = [2,3,1,1];G1 = graph(s1, t1);plot(G1)% 注意字符串元胞数组是用大括号包起来s2 = {'学校','电影院','网吧','酒店'};t2 = {'电影院','酒店','酒店','KTV'};G2 = graph(s2, t2);% 设置线的宽度plot(G2, 'line width', 2) % 画图后不显示坐标set( gca, 'XTick', [], 'YTick', [] ); % (2)有权重% 函数graph(s,t,w):可在 s 和 t 中的对应节点之间以w的权重创建边,并生成一个图s = [1,2,3,4];t = [2,3,1,1];w = [3,8,9,2];G = graph(s, t, w); plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) set( gca, 'XTick', [], 'YTick', [] ); %% Matlab作有向图% 无权图 digraph(s,t)s = [1,2,3,4, 1];t = [2,3,1,1,4];G = digraph(s, t);plot(G)set( gca, 'XTick', [], 'YTi ck', [] ); % 有权图 digraph(s,t,w)s = [1,2,3,4];t = [2,3,1,1];w = [3,8, 9,2];G = digraph(s, t, w);plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) set( gca, 'XTick', [], 'YTick', [] );1.迪杰斯特拉(Dijkstra)算法、贝尔曼-福特(Bellman-Ford)算法迪杰斯特拉算法是基于贪婪算法的思想,从起点出发逐步找到通向终点的最短距离。


11.1抗生素显著性检验问题摘要在已知抗生素效果情况服从正态分布,且方差相同条件下。
通过用SPSS13.0软件编写程序,进行单因素方差分析。
检验五种抗生素之间是否存在明显差异。
关键词:抗生素方差分析显著性检验一问题重述抗生素注入人体后会与人体血浆蛋白质结合,以致减少了药效。
现在将常用的抗生素注入到牛的体内,得到抗生素与血浆蛋白质结合的百分比。
在总体服从正态分布,且方差相同的条件下分析五种抗生素效果是否存在显著性差异。
二问题分析题目显示各类抗生素效果情况服从正态分布,为了进一步说明抗生素使用效果的差异,需要检查不同抗生素是否有显著性差异,即对数据进行显著性检验。
首先,应该提出抗生素之间没有显著性差异的假设。
然后通过SPSS13.0版本软件进行单因素方差检验[1]。
验证假设是否成立。
三模型假设四符号说明五模型建立与求解题目显示各类抗生素与血浆蛋白质结合的百分比情况属于正态总体,要对各类抗生素是否存在显著性差异。
应用软件SPSS13.0进行单因素方差检验。
其检验步骤如下:Step1. 提出假设:H:各类抗生素之间没有显著性差异;H:各类抗生素之间有显著性差异。
1α0.05。
Step2. 选定显著性水平=Step3. 用软件SPSS13.0进行单因素方差检验用SPSS13.0编写程序得到问题的解:即不同抗生素效果明显不同。
(各抗生素之间具体分析见附录一)六模型评价与改进参考文献[1]薛薇 ,《SPSS统计分析方法及应用》,出版地:电子工业出版社,2009。
[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
[编号] 作者,资源标题,网址,访问时间(年月日)。
附录附录一PSS13.0编写程序得到问题的解:11.2化肥与小麦种子的不同对小麦产量的影响问题摘要化肥与小麦的品种的差异将影响小麦的产量,进而影响农民的生活水平。
本文建立数学模型,就化肥的不同,小麦品种的不同这两种因素定量分析化肥与小麦品种对小麦实际产量的影响。
