三角函数、反三角函数整理表
- 格式:doc
- 大小:46.00 KB
- 文档页数:2

常⽤反三⾓函数公式表(完整资料).doc 此⽂档下载后即可编辑
反三⾓函数公式
arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =
2 arc tanx = cos (n arc cos x) =
反三⾓函数图像与特征
反正弦曲线图像与特征反余弦曲线图像与特征
拐点(同曲线对称中⼼):,该点切线斜率为1
拐点(同曲线对称中⼼):
,该点切线斜率为-1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中⼼):,该点切线斜率为1 拐点:
,该点切线斜率为-1
渐近线:
渐近线:
名称反正割曲线反余割曲线
⽅程
图像
顶点
渐近线
反三⾓函数的定义域与主值范围
函数主值记号定义域主值范围
反正弦若,则
反余弦若,则
反正切若,则
反余切若,则
反正割若,则
反余割若,则
式中n为任意整数.。
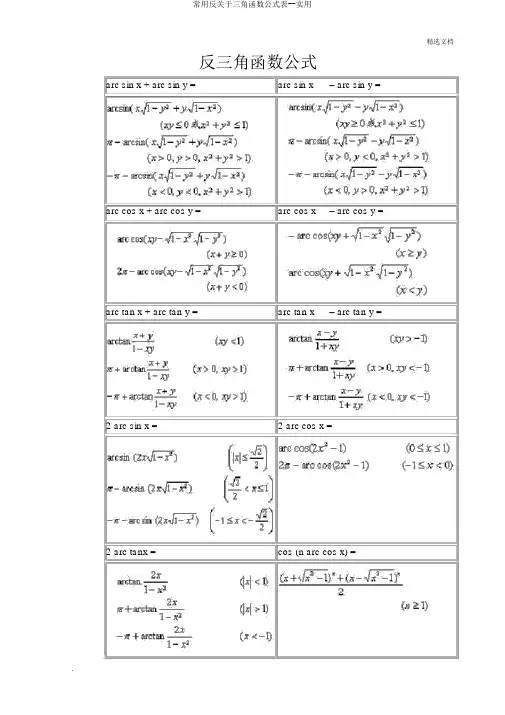
反三角函数公式arc sin x + arc sin y =arc sin x–arc sin y = arc cos x + arc cos y =arc cos x–arc cos y = arc tan x + arc tan y =arc tan x–arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx =cos (n arc cos x) =反三角函数图像与特点反正弦曲线图像与特点反余弦曲线图像与特点拐点 ( 同曲线对称中心 ) :拐点 ( 同曲线对称中心 ) :,该点切线斜率为 1,该点切线斜率为- 1 反正切曲线图像与特点反余切曲线图像与特点拐点:拐点 ( 同曲线对称中心 ) :,该点切线斜率为 1,该点切线斜率为- 1渐近线:渐近线:名称反正割曲线反余割曲线方程图像极点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若,则反余弦若,则反正切若,则反余切若,则反正割若,则反余割若,则一般反三角函数与主值的关系为式中 n 为随意整数 .反三角函数的互相关系arc sin x =arc cos x =arc tan x =arc cot x =sin x = x-x3/3!+ x5/5!-...(-1)k-1* x2k-1/(2k-1)!+... (- ∞<x<∞)cos x = 1- x2/2!+ x4/4!-...(-1)k* x2k/(2k)!+... (- ∞<x<∞)arcsin x = x + 1/2* x3/3 + 1*3/(2*4)*x5/5 + ... (| x|<1)arccos x = π- ( x + 1/2* x3/3 + 1*3/(2*4)* x5/5 + ... ) (| x|<1)arctan x = x - x^3/3 + x^5/5 - ... ( x≤1)ArcSin(x)函数功能:返回一个指定数的反正弦值,以弧度表示,返回种类为Double。

特殊三角函数值对照表(特殊角的三角函数值)《特殊角的三角函数值》是人教版数学九年级下册第二十八章的内容,特殊三角函数值一般指在0,30°,45°,60°,90°,180°角下的正余弦值。
这些角度的三角函数值是经常用到的。
并且利用两角和与差的三角函数公式,可以求出一些其他角度的三角函数值。
具体的三角函数值如下表:扩展资料:黄金三角函数介绍:α=18°(π/10) sinα=(√5-1)/4 cosα=√(10+2√5)/4tαnα=√(25-10√5)/5cscα=√5+1 secα=√(50-10√5)/5 cotα=√(5+2√5)α=36°(π/5) sinα=√(10-2√5)/4 cosα=(√5+1)/4tαnα=√(5-2√5)cscα=√(50+10√5)/5 secα=√5-1 cotα=√(25+10√5)/5α=54°(3π/10) sinα=(√5+1)/4 cosα=√(10-2√5)/4 tαnα=√(25+10√5)/5是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
扩展资料:三角函数在复数中有重要的应用。
三角函数也是物理学中的常用工具。
它有六种基本函数函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边特殊角的值如下表:在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A 的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
扩展资料:sinα = tanα × cosα(即sinα / cosα = tanα )cosα = cotα × sinα (即cosα / sinα = cotα)tanα = sinα × secα (即tanα / sinα = secα)sin ( α ± β ) = sinα · cosβ ± cosα · sinβsin ( α + β + γ ) = sinα · cosβ · cosγ +cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγcos ( α ± β ) = cosα cosβ ∓ sinβ sinαtan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ )完整初中三角函数值表如下图所示:常见的三角函数有正弦函数、余弦函数和正切函数。
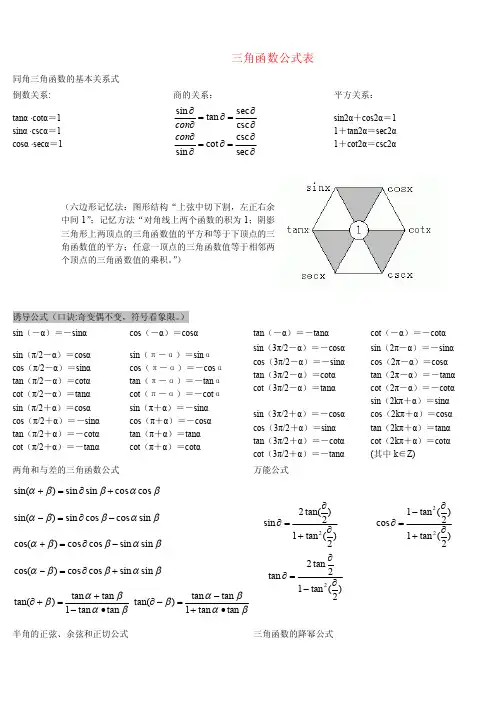

三角函数反函数特殊值表三角函数,又称为角函数,是一种常用的数学函数,也是大家最熟悉的数学函数之一。
它们主要由正弦函数,余弦函数和正切函数组成,它们的反函数也是同样的常用函数,也被称为反三角函数。
三角函数反函数是根据以下三个基本函数定义的:1.正弦函数:正弦函数定义为底角入口参数x和左闭值[-π/2,π/2]之间的正弦值y的函数,即:y=sin x。
2.余弦函数:余弦函数定义为底角入口参数x和左闭值的[-π/2,π/2]之间的余弦值y的函数,即:y=cos x。
3.正切函数:正切函数定义为底角入口参数x和左闭值的[-π/2,π/2]之间的正切值y的函数,即:y=tan x。
三角函数的反函数具有很多特殊值,这些值对于精确计算非常重要。
下表列出了三角函数反函数特殊值:【反正弦函数特殊值】xtsin xtarccos x0t0tπ/2π/6t1/2tπ/3π/4t√2/2tπ/4π/3t√3/2tπ/6π/2t1t0【反余弦函数特殊值】xtcos xtarccos x0t1t0π/6t√3/2tπ/3π/4t√2/2tπ/4π/3t1/2tπ/6π/2t0tπ/2【反正切函数特殊值】xttan xtarctan x0t0t0π/6t1/√3tπ/6π/4t1tπ/4π/3t√3tπ/3π/2t无穷大tπ/2由上可以看出,三角函数反函数具有很多特殊值,熟悉这些特殊值,对以后学习和使用三角函数反函数非常有帮助。
通常,我们使用下列公式来求解三角函数反函数:1.正弦函数: arcsin x=sin-1 x2.余弦函数: arccos x=cos-1 x3.正切函数: arctan x=tan-1 x其中,“-1”表示反函数。
另外,我们还可以使用下列公式来求解三角函数反函数:1.正弦函数: arcsin x=π/2-arccos x2.余弦函数: arccos x=π/2-arcsin x3.正切函数: arctan x=π/2-arctan (1/x)计算三角函数反函数时,可以根据以上公式和特殊值表来计算。

常用反三角函数公式表在数学的广袤领域中,反三角函数是一个重要的概念,它们在解决各种数学问题和实际应用中都发挥着关键作用。
反三角函数包括反正弦函数(arcsin)、反余弦函数(arccos)、反正切函数(arctan)等。
为了更好地理解和运用这些函数,我们需要熟悉一些常用的反三角函数公式。
一、反正弦函数(arcsin)公式1、 arcsin(x) = arcsinx这个公式表明,反正弦函数是一个奇函数,即其函数值的正负与自变量的正负相反。
2、 sin(arcsinx) = x ,其中-1 ≤x ≤ 1这是反正弦函数的定义式,意味着对一个在-1, 1范围内的数 x ,其反正弦函数的正弦值就是 x 本身。
3、 arcsinx + arcsin(x) = 0 ,其中-1 ≤ x ≤ 1这个公式进一步说明了反正弦函数的奇偶性。
二、反余弦函数(arccos)公式1、 arccos(x) =π arccosx反余弦函数不是奇函数,而是满足上述关系。
2、 cos(arccosx) = x ,其中-1 ≤ x ≤ 1与反正弦函数类似,这是反余弦函数的定义式。
3、 arccosx + arccos(x) =π ,其中-1 ≤ x ≤ 1体现了反余弦函数的特殊性质。
三、反正切函数(arctan)公式1、 arctan(x) = arctanx反正切函数是奇函数。
2、 tan(arctanx) = x ,x 为实数这是反正切函数的定义式。
3、 arctanx + arctan(1/x) =π/2 ,其中 x > 0这个公式在一些计算和证明中经常用到。
四、反三角函数的和差公式1、 arcsinx + arcsiny=arcsin(x√(1 y²) +y√(1 x²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 1 2、 arcsinx arcsiny=arcsin(x√(1 y²) y√(1 x²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 1 3、 arccosx + arccosy=arccos(xy √(1 x²)√(1 y²)),其中-1 ≤ x ≤ 1 ,-1 ≤ y ≤ 14、 arccosx arccosy= arccos(xy +√(1 x²)√(1 y²)),其中-1 ≤ x≤ 1 ,-1 ≤ y ≤ 15、 arctanx + arctany= arctan((x + y)/(1 xy)),其中xy ≠ 16、 arctanx arctany= arctan((x y)/(1 + xy)),其中xy ≠ -1五、反三角函数的倍角公式1、arcsin(2x√(1 x²))= 2arcsinx ,其中-1/√2 ≤ x ≤ 1/√22、 arccos(2x² 1) = 2arccosx ,其中0 ≤ x ≤ 13、 arctan(2x/(1 x²))= 2arctanx ,其中-1 < x < 1六、反三角函数的半角公式1、arcsin(√((1 x)/2))=(1/2)arcsinx ,其中0 ≤ x ≤ 12、arccos(√((1 + x)/2))=(1/2)arccosx ,其中-1 ≤ x ≤ 13、arctan(√((1 x)/(1 + x)))=(1/2)arctanx ,其中-1 <x < 1七、反三角函数的万能公式1、 arcsin(2tan(x/2)/(1 + tan²(x/2)))= x ,其中π/2 ≤ x ≤ π/22、 arccos((1 tan²(x/2))/(1 + tan²(x/2)))= x ,其中0 ≤ x ≤ π3、 arctan(2tan(x/2)/(1 tan²(x/2)))= x ,其中π/2 < x <π/2掌握这些常用的反三角函数公式,对于解决涉及三角函数和反三角函数的问题非常有帮助。

三角和反三角函数图像+公式
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(三角和反三角函数图像+公式)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为三角和反三角函数图像+公式的全部内容。
三角、反三角函数图像
六个三角函数值在每个象限的符号:
sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:。
反三角函数:
arcsinx arccosx
1,1])。

三角函数常用公式表格三角函数是数学中一个重要的分支,在几何、物理、工程等领域都有广泛的应用。
为了更好地理解和运用三角函数,我们需要熟悉一些常用的公式。
下面为大家整理了一份三角函数常用公式表格。
|公式名称|公式表达式|说明||||||基本关系|$\sin^2\alpha +\cos^2\alpha = 1$ |这是三角函数中最基本的关系式之一,表示正弦的平方与余弦的平方之和为1。
|||$\tan\alpha =\frac{\sin\alpha}{\cos\alpha}$|正切等于正弦除以余弦。
|||$\cot\alpha =\frac{\cos\alpha}{\sin\alpha}$|余切等于余弦除以正弦。
||诱导公式|$\sin(\pi +\alpha) =\sin\alpha$ |对于角度加上π的情况,正弦值变为其相反数。
|||$\sin(\pi \alpha) =\sin\alpha$ |角度减去π,正弦值不变。
|||$\cos(\pi +\alpha) =\cos\alpha$ |角度加上π,余弦值变为其相反数。
|||$\cos(\pi \alpha) =\cos\alpha$ |角度减去π,余弦值变为其相反数。
|||$\sin(\alpha) =\sin\alpha$ |负角度的正弦值为其相反数。
|||$\cos(\alpha) =\cos\alpha$ |负角度的余弦值不变。
||和差公式|$\sin(\alpha +\beta) =\sin\alpha\cos\beta +\cos\alpha\sin\beta$ |用于计算两个角之和的正弦值。
|||$\sin(\alpha \beta) =\sin\alpha\cos\beta \cos\alpha\sin\beta$ |计算两个角之差的正弦值。
|||$\cos(\alpha +\beta) =\cos\alpha\cos\beta \sin\alpha\sin\beta$ |两个角之和的余弦值。
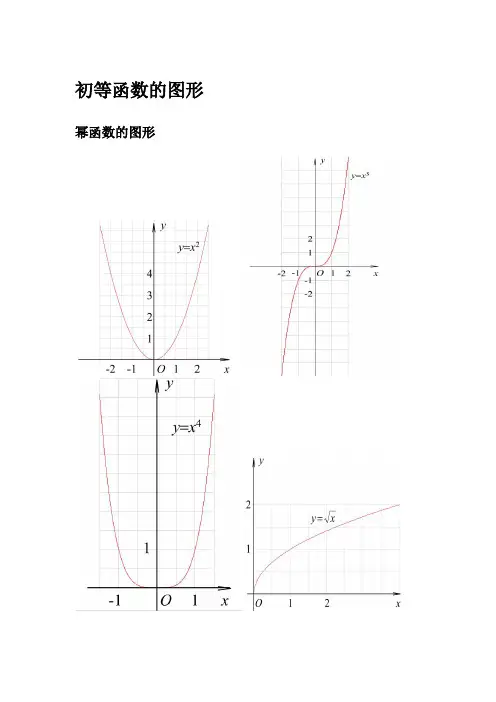
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα反三角函数的图形设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
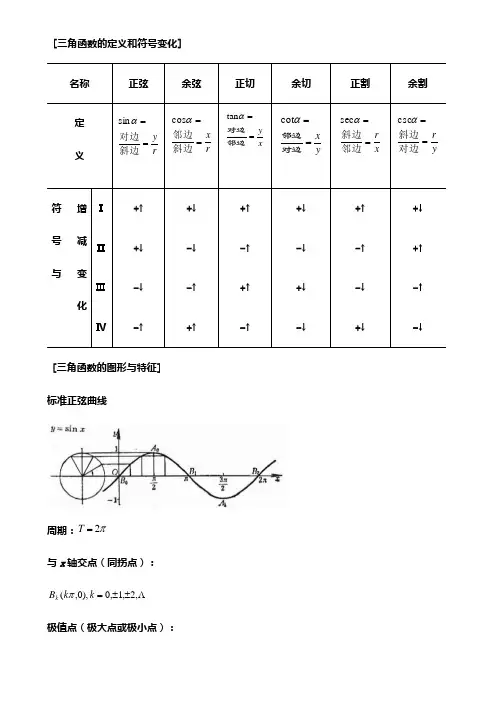
[三角函数的定义和符号变化][三角函数的图形与特征]标准正弦曲线周期:π2=T与x 轴交点(同拐点):,2,1,0),0,(±±=k k B k π极值点(极大点或极小点):,2,1,0,)1(,)21(±±=⎪⎭⎫⎝⎛-+k k A k k π余弦曲线周期:π2=T与x 轴交点(同拐点):,2,1,0,0,)21(±±=⎪⎭⎫⎝⎛+k k B k π极值点:,2,1,0),)1(,(±±=-k k A kk π 一般正弦曲线)sin(0ϕω+=x A y 周期:ωπ2=T式中A >0为振幅,ω为角频率,0ϕ为初相 与x 轴交点(同拐点):,2,1,0,0,0±±=⎪⎭⎫⎝⎛-k k B k ωϕπ 极值点:,)1(,)21(0⎪⎪⎪⎪⎭⎫ ⎝⎛--+A k A k k ωϕπ ,2,1,0±±=k同时,)cos(1ϕω+=x A y 也属于一般正弦曲线(设210πϕϕ+=,可化为))2sin(1πϕω++x A ,它是将标准正弦曲线在y 轴方向上伸长A 倍,在x 轴方向上压缩ω倍,并向左平移ωϕ0一段距离而得到.正切曲线 y =tan x周期:π=T与x 轴交点(同拐点): ,2,1,0),0,(±±=k k A k π, 该点切线斜率为1.渐近线:π)21(+=k x 余切曲线:周期:π=T与x 轴交点(同拐点):,2,1,0,0,)21(±±=⎪⎭⎫⎝⎛+k k A k π,该点切线斜率为-1.渐近线:πk x = 正割曲线周 期:π2=T 极大点:)1,)12((-+πk A k 极小点:,2,1,0),1,2(±±=k k B k π渐近线:π)21(+=k x 余割曲线周 期:π2=T极大点:⎪⎭⎫ ⎝⎛-+1,)232(πk A k 极小点:⎪⎭⎫⎝⎛+1,)212(πk B k,2,1,0±±=k渐近线:πk x =3. 特殊角的三角函数值表中02 π表示02 πϕ→,(即左、右极限).一个锐角的余角的三角函数值等于这个角的余三角函数值,例如︒=︒15sin 75cos ,︒=︒18cot 72tan ,︒=︒5.22sec 5.67csc .4. 三角函数的基本关系和公式 [诱导公式]三角函数的诱导公式表表中n 为整数. [基本关系]sin cos 221αα+=αααcos sin tan =αααsin cos cot =1cot tan =⋅αα sin csc αα⋅=1cos sec αα⋅=11tan sec 22=-αα 1cot csc 22=-αα三角函数的相互关系表例如,若sin α=x ,则cos α=±-12x[加法公式]αββαβαβαβαβαβαβαβαβαβαβαcot cot 1cot cot )cot(tan tan 1tan tan )tan(sin sin cos cos )cos(sin cos cos sin )sin(±=±±=±=±±=±[和差与积互化公式]βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαsin cos )cos(cot tan sin sin )sin(cot cot cos cos )sin(tan tan 2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos2sin sin 2cos2sin2sin sin ±=±±±=±±=±-+-=--+=+-+=--+=+sin sin [cos()cos()]cos cos [cos()cos()]sin cos [sin()sin()]αβαβαβαβαβαβαβαβαβ=-+--=++-=++-121212[倍角公式]αααααααααααααααααααααααααtan cot tan cot tan 1sec 2sec cot 21cot 2cot tan 1tan 22tan tan 1tan 1sin 211cos 2sin cos 2cos tan 1tan 2cos sin 22sin 22222222222-+=-=-=-=+-=-=-=-=+== 1cot 3cot 3cot 3cot tan 31tan tan 33tan cos 3cos 43cos sin 3sin 43sin )cot (tan 21csc sec 212csc 232333--=--=-=+-=+==ααααααααααααααααααα[半角公式]下列公式中根号所取符号与等号左边的符号一致.1sec sec 22csc 1sec sec 22sec cos 1sin sin cos 1cos 1cos 12cot cos 1sin sin cos 1cos 1cos 12tan 2cos 12cos 2cos 12sin -±=+±=-=+=-+±=+=-=+-±=+±=-±=αααααααααααααααααααααααα[降幂公式]sin (cos )sin (sin sin )sin (cos cos )sin ()cos()sin()sin()2342212012212210121214331834241212212121221αααααααααααα=-=-=-+=--+⎡⎣⎢⎤⎦⎥=--+-+=-+++=∑∑nn n k n k k n n n n nn k n kk nC n k C C n kcos (cos )cos (cos cos )cos (cos cos )cos cos()coscos()2342212012212211212143318342412221212221αααααααααααα=+=+=++=-+⎡⎣⎢⎤⎦⎥=-+-=-++=∑∑nn n k k n n n n nn k k nC n k C Cn k以上式中的n 为正整数.5. 反三角函数定义[反三角函数的定义域与主值范围]一般反三角函数与主值的关系为x n x xn x xn x n tan arc tan Arc arccos 2Arccos arcsin )1(sin Arc +=±=-+=πππ式中n 为任意整数.[反三角函数的图形与特征]反正弦曲线 反余弦曲线拐点(同曲线对称中心): 拐点(同曲线对称中心):)0,0(O ,该点切线斜率为1 )2,0(πA ,该点切线斜率为-1反正切曲线 反余切曲线拐点(同曲线对称中心): 拐点:)0,0(O ,该点切线斜率为1)2,0(πA ,该点切线斜率为-1 渐进线:2π±=y曲线对称中心:)2,0(πA 渐近线:π==y y ,0反正割曲线 反余割曲线顶点:),1(),0,1(π-B A 顶点:)2,1(),2,1(ππ--B A渐近线:2π=y渐近线:0=y6. 反三角函数的相互关系与基本公式[反三角函数的相互关系]带有*号者只当x为正值时适用. [反三角函数基本公式]7. 三角形基本定理[正弦定理]a Ab B cC R sin sin sin ===2式中R 为∆ABC 的外接圆半径(图1.3). [余弦定理]a b c bc A b c a ca B c a b ab C 222222222222=+-=+-=+-cos cos cos[勾股定理]在直角三角形(C 为直角)中,勾方加股方等于弦方(图1.4),即a b c 222+=勾股定理也称商高定理,外国书刊中称毕达哥拉斯定理.8. 斜三角形解法。
常用反三角函数公式表在数学的广阔领域中,反三角函数是一个重要的概念,它们在解决各种数学问题和实际应用中发挥着关键作用。
反三角函数包括反正弦函数(arcsinx)、反余弦函数(arccosx)、反正切函数(arctanx)等。
为了更好地理解和运用这些函数,掌握相关的公式是必不可少的。
接下来,让我们一起深入了解常用的反三角函数公式。
一、反正弦函数(arcsinx)公式1、定义域:-1, 12、值域:π/2, π/2(1)arcsin(x) = arcsinx这意味着当输入的值取相反数时,反正弦函数的值也取相反数。
(2)sin(arcsinx) = x这是一个基本的对应关系,表明对一个数先进行反正弦运算,再进行正弦运算,结果就是最初的输入值。
二、反余弦函数(arccosx)公式1、定义域:-1, 12、值域:0, π(1)arccos(x) =π arccosx与反正弦函数类似,输入值取相反数时,反余弦函数的值也有相应的变化规律。
(2)cos(arccosx) = x同样体现了先反余弦再余弦的运算结果为输入值本身。
三、反正切函数(arctanx)公式1、定义域:(∞,+∞)2、值域:(π/2, π/2)(1)arctan(x) = arctanx反映了输入值的符号变化对反正切函数值的影响。
(2)tan(arctanx) = x也是基本的对应关系。
四、反三角函数的和差公式1、 arcsinx + arcsiny=arcsin(x√(1 y²) +y√(1 x²))(|x| +|y| ≤ 1 且 xy < 0 或x²+y² ≤ 1)2、 arcsinx arcsiny=arcsin(x√(1 y²) y√(1 x²))(|x| +|y| ≤ 1 且 xy < 0 或 x²+y² ≤ 1)3、 arctanx + arctany= arctan((x + y) /(1 xy))(xy ≠ 1)4、 arctanx arctany= arctan((x y) /(1 + xy))(xy ≠ -1)五、反三角函数的复合函数公式1、 arcsin(sin x) = x (x ∈ π/2, π/2)2、 arccos(cos x) = x (x ∈ 0, π)3、 arctan(tan x) = x (x ∈(π/2, π/2))六、反三角函数的导数公式1、(arcsinx)'= 1 /√(1 x²)2、(arccosx)'=-1 /√(1 x²)3、(arctanx)'= 1 /(1 + x²)这些导数公式在微积分中非常重要,用于求解与反三角函数相关的导数问题。
(完整版)初中三角函数公式表一、三角函数的基本定义在初中数学中,三角函数主要涉及正弦函数(sin)、余弦函数(cos)和正切函数(tan)。
这些函数与直角三角形的三边长度有着密切的关系。
1. 正弦函数(sin):正弦函数表示直角三角形中,对应于一个锐角的斜边与斜边与邻边之比。
公式为:sin(θ) = 对边 / 斜边。
2. 余弦函数(cos):余弦函数表示直角三角形中,对应于一个锐角的邻边与斜边之比。
公式为:cos(θ) = 邻边 / 斜边。
3. 正切函数(tan):正切函数表示直角三角形中,对应于一个锐角的斜边与邻边之比。
公式为:tan(θ) = 对边 / 邻边。
二、三角函数的相互关系1. 正弦函数和余弦函数的关系:sin(θ) = cos(90° θ),cos(θ) = sin(90° θ)。
2. 正切函数和余弦函数的关系:tan(θ) = sin(θ) / cos(θ)。
3. 正切函数和正弦函数的关系:tan(θ) = sin(θ) / cos(θ)。
三、三角函数的特殊值1. 0°:sin(0°) = 0,cos(0°) = 1,tan(0°) = 0。
2. 30°:sin(30°) = 1/2,cos(30°) = √3/2,tan(30°) =1/√3。
3. 45°:sin(45°) = √2/2,cos(45°) = √2/2,tan(45°)= 1。
4. 60°:sin(60°) = √3/2,cos(60°) = 1/2,tan(60°) = √3。
5. 90°:sin(90°) = 1,cos(90°) = 0,tan(90°) 无定义。
四、三角函数的周期性三角函数具有周期性,即函数值在一定的周期内会重复出现。
07高中数学会考复习提纲(2)(三角函数)第四章 三角函数1、角:(1)、正角、负角、零角:逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角; (2)、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈⋅+=,360|αββ}(3)、象限的角:在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角;角的终边落在坐标轴上,这个角不属于任何象限。
2、弧度制:(1)、定义:等于半径的弧所对的圆心角叫做1(2)、度数与弧度数的换算:π= 180弧度,1弧度)180( =π(3)、弧长公式:r l ||α= (α是角的弧度数) 扇形面积:2||2121r lr S α===3、三角函数 (1)、定义:(如图) (2)、各象限的符号: yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin (3)、 特殊角的三角函数值4、同角三角函数基本关系式(1)平方关系: (2)商数关系: (3)倒数关系:1cos sin 22=+αα αααc o ss i nt a n = 1c o t t a n =αα αα22sec tan 1=+ αααs i nc o sc o t =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα(4)同角三角函数的常见变形:(活用“1”)αsinx y++ _ _ O xy++__ αcosOαtanxy+ +__O=r αsec αsinαtan αcotcsc①、αα22cos 1sin -=, αα2cos 1sin -±=;αα22sin 1cos -=, αα2sin 1cos -±=;②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=± 5、诱导公式:(奇变偶不变,符号看象限)公式一: ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k 公式二: 公式三: 公式四: 公式五:ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充:ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切)(βα+S :βαβαβαsin cos cos sin )sin(+=+ )(βα-S :βαβαβαsin cos cos sin )sin(-=- )(βα+C :βαβαβsin sin cos cos )cos(-=+a )(βα-C :βαβαβsin sin cos cos )cos(+=-a )(βα+T : βαβαβαtan tan 1tan tan )tan(-+=+ )(βα-T : βαβαβαtan tan 1tan tan )tan(+-=-)(βα+T 的整式形式为:)tan tan 1()tan(tan tan βαβαβα-⋅+=+例:若︒=+45B A ,则2)tan 1)(tan 1(=++B A .(反之不一定成立)7、辅助角公式:⎪⎪⎭⎫⎝⎛++++=+x b a b x b a a b a x b x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a(其中ϕ称为辅助角,ϕ的终边过点),(b a ,ab =ϕtan ) (多用于研究性质) 8、二倍角公式:(1)、α2S : αααcos sin 22sin = (2)、降次公式:(多用于研究性质) α2C : ααα22sin cos2cos -= ααα2sin 21cos sin =1cos 2sin2122-=-=αα 212cos 2122cos 1sin 2+-=-=ααα α2T : ααα2t a n1t a n 22t a n -= 212cos 2122cos 1cos 2+=+=ααα (3)、二倍角公式的常用变形:①、|sin |22cos 1αα=-, |cos |22cos 1αα=+;②、|sin |2cos 2121αα=-, |cos |2cos 2121αα=+③、22sin 1cos sin 21cos sin 22244ααααα-=-=+; ααα2cos sin cos 44=-;④半角:2cos 12sinαα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-= 9、三角函数的图象性质(1)、函数的周期性:①、定义:对于函数f (x ),若存在一个非零常数T ,当x 取定义域内的每一个值时,都有:f (x +T )= f (x ),那么函数f (x )叫周期函数,非零常数T 叫这个函数的周期;②、如果函数f (x )的所有周期中存在一个最小的正数,这个最小的正数叫f (x )的最小正周期。
三角函数公式综合表格整理弧度和角度之间的互相转化公式- 角度转弧度公式:$rad=\frac{π}{180}⋅deg$- 弧度转角度公式:$deg=\frac{rad⋅180}{π}$正弦函数公式- 在单位圆上,角度为 $A$ 的弦的长度为 $\sin(A)$。
- 令 $A$ 为任意角度,那么有- $\sin(A)=\sin(-A)$- $\sin(A)=\sin(A+360n)$,其中 $n$ 为任意整数- $\sin(A)=-\sin(180-A)$- $\sin(A)=\sin(A-360n)$,其中 $n$ 为任意整数- $\sin(A)=\sin(180+A)$- $\sin(180-A)=\sin(-A)$余弦函数公式- 在单位圆上,角度为 $A$ 的弦的长度为 $\cos(A)$。
- 令 $A$ 为任意角度,那么有- $\cos(A)=\cos(-A)$- $\cos(A)=\cos(A+360n)$,其中 $n$ 为任意整数- $\cos(A)=\cos(A-360n)$,其中 $n$ 为任意整数- $\cos(A)=-\cos(180-A)$- $\cos(A)=\cos(180+A)$- $\cos(180-A)=-\cos(-A)$正切函数公式- 在单位圆上,角度为 $A$ 的弦的长度为 $\tan(A)$。
- 令 $A$ 为任意角度,那么有- $\tan(A)=\tan(A+180n)$,其中 $n$ 为任意整数- $\tan(A)=\tan(A-180n)$,其中 $n$ 为任意整数- $\tan(A)=-\tan(180-A)$余切函数公式- 余切函数是正切函数的倒数,即 $\cot(A)=\frac{1}{\tan(A)}$正割函数公式- 正割函数是余弦函数的倒数,即 $\sec(A)=\frac{1}{\cos(A)}$ 余割函数公式- 余割函数是正弦函数的倒数,即 $\csc(A)=\frac{1}{\sin(A)}$以上是一些常用的三角函数公式,可以帮助你进行角度和弧度之间的转化,以及计算角度对应的正弦、余弦、正切等函数值。