福建省泉州七中2014届高三上学期第二次月考数学(理)试卷

一．选择题（共9小题）1．﹣3的相反数是（）A．﹣3B．3C．D．2．化简|﹣2|的结果是（）A．﹣2B．﹣C．D．23．某校仪仗队队员的平均身高为175cm，如果高于平均身高2cm记作+2cm，那么低于平均身高2cm应该记作（）A．2cm B．﹣2cm C．175cm D．﹣175cm4．中国的陆地面积为9598000km2，把数据9598000用科学记数法表示为（）A．9.598×107B．95.98×106C．9.598×106D．0.9598×1085．实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是（）A．a＞b B．a+b＜0C．|a|＜|b|D．a+b＞06．有以下四个结论：①绝对值等于本身的数只有正数；②相反数等于本身的数是0；③倒数等于本身的数只有1；④平方等于本身的数是0，±1．其中正确结论的个数是（）A．1B．2C．3D．47．魏晋时期数学家刘徽在《九章算术注》中用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（白色为正，黑色为负），图（1）表示的是（+23）+（﹣54）＝﹣31的计算过程，则图（2）表示的计算过程是（）A．（﹣22）+（+23）＝1B．（﹣22）+（+32）＝10C．（+22）+（﹣32）＝﹣10D．（+22）+（﹣23）＝﹣18.计算22023-（-2）2024的结果是（）A.-22023B.-1C.-2D.(-2)20249．如果x为有理数，式子2023﹣|x﹣2023|存在最大值，这个最大值是（）A．2023B．4046C．20D．010．如图，平面内有八条射线OA、OB、OC、OD、OE、OF、OG、OH，从射线OA开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7、8、9，…．按此规律，数2012在射线（）A．OA上B．OC上C．OD上D．OF上二．填空题（共4小题）11．比较大小：﹣0.5（填“＜”或“＞”或“＝”）．12．绝对值大于2而不大于4的整数有．13．已知a、b互为相反数，c、d互为倒数，则a﹣cd+b＝．14．已知有理数a、b满足（a﹣2）2+|b+1|＝0，则b a＝．15.已知a，b，c是有理数，a+b+c＝0，abc＜0，求的值．16.我们知道循环小数都可以化为分数，例如，化0.3为分数，解决方法是:设x=0.3，即x=0.333…，将方程两边都乘以10，得10x=3+0.333…，又因为x=0.333…，所以10x=3+x,即x=13，所以0.3=13.请把循环小数0.1243化为分数的结果:0.1243=____.三．解答题（共9小题）17．把下列各数分别填入相应的大括号内：﹣7，3.5，﹣3.1415，π，0，，0.03，﹣3，10，﹣0.，﹣2．自然数集合：{ …}；整数集合：{ …}；正有理数集合：{ …}；非正数集合：{ …}；有理数集合：{ …}．18．把下列各数表示在数轴上，然后把这些数按从大到小的顺序用“＞”连接起来．0，，﹣3，﹣（﹣5），，，19．计算：（1）（+7）+（﹣19）+（+23）+（﹣12）；（2）．20.（1）﹣12+5+（﹣16）﹣（﹣17）；（2）16÷|﹣8|﹣（﹣2）2×5；（3）；（4）．21．已知|a|＝3，，且a＜0，求a﹣b的值．22．出租车司机小王某天下午营运全是在南北走向的公路上进行的．如果向南记作“+”，向北记作“﹣”，他这天下午行车情况如下：（单位：千米）﹣2，+5，﹣8，﹣3，+6，﹣6．（1）小王将最后一名乘客送到目的地时，在下午出车的出发地的什么方向？距下午出车的出发地多远？（2）若出租车每公里耗油0.3升，求小王回到出发地共耗油多少升？（3）若规定每趟车的起步价是10元，且每趟车3千米以内（含3千米）只收起步价；若超过3千米，除收起步价外，超过的每千米（不足1千米按1千米计算）还需收4元钱，小王今天是收入是多少元？23．定义一种新运算：观察下列各式，并解决问题．1▽3＝1×3+3＝6，3▽1＝3×1+1＝4，5▽4＝5×4+4＝24，请你想一想：（1）4▽5＝；a▽b＝；（2）若a≠b，那么a▽b b▽a（填入“＝”或“≠”）；（3）计算：﹣5▽（﹣4▽3）．24．已知关于x的多项式（a+16）x3﹣2x22﹣b+9是二次多项式．如图1，在数轴上有A、B、C三个点，且A、B、C三点所表示的数分别是a、b、﹣21．有两条动线段PQ和MN（点Q与点A重合，点N与点B重合，且点P在点Q的左边，点M在点N的左边），PQ＝4，MN＝8，线段MN从点B开始沿数轴向左运动，同时线段PQ从点A开始沿数轴向右运动，当点Q运动到点B时，线段PQ立即以相同的速度返回，当点P运动到点C时，线段PQ、MN同时停止运动，设运动时间为t秒（整个运动过程中，线段PQ和MN保持长度不变）．（1）直接依次写出a、b的值：a＝，b＝；（2）如图2，若线段MN以每秒1个单位的速度从点B开始沿数轴向左匀速运动，同时线段PQ以每秒3个单位的速度从点A开始沿数轴向右匀速运动，当C、Q、M中任意一点为其他两点构成线段的中点时，求时间t；（3）如图3，若线段MN以每秒1个单位的速度从点B开始沿数轴向左运动，同时线段PQ以每秒3个单位的速度从点A开始沿数轴向右运动，当两条线段有重合部分时，线段PQ的速度变为原来的倍，线段MN的速度变为原来的2倍，当重合部分消失后速度恢复，请直接写出当线段PQ和MN重合部分长度为1时所对应的t的值．25．阅读下列素材：如何设计“非对称加密算法”素材1“非对称加密算法”中公钥和私钥是一对不同却匹配的钥匙，只有使用匹配的钥匙，才能完成对明文的加密解密．素材23×1001＝3003；13×1001＝13013；213×1001＝213213；……素材3项目小组正在研究利用“非对称加密算法”对1000以内的三位正整数进行加密解密，方法如下：记（公钥，私钥）为（a，b）（其中a，b均为两位正整数），则例，当明文为123，（a，b）取（13，77）时，加密解密过程如图：结合上述素材，完成以下问题：【模型理解】（1）设是一个三位数，是一个六位数，则，请说明理由．（2）设是一个三位数，是一个四位数，则被1000除的余数为请说明理由．【初步应用】（3）若公钥a为69，设计匹配的私钥b．【解决问题】（4）请再设计一对匹配的钥匙：（，）．22．请利用绝对值的性质，解决下列问题：（1）已知a，b是有理数，当a＞0时，＝；当b＜0时，＝．（2）已知a，b是有理数，且ab＜0，求的值．（3）已知a，b，c是有理数，a+b+c＝0，abc＜0，求的值．（4）已知a，b，c是有理数，当abc≠0时，求的值．一．选择题（共9小题）1．﹣3的相反数是（）A．﹣3B．3C．D．【解答】解：﹣3的相反数是﹣（﹣3）＝3．故选：B．2．化简|﹣2|的结果是（）A．﹣2B．﹣C．D．2【解答】解：根据绝对值的性质知：|﹣2|＝﹣（﹣2）＝2．故选D．3．某校仪仗队队员的平均身高为175cm，如果高于平均身高2cm记作+2cm，那么低于平均身高2cm应该记作（）A．2cm B．﹣2cm C．175cm D．﹣175cm【解答】解：由题意，高于平均身高2cm记作+2cm，高于平均身高和低于平均身高具有相反意义，所以低于平均身高2cm记作﹣2cm．故选：B．4．中国的陆地面积为9598000km2，把数据9598000用科学记数法表示为（）A．9.598×107B．95.98×106C．9.598×106D．0.9598×108【解答】解：9598000＝9.598×106．故选：C．5．实数a，b在数轴上对应的点的位置如图所示，下列结论正确的是（）A．a＞b B．a+b＜0C．|a|＜|b|D．a+b＞0【解答】解：由题可得：a＜0＜b，|a|＞|b|，∴a+b＜0，故选：B．6．有以下四个结论：①绝对值等于本身的数只有正数；②相反数等于本身的数是0；③倒数等于本身的数只有1；④平方等于本身的数是0，±1．其中正确结论的个数是（）A．1B．2C．3D．4【解答】解：①绝对值等于本身的数有正数和零，故原说法错误，不符合题意；②相反数等于本身的数是0，正确，符合题意；③倒数等于本身的数有1和﹣1，故原说法错误，不符合题意；④平方等于本身的数是0，+1，故原说法错误，不符合题意．故选：A．7．魏晋时期数学家刘徽在《九章算术注》中用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（白色为正，黑色为负），图（1）表示的是（+23）+（﹣54）＝﹣31的计算过程，则图（2）表示的计算过程是（）A．（﹣22）+（+23）＝1B．（﹣22）+（+32）＝10C．（+22）+（﹣32）＝﹣10D．（+22）+（﹣23）＝﹣1【解答】解：由题意可得：图（2）表示的计算过程是（﹣22）+（+32）＝10．故选：B．8.计算22023-（-2）2024的结果是（）A.-22023B.-1C.-2D.(-2)2024【解答】22023-(-2)2024=22023-22024=22023×(1-2)=-22023故选：A9.如果x为有理数，式子2023﹣|x﹣2023|存在最大值，这个最大值是（）A．2023B．4046C．20D．0【解答】解：∵绝对值具有非负性，∴|x﹣2023|≥0，∵2023﹣|x﹣2023|有最大值，∴当|x﹣2023|＝0时，式子有最大值，此时的值是2023，故A正确．故选：A．10．如图，平面内有八条射线OA、OB、OC、OD、OE、OF、OG、OH，从射线OA开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7、8、9，…．按此规律，数2012在射线（）A．OA上B．OC上C．OD上D．OF上【解答】解：∵平面内有公共端点的八条射线OA、OB、OC、OD、OE、OF、OG、OH，从射线OA开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7、8、9，…，∴每8个数字就回到射线OA的位置，而2012÷8＝251…4，∴数2012在射线OD上．故选：C．二．填空题（共4小题）11．比较大小：﹣0.5＞（填“＜”或“＞”或“＝”）．【解答】解：∵|﹣0.5|＝0.5，||＝，0.5＜，∴﹣0.5＞．故答案为：＞．12．绝对值大于2而不大于4的整数有﹣4，﹣3，3，4．【解答】解：绝对值大于2且不大于4的整数有﹣4，﹣3，3，4．故答案为：﹣4，﹣3，3，4．13．已知a、b互为相反数，c、d互为倒数，则a﹣cd+b＝﹣1．【解答】解：由题意，得a+b＝0，cd＝1，∴a﹣cd+b＝a+b﹣cd＝0﹣1＝﹣1．14．已知有理数a、b满足（a﹣2）2+|b+1|＝0，则b a＝1．【解答】解：由题意得，a﹣2＝0，b+1＝0，解得a＝2，b＝﹣1，所以，b a＝（﹣1）2＝1．故答案为：1．15.已知a，b，c是有理数，a+b+c＝0，abc＜0，求的值．【解答】解：∵a+b+c＝0，abc＜0，∴三个数中必需有两个正数，一个负数，可设a＞0，b＞0，c＜0∴a＝﹣（b+c），b＝﹣（a+c），c＝﹣（a+b），∴原式＝++＝﹣1﹣1+1＝﹣1；16.我们知道循环小数都可以化为分数，例如，化0.3为分数，解决方法是:设x=0.3，即x=0.333…，将方程两边都乘以，得10x=3+0.333…，又因为x=0.333…，所以10x=3+x,即x=13，所以0.3=13.请把循环小数0.1243化为分数的结果:0.1243=____.【解答】解：设x=0.1243，将方程两边都乘以10000，得10000x=1243+0.1243，所以9999x=1243，即x=113909三．解答题（共9小题）17．把下列各数分别填入相应的大括号内：﹣7，3.5，﹣3.1415，π，0，，0.03，﹣3，10，﹣0.，﹣2．自然数集合：{ 0，10…}；整数集合：{ ﹣7，0，10，﹣2…}；正有理数集合：{ 3.5，，0.03，10…}；非正数集合：{ ﹣7，﹣3.1415，0，﹣3，﹣0.，﹣2…}；有理数集合：{ ﹣7，3.5，﹣3.1415，0，，0.03，﹣3，10，﹣0.，﹣2…}．【解答】解：自然数集合：{0，10…}；整数集合：{﹣7，0，10，﹣2…}；正有理数集合：{3.5，，0.03，10…}；非正数集合：{﹣7，﹣3.1415，0，﹣3，﹣0.，﹣2…}；有理数集合：{﹣7，3.5，﹣3.1415，0，，0.03，﹣3，10，﹣0.，﹣2…}．故答案为：0，10；﹣7，0，10，﹣2；3.5，，0.03，10；﹣7，﹣3.1415，0，﹣3，﹣0.，﹣2；﹣7，3.5，﹣3.1415，0，，0.03，﹣3，10，﹣0.，﹣2．18．把下列各数表示在数轴上，然后把这些数按从大到小的顺序用“＞”连接起来．0，，﹣3，﹣（﹣5），，，【解答】解：∵＝＝1.5，﹣（﹣5）＝5，＝﹣＝﹣1.5，＝﹣＝﹣4.5，|﹣3|＝3，|﹣1.5|＝1.5，|﹣4.5|＝4.5，1.5＜3＜4.5，在数轴上表示为：∴．19．计算：（1）（+7）+（﹣19）+（+23）+（﹣12）；（2）．【解答】解：（1）（+7）+（﹣19）+（+23）+（﹣12）＝（7+23）﹣（19+12）＝30﹣31＝﹣1；（2）＝（﹣5+3）﹣（6.5+4.5+2）＝﹣2﹣13＝﹣15．20.计算（1）﹣12+5+（﹣16）﹣（﹣17）；（2）16÷|﹣8|﹣（﹣2）2×5；（3）；（4）．【解答】解：（1）原式＝﹣7﹣16+17＝﹣23+17＝﹣6；（2）原式＝16÷8﹣4×5＝2﹣20＝﹣18；（3）原式＝＝10﹣9+4＝5；（4）原式＝＝＝．21．已知|a|＝3，，且a＜0，求a﹣b的值．【解答】解：由|a|＝3，得a＝±3，∵a＜0，∴a＝﹣3，b2＝，∴b＝，∴a﹣b＝﹣3﹣＝﹣3或a﹣b＝﹣3+＝﹣2．22．出租车司机小王某天下午营运全是在南北走向的公路上进行的．如果向南记作“+”，向北记作“﹣”，他这天下午行车情况如下：（单位：千米）﹣2，+5，﹣8，﹣3，+6，﹣6．（1）小王将最后一名乘客送到目的地时，在下午出车的出发地的什么方向？距下午出车的出发地多远？（2）若出租车每公里耗油0.3升，求小王回到出发地共耗油多少升？（3）若规定每趟车的起步价是10元，且每趟车3千米以内（含3千米）只收起步价；若超过3千米，除收起步价外，超过的每千米（不足1千米按1千米计算）还需收4元钱，小王今天是收入是多少元？【解答】解：（1）﹣2+5﹣8﹣3+6﹣6＝﹣8（千米），∴小王将最后一名乘客送到目的地时，小王在下午出车的出发地的北方，距下午出车的出发地8千米．（2）|﹣2|+|5|+|﹣8|+|﹣3|+|6|+|﹣6|＝30（千米），30×0.3＝9（升），8×0.3＝2.4（升），9+2.4＝11.4（升），∴小王回到出发地共耗油11.4升．（3）根据出租车收费标准，可知小王今天的收入是10+[10+（5﹣3）×4]+[10+（8﹣3）×4]+10+[10+（6﹣3）×4]+[10+（6﹣3）×112（元），∴小王今天的收入是112元．23．定义一种新运算：观察下列各式，并解决问题．1▽3＝1×3+3＝6，3▽1＝3×1+1＝4，5▽4＝5×4+4＝24，请你想一想：（1）4▽5＝25；a▽b＝ab+b；（2）若a≠b，那么a▽b≠b▽a（填入“＝”或“≠”）；（3）计算：﹣5▽（﹣4▽3）．【解答】解：（1）4▽5＝4×5+5＝25；a▽b＝ab+b．故答案为：25；ab+b；（2）∵a▽b＝ab+b，b▽a＝ab+a，∴a▽b﹣b▽a＝（ab+b）﹣（ab+a）＝b﹣a，∵a≠b，∴b﹣a≠0∴a▽b≠b▽a．故答案为：≠；（3）﹣5▽（﹣4▽3）＝﹣5▽（﹣4×3+3）＝﹣5▽（﹣12+3）＝﹣5▽（﹣9）＝﹣5×（﹣9）+（﹣9）＝36．24．已知关于x的多项式（a+16）x3﹣2x22﹣b+9是二次多项式．如图1，在数轴上有A、B、C三个点，且A、B、C三点所表示的数分别是a、b、﹣21．有两条动线段PQ和MN（点Q与点A重合，点N与点B重合，且点P在点Q的左边，点M在点N的左边），PQ＝4，MN＝8，线段MN从点B开始沿数轴向左运动，同时线段PQ从点A开始沿数轴向右运动，当点Q运动到点B时，线段PQ立即以相同的速度返回，当点P运动到点C时，线段PQ、MN同时停止运动，设运动时间为t秒（整个运动过程中，线段PQ和MN保持长度不变）．（1）直接依次写出a、b的值：a＝﹣16，b＝20；（2）如图2，若线段MN以每秒1个单位的速度从点B开始沿数轴向左匀速运动，同时线段PQ以每秒3个单位的速度从点A开始沿数轴向右匀速运动，当C、Q、M中任意一点为其他两点构成线段的中点时，求时间t；（3）如图3，若线段MN以每秒1个单位的速度从点B开始沿数轴向左运动，同时线段PQ以每秒3个单位的速度从点A开始沿数轴向右运动，当两条线段有重合部分时，线段PQ的速度变为原来的倍，线段MN的速度变为原来的2倍，当重合部分消失后速度恢复，请直接写出当线段PQ和MN重合部分长度为1时所对应的t的值．【解答】解：（1）∵（a+16）x3﹣2x22﹣b+9是二次多项式．∴a+16＝0，22﹣b＝2，∴a＝﹣16，b＝20．故答案为：﹣16，20．（2）①当点Q未到达点B之前，Q表示的数为﹣16+3t，M表示的数为20﹣8﹣t＝12﹣t．当Q为CM中点时，CQ＝CM，如图：∴﹣16+3t﹣（﹣21）＝12﹣t﹣（﹣16+3t），∴t＝．当M为CQ中点时，CM＝MQ，如图：∴12﹣t﹣（﹣21）＝（﹣16+3t）﹣（12﹣t），∴t＝．②当点Q到达点B之后，Q表示的数为＝56﹣3t，M表示的数为20﹣8﹣t＝12﹣t．当M为CQ中点时，CM＝QM，∴12﹣t﹣（﹣21）＝56﹣3t﹣（12﹣t），∴t＝11．当t＝11时，Q从A出发，位于：﹣16+3×11＝17，未到B，故舍去．当Q为CM中点时，CQ＝MQ，如图：∴56﹣3t﹣（﹣21）＝（12﹣t）﹣（56﹣3t），∴t＝24．综上所述，时间为秒或秒或．答：时间为秒或秒或24秒．（3）当Q与M相遇时，如图：相遇时间为：[20﹣8﹣（﹣16）]÷（3+1）＝7（秒），此时，Q、M位于：﹣16+7×3＝5，∴P位于：﹣16﹣4+3×7＝1，N位于：13．当Q位于M右侧1个长度单位时，如图：时间为：1÷（3×+1×2）＝（秒），共用时：7+＝（秒）．当P位于N左侧1个长度单位时，如图：时间为：（13﹣1﹣1）÷（3×+1×2）＝（秒），共用时：7+＝（秒）．当P与N相遇时，如图：相遇时间为：（13﹣1）÷（3×+1×2）＝2（秒），共用时：7+2＝9（秒），∴P、N位于：1+3××2＝9，∴M位于：9﹣8＝1，Q位于：9+4＝13．当Q到达B时，如图：时间为：（20﹣13）÷3＝（秒），共用时：9+＝（秒），此时，N位于：9﹣1×＝，P位于：20﹣4＝16．当P追上N时，如图：时间为：（16﹣）÷（3﹣1）＝（秒），共用时：＝16（秒），此时，P、N位于：16﹣×3＝2，M位于：﹣6，Q位于：6．当P位于N左侧1个长度单位时，如图：1÷（3×﹣1×2）＝（秒），共用时：16+＝（秒）．当M位于Q左侧1个长度单位时，如图：时间为：[6﹣（﹣6）﹣1]÷（3×﹣1×2）＝（秒），共用时：＝（秒）．综上所述，时间t为：秒秒或秒或秒．答：时间为秒秒或秒或秒．25．阅读下列素材：如何设计“非对称加密算法”素材1“非对称加密算法”中公钥和私钥是一对不同却匹配的钥匙，只有使用匹配的钥匙，才能完成对明文的加密解密．素材23×1001＝3003；13×1001＝13013；213×1001＝213213；……素材3项目小组正在研究利用“非对称加密算法”对1000以内的三位正整数进行加密解密，方法如下：记（公钥，私钥）为（a，b）（其中a，b均为两位正整数），则例，当明文为123，（a，b）取（13，77）时，加密解密过程如图：结合上述素材，完成以下问题：【模型理解】（1）设是一个三位数，是一个六位数，则，请说明理由．（2）设是一个三位数，是一个四位数，则被1000除的余数为请说明理由．【初步应用】（3）若公钥a为69，设计匹配的私钥b．【解决问题】（4）请再设计一对匹配的钥匙：（11，99（答案不唯一））．【解答】解：（1）∵13×77＝1001，∴＝＝＝＝，∴；（2）∵＝＝，∵能被1000整除，∴被1000除的余数为，即被1000除的余数为．（3）∵，∴对于匹配的钥匙（a，b），则有ab＝，当公钥a为69，则匹配的私钥b＝；∵b为两位整数，∴当n＝2时，b＝＝29；（4）∵，∴对于匹配的钥匙（a，b），则有ab＝1001，∵11×91＝1001，∴匹配的钥匙（11，99）．故答案为：（11，99）（答案不唯一）．。

（山东省德州市2019届高三期末联考数学（理科）试题）8.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础设计的，会标是四个全等的直角三角形与一个小正方形拼成的一个大正方形，如果小正方形的面积为，大正方形的面积为，直角三角形中较小的锐角为，则（）A. B. C. D.【答案】D【解析】【分析】由图形可知三角形的直角边长度差为a，面积为6，列方程组求出直角边得出sinθ，代入所求即可得出答案．【详解】由题意可知小正方形的边长为a，大正方形边长为5a，直角三角形的面积为6，设直角三角形的直角边分别为x，y且x＜y，则由对称性可得y＝x+a，∴直角三角形的面积为S xy＝6，联立方程组可得x＝3a，y＝4a，∴sinθ，tanθ＝．∴===，故选：D．【点睛】本题考查了解直角三角形，三角恒等变换，属于基础题．（山东省潍坊市2019届高三上学期期末测试数学（理科）试题）3.若，则（）A. B. C. D.【答案】C【解析】【分析】本道题化简式子,计算出,结合,即可.【详解】,得到,所以,故选C.【点睛】本道题考查了二倍角公式,难度较小.（山东省烟台市2018届高三下学期高考诊断性测试数学（文）试题）14.已知,则_______【答案】【解析】原式化为，，所以，，填。

（江西省新余市2019届高三上学期期末考试数学（理）试题）15.已知，则______．【答案】【解析】【分析】根据同角的三角函数的关系和二倍角公式即可求出．【详解】解：，，，，，故答案为：．【点睛】本题考查同角的三角函数关系式和二倍角公式的应用，属于基础题．（湖南省长沙市2019届上学期高三统一检测理科数学试题）15.在平面直角坐标系中，角的顶点在原点，始边与轴的非负半轴重合，终边过点，则__________.【答案】【解析】【分析】结合终边过点坐标，计算出，结合二倍角公式和余弦两角和公式，即可。

【详解】，所以【点睛】本道题考查了二倍角公式与余弦的两角和公式，难度中等。

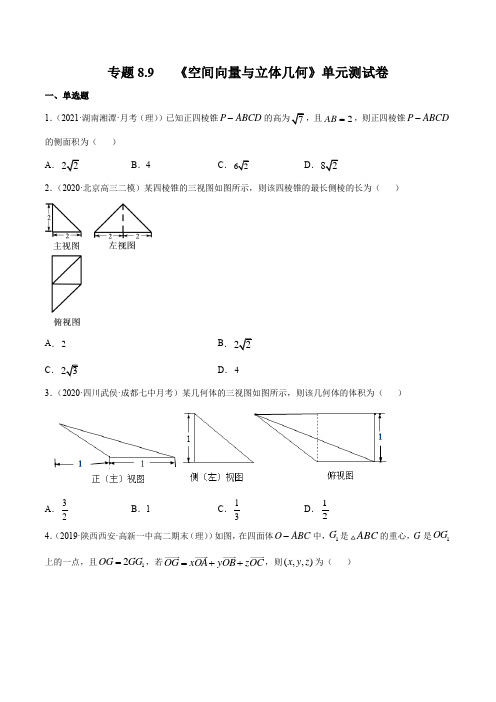
专题8.9 《空间向量与立体几何》单元测试卷一、单选题1．（2021·湖南湘潭·月考（理））已知正四棱锥P ABCD -2AB =，则正四棱锥P ABCD -的侧面积为（ ）A ．B ．4C ．D ．2．（2020·北京高三二模）某四棱锥的三视图如图所示，则该四棱锥的最长侧棱的长为（ ）A ．2B ．C ．D ．43．（2020·四川武侯·成都七中月考）某几何体的三视图如图所示，则该几何体的体积为（ ）A ．32B ．1C ．13D ．124．（2019·陕西西安·高新一中高二期末（理））如图，在四面体O ABC -中，1G 是ABC 的重心，G 是1OG 上的一点，且12OG GG =，若OG xOA yOB zOC =++，则(,,)x y z 为（ ）A ．111(, , )222B ．222(,, )333 C ．111(, , )333 D ．222(, , )999 5．（2020·云南高三月考（理））如图所示，在正方体1111ABCD A BC D -中，点E 为线段AB 的中点，点F 在线段AD 上移动，异面直线1BC 与EF 所成角最小时，其余弦值为（ ）A ．0B ．12CD ．11166．（2020·河北正定中学高三月考）已知平面α，β，γ和直线l ，下列命题中错误的是（ ） A ．若αβ⊥，//βγ，则αγ⊥B ．若αβ⊥，则存在l α⊂，使得//l βC ．若a γ⊥，βγ⊥，l αβ=，则l γ⊥D ．若αβ⊥，//l α，则l β⊥7．（2020·山东济宁·高二月考）在正方体1111ABCD A BC D -中，棱AB ，11A D 的中点分别为E ，F ，则直线EF 与平面11AA D D 所成角的正弦值为（ ）A B C D 8．（2020·山东济宁·高二月考）如图，在棱长为2的正方体1111ABCD A BC D -中，E 为BC 的中点，点P 在底面ABCD 上（包括边界．．．．）移动，且满足11B P D E ⊥，则线段1B P 的长度的最大值为（ ）A．B．C．D．359．（2020·福建省泉州第一中学月考）如图，已知正方体ABCD-A1B1C1D1棱长为8，点H在棱AA1上，且HA1＝2，在侧面BCC1B1内作边长为2的正方形EFGC1，P是侧面BCC1B1内一动点，且点P到平面CDD1C1HP的最小值是（）距离等于线段PF的长，则当点P在侧面BCC1B1运动时，2A．87B．88C．89D．9010．（2020·广西柳州·二模（理））如图所示，在直角梯形BCEF中，∠CBF=∠BCE=90°，A，D分别是BF，CE上的点，AD∥BC，且AB=DE=2BC=2AF（如图1），将四边形ADEF沿AD折起，连结BE、BF、CE（如图2）．在折起的过程中，下列说法中正确的个数（）①AC∥平面BEF；②B、C、E、F四点可能共面；③若EF⊥CF，则平面ADEF⊥平面ABCD；④平面BCE与平面BEF可能垂直A．0B．1C．2D．3二、多选题11．（2020·山东曲阜一中）在正方体1111ABCD A BC D -中，若E 为11AC 的中点，则与直线CE 不垂直的有（ ）A ．ACB ．BDC ．1AD D ．1A A12．（2020·山东曲阜一中）如图，已知E 是棱长为2的正方体1111ABCD A BC D -的棱BC 的中点，F 是棱1BB 的中点，设点D 到面1AED 的距离为d ，直线DE 与面1AED 所成的角为θ，面1AED 与面AED 的夹角为α，则（ ）A ．DF ⊥面1AEDB ．43d =C ．45sin 15θ=D ．2cos 3α= 13．（2020·历下·山东师范大学附中高二月考）下列命题中不正确的是（ ）A ．a b a b -=+是,a b 共线的充要条件B ．若,C ABD 共线，则//AB CDC ．,,A B C 三点不共线，对空间任意一点O ，若311488OP OA OB OC =++，则,,,P A B C 四点共面 D ．若,,,P A B C 为空间四点，且有PA PB PC λμ=+(,PB PC 不共线)，则1λμ+=是,,A B C 三点共线的充分不必要条件14．（2020·南京市第十四中学高二月考）如图，在直三棱柱111ABC A B C -中，12AC BC AA ===，90ACB ∠=︒，D ，E ，F 分别为AC ，1AA ，AB 的中点．则下列结论正确的是（ ）A ．1AC 与EF 相交B ．11//BC 平面DEFC ．EF 与1AC 所成的角为90︒D ．点1B 到平面DEF 的距离为2三、填空题 15．（2020·山东曲阜一中）已知向量1e ，2e ，3e 是三个不共面的非零向量，且1232a e e e =-+，12342b e e e =-+-，123115c e e e λ=++，若向量a ，b ，c 共面，则λ=________.16．（2020·扬州大学附属中学东部分校高三月考）在长方体1111ABCD A BC D -中，11,AB BC AA ===则异面直线1AD 与1DB 所成角的余弦值为__________.17．（2020·江苏省梅村高级中学高三开学考试）二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知4AB =，6AC =，8BD =，CD =，则该二面角的大小为________．18．（2020·全国高二课时练习）已知()3211a λ=-，，，()102b μμ=+，，．若a b ⊥，则μ＝_____；若//a b ，则λ+μ＝_____．19．（2020·福建省泉州第一中学月考）在长方体ABCD -A ’B ’C ’D ’中，AB ＝AA ’＝2AD ＝2，以D 为原点，DA ，DC ，'DD 方向分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，则'AC =_______，若点P 为线段AB 的中点，则P 到平面A ’BC ’距离为___________20．（2020·福建省泰宁第一中学月考）如图，在正四棱1111ABCD A BC D -中，底面边长为2，1CC =4，直线1A B 与1AD 所成角的余弦值为______.直线1CC 与平面1ACD 所成角的正弦值为 ______.21．（2020·山东潍坊·高三月考）正方体1111ABCD A BC D -的棱长为1，E ，F 分别为BC ，1CC 的中点．则平面AEF 截正方体所得的截面面积为______；以点E 11ACC A 的交线长为______．四、解答题22．（2020·历下·山东师范大学附中高二月考）如图，已知1111ABCD A BC D -是四棱柱，底面ABCD 是正方形，132AA AB ==，，且1160C CB C CD ︒∠=∠=，设1,,CD C a b B CC c ===.（1）试用,,a b c 表示1AC ； （2）已知O 为对角线1AC 的中点，求CO 的长.23．（2020·历下·山东师范大学附中高二月考）如图，在直三棱柱111ABC A B C -中，2ABC π∠=，D 是棱AC 的中点，且11AB BC BB ===.（1）求证： 1//AB 平面1BC D ；（2）求直线1AB 到平面1BC D 的距离.24．（2020·江苏鼓楼·南京师大附中高三月考）如图所示，在多面体ABCDFE 中，四边形ABEF 为正方形，平面ABEF ⊥平面,CDFE CD ∥,90,22EF CDF DFE EF CD ∠=∠=︒==.（1）若1DF =，证明：平面ACF ⊥平面BCE ；（2）若二面角A BC E --的余弦值为，求DF 的长. 25．（2020·宁夏高三其他（理））如图，在四棱柱1111ABCD A BC D -中，1AA ⊥平面ABCD ，底面ABCD满足AD ∥BC ，且12AB AD AA BD DC =====，(Ⅰ)求证:AB ⊥平面11ADD A ;(Ⅱ)求直线AB 与平面11B CD 所成角的正弦值.26．（2020·河南高三其他（理））如图，在三棱锥P ABC -中，底面是正三角形，24AB PA ==，PA ⊥底面ABC ，点E ，F 分别为AC ，PC 的中点.（1）求证：平面BEF ⊥平面P AC ；（2）在线段PB （不含端点）上是否存在点G ，使得平面EFG 与平面PBC 若存在，确定点G 的位置；若不存在，请说明理由.27．（2020·历下·山东师范大学附中高二月考）如图（1）所示，在Rt ABC 中，90︒∠=C ，3,6BC AC ==，,D E 分别是,AC AB 上的点，且//,2DE BC DE =，将ADE 沿DE 折起到1A DE △的位置，使1AC CD ⊥，如图（2）所示.（1）求证：1AC ⊥平面BCDE ；（2）若M 是1A D 的中点，求CM 与平面1A BE 所成角的大小；（3）线段BC （不包括端点）上是否存在点P ，使平面1A DP 与平面1A BE 垂直？说明理由.。

2024-2025学年福建省泉州市永春一中七年级（上）月考数学试卷（10月份）一、选择题：本题共10小题，每小题4分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.2024的相反数是( )A. 2024B. −2024C. 12024D. −120242.2024年2月29日，国家统计局发布关于《2023年国民经济和社会发展统计公报》，2023年我国国内生产总值(GDP)达126万亿元，再次跃上新台阶.其中126万亿用科学记数法表示为( )A. 1.26×1012B. 12.6×1013C. 1.26×1014D. 0.126×10153.比−1小2的数是( )A. −3B. −1C. 1D. 24.如图，数轴上的点A 、B 分别对应实数a 、b ，下列结论中正确的是( )A. a +b <0B. −a +b <0C. a−b <0D. −a−b >05.关于a +b =0，用文字语言可以描述为( )A. a ，b 互为倒数B. a ，b 互为负倒数C. a 是b 的绝对值D. a ，b 互为相反数6.把7−(−3)+(−5)−(+2)写成省略加号和的形式为( )A. 7+3−5−2B. 7−3−5−2C. 7+3+5−2D. 7+3−5+27.1m 长的小棒，第一次截去一半，第二次截去剩下的一半，如此下去，第六次后剩下的小棒长( )A. 112mB. 132mC. 164mD. 1128m8.在数轴上，一个点从−4开始，先向右移动2个单位长度，再向左移动3个单位长度后到达终点，这个终点表示的数是( )A. −1B. 1C. 5D. −59.定义关于有理数a ，b 的新运算：f(a ×b)=f(a)−f(b)，其中a ，b 为整数，a ≤b.例如：若f(3)=5，f(5)=4，则f(15)=f(3×5)=f(3)−f(5)=5−4=1.若f(4)=1，则f(64)的结果为( )A. 1B. −1C. 3D. −310.有理数a ，b ，c 满足abc ≠0，a <b 且a +b <0，|a|a +|b|b +|c|c =−1，那么|ab|ab +|bc|bc +|ac|ac +|abc|abc 的值为( )A. 0B. 2C. 0或2D. 0或−2二、填空题：本题共6小题，每小题4分，共24分。

（山东省德州市2019届高三期末联考数学（理科）试题）4.已知数列为等差数列，且成等比数列，则的前6项的和为（）A. 15B.C. 6D. 3【答案】C【解析】【分析】利用成等比数列,得到方程2a1+5d＝2，将其整体代入 {a n}前6项的和公式中即可求出结果．【详解】∵数列为等差数列，且成等比数列，∴，1，成等差数列，∴2，∴2＝a1+a1+5d，解得2a1+5d＝2，∴{a n}前6项的和为2a1+5d）=．故选：C．【点睛】本题考查等差数列前n项和的求法，是基础题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．（福建省宁德市2019届高三第一学期期末质量检测数学理科试题）3.等差数列中，，，则数列的前20项和等于（）A. -10B. -20C. 10D. 20【答案】D【解析】【分析】本道题结合等差数列性质，计算公差，然后求和，即可。

【详解】，解得，所以，故选D。

【点睛】本道题考查了等差数列的性质，难度中等。

（江西省新余市2019届高三上学期期末考试数学（理）试题）5.在等差数列中，已知是函数的两个零点，则的前10项和等于( )A. -18B. 9C. 18D. 20【答案】D【解析】【分析】由韦达定理得，从而的前10项和，由此能求出结果.【详解】等差数列中，是函数的两个零点，，的前10项和.故选：D.【点睛】本题考查等差数列的前n项和公式，是基础题，解题时要认真审题，注意等差数列的性质的合理运用.（湖南省长沙市2019届上学期高三统一检测理科数学试题）13.设等差数列的前项和为，且,则__________．【答案】【解析】分析：设等差数列{a n}的公差为d，由S13=52，可得13a1+d=52，化简再利用通项公式代入a4+a8+a9，即可得出．详解：设等差数列{a n}的公差为d，∵S13=52，∴13a1+d=52，化为：a1+6d=4．则a4+a8+a9=3a1+18d=3（a1+6d）=3×4=12．故填12.点睛：本题主要考查等差数列通项和前n项和，意在考查学生等差数列基础知识的掌握能力和基本的运算能力.（湖南省湘潭市2019届高三上学期第一次模拟检测数学（文）试题）3.已知数列是等比数列，其前项和为，，则（）A. B. C. 2 D. 4【答案】A【解析】【分析】由题意，根据等比数列的通项公式和求和公式，求的公比，进而可求解，得到答案。

福建省泉州七中2014届高三质检理科数学试题（一）参考公式：样本数据1x 、2x 、…、n x的标准差：s 中x 为样本平均数；柱体体积公式：V Sh =，其中S 为底面面积，h 为高；锥体体积公式：13V Sh =，其中S 为底面面积，h 为高；球的表面积、体积公式：24S R π=，343V R π=，其中R 为球的半径．独立性检验临界值表()20P K x ≥0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.0010x0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828第Ⅰ卷（选择题 共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．下面是关于复数21z i =-+的四个命题：其中的真命题为（ ）1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-A. 23,p pB. 12,p pC. 24,p pD. 34,p p2.如图所示的程序框图，若输出的S 是30，则①可以为（ ）A ．2?n ≤B ．3?n ≤C ．4?n ≤D ．5?n ≤3．若变量y x ,满足约束条件2010330x y x y x y -+≥⎧⎪+-≥⎨⎪--≥⎩，则实数2z x y =+ ( )A.有最小值，有最大值B. 有最小值，无最大值C.无最小值，有最大值 D .无最小值，无最大值4．为了了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机选取了60名高中生，()2第题则由以上数据，根据临界值表，以下说法正确的是（ ）A ．没有充足的理由认为课外阅读量大与作文成绩优秀有关 B. 有0.5%的把握认为课外阅读量大与作文成绩优秀有关C ．有99.9%的把握认为课外阅读量大与作文成绩优秀有关D ．有99.5%的把握认为课外阅读量大与作文成绩优秀有关5.等比数列{}n a 的各项均为正数，且564718a a a a +=， 则1012333log log log a a a +++=（ ）A. 12B. 10C. 31og 5+D. 32og 5+6.已知()24f x x x =++-的最小值为n ， 则2()n x x-的展开式中常数项为（ ）A. 160-B. 20- C . 20 D. 160 7.已知正方体1111ABCD A B C D -中，线段11B A ，11B C 上（不包括端点）各有一点P ，Q ，且11B P B Q =，下列说法中，不正确的是（ ）A. A 、C 、P 、Q 四点共面；B. 直线PQ 与平面11BCC B 所成的角为定值；C.32PAC ππ<∠<； D.设二面角P AC B --的大小为θ，则tan θ的最小8.已知点()1,0A ,若曲线Γ上存在四个点B ,C ,D ,E ,使得ABC ∆和ADE ∆都是正三角形，则称曲线Γ为“黄金曲线”，给定下列四条曲线：①2430x y +=；②2214x y +=；③2212x y +=；④2213x y -=。

2024学年安徽省A10高三语文上学期11月考试卷（满分150分，考试时间150分钟）2024.11一、现代文阅读(35分)(一)现代文阅读I(本题共5小题，19分)阅读下面的文字、完成1~5题。

材料一：对于《清明上河图》中所描绘的虹桥(图1),桥梁专家唐寰澄先生将之称为“贯木拱”桥，因其桥拱的主要部分由两套拱骨系统组成(图2),第一套木拱拱骨为三根长木，做梯形布置，另一套木拱拱骨为长木两根、短木两根，做尖拱关布置。

两套系统互相错开并排搭设，各套系统以端头抵紧，两套系统结合，形成稳定的木拱结构。

虹桥以其优美的艺术造型入选成为《清明上河图》主题表现的中心部分。

它以薄薄的拱体，使一座偌大的木桥显得轻盈苗条。

桥头培土压拱，形成了桥面平缓的反向曲线，使桥身波浪起伏，倍增观瞻。

桥端两侧矗立华表木柱，配以精致敦实的石台岸，衬托着圆弧形的拱身，突出了整个建筑立面。

桥檐封以飞边，犹如拔上了鲜明的裙带；横骨端部的戏水兽面板点缀着桥的正面，给人以朴实、端庄的印象。

桥前的华表，顶端白鹤伫立，神态各异，栩栩如生。

关于华表白鹤，杜甫诗有“裹震不涉往来通，天寒白鹤归华表”之句。

桥身“饰以丹艧”,丹艧属赤石脂类，朱色，为油漆颜料。

丹艧刷饰，是昔时营造建筑惯用的重要防腐术，又是作为装饰的一项传统手法。

宋代梁洽《梓材赋》有“上栋下宇资丹腹之余饰”之词，部昂《前题》也有“明其章于木，必须其丹漆”的句子。

虹桥的实例，表明了我国这项传统技术措施，不仅适用于静载的营造建筑，而且在经受活载的敞露于大气的桥工建筑中同样有成效。

飞边封檐和兽面横板，全有防止雨水浸蚀拱身的效用。

涂饰的漆料，受桥面蔽荫，故能长期发挥其防腐作用。

虹桥的艺术处理，体现了实用与美观的巧妙结合，达到了完美和统一，体现了昔时建筑工匠深湛的艺术造诣和认真的求实精神。

(摘编自王英钦《汴水虹桥营建技艺探究》等)材料二：宋代张择端的旷世名画《清明上河图》中的“汴水虹桥”,在中国桥梁史中因其高超的技艺和巧妙的结构而声名显赫。