锐角三角函数的计算 -

锐角三角函数公式值
锐角三角函数公式值指的是在直角三角形中，对于一个角度小于90度的锐角，其正弦、余弦、正切、余切、正割、余割的数值，可以通过特定的公式进行计算得出。

具体公式如下：
正弦(sin): sinθ=对边/斜边
余弦(cos): cosθ=邻边/斜边
正切(tan): tanθ=对边/邻边
余切(cot): cotθ=邻边/对边
正割(sec): secθ=斜边/邻边
余割(csc): cscθ=斜边/对边
其中，对边、邻边、斜边分别指直角三角形中的三条边，对边指与角度相对的边，邻边指与角度相邻的边，斜边指直角三角形的斜边。

需要注意的是，上述公式中的角度单位为弧度制。

如果给出的角度是度数，则需要先将其转化为弧度制，即弧度=角度×π/180。

- 1 -。

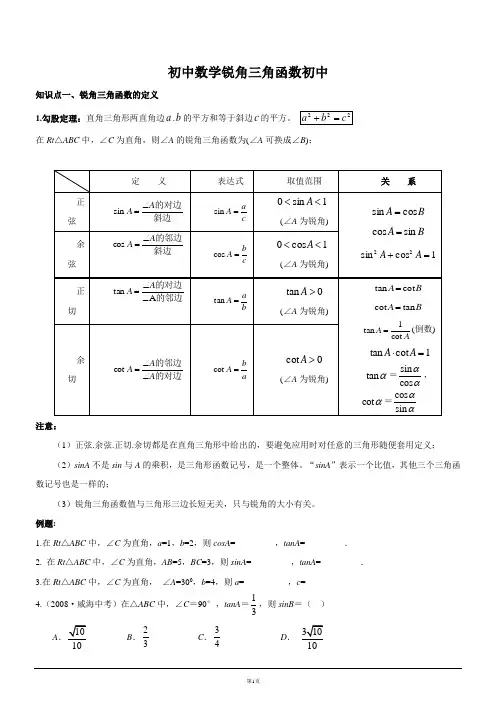
初中数学锐角三角函数初中知识点一、锐角三角函数的定义1.勾股定理：直角三角形两直角边a .b 的平方和等于斜边c 的平方。

222c b a =+ 在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B )：定 义表达式 取值范围 关 系正弦 斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=coscbA =cos1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A Aba A =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A Atan α＝sin cos αα，cot α＝cos sin αα余切的对边的邻边A A A ∠∠=cotab A =cot 0cot >A(∠A 为锐角)注意：（1）正弦.余弦.正切.余切都是在直角三角形中给出的，要避免应用时对任意的三角形随便套用定义；（2）sinA 不是sin 与A 的乘积，是三角形函数记号，是一个整体。

“sinA ”表示一个比值，其他三个三角函数记号也是一样的；（3）锐角三角函数值与三角形三边长短无关，只与锐角的大小有关。

例题:1.在Rt △ABC 中，∠C 为直角，a =1，b =2，则cosA =________ ，tanA =_________．2. 在Rt △ABC 中，∠C 为直角，AB =5，BC =3，则sinA =________ ，tanA =_________．3.在Rt △ABC 中，∠C 为直角， ∠A =300，b =4，则a =__________，c =__________4.（2008·威海中考）在△ABC 中，∠C ＝90°，tanA ＝31，则sinB ＝（ ） A ．1010B ．23 C ．34D ．310105.在△ABC 中，∠C =90°，a, b, c 分别为∠A ，∠B ，∠C 的对边，下列各式错误的是（ ）A .a =c ·sinAB ．b =c ·cosBC ．b =a ·tanBD ．a =b ·tanA6.在△ABC 中，∠C ＝90°，(1)已知：c ＝ 83，∠A ＝60°，求∠B .a .b ． (2) 已知：a ＝36， ∠A ＝30°，求∠B .b .c .7.（2009·漳州中考）三角形在方格纸中的位置如图所示，则tan 的值是（ ）A ．35B ．43 C ．34D ．45练习:1.在Rt △ABC 中，∠C 为直角，若sinA =53，则cosB =_________． 2.已知cosA =23，且∠B =900-∠A ，则sinB =__________． 3.∠A 为锐角，已知sinA =135，那么cos (900-A)=___________ ． 4.在Rt △ABC 中，∠C 为直角，AC =4，BC =3，则sinA =（ ） A ．43 B ．34 C ． 53 D ．54 5.在Rt △ABC 中，∠C 为直角，sinA =22，则cosB 的值是( ) A ．21 B ．23 C ．1D ．22知识点二、特殊角所对的三角函数值1. 0°.30°.45°.60°.90°特殊角的三角函数值(重要)三角函数0° 30°45°60°90° αsin0 2122 231 αcos1 23 22210 αtan 0 331 3- αcot-3133注意：记忆特殊角的三角函数值，可用下述方法：0°.30°.45°.60°.90°的正弦值分别是02.12.22.32.42，而它们的余弦值分别是42.32.22.12.02；30°.45°.60°的正切值分别是13.22.31，而它们的余切值分别是31.22.13。

三角函数的计算一、锐角三角函数的概念与计算方法1.正弦（sine）函数：正弦函数是指在直角三角形中，锐角的对边与斜边的比值。

其计算公式为：sinθ = 对边 / 斜边。

2.余弦（cosine）函数：余弦函数是指在直角三角形中，锐角的邻边与斜边的比值。

其计算公式为：cosθ = 邻边 / 斜边。

3.正切（tangent）函数：正切函数是指在直角三角形中，锐角的对边与邻边的比值。

其计算公式为：tanθ = 对边 / 邻边。

二、钝角三角函数的概念与计算方法1.余切（cotangent）函数：余切函数是指在直角三角形中，钝角的对边与邻边的比值的倒数。

其计算公式为：cotθ = 邻边 / 对边。

2.余弦（secant）函数：余弦函数是指在直角三角形中，钝角的邻边与斜边的比值的倒数。

其计算公式为：secθ = 斜边 / 邻边。

3.正割（cosecant）函数：正割函数是指在直角三角形中，钝角的对边与斜边的比值的倒数。

其计算公式为：cscθ = 斜边 / 对边。

三、特殊角的三角函数值1.30°角的三角函数值：sin30°= 1/2，cos30° = √3/2，tan30°= 1/√3，cot30° = √3，sec30° = 2/√3，csc30° = 2。

2.45°角的三角函数值：sin45° = cos45° = tan45° = 1，cot45° = 1，sec45° = √2，csc45° = √2。

3.60°角的三角函数值：sin60° = √3/2，cos60° = 1/2，tan60° = √3，cot60° = 1/√3，sec60° = 2，csc60° = 2/√3。

四、三角函数的周期性1.正弦函数的周期性：正弦函数的周期为2π，即sin(θ + 2π) = sinθ。

个性化学科优化学案锐角三角函数知识回顾1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

222c b a =+2、如下图，在Rt △ABC 中，∠C 为直角， 则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。

5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)定 义 表达式 取值范围 关 系正弦斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦斜边的邻边A A ∠=cos cbA =cos 1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A A baA =tan0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A A余切的对边的邻边A A A ∠∠=cot abA =cot0cot >A(∠A 为锐角))90cot(tan A A -︒=)90tan(cot A A -︒=B A cot tan = B A tan cot =)90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =对边邻边b斜边 ACBb a cA 90B 90∠-︒=∠︒=∠+∠得由B AA90B 90∠-︒=∠︒=∠+∠得由B A三角函数 0° 30° 45° 60° 90° αsin0 1 αcos1 0 αtan 0 不存在αcot不存在6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。

锐角三角函数公式正弦：sin α=∠α的对边/∠α的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边面积公式长方形，正方形以及圆的面积公式面积公式包括扇形面积共式，圆形面积公式，弓形面积公式，菱形面积公式，三角形面积公式，梯形面积公式等多种图形的面积公式。

扇形面积公式在半径为R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S＝πR^2，所以圆心角为n°的扇形面积：S＝nπR^2÷360比如：半径为1cm的圆，那么所对圆心角为135°的扇形的周长：C＝2R＋nπR÷180＝2×1＋135×3.14×1÷180＝2＋2.355＝4.355(cm)＝43.55(mm)扇形的面积：S＝nπR^2÷360＝135×3.14×1×1÷360＝1.1775(cm^2)=117.75(mm^2)扇形还有另一个面积公式S=1/2lR其中l为弧长，R为半径三角形面积公式任意三角形的面积公式（海伦公式）：S=√p(p-a)(p-b)(p-c), p=（a+b+c）/2,a.b.c,为三角形三边。

证明：证一勾股定理分析：先从三角形最基本的计算公式S△ABC = aha入手，运用勾股定理推导出海伦公式。

证明：如图ha⊥BC，根据勾股定理，得: x = y = ha = = = ∴S△ABC = aha= a× = 此时S△ABC为变形④，故得证。

证二：斯氏定理分析：在证一的基础上运用斯氏定理直接求出ha。

斯氏定理:△ABC边BC上任取一点D，若BD=u，DC=v,AD=t.则t 2 = 证明：由证一可知，u = v = ∴ha 2 = t 2 = －∴S△ABC = aha = a × = 此时为S△ABC的变形⑤，故得证。

初三锐角三角函数题型及解题方法初三数学中，锐角三角函数是一个非常重要的内容。

学习锐角三角函数，不仅需要掌握其概念和公式，还需要掌握一些常见的题型及解题方法。

本文将介绍一些常见的锐角三角函数题型及解题方法，帮助初三学生更好地掌握这一内容。

一、求三角函数值求三角函数值是锐角三角函数中最基本的题型。

一般来说，题目都会给出三角函数的角度，要求求出其对应的正弦、余弦、正切等函数值。

解题方法：对于这类题目，我们需要掌握三角函数的定义和公式。

例如，正弦函数的定义是：在直角三角形中，对于一个锐角角度A，其对边长度与斜边长度的比值称为正弦值sinA。

因此，我们只需要根据这个定义和公式进行计算即可。

举个例子，题目给出角度A=30度，要求求出其正弦值sinA。

根据正弦函数的定义和公式，我们得到：sinA=对边长度/斜边长度=sqrt(3)/2因此，sinA=√3/2。

二、三角函数的基本关系式三角函数的基本关系式指的是三角函数之间的基本等式。

例如，正切函数的基本关系式是tanA=sinA/cosA。

这类题目一般要求将一个三角函数用另外一个三角函数表示出来，或者将两个三角函数相互表示。

解题方法：对于这类题目，我们需要掌握三角函数之间的基本关系式。

例如，正切函数的基本关系式是：tanA=sinA/cosA因此，如果题目给出sinA的值，要求求出tanA的值，我们只需要将sinA/cosA代入上式，即可得到：tanA=sinA/cosA=√3/3三、三角函数值的范围三角函数值的范围是指，每个三角函数的取值范围。

例如，正弦函数的取值范围是[-1,1]，余弦函数的取值范围也是[-1,1]。

解题方法：对于这类题目，我们需要掌握每个三角函数的取值范围。

例如，正弦函数的取值范围是[-1,1]，因此，如果题目给出sinA=-0.5，我们就可以知道sinA的值在[-1,1]范围之内。

四、三角函数的性质三角函数的性质指的是，它们在不同象限中的正负性和大小关系。

用锐角三角函数概念解题的常见方法(含答案11页)用锐角三角函数概念解题的常见方法1．锐角三角函数（1）锐角三角函数的定义我们规定：sinA=abab，cosA=，tanA=，cotA=．ccba锐角的正弦、余弦、正切、余切统称为锐角的三角函数．（2）用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算，甚至可以背诵下来，但是对于一般的锐角又怎样求它的三角函数值呢？用计算器可以帮我们解决大问题．①已知角求三角函数值；②已知三角函数值求锐角．2直角三角形中，30°的锐角所对的直角边等于斜边的一半．3．锐角三角函数的性质（1）0&lt;sinα&lt;1，o&lt;cosα&lt;1（0°&lt;α&lt;90°）1（2）tanα·cotα=1或tanα=（3）tanα=1；cot?sin?cos?，cotα=．cos?sin?（4）sinα=cos（90°-α），tanα=cot（90°-α）．有关锐角三角函数的问题，常用下面几种方法：一、设参数例1. 在?ABC中，?C?90?，如果tanA?5，那么sinB的值等于（）12D.12 5A.513B.1213C.512解析：如图1，要求sinB的值，就是求AC5的值，而已知的tanA?，也就是AB12BC5? AC12可设BC?5k，AC?12k则AB?(5k)2?(12k)2?13k?sinB?12k12?，选B 13k13二、巧代换例2. 已知tan??3，求sin??2cos?的值。

5sin??cos?解析：已知是正切值，而所求的是有关正弦、余弦的值，我们可以利用关系式sin??3，作代换sin??3cos?，代入即可达到约分的目的，也可以把所求的cos?分式的分子、分母都除以cos?。

tan??2sin??2sin??2cos? ?cos?sin5sin??cos?5?1cos?再把sin?1?3代入，得：原式? cos?16三、妙估计例3. 若太阳光与地面成37?角，一棵树的影长为10m，则树高h的范围是（取?1.7）A. 3?h?5B. 5?h?10C. 10?h?15D. h?15 解析：如图2，树高h?10tan37?，要确定h的范围，可根据正切函数是增函数，估计tan30??tan37??tan45?即10tan30??10tan37??10tan45??10??h?10 3?5?h?10，故选B四、善转化例4. 在?ABC中，1?A?30?，tanB?BC?，求AB的长。