水锤计算
- 格式:doc
- 大小:992.50 KB
- 文档页数:41

第四节水锤计算的特征线法前面介绍了水锤计算的解析法。
解析法的优点是应用简便,但难以求解较为复杂锤问题。
水锤计算的特征线法原则上可以解决任何形式的边界条件问题,可以较合理应水轮机的特性,能较方便地计人摩阻的影响,也便于用数字计算机计算。
特征线法有两种,一种以ζ-v(或H-V)为坐标场,一种以x-t为坐标场,两法的结果是一致的。
图14-12 简单管示意图一、以ζ-v为坐标场的特征线法图14-12表示一特性沿管长不变的水管,P为管中任意一点,距A点和B点的距离分为和。
根据基本方程式(14-5)和式(14-6)可导出求解P、B、A三点水锤压强时征线方程。
(一)任意断面P的水锤求解根据基本方程式(14-5)和式(15一6),P点在时刻t的压强和流速变化为式中上标“P”表示地点,下标“t”表示时间,例如,表示P点在时刻t的水头,余类推。
对于某一确定的断面P,为一常数,为便于书写,在波函数F和f中略去了。
对于A点,在时刻可写出下列相似的方程因F是由A向P传播的反向波,故。
由于水管特性不变,。
考虑以上关系,将式(a)和式(b)两组方程相减,得以上二式消去f,并将ζ=△H/Ho、v=V/Vmax和ρ=cVmax/2gHo。
对于B点,在时刻可以写出与式(b)相似的方程因f是由B向P传播的正向波,故,将式(c)与(a)两组方程相减,以上法处理,得从形式上看,式(14-35)是反x向写出的,称之为反向方程,在ζ-v坐标场上是一根斜率为2ρ的直线,如图14-13中的线;式(9-36)是顺x向写出的方程,成为正向方程,在ζ-v坐标场上是一根斜率为-2ρ的直线,如图14-13中的线。
图14-13 ζ-v坐标场上得特征线在式(14-35)和式(14-36)中,如已知A点在时刻和B点在时刻的压强和流速,即可求出P点在时刻t的压强和流速。
和为图14-13中Pt的坐标值,可用和两条直线的交点求出。
用特征线法求解压强和流速的方法就是过去广为采用的水锤计算的图解法。

水锤计算解析法例题
【最新版】
目录
1.解析水锤计算的概念和原理
2.介绍水锤计算的解析法例题
3.分析例题的解题过程和方法
4.总结水锤计算解析法的应用和意义
正文
水锤计算是流体力学中的一个重要概念,它是指在管道中由于流速的突然变化而引起的压力变化。
这种压力变化会对管道产生冲击,从而影响管道的安全运行。
因此,对水锤计算的研究具有重要的实际意义。
解析法是水锤计算中的一种常用方法,它通过解析公式来计算水锤压力,从而为工程应用提供理论依据。
下面,我们将通过一个例题来介绍水锤计算解析法的具体应用。
例题:在一条长为 100m 的管道中,流速突然从 5m/s 减小到 1m/s,求水锤压力。
解题过程如下:
1.根据水锤计算的原理,首先需要求出流速的变化量Δu,即Δ
u=u2-u1=1m/s-5m/s=-4m/s。
2.计算水锤压力的解析公式为:Δp=ρ*Δu*L/2,其中ρ为流体密度,L 为管道长度。
题目中未给出流体密度,我们可以假设为水的密度ρ
=1000kg/m。
3.将已知数据代入公式,得到Δ
p=1000kg/m*(-4m/s)*100m/2=-200000Pa。
因此,水锤压力为 -200000Pa。
注意,这里的负号表示水锤压力是负
的,即管道受到了压缩。
通过以上例题,我们可以看到,水锤计算解析法是一种有效的计算方法,它可以帮助我们快速准确地计算水锤压力,从而为工程应用提供理论支持。


水锤压力计算(一)
(1)根据小水电运行情况,水锤压力计算按以下两种工况计算:
a. 水库正常蓄水位 2180.0m 时,机组突然丢弃全部负荷。
b.小水电运行限制水位 2178.0m 时,机组由空转至满负荷运行。
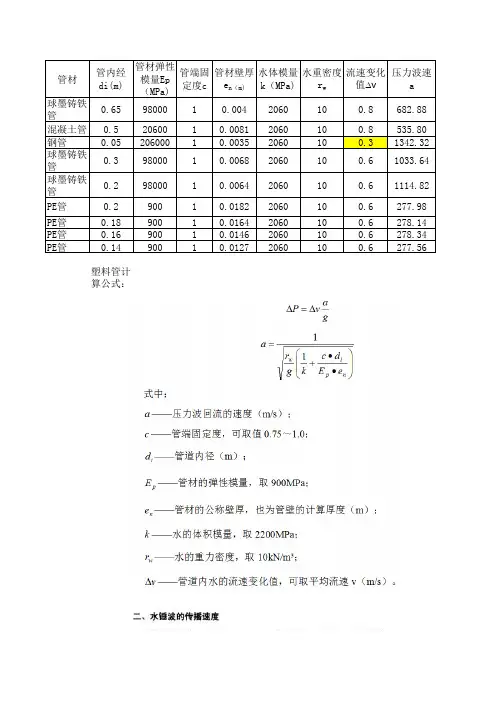
(2)水锤计算基本公式:
a. 钢管中水锤波传播速度α值:
式中 1425—声波在水中的传播速度(m/s );
ε—水的弹性模量,ε=2.1×104(kg/cm 2);
E —管壁的弹性模量,E 钢=2.1×106(kg/cm 2);
D —压力管道的内径(mm );
δ—管壁厚度(mm )。
b. 水锤波在水管中传播来回一次所需时间:
式中 L —压力钢管总长度(m );
α—水锤波传播速度(m/s )。
c. 压力水管特性常数:
式中 ρ、σ—钢管特性常数;
H —水电站的静水头(m );
V —钢管中水流流速 (m/s );
Ts —导叶关闭时间 Ts=5s 。
(3) 经过计算判断得压力钢管内水锤为间接水锤,最大值为极限水锤,水锤压力沿程分布计算成果见表1.3.1。
压力钢管水锤压力计算成果表
gH V 2αρ=
gHTs
LV
=σδ
εαD
E +=11425
α
L
t r 2=
(4)水锤压力沿程分布曲线见附图1.1.1。

第一节概述一、水电站的不稳定工况机组在稳定运行时,水轮机的出力与负荷相互平衡,这时机组转速不变,水电站有压引水系统(压力隧洞、压力管道、蜗壳及尾水管)中水流处于恒定流状态。
在实际运行过程中,电力系统的负荷有时会发生突然变化(如因事故突然丢弃负荷,或在较短的时间内启动机组或增加负荷),破坏了水轮机与发电机负荷之间的平衡,机组转速就会发生变化。
此时水电站的自动调速器迅速调节导叶开度,改变水轮机的引用流量,使水轮机的出力与发电机负荷达到新的平衡,机组转速恢复到原来的额定转速。
由于负荷的变化而引起导水叶开度、水轮机流量、水电站水头、机组转速的变化,称为水电站的不稳定工况。
其主要表现为:(1) 引起机组转速的较大变化由于发电机负荷的变化是瞬时发生的,而导叶的启闭需要一定时间,水轮机出力不能及时地发生相应变化,因而破坏了水轮机出力和发电机负荷之间的平衡,导致了机组转速的变化。
丢弃负荷时,水轮机在导叶关闭过程中产生的剩余能量将转化为机组转动部分的动能,从而使机组转速升高。
反之增加负荷时机组转速降低.(2) 在有压引水管道中发生“水锤"现象当水轮机流量发生变化时,管道中的流量和流速也要发生急剧变化,由于水流惯性的影响,流速的突然变化使压力水管、蜗壳及尾水管中的压力随之变化,即产生水锤。
导叶关闭时,在压力管道和蜗壳中将引起压力上升,尾水管中则造成压力下降。
反之导叶开启时,在压力管道和蜗壳内引起压力下降,而在尾水管中引起压力上升。
(3) 在无压引水系统(渠道、压力前池)中产生水位波动现象。
无压引水系统中产生的水位波动计算在第八章已介绍。
二、调节保证计算的任务水锤压力和机组转速变化的计算,一般称为调节保证计算.调节保证计算的任务及目的是:(1)计算有压引水系统的最大和最小内水压力。
最大内水压力作为设计或校核压力管道、蜗壳和水轮机强度的依据之一;最小内水压力作为压力管道线路布置、防止压力管道中产生负压和校核尾水管内真空度的依据。

第三节水锤计算的解析法-CAL-FENGHAI.-(YICAI)-Company One1第三节水锤计算的解析法一、直接水锤和间接水锤(一)直接水锤若水轮机开度的调节时间≤ 2L/c,则在水库反射波到达水管末端之前开度变化已经结束,水管末端只受因开度变化直接引起的水锤波的影响,这种现象习惯上称为直接水锤。
由于水管末端未受水库反射波的影响,故基本方程式(14-5)和式(14-6)中的函数f(t-x/c),用以上二式消去F(t+x/c)的直接水锤公式从式(14-13)可以看出,当开度关闭时,管内流速减小,括号内为负值,△H为正,发生正水锤,反之,当开启时,△H为负,发生负水锤。
直接水锤的压强界与流速变(V -Vo )和水管特性(反映在波速c 中)有关,而与开度的变化速度、变化规律和水管长度无关。
若管道中的初始流速Vo=5m/s,波速c=1000m/s,在丢弃全负荷时若发生直接水锤,△H将达510m,因此在水电站中直接水锤是应当绝对避免的。
(二)间接水锤若水轮机开度的调节时间>2L/c,则在开度变化终了之前水管进口的反射波已经到达水管末端,此反射波在水管末端将发生再反射,因此水管末端的水锤压强是由向上游传播的水锤波F和反回水管本端的水锤波f叠加的结果,这种水锤现象习惯上称为间接水锤。
显然,间接水锤的计算要比直接水锤复杂得多。
间接水锤是水电站中经常发生的水锤现象,也是我们要研究的主要对象。
二、水锤的连锁方程利用基本方程求解水锤问题,必须利用已知的初始条件和边界条件。
初始条件是水轮机开度未发生变化时的情况,此时管道中为恒定流,压强和流速都是已知的。
对于图14-1的简单管,边界条件是利用A、B两点。
B点的压强为常数,令ζ=△H/Ho,则=0,水锤波在B点发生异号等值反射。
A点的边界条件较为复杂,决定于节流机构的出流规律。
从《水力学》中我们知道水斗式水轮机喷嘴的边界条件可表达为式中v-管道中的相对流速,V=V/Vmax., V为管道中任意时刻的流速,Vmax为最大流速;τ-喷嘴的相对开度,, w为喷嘴任意时刻的过水面积,为最大面积;ζ-水锤相对压强,ζ=(H-Ho)/Ho,H为管末任意时刻的压力水头,Ho为初始水头。

长距离输水水锤计算的方法与计算公式水锤压力的作用原理──管路内的水系统,系统内任一点水压力的瞬间变化,造成整个水管路系统的压力巨变。
改善与防止(1).改善─系统的压力变化幅度降低,压力变化时间延长水锤压力是以sin,或cos函数曲线变化,说明如下:1. F 大,则T 小2. F 小,则T 大→ 上图中蓝色曲线是改善的方法。
降低瞬间压力升降的F值,延长水锤压力作用的时间管路必须做应力分析,从应力分析曲线选择安装水锤压力吸收器。
如果随便找个地方安装,毫无学问与专业,就不必念书了。
(2)防止─ 从管路设计开始,管路系统平衡的设计,管路材料的选择,‧‧‧等管路材料的选择是唯一最正确的防止方法。
Vw = 1/n ×√K/PTc =2L / Vw△Hfr =Vw ×△Vr /g其中,n= √ 1+ ID × K / E × SP或n= 1+ √ ID×K×(1.25-μ)/ E×SP上项方程式中ID 管的内径SP 管的厚度E 管材料的弹性系数μ Poisson 常数K 流体的buckling valueP 流体密度Tc 水锤发生的时间L 管路长度瞬间最大压力由以上的数学方程式,管子的材料选择100%掌控值的大小。
这个=F,愈小愈好;愈大愈不好。
上图中的F就是。
如果有需要可与我联系。
该系统不但可以降低噪音到50db以下,也可以防止水锤造成的噪音与管路的伤害。
缴税款。
纳税人未按照规定期限缴纳税款的,扣缴义务人未按照规定期限解缴税款的,税务机关除责令限期缴纳外,从滞纳税款之日起,按日加收滞纳税款0.5‰的滞纳金。

复杂管道水锤计算在实际工程中,常见的是复杂管路系统,共有三种类型 (1)串联管:管壁厚度、直径和材料随水头增加自上而下逐 段改变。
(2)分岔管: 这在分组供水和联合供水中经常遇到。
(3)蜗壳和尾水管: 装有反击式水轮机的管道系统,应考 虑蜗壳和尾水管的影响,而且其过流特性与孔口出流不 一样,流量不仅与作用水头有关,而且与水轮机的机型 和转速有关。
一、串联管水锤的简化计算等价水管法: 把串联管转化为等价的简单管来计算 等价原则: 管长、相长、管中水体动能与原管相同设一根串联管的管道特性为:L1,V1,c1; L2,V2,c2; …… ;Ln,Vn,cn(1) (2) 等价管的总长为:L=∑Li =1ni根据管中水体动能不变的要求:LVm=L1V1+L2V2+……+LnVn=∑LiVi , + + ∑由此可得加权平均流速:Vm =(3)∑ LVi =1ni iL根据相长不变的要求,水锤波按平均波速由断面A传到断面B所需的时间等于水锤波在各段传播时间的总和, 即L L1 L2 Ln Li = + + LL + =∑ cm c1 c2 cn i =1 cincm =L∑ni =1Li ci对于间接水锤,管道的平均特性常数为a mVm ρm = 2gH 0 gLVm σ m= gH 0Ts2L tr = am求出管道平均特性常数后,可按简单管的间接水锤计 算公式求出复杂管道的间接水锤值。
二、分岔管的水锤压力计算分岔管的水锤计算方法之一是截肢法。
特点:当机组同时关闭时,选取总长为最大的一根支管, 将其余的支管截掉,变成串联管道,然后用各管段中实际流 量求出各管段的流速,再用加权平均的方法求出串联管中的 平均流速和平均波速,最后采用串联管的简化公式相应地求 出水击值。
三、蜗壳、尾水管水锤压力计算(1) 首先将蜗壳视作压力水管的延续部分,并假想把导叶移 至蜗壳的末端,尾水管也作为压力管道的一部分,把压力管 道、蜗壳和尾水管组合视为一串联管,再将该串联管简化 为等价简单管进行计算。


第三节水锤计算的解析法一、直接水锤和间接水锤(一)直接水锤若水轮机开度的调节时间≤ 2L/c,则在水库反射波到达水管末端之前开度变化已经结束,水管末端只受因开度变化直接引起的水锤波的影响,这种现象习惯上称为直接水锤。
由于水管末端未受水库反射波的影响,故基本方程式(14-5)和式(14-6)中的函数f(t-x/c),用以上二式消去F(t+x/c)的直接水锤公式从式(14-13)可以看出,当开度关闭时,管内流速减小,括号内为负值,△H为正,发生正水锤,反之,当开启时,△H为负,发生负水锤。
直接水锤的压强界与流速变(V -Vo )和水管特性(反映在波速c中)有关,而与开度的变化速度、变化规律和水管长度无关。
若管道中的初始流速Vo=5m/s,波速c=1000m/s,在丢弃全负荷时若发生直接水锤,△H将达510m,因此在水电站中直接水锤是应当绝对避免的。
(二)间接水锤若水轮机开度的调节时间>2L/c,则在开度变化终了之前水管进口的反射波已经到达水管末端,此反射波在水管末端将发生再反射,因此水管末端的水锤压强是由向上游传播的水锤波F和反回水管本端的水锤波f叠加的结果,这种水锤现象习惯上称为间接水锤。
显然,间接水锤的计算要比直接水锤复杂得多。
间接水锤是水电站中经常发生的水锤现象,也是我们要研究的主要对象。
二、水锤的连锁方程利用基本方程求解水锤问题,必须利用已知的初始条件和边界条件。
初始条件是水轮机开度未发生变化时的情况,此时管道中为恒定流,压强和流速都是已知的。
对于图14-1的简单管,边界条件是利用A、B两点。
B点的压强为常数,令ζ=△H/Ho,则=0,水锤波在B点发生异号等值反射。
A点的边界条件较为复杂,决定于节流机构的出流规律。
从《水力学》中我们知道水斗式水轮机喷嘴的边界条件可表达为式中v-管道中的相对流速,V=V/Vmax., V为管道中任意时刻的流速,Vmax为最大流速;τ-喷嘴的相对开度,, w为喷嘴任意时刻的过水面积,为最大面积;ζ-水锤相对压强,ζ=(H-Ho)/Ho,H为管末任意时刻的压力水头,Ho为初始水头。
第五节复杂管路的水锤计算直到目前为止,我们讨论的都是简单管中的水锤问题。
简单管是指直径、管壁厚度和材料均不随管长变化的水管。
在实际工程中,简单管是不多见的,经常遇到的是复杂管。
复杂管有两种:一种是管径和管壁厚度自上而下随着水头的增加而逐段改变的水管,这种水管有时称为串联管;另一种是分岔管,这在集中供水中经常遇到。
无论是串联管或分岔管,水锤波在水管特性变化处都将发生反射,从而使水锤现象更为复杂。
一、串联管的水锤串联管各段的流速V和波速c不同,因此特性系数ρ和σ各异。
用特征线法可精确求出管道各点的水锤变化过程,管道特性变化点应选为计算网格的结点,各管段的特征方程则用相应管段的有关参数列出。
对于图14-12所示的压力管道,若AP和PB两段的特性不同,其流速(或断面积)和波速分别为(或)、和(或)、,则这两段管道的特征方程的系数和特征线的斜率均应采用其相应的流速(或断面积)和波速求出,经过这样的调整以后,即可按前述的方法和步骤进行串联管的水锤计算。
若水锤波通过AP段水管的历时为,通过PB段水管的历时为,则最大的计算时间步长为两者最大公约数的2倍,若最大公约数很小,则计算时间步长小,计算工作量大。
若串联管由许多段组成,则计算更为繁琐。
因此,在实践中常把串联管转化为等价的简单计算,研究证明,由此简化带来的误差不大。
这种简化的计算方法称“等价水管法”,现介绍如下。
图14-16 串联管示意图设串联管如图14-16所示,各段的长度、流速和水锤波速分别示于图中。
现用一等价的简单管代替,其流速和水锤波速分别以Ve和表示,此等价管应满足以下要求:长度与原管相同;相长与原管相同;管中水体动能与原管相同。
后两项要求是必要的。
根据相长不变的要求得根据水体动能不变的要求得等价管的特性常数利用和,即可将串联管作为简单管用前面介绍的任何方法进行计算。
二、分岔管的水锤计算图14-17表示一分岔管。
分岔管水锤计算的关键是求解分岔点P的压强和流速。
水锤效应计算公式水锤效应计算公式。
水锤效应是指在管道系统中由于液体流动突然停止或改变方向而产生的压力波动现象。
这种现象可能会对管道系统造成严重的损坏,因此对水锤效应进行计算和控制至关重要。
本文将介绍水锤效应的计算公式,并讨论如何有效地控制水锤效应。
水锤效应的计算公式可以通过水锤方程来表示。
水锤方程描述了液体在管道中运动时的压力变化情况。
水锤方程的一般形式如下:ΔP = ρ V ΔV。
其中,ΔP表示压力变化,ρ表示液体的密度,V表示流速,ΔV表示流速的变化。
根据水锤方程,当液体的流速突然改变时,会产生压力波动,从而导致水锤效应的发生。
为了更好地理解水锤效应的计算公式,我们可以通过一个实际的例子来说明。
假设有一条长为100米的水平管道,管道内的水流速为10m/s。
如果突然关闭了管道的阀门,导致水流速瞬间降为0,那么根据水锤方程,可以计算出压力的变化。
假设水的密度为1000kg/m³,那么根据水锤方程,压力变化ΔP可以计算如下:ΔP = 1000 10 10 = 100000Pa。
这意味着在管道中会产生10万帕的压力波动,这种压力波动可能会对管道系统造成严重的损坏。
为了有效地控制水锤效应,我们可以采取一些措施。
首先,可以通过合理设计管道系统来减小水锤效应的发生。
例如,可以在管道系统中设置缓冲器或减压阀来减缓压力波动的影响。
其次,可以通过控制阀门的开启和关闭速度来减小水锤效应的发生。
此外,还可以通过改变管道的设计参数,如管道的直径和材质等,来减小水锤效应的影响。
除了以上措施外,还可以通过数值模拟和实验研究来进一步探讨水锤效应的计算和控制。
通过数值模拟,可以对管道系统中水锤效应的发生进行模拟和预测,从而找到合适的控制方法。
通过实验研究,可以验证水锤效应的计算公式,并找到更加有效的控制方法。
总之,水锤效应的计算公式可以通过水锤方程来表示,通过对水锤方程的计算,可以预测和控制管道系统中水锤效应的发生。
第三节水锤计算的解析法(总13页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第三节水锤计算的解析法一、直接水锤和间接水锤(一)直接水锤若水轮机开度的调节时间≤ 2L/c,则在水库反射波到达水管末端之前开度变化已经结束,水管末端只受因开度变化直接引起的水锤波的影响,这种现象习惯上称为直接水锤。
由于水管末端未受水库反射波的影响,故基本方程式(14-5)和式(14-6)中的函数f(t-x/c),用以上二式消去F(t+x/c)的直接水锤公式从式(14-13)可以看出,当开度关闭时,管内流速减小,括号内为负值,△H为正,发生正水锤,反之,当开启时,△H为负,发生负水锤。
直接水锤的压强界与流速变(V -Vo )和水管特性(反映在波速c 中)有关,而与开度的变化速度、变化规律和水管长度无关。
若管道中的初始流速Vo=5m/s,波速c=1000m/s,在丢弃全负荷时若发生直接水锤,△H将达510m,因此在水电站中直接水锤是应当绝对避免的。
(二)间接水锤若水轮机开度的调节时间>2L/c,则在开度变化终了之前水管进口的反射波已经到达水管末端,此反射波在水管末端将发生再反射,因此水管末端的水锤压强是由向上游传播的水锤波F和反回水管本端的水锤波f叠加的结果,这种水锤现象习惯上称为间接水锤。
显然,间接水锤的计算要比直接水锤复杂得多。
间接水锤是水电站中经常发生的水锤现象,也是我们要研究的主要对象。
二、水锤的连锁方程利用基本方程求解水锤问题,必须利用已知的初始条件和边界条件。
初始条件是水轮机开度未发生变化时的情况,此时管道中为恒定流,压强和流速都是已知的。
对于图14-1的简单管,边界条件是利用A、B两点。
B点的压强为常数,令ζ=△H/Ho,则=0,水锤波在B点发生异号等值反射。
A点的边界条件较为复杂,决定于节流机构的出流规律。
从《水力学》中我们知道水斗式水轮机喷嘴的边界条件可表达为式中v-管道中的相对流速,V=V/Vmax., V为管道中任意时刻的流速,Vmax为最大流速;τ-喷嘴的相对开度,, w为喷嘴任意时刻的过水面积,为最大面积;ζ-水锤相对压强,ζ=(H-Ho)/Ho,H为管末任意时刻的压力水头,Ho为初始水头。
第九章水电站的水锤与调节保证计算第一节概述一、水电站的不稳定工况机组在稳定运行时,水轮机的出力与负荷相互平衡,这时机组转速不变,水电站有压引水系统(压力隧洞、压力管道、蜗壳及尾水管)中水流处于恒定流状态。
在实际运行过程中,电力系统的负荷有时会发生突然变化(如因事故突然丢弃负荷,或在较短的时间内启动机组或增加负荷),破坏了水轮机与发电机负荷之间的平衡,机组转速就会发生变化。
此时水电站的自动调速器迅速调节导叶开度,改变水轮机的引用流量,使水轮机的出力与发电机负荷达到新的平衡,机组转速恢复到原来的额定转速。
由于负荷的变化而引起导水叶开度、水轮机流量、水电站水头、机组转速的变化,称为水电站的不稳定工况。
其主要表现为:(1) 引起机组转速的较大变化由于发电机负荷的变化是瞬时发生的,而导叶的启闭需要一定时间,水轮机出力不能及时地发生相应变化,因而破坏了水轮机出力和发电机负荷之间的平衡,导致了机组转速的变化。
丢弃负荷时,水轮机在导叶关闭过程中产生的剩余能量将转化为机组转动部分的动能,从而使机组转速升高。
反之增加负荷时机组转速降低。
(2) 在有压引水管道中发生“水锤”现象当水轮机流量发生变化时,管道中的流量和流速也要发生急剧变化,由于水流惯性的影响,流速的突然变化使压力水管、蜗壳及尾水管中的压力随之变化,即产生水锤。
导叶关闭时,在压力管道和蜗壳中将引起压力上升,尾水管中则造成压力下降。
反之导叶开启时,在压力管道和蜗壳内引起压力下降,而在尾水管中引起压力上升。
(3) 在无压引水系统(渠道、压力前池)中产生水位波动现象。
无压引水系统中产生的水位波动计算在第八章已介绍。
二、调节保证计算的任务水锤压力和机组转速变化的计算,一般称为调节保证计算。
调节保证计算的任务及目的是:(1) 计算有压引水系统的最大和最小内水压力。
最大内水压力作为设计或校核压力管道、蜗壳和水轮机强度的依据之一;最小内水压力作为压力管道线路布置、防止压力管道中产生负压和校核尾水管内真空度的依据。
(2) 计算丢弃负荷和增加负荷时的机组转速变化率,并检验其是否在允许范围内。
(3) 选择水轮机调速器合理的调节时间和调节规律,保证压力和转速变化不超过规定的允许值。
(4) 研究减小水锤压力及机组转速变化率的措施。
第二节水锤现象及其传播速度一、水锤现象在水电站运行过程中,为了适应负荷变化或由于事故原因,而突然启闭水轮机导叶时,由于水流具有较大惯性,进入水轮机的流量迅速改变,流速的突然变化使压力水管、蜗壳及尾水管中的压力随之变化,这种变化是交替升降的一种波动,这种现象称为水锤。
要正确解释和理解水锤现象及其实质,在研究水锤过程中必须考虑水的压缩性及管壁弹性的影响。
为了便于说明问题,假定水管材料、管壁厚度、直径沿管长不变,不计管道摩阻损失,阀门突然关闭,见图9-1。
水锤现象有下面几个典型的过程。
(1)t=0~L/a。
当阀门突然关闭(即关闭时间T s=0)后,在dt1时段内,紧靠阀门处管段dx1 中的水体首先发生变化,流速由V0变为零,压力上升为H0+△H;与此同时,水体被压缩,水的密度变成为ρ+△ρ管壁膨胀,从而腾出了空间,得以容纳dx1以上管段仍以V0速度流动来的水体。
也就是说,在dt1时段内,dx1管段以上仍未受到水锤的影图9-1 压力水管水击过程响。
之后依次再经dt2 、dt3、…时段,在dx2、dx3、…管段中流速、压力将相继发生同样的变化,见图9-1(a)。
这样,一段接一段地将阀门关闭的影响向上游传播,压力增加如同波一样自阀门A处沿管道逐渐向上游传播,这就是水锤波,其传播速度称之为水锤波速a,变化的压力△H称为水锤压力。
使压力增加的波为增压波,使压力降低的波叫降压波。
经过L/a 时间,水锤波达到管道进口处,此时,整个水管内的流速V0降为零,压力上升为H0+△H。
(2) t=L/a~2L/a。
当t=L/a时,水锤波将传至水库点D处,由于D点右端管道内压力为H0+△H,而左端水库保持不变为H,因此“边界”处的水体不能保持平衡,管道中的水体在△H压差作用下将逆流向水库。
在t=L/a后的dt1时段内,首先是紧靠水库dx n管段内发生变化,流速将由0变为-V0,压力由H0+△H变为H0;管壁及水体随着水锤压力的消失恢复至原状。
同理接再经dt2 、dt3 、…时段,在相应dx n-1、dx n-2、dx n-3…管段中将发生同样的变化,如图9-1(b)。
直到t=2L/a时刻,整个管道中的压力、流速、管径及水的密度均恢复到初始状态。
这说明,水锤波在水库处要发生反射,反,但符号相反,射特点是“等值异号”反射,即反向波与入射波的数值相同,均为H升压波反射为降压波。
(3) t=2L/a~3L/a。
当t=2L/a时,水锤波传播到阀门处A点,由于阀门已关闭,加之水流的惯性作用,管道中的水继续流向水库。
在t=2L/a~3L/a时段内,首先是紧近阀门dx1管段内发生变化,依次传到dx2、dx3…管段,到3L/a时刻,流速将由-V0变为0,压力由H0变为H0-△H,管径为D-△D,水的密度变为ρ-△ρ。
当阀门全关闭时,水锤波在阀门处的反射特点是“等值同号”反射,即反向波与入射波的数值和符号不变,从水库传来降压波仍反射为降压波。
(4)t=3L/a~4L/a。
当t=3L/a时,水锤波又回到水库处D点,由于管道压力比水库低△H,则D点压力不能维持平衡,因此水库的水又向阀方向流动,这时水库将阀门反射回来的降压波又反射为升压波,到t=4L/a时,管道流速将由0变为V0,压力由H0-△H0变为H0,管径、水密度都恢复到初始状态。
T=4L/a称为水锤波的“周期”。
每经一个周期,水锤现象就重复一次上述过程。
水锤波在管中传播一个来回的时间t r=2L/a,称之为“相”,两个相为一个周期T=2t r。
阀门突然开启时,水锤现象与上述情况相反。
如果不存在水力摩阻,则上述的水锤过程将无休止地反复下去,但由于水力摩阻的存在,水锤过程不可能无休止地振荡下去,压力波因摩擦损失而逐渐衰减,在一定时段内逐渐消失。
综上所述,我们可以初步得出以下几点结论:(1) 水锤压力实际上是由于水流速度变化而产生的惯性力。
当突然启闭阀门时,由于启闭时间短、流量变化快,因而水锤压力往往较大,而且整个变化过程是较快的。
(2) 由于管壁具有弹性和水体的压缩性,水锤压力将以弹性波的形式沿管道传播。
(3) 水锤波同其它弹性波一样,在波的传播过程中,外部条件发生变化处(即边界处)均要发生波的反射。
其反射特性(指反射波的数值及方向)决定于边界处的物理特性。
二、水锤波的传播速度在水锤过程的分析与计算中,波速是一个重要的参数。
它的大小与管壁材料、厚度、管径、管道的支承方式以及水的弹性模量等有关。
由水流的连续方程并考虑水体和管壁的弹性后,可导出水锤波的传播速度为)/(114351/s m EDK E DKKg a δδγ+=+= (9-1) 式中 K ——水的体积弹性模量,一般为2.06×103MPa ;E ——管壁材料的纵向弹性模量(钢村E =2.06×105MPa ,铸铁E =0.98×105MPa ,混凝土E =2.06×104MPa);g ——重力加速度;D ——管道内径;δ——管壁厚度。
γ/Kg 为声波在水中的传播速度,随水温度和压力的升高而加大,一般可取为1 435m/s 。
在缺乏资料的情况下,露天钢管的水锤波速可近似地取为1 000m/s ,埋藏式钢管可近似取为1 200m/s ,钢筋混凝土管可取900m/s~1 200m/s 。
第三节 水锤基本方程及边界条件为求解水锤压力升高问题,需要建立基本方程。
基本方程与相应的边界条件联立,用解析方法或数值计算方法求解水锤值及其变化过程。
一、水锤基本方程(一)、基本方程对有压管道而言,不论在何种情况下都应满足水流的运动方程及连续方程。
当水管材料、厚度及直径沿管长不变时,其运动方程为:02=+∂∂+∂∂+∂∂V V Df x V V t V x Hg (9-2)将管道材料及水体当作弹性体考虑,其连续方程为:02=∂∂+∂∂+∂∂xH V x V g a t H (9-3) 式中 H ——压力水头;V ——管道中的流速,向下游为正;a ——水锤波传播速度;f —— 水流摩擦阻力系数;D ——管道直径;x ——距离,其正方向与流速取为一致;t ——时间。
上面二式中,因流速V 与波速a 相比数量较小,故可忽略x V V ∂∂和xH V ∂∂项。
另外,为了简化计算,使方程线性化,忽略摩擦阻力的影响。
当x 轴改为取阀门端为原点,向上游为正时,如图9-2,方程(9-2)、(9-3)可简化为:tV x H g ∂∂=∂∂ (9-4) xV g a t H ∂∂=∂∂2 (9-5) 式(9-4)和式(9-5)为一组双曲线型偏微分方程,其通解为: )()(0a x t f a x t F H H H ++-=-=∆ (9-6) ⎥⎦⎤⎢⎣⎡+---=-=∆)()(0a x t f a x t F a gV V V (9-7) 式中H 0和V 0为初始水头和流速;F 和f 分别为两个波函数,其量纲与水头H 相同,故可视为压力波。
F (t -x /a )表示以波速a 沿x 轴负方向传播的压力波,即逆水流方向移动的压力波,称为逆流波;f (t +x /a )表示以波速a沿x 轴正方向传播的压力波,即顺水流方向移动的压力波,称为顺流波。
任何断面任何时刻的水锤压力值等于两个方向相反的压力波之和,而流速值为两个压力波之差再乘以-g/a 。
如果知道了t 时刻在x 位置处的水锤波函数F (t -x /a ),则当时间变为t 1=t +Δt ,研究x 1=x+a Δt 处的逆流波函数 图9-2 水击计算示意图⎪⎭⎫ ⎝⎛∆+-∆+=-a t a x t t F a x t F )/(11=)/(a x t F -, 其值不变,证明了F (t -x /a )沿逆水流方向的传播特性。
反之研究t 1=t +Δt 时刻在位置x 1=x-a Δt 处的顺流波函数,可以证明f (t +x /a ) 沿顺水流方向的传播特性。
(二)、水锤计算的连锁方程若已知断面A(见图9-2)在时刻t 的压力为A t H ,流速为At V ,由(9-6)和(9-7)消去f 后,得: )(2)(00ax t F V V g a H H A t A t -=--- 同理可写出a L t /=∆时刻后B 点的压力和流速的关系:)(2)(00aL x t t F V V g a H H B t t B t t +-∆+=---∆+∆+ 由于)/(]/)()[(a x t F a L x t t F -=+-∆+,由上述二式得()A t B t t A t B t t V V ga H H -=-∆+∆+ (9-8) 同理: ()B t A t t B t A t t V V g a H H --=-∆+∆+ (9-9) 方程(9-8)和(9-9)为水锤连锁方程。