方位角计算方法

方位角计算公式范文方位角是指从一个参考方向（通常是正北方向）起，按顺时针方向测量到其中一方向线的角度。

方位角通常用度数表示，范围从0度到360度。

下面介绍常见的方位角计算公式：1.方位角计算公式（两点坐标）：假设已知起点坐标A(x1,y1)和终点坐标B(x2,y2)，方位角θ的计算公式如下：θ = atan2(y2 - y1, x2 - x1)其中，atan2函数是一个双变量反正切函数，返回值为[-π, π]之间的角度值。

注意：上述公式计算得到的θ是以正北方向为参考的方位角。

如果要将方位角转换为以其他方向为参考的角度（如正东方向为0度），可以将θ减去相应的修正值。

2.方位角计算公式（两点经纬度）：假设已知起点的经度(lon1)、纬度(lat1)和终点的经度(lon2)、纬度(lat2)，方位角θ的计算公式如下：θ = atan2(sin(Δlon) * cos(lat2), cos(lat1) * sin(lat2) -sin(lat1) * cos(lat2) * cos(Δlon))其中，Δlon = lon2 - lon1是两点经度差。

注意：上述公式计算得到的θ是以正北方向为参考的方位角。

如果要将方位角转换为以其他方向为参考的角度（如正东方向为0度），可以将θ减去相应的修正值。

3.方位角计算公式（方向余弦矩阵）：方向余弦矩阵（Direction Cosine Matrix）是一种将方位角和俯仰角等转化为三维空间坐标旋转的方式。

方向余弦矩阵的计算公式如下：D=[ cos(θ) * cos(φ), sin(θ) * cos(φ), -sin(φ) ][ -sin(θ), cos(θ), 0 ][ cos(θ) * sin(φ), sin(θ) * sin(φ), cos(φ) ]其中，θ是方位角，φ是俯仰角。

D是一个3行3列的矩阵，表示坐标变换矩阵。

上述是常见的方位角计算公式，根据不同的应用场景和问题，可能还会有其他的计算公式。

一、直线定向1、正、反方位角换算对直线而言，过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角，而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角，同一条直线的正、反方位角相差，即同一直线的正反方位角＝ (1-13)上式右端，若<，用“＋”号，若，用“－”号。

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东（NE）、南东（SE）、南西(SW)、北西(NW)。

象限角和坐标方位角之间的换算公式列于表1-4。

表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限（NE）=第二象限（SE）=－第三象限（SW）=＋第四象限（NW）=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线（图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

设三点相关位置如图1-17()所示，应有＝＋＋ (1-14)设三点相关位置如图1-17()所示，应有＝＋＋－＝＋－ (1-15)若按折线前进方向将视为后边，视为前边，综合上二式即得相邻边坐标方位角推算的通式：＝＋(1-16)显然，如果测定的是和之间的前进方向右侧水平角，因为有＝－，代入上式即得通式＝－ (1-17)上二式右端，若前两项计算结果<，前面用“＋”号，否则前面用“－”号。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。

坐标,方位角计算公式坐标方位角=磁方位角+(±磁坐偏角)。

方位角是卫星接收天线，在水平面上转0°-360°。

设定方位角时，抛物面在水平面上左右移动。

方位角（方位角，缩写为Az）是用于测量平面中物体之间的角度差的方法之一。

它是从点的北方向顺时针方向和目标方向之间的水平角度。

一、计算方法1、按给定的坐标数据计算方位角αBA、αBPΔxBA=xA-xB=+123.461m；ΔyBA=yA-yB=+91.508m；由于ΔxBA>0，ΔyBA>0；可知αBA位于第Ⅰ象限，即αBA=arctg=36°32'43.64"；ΔxBP=xP-xB=-37.819m；ΔyBP=yP-yB=+9.048m；由于ΔxBP<0，ΔyBP>0；公式计算出来的方位角，可知αBP位于第Ⅱ象限。

αBP=180o-α=180o-arctg=180o-13o27'17.33"=166°32'42.67"；此外，当Δx<0，Δy<0；位于第Ⅲ象限，方位角=180°+arctg；当Δx>0，Δy<0；位于第Ⅳ象限，方位角=360°-arctg。

2、计算放样数据∠PBA、DBP∠PBA=αBP-αBA=129°59'59.03"。

3、测设时，把经纬仪安置在B点，瞄准A点，按顺时针方向测设∠PBA，得到BP方向，沿此方向测设水平距离DBP，就得到P点的平面位置。

当受地形限制不便于量距时，可采用角度交会法测设放样点平面位置上例中，当BP间量距受限时，通过计算测设∠PAB、∠PBA来定P点。

根据给定坐标计算∠PAB；ΔxAP=xP-xA=-161.28m；ΔyAP=yP-yA=-82.46m；αAP=180°+arctg=207°4'47.88"；又αAB=180°+αBA=180°+36°32'43.64"=216°32'43.64"；∠PAB=αAB-αAP=9°27'55.76"。

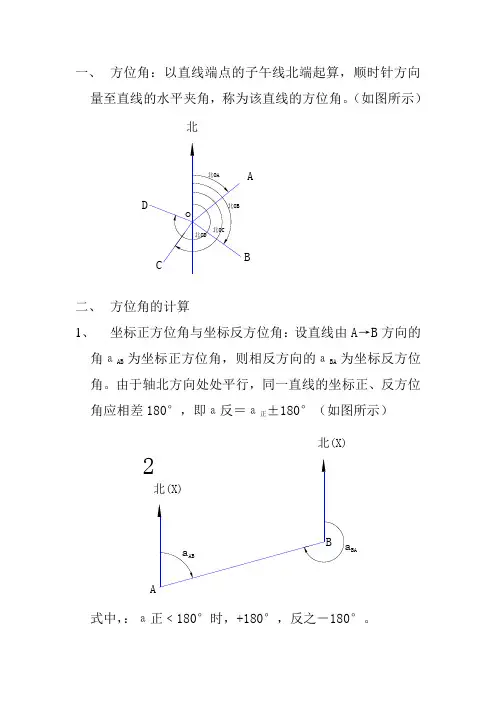
一、 方位角：以直线端点的子午线北端起算，顺时针方向量至直线的水平夹角，称为该直线的方位角。

（如图所示）
北
A
B
二、 方位角的计算
1、 坐标正方位角与坐标反方位角：设直线由A →B 方向的角аAB 为坐标正方位角，则相反方向的аBA 为坐标反方位角。

由于轴北方向处处平行，同一直线的坐标正、反方位角应相差180°，即а反＝а正±180°（如图所示）
2
北(X)
BA
式中，：а正﹤180°时，+180°，反之－180°。

2、两直线的坐标方位角аBA、аBC与水平夹角之间的关系：
（如图所示）
北(X)
A
①当β为ABC前进方向的右角时（顺时针），则
аBC＝аBA-β右
即计算式一：аBC＝аAB±180°-β右
②当β为ABC前进方向的左角时（逆时针），则
β右＝360°－β左
代入计算式一中，得计算式二：
аBC＝аAB±180°+β左
3、理解：前一边BC的坐标方位角等于后一边AB坐标方
位角加（或减）两边所夹的左（或右）角，再±180°。

4、注意：在计算过程中，当(а后+β左或а后－β右)﹤180°
时，用+180°；反之，－180°。

计算的结果大于360°应减去360°，为负值时应加360°。

工程测量中坐标方位角计算公式在工程测量中，坐标方位角是指一个点相对于参考方向的角度。

它是测量中常用的一个重要参数，用于确定物体或地点的位置和方向。

坐标方位角的计算公式主要基于三角函数的运算和几何原理，下面将详细介绍它的计算方法。

我们需要明确坐标方位角的定义。

在工程测量中，通常以正北方向为参考方向，以逆时针方向为正方向，来确定一个点的方位角。

方位角的范围是0°到360°，其中0°表示正北方向，90°表示正东方向，180°表示正南方向，270°表示正西方向，360°又回到正北方向。

对于任意一个点，我们可以通过计算该点相对于参考方向的角度来确定它的方位角。

具体的计算公式如下：方位角 = arctan((Y - Y0) / (X - X0))其中，X0和Y0表示参考点的坐标，X和Y表示待测点的坐标。

这个公式基于斜率的概念，通过计算两点之间的斜率来确定方位角。

需要注意的是，由于计算中使用了反正切函数arctan，所以计算结果的范围是-90°到90°，即仅限于第一象限和第四象限。

为了得到完整的方位角范围，我们需要进行一些额外的处理。

在计算公式中，我们可以根据X和X0的大小关系，以及Y和Y0的大小关系来确定方位角的象限。

具体的处理方法如下：如果X > X0且Y > Y0，那么方位角为计算结果；如果X < X0，那么方位角为180°加上计算结果；如果X > X0且Y < Y0，那么方位角为360°加上计算结果；如果X = X0且Y > Y0，那么方位角为90°；如果X = X0且Y < Y0，那么方位角为270°；如果X = X0且Y = Y0，那么方位角没有定义。

通过这些处理，我们可以得到完整的方位角范围。

在实际的工程测量中，坐标方位角的计算非常重要。

4
辅助 计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
－ 0.014
+8.350
－ 1.433
－ 0.005
－ 1.438
－ 2.745
－ 0.007
－ 2.752
+4.661
－ 0.008
+4.653
+ 8.847
－ 0.034
一、直线定向
1、正、反方位角换算
对直线
而言，过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角，而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角，同
一条直线的正、反方位角相差
，即同一直线的正反方位角
＝
(1-13>
上式右
端，若
<
，用“＋”号，若
，用“－”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上 所述，闭 合水准 路线的 计算方法除高差 闭合差 的计算有 所区别 而外，其余与附 合路线 的计算 完全相 同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例，已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3

方位角的计算方法：（已知方位角＋水平角大于540°－540°）已知方位角＋水平角±180°=方位角坐标增量的计算方法：平距×COS方位角=△X坐标增量平距×Sin方位角=△Y坐标增量坐标的计算方法：已知X坐标±△X坐标增量=X坐标已知Y坐标±△Y坐标增量=Y坐标高差、平距的计算方法：斜距×Sin倾角=高差斜距×COS倾角=平距高差÷Sin倾角=斜距平距÷cos已知度分秒=斜距高程的计算方法：已知高程－仪器高＋前视高±高差=该点的顶板高差原始记录计算方法：前视－后视相加÷2=水平角（前视不够－后视的＋360°再减）后视 00°00′00″ 180°00′09″前视92°49′02″272°49′13″水平角= 92°49′03″实测倾角：正镜－270°倒镜－90°（正、倒镜相加－360°）实例： 110°30′38″－90°= 00°30′38″实例： 270°30′38″－270°= 00°30′38″激光的计算方法：两点的高程相减：比如：5点高程1479、479－4点高程1471、052 = 8、427 两点之间的平距：60、673×tan7°19′25″=7、7988、427－7、797=0、629（上山前面的点一定高于后面的点，所以前面的点减后面的点）测量：1、先测后视水平角：归零，倒镜180°不能误差15′2、前视：先测水平角并读数记录，然后倒镜测倾角，水平角、平距、斜距、高差、量出仪器高，前视量出前视高。

要求方位角－已知方位角±180°=拨角方位画两千的图：展点用0.6正好.倾角的计算方法：180°以下的－90°270°－超过180°的两点的高差除平距按tan=倾角比如：2点1500、026－6点1484、096=15、932点～6点平距=127、8315、93÷127、83=接按第二功能键、接按tan接按=接按度分秒键完事。

坐标及方位角计算坐标和方位角是地理学和导航中常用的概念，用于确定一个地点在地球上的位置和方向。

坐标通常用经度和纬度表示，而方位角则是用于确定一个地点相对于另一个地点的方向。

在本文中，我们将介绍坐标和方位角的计算方法。

1.坐标的计算方法：坐标是用经度和纬度来表示一个地点在地球上的位置。

经度是指一个地点距离地球上子午线的距离，而纬度是指一个地点距离地球赤道的距离。

计算经度和纬度的方法如下：-经度的计算方法：经度的取值范围是从-180度到180度。

以本初子午线（通过伦敦的经线）为基准，向东为正，向西为负。

可以通过使用全球定位系统（GPS）或使用地图上的比例尺来确定一个地点的经度。

-纬度的计算方法：纬度的取值范围是从-90度到90度。

以地球赤道为基准，向北为正，向南为负。

可以通过使用全球定位系统（GPS）或使用地图上的比例尺来确定一个地点的纬度。

2.方位角的计算方法：方位角是用于确定一个地点相对于另一个地点的方向的角度。

方位角通常使用正北方向为基准，顺时针方向计算。

计算方位角的方法如下：-使用经纬度计算方位角：首先，计算两个地点的经度差和纬度差。

然后，使用三角函数（正弦、余弦或正切）计算两个地点之间的夹角。

最后，将夹角转换为以度为单位的方位角。

-使用几何图形计算方位角：将两个地点的经纬度绘制在一张地图上，并为两个地点之间的连线添加标记。

然后，使用直线夹角定理计算连线的夹角。

最后，使用罗盘或直尺等工具，将夹角转换为以度为单位的方位角。

总结：坐标和方位角是地理学和导航中常用的概念，用于确定一个地点在地球上的位置和方向。

坐标使用经度和纬度来表示一个地点的位置，而方位角用于确定一个地点相对于另一个地点的方向。

计算坐标和方位角的方法可以通过使用全球定位系统（GPS）、地图上的比例尺或几何图形等方法来进行。

测量学中坐标方位角计算公式在测量学中，坐标方位角是用于描述目标物体或点在水平坐标系中的方向的数值。

坐标方位角是指从北方向顺时针旋转到目标点所需的角度。

在实际的测量工作中，计算坐标方位角是非常重要的，它可以帮助测量员准确地确定目标点在地图上的位置。

计算公式计算坐标方位角的主要公式是使用三角函数来实现的。

具体的计算公式如下：方位角 = arctan((Y2 - Y1) / (X2 - X1))在上述公式中，X1和Y1表示起点的水平坐标值，X2和Y2表示终点的水平坐标值。

arctan表示反正切函数，它可以将斜率转化为角度值。

通过使用这个计算公式，我们可以得到起点和终点之间的坐标方位角。

需要注意的是，上述公式仅适用于计算水平平面上的坐标方位角。

如果需要在垂直平面上计算坐标方位角，我们还需要考虑高程的影响。

在这种情况下，计算公式会稍有不同，需要引入高程差的概念。

示例为了更好地理解坐标方位角的计算过程，我们可以通过一个示例来说明。

假设我们有两个点A和B，它们的水平坐标分别为：点A：(X1, Y1) = (100, 200)点B：(X2, Y2) = (150, 280)现在我们来计算点A和点B之间的坐标方位角。

首先，我们将点A和点B的坐标值代入计算公式中：方位角 = arctan((280 - 200) / (150 - 100))接下来，我们计算分子和分母的差值：方位角 = arctan(80 / 50)然后，我们计算这两个差值的比值：方位角 = arctan(1.6)最后，使用反正切函数来计算坐标方位角的数值：方位角≈ 56.31°所以，根据计算结果，点A和点B之间的坐标方位角约为56.31°。

结论测量学中的坐标方位角是用于描述目标物体或点在水平坐标系中方向的数值。

通过使用三角函数计算公式，我们可以准确地确定起点和终点之间的坐标方位角。

在计算时需要注意坐标值的顺序和差值的计算方法。

通过实际的计算示例，我们可以更好地理解和应用坐标方位角的计算公式。

根据两点坐标计算方位角方位角是指在平面直角坐标系中，以其中一固定点为起点，与水平轴正方向之间的夹角，一般用度数或弧度来表示。

计算两点之间的方位角可以使用三角函数的方法。

以两点A（x1,y1）和B（x2,y2）为例，我们可以将这两个点连接，并连接与x轴正方向之间的夹角，就是我们要计算的方位角。

步骤1：计算斜边的长度斜边的长度可以使用勾股定理来计算，公式为：AB = sqrt((x2 - x1)^2 + (y2 - y1)^2)步骤2：计算sin值sin值可以通过斜边与x轴正方向的夹角来计算，公式为：sinθ = (y2 - y1) / AB步骤3：计算cos值cos值可以通过斜边与y轴正方向的夹角来计算，公式为：cosθ = (x2 - x1) / AB使用反三角函数arcsin和arccos可以得到方位角的度数或弧度值：方位角= arcsin(sinθ) 或方位角= arccos(cosθ)需要注意的是，反三角函数的结果是一个范围在-π/2到π/2之间的角度，如果希望得到完整的方位角范围，还需考虑斜边所在的象限。

如果x2 > x1 且 y2 > y1，则得到的方位角为arcsin(sinθ)；如果x2 < x1 且 y2 > y1，则得到的方位角为180° -arcsin(sinθ)；如果x2 < x1 且 y2 < y1，则得到的方位角为180° +arccos(cosθ)；如果x2 > x1 且 y2 < y1，则得到的方位角为360° -arccos(cosθ)。

以下是一个用Python编写的示例代码，用于计算两点坐标之间的方位角：import mathdef calculate_bearing_angle(x1, y1, x2, y2):AB = math.sqrt((x2 - x1)**2 + (y2 - y1)**2)sin_theta = (y2 - y1) / ABcos_theta = (x2 - x1) / ABif x2 > x1 and y2 > y1:bearing = math.degrees(math.asin(sin_theta))elif x2 < x1 and y2 > y1:bearing = 180 - math.degrees(math.asin(sin_theta))elif x2 < x1 and y2 < y1:bearing = 180 + math.degrees(math.acos(cos_theta))elif x2 > x1 and y2 < y1:bearing = 360 - math.degrees(math.acos(cos_theta))return bearing#示例：x1=0y1=0x2=3y2=4bearing_angle = calculate_bearing_angle(x1, y1, x2, y2)print("方位角：", bearing_angle)方位角的计算方法可以应用于航海、航空、地理信息系统和导航等领域。

测量方位角计算公式测量方位角是指通过其中一种方法求得一些目标物体相对于指定基准方向的角度。

方位角通常使用度数表示，以正北方向为基准，沿顺时针方向递增，范围为0到360度。

测量方位角在地理导航、测量工程、天文学等领域有着广泛的应用。

计算方位角的公式主要有以下几种：1. 方位角 = atan((E - E0) / (N - N0))其中，E、N为目标物体的东北坐标，E0、N0为基准点的东北坐标。

该公式适用于平面坐标系。

2. 方位角 = atan2(E - E0, N - N0)其中，E、N为目标物体的东北坐标，E0、N0为基准点的东北坐标。

该公式适用于平面坐标系，可以通过atan2函数直接得到方位角，避免了先计算斜率再反求角度的过程。

3. 方位角= atan((sin(ΔL) * cos(L2)) / (cos(L1) * sin(L2) - sin(L1) * cos(L2) * cos(ΔL)))其中，ΔL为目标物体经度减去基准点经度的差值，L1、L2分别为目标物体和基准点的纬度。

该公式适用于地理坐标系。

4. 方位角= arc tan((sin(Δλ) * cos(φ2)) / (cos(φ1) *sin(φ2) - sin(φ1) * cos(φ2) * cos(Δλ)))其中，Δλ为目标物体经度减去基准点经度的差值，φ1、φ2分别为目标物体和基准点的纬度。

该公式适用于地理坐标系，常用于计算大地方位角。

这些公式的推导及原理比较复杂，涉及到三角学和二元一次方程等知识。

在实际应用中，可以通过使用现成的工具或软件来计算方位角，如地图软件、GPS定位设备等。

这些工具会自动计算目标物体相对于基准方向的角度，准确性高、方便快捷，可以满足大部分测量需要。

需要注意的是，测量方位角是基于特定坐标系的，不同坐标系的方位角计算公式可能有所不同。

另外，由于地球是一个球体，使用平面坐标系进行测量会引入一定的误差，尤其是在较长的距离范围内。

excel方位角计算公式方位角是指从北方向开始逆时针旋转到某个方向的角度。

在Excel中，可以通过一些数学函数和计算公式来计算方位角。

下面是一些相关参考内容，可以帮助你进行方位角计算。

1. 方位角的计算公式：方位角可以通过三角函数来计算，公式如下：方位角 = atan2(East, North)其中，East和North分别代表东方向和北方向的坐标轴上的值。

2. 利用Excel函数计算方位角：在Excel中，可以使用一些函数来计算方位角。

其中，atan2函数是可以直接计算方位角的函数。

在 Excel 中，可以使用以下公式计算方位角：方位角 = ATAN2(East, North)3. Excel中的ATAN2函数：ATAN2函数是Excel中的一个数学函数，用于计算给定点的方位角。

它接受两个参数：x和y。

ATAN2函数的返回值为[-π, π]的弧度值。

使用ATAN2函数计算方位角的示例：方位角 = ATAN2(East, North)其中，East和North分别是对应点的东方向和北方向的值。

4. Excel中的DEGREES函数：DEGREES函数用于将给定的弧度值转换为角度值。

在计算方位角时，通常会将通过ATAN2函数计算得到的弧度值转换为角度值。

使用DEGREES函数将弧度转换为角度的示例：角度值 = DEGREES(弧度值)5. Excel中的RADIAN函数：RADIAN函数用于将给定的角度值转换为弧度值。

在计算方位角时，通常需要将角度值转换为弧度值。

使用RADIAN函数将角度转换为弧度的示例：弧度值 = RADIAN(角度值)综上所述，可以通过在Excel中使用atan2函数、DEGREES 函数和RADIAN函数来计算方位角。

使用这些函数，可以方便地进行方位角的计算和转换。

方位角的计算方法方位角是指在平面直角坐标系中，特定点与正方向x轴之间逆时针方向的夹角。

它在数学、地理、航空航天等领域中都有广泛的应用。

计算方位角的方法主要有以下几种：1.基于直角坐标系的计算：假设有两个点A(x1, y1)和B(x2, y2)，首先需要计算出两点之间的直线斜率k = (y2 - y1) / (x2 - x1)。

然后利用反正切函数，通过求解arctan(k)得到弧度值θ。

最后利用单位换算，将弧度值θ转化为角度值α=θ * 180 / π，即为所求的方位角。

2.基于极坐标系的计算：在极坐标系中，一个点可以通过距离r和极角θ来表示。

假设有两个点A(r1,θ1)和B(r2,θ2)，要计算两点之间的方位角，首先需要将两点的极角θ转化为弧度制，然后通过计算Δθ=θ2-θ1得到两点之间的相对角度。

最后利用单位换算，将相对角度Δθ转化为角度值α=Δθ*180/π，即得到方位角。

3.基于方向向量的计算：假设有两个点A(x1, y1)和B(x2, y2)，可以将两点之间的连线看作一个方向向量。

首先需要计算出两点之间的方向向量V(x2 - x1, y2 - y1)。

然后利用反正切函数，通过求解arctan(Vy / Vx)得到弧度值θ。

最后利用单位换算，将弧度值θ转化为角度值α=θ * 180 / π，即为所求的方位角。

需要注意的是，在计算方位角时，可能会遇到特殊情况，例如：-当两点在同一直线上时，方位角为0或180度；-当两点重合时，方位角没有定义。

总结起来，方位角的计算方法有基于直角坐标系、极坐标系和方向向量三种方法，根据具体情况选择适合的方法进行计算。

计算细则1、坐标计算：X1=X+Dcosα,Y1=Y+Dsinα;式中 Y、X为已知坐标,D为两点之间的距离,Α为方位角;2、方位角计算：1、方位角=tan=两坐标增量的比值,然后用计算器按出他们的反三角函数±号判断象限;2、方位角：arctany2-y1/x2-x1;加减180大于180就减去180还大于360就在减去360、小于180就加180如果x轴坐标增量为负数,则结果加180°;如果为正数,则看y轴的坐标增量,如果Y轴上的结果为正,则算出来的结果就是两点间的方位角,如果为负值,加360°;S=√y2-y1+x2-x1,1)、当y2-y1>0,x2-x1>0时；α=arctany2-y1/x2-x1;2)、当y2-y1<0,x2-x1>0时；α=360°+arctany2-y1/x2-x1;3)、当x2-x1<0时；α=180°+arctany2-y1/x2-x1;再用两点之间的距离公式可算距离根号下两个坐标距离差的平方相加;拨角：arctany2-y1/x2-x11、例如：两条巷道要互相平行掘进的话,求它们的拨角：方法前视边方位角减后视边方位在此后视边方位要加减180°,若拨角结果为负值为左偏“逆时针”+360°就可化为右偏,正值为右偏“顺时针”;2、在图上标识方位的方法：就是导线边与Y轴的夹角;3、高程计算：目标高程=测点高程+h+仪器高—占标高;4、直角坐标与极坐标的换算：直角坐标用坐标增量表示；极坐标用方位角和边长表示1、坐标正算极坐标化为直角坐标已知一个点的坐标及该点至未知点的距离和方位角,计算未知点坐标方位角,知AXa,Ya、Sab、αab,求BXa,Ya解：Xab=Sab×COSαab 则有Xb=Xa+XabYab=Sab×SINαab Yb=Ya+Yab2)、坐标反算,已知两点的坐标,求两点的距离称反算边长和方位角称反算方位角的方法已知AXa,Ya、BXb,Yb,求αab、Sab;解：tanαab=Ya b/Xab所以;Αab=tanˉYab/Xab；则有：Sab=Yab/SINαab=Xab/COSαab=√X2ab+Y2ab;5、缘和曲线的方位角和坐标计算公式：S12=sqr<X2 -X12×Y2-Y12> =sqr X221× Y221;A12=arcsinY2-Y1/S12;S12为测站点1至放样点2的距离,A12为测站点1至放样点2的坐标方位角;X1,Y1为测站坐标,X2,Y2为放样点坐标;新公式：A12=arccosX21/S12×sgnY21360°只需将测量的成果用直线或其他线形连接起来;坐标输入时需注意交换输入,也就是将实测的X坐标在CAD中当Y坐标输入,而Y坐标则当X坐标输入;标高则用文字在标注在各相应的坐标点傍;一、建立新图时坐标偏移法1、先按比例大小绘制坐标网格,2、然后将测量整理得来的坐标拐点在CAD中输入绘制矿区范围,3、根据相应的测点坐标绘制实测图,4、填写图例;二、坐标增量上图相对坐标法①：如果比例尺为1:2000,平距除以2之后乘以方位角得坐标增量;②：点击直线或多线段按回车键点击后点,再输入ΔY,ΔX;倾斜巷道贯通计算：可根据倾斜角度进行换算,再结合地测交庄书中给的贯距或标高差来算,而且还要结合巷道的断面高差来综合计算;坡度的表示方法有百分比法、度数法、密位法和分数法四种;其中百分比法和度数法较为常用;1、百分比法表示坡度最为常用的方法,即两点的高程差与其水平距离的百分比,其计算公式如下：坡度=高程差/水平距离﹡100%,是指水平距离每100米垂直方向上下降…米;2、度数法用度数来表示坡度,利用反三角函数计算而得,其公式如下：TAN坡度=高程差 /水平距离,所以坡度=TAN-;一、平巷开门点仪器安设过程：用全站仪确定巷道开门点,C为开门点位置;1、在B点安置仪器,2、后视A点,用卷尺量出开门点的距离位置,定为C点然后在C点顶板钉点挂占标,再前视C点;3、把仪器移动安设在C点,后视B点,再用仪器把设计的方位、角度拨出来,用手拿着垂线或粉笔在开门点帮上,用仪器观测,左右移动垂线或粉笔,确定好准确点后用钉子钉上再用喷漆在帮上喷出;也就是中线点;为防止以后施工的破坏,多确定几个中线点,也是为了以后方便跟踪测量;一、标定腰线方法：1、用半圆仪标定倾斜巷道腰线,1点为新开斜巷的起点,称为起破点;1点高程H1由设计给出,Ha为已知点A高程,从图可知Ha-H1=ha在A点悬挂垂球,自A点向下量取ha,得到a点过a点拉一条水平线I'I,使1点位于新开巷道的一帮上,挂上半圆仪,此时半圆仪上读数应为0;将1点固定在巷道帮上,在1点系上测绳,沿巷道同侧拉向掘进方向,在帮上选定一点2,拉直测绳,悬挂半圆仪,上下移动测绳,使半圆仪的读数等于巷道设计倾角,此时固定2点,连接1、2点,划出腰线;2、用经纬仪标定腰线在主要倾斜巷道中,通常采用经纬仪标定腰线,其方法较多,这里只介绍三种; 1）、利用中线点标定腰线,图a为巷道横断图,图b为巷道纵断面图;标定方法如下：a：在中线点1安置仪器,量取仪器高i;b:使竖盘读数为巷道的设计倾角,此时的望远镜视线方向与腰线平行;然后瞄准掘进方向已标定的中线点2、3、4的垂线,分别作临时记号,得到 2'、3'、4',倒镜再测一次倾角a作为检查;c：由下式计算k值：k=H1-H'1+h-i;式中H1―1点处的高程；H'1 ―1点处轨面设计高程；i―仪器高；h ―轨面到腰线点的铅垂距离；d：由中线点的记号2'、3'、4' 分别向下量k值,得到 2"、3"、4"即为所求的腰线点;e：用半圆仪分别从腰线点拉一条垂直中线的水平线到两帮上;f：用测绳连接帮壁上的2"、3"、4"点并用喷漆沿测绳划出腰线;3、平巷与斜巷连接处腰线的标定：平巷与斜巷连接处是巷道坡度变化的地方,腰线到这里要改变坡度,巷道底板在竖起面上的转折点称为巷道变坡点,设平巷腰线到轨面或底板的距离为a,斜巷腰线到轨面或底板的法线距离也保持为a,那么,在变坡点处,平巷腰线必须抬高Δh,才能得到斜巷腰线起坡点,或者自变坡点处向前或向后量取距离ΔL,得到斜巷腰线起坡点,由此标定出斜巷腰线; Δh和ΔL值按下式计算Δh=a/COSδ-a=asecδ-1ΔL= Δδ;标定时,测量人员首先应在平巷的中线点上标定出A点的位置,然后在A点垂直于巷道中线的两帮上标出平巷腰线点,再从平巷腰线向上量取Δh 也可向前或向后量取ΔL,得到斜巷腰线起坡点位置;斜巷掘进时的最初10米,可以用半圆仪在帮手按δ角划出腰线;倾斜巷道的贯通：上下平巷和一号下山已掘好,二号下山正由下向上开掘至B点,现为加快掘进速度,欲上下同时开掘;这种贯通的特殊性在于上部开切点P的位置是未知的;为此,首先应确定P点的位置;确定P点的位置的方法主要有两种：第一种是根据A和C、B和D的坐标,列出直线方程,求解出交点P的位置;这种方法解联立方程的工作相当复杂,一般不予采用;第二种方法是根据三角学的基本知识,解算ΔAPB;由于在ΔAPB中,A、B的坐标已知,从而可求出它们间的水平距离Lba,和方位角eab,而且eba=edb,eap=eac也是已知的;这样我们就可以根据正弦定理求得Lap,确定出P点的位置;Lap=LbaSINδb/SINδp=<Ya-YbCOSeb-Xa-XbSINedb>/SINebd-eca;P点确定后,即可测定出其高程Hp,然后即可按与第一个例子类似的方法,标定贯通巷道的中线和腰线;水平巷道间的贯通：1、准备工作布设仪器和水准路线,计算出A、B点的平面直角坐标XA,YA、XB,YB以及它们的高程Ha、Hb;2、计算贯通测量的几何要素1计算贯通巷道中心线的方位角aAB:tanaAB=YB-YA/XB-XA;（2）计算A、B处的指向角β1、β2：β1=αAB- αAC β2=αBA- αBD(3)计算A、B间的水平距离LAB:LAB=√XB-XA2+YB-YA2;（4）计算贯通巷道的倾角δ：tanδ=HB-HA/LAB;（5）计算A、B间的斜长LAB：LAB=√LAB2+HB2-HA2或LAB=LAB/COSδ。

日出方位角计算公式日出方位角计算公式：日出方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]；公式中,M-某天太阳直射的纬度,N-某地的纬度,^2-平方。

太阳方位角计算公式：太阳高度角hs：sinhs=sinφ·sinδ+cosψ·cosδ·cosΩ；式中 hs-太阳高度角、φ-地理纬度、δ-赤纬、Ω-时角。

太阳方位角As：COSAs= sinhs·sinψ-sinδ/(coshs·cosψ)；式中As-太阳方位角。

太阳高角度：太阳高度角是从观测者所在地和太阳中心的联线与地平面所夹的角度。

天顶角是是高度角的余角，也就是(90°–gS )。

当太阳的高度角为90°，即太阳位于天顶，因此太阳的天顶角为0。

日地距离计算公式：ER=1.000423+0.032359sinθ+0.000086sin2θ-0.008349cosθ+0.000115cos2θ；式中θ称日角，即θ=2πt/365.2422。

太阳方位角的测定方法：对于中国区域，早上太阳光从东边射来，中午太阳光从南边射来，傍晚太阳光从西边边射来，早上的太阳方位角在90°左右(但一年当中，有一定的角度范围变化)，正中午的太阳方位角在180°(正南方)，傍晚的太阳方位角在270°左右(但一年当中，有一定的角度范围变化)。

例如北京处在北纬约40°，一年中，早上的太阳方位角变化量约为90°±31°；对于陆地卫星系统而言，如美国的Landsat TM/ETM+，该卫星的过境(中国)时间大概是早上到中午之间，因此其太阳方位角一般在0°和90°之间；对于地球上任何位置，当太阳处于春分点或秋分点，即太阳赤纬是0°的时候，初升的太阳方位角是90°整，正午太阳方位角是180°，落日的时候太阳方位角是270°；对北半球而言，当太阳赤纬大于0°的时候太阳从东偏北方向升起，此时太阳方位角小于90°，中午180°，落日时太阳方位角大于270°。

方位角计算详细方法方位角是指物体相对于观察者的方向。

在地理学和航海学中，方位角通常用于描述一点相对于北方的方向。

在天文学中，方位角通常用于描述一个天体相对于天球上的其他天体或地平线的方向。

在航海学中，方位角通常使用360度制表示，其中0度表示北方，90度表示东方，180度表示南方，270度表示西方。

在天文学中，方位角通常使用360度制或24小时制，其中0度或0小时表示地平线上的点，90度或6小时表示东方的点，180度或12小时表示南方的点，270度或18小时表示西方的点。

方位角的计算通常涉及到三个参数：观察者的位置、目标物体的位置和参考方向。

下面是方位角计算的详细方法：1.确定观察者的位置：方位角的计算需要知道观察者的经度和纬度坐标。

这可以通过使用全球定位系统（GPS）或地图上的经纬度线来确定。

2.确定目标物体的位置：类似地，需要知道目标物体的经度和纬度坐标。

这可以通过使用GPS或地图来确定。

3.确定参考方向：方位角的计算需要一个参考方向作为起点。

这可以是北方、南方、东方或西方。

通常情况下，北方被选为参考方向，其中北方的方位角为0度（360度制）或0小时（24小时制）。

4.计算目标物体相对于观察者的经度差和纬度差：将目标物体的经度减去观察者的经度，得到经度差。

将目标物体的纬度减去观察者的纬度，得到纬度差。

5.计算方位角：使用三角函数（如正切函数）计算经度差和纬度差的比值。

根据参考方向的选择，可以使用不同的计算公式。

以下是一些常用的计算公式：- 如果参考方向是北方，则方位角可以通过以下公式计算：方位角 = arctan（经度差/纬度差）。

- 如果参考方向是南方，则方位角可以通过以下公式计算：方位角 = 180度 - arctan（经度差/纬度差）。

- 如果参考方向是东方，则方位角可以通过以下公式计算：方位角 = 90度 - arctan（纬度差/经度差）。

- 如果参考方向是西方，则方位角可以通过以下公式计算：方位角 = 270度 + arctan（纬度差/经度差）。

测量坐标方位角计算公式是什么引言在测量和导航领域中，确定两个点之间的方位角（也称为方向角或航向角）是一项重要的任务。

方位角定义为从一个参考点到目标点的方向，通常以北方向为参考。

测量坐标方位角是一种基本的导航技术，广泛应用于地理测量、航行、航空、地图制作等领域。

本文将介绍如何计算测量坐标方位角的公式。

问题陈述给定两个点的坐标（经度和纬度），我们的目标是计算从一个点到另一个点的方位角。

方法为了计算两个点之间的方位角，我们可以使用以下公式：Δφ = φ2 - φ1Δλ = λ2 - λ1θ = atan2(sin(Δλ) * cos(φ2), cos(φ1) * sin(φ2) - sin(φ1) * cos(φ2) * co s(Δλ))其中，φ1和λ1是起始点的纬度和经度，φ2和λ2是目标点的纬度和经度。

Δφ和Δλ是纬度和经度的差值。

以上公式是基于球面三角学的原理。

测量坐标方位角的计算方法是通过计算两个点形成的三角形的角度来确定方位角。

理解公式让我们逐步分解公式来理解其含义。

首先，我们计算纬度差值Δφ和经度差值Δλ。

这是因为方位角的计算涉及到两个点之间的相对位置。

接下来，我们使用以下公式计算方位角θ：•sin(Δλ) * cos(φ2)：这部分表示纬度差（即起始点到目标点的维度变化）对方位角的影响。

sin(Δλ)表示纬度差的正弦值，而cos(φ2)表示目标点纬度的余弦值。

•cos(φ1) * sin(φ2) - sin(φ1) * cos(φ2) * cos(Δλ)：这部分表示经度差（即起始点到目标点的经度变化）对方位角的影响。

cos(φ1) *sin(φ2)表示起始点纬度的余弦值乘以目标点纬度的正弦值，而sin(φ1) *cos(φ2) * cos(Δλ)表示起始点纬度的正弦值乘以目标点纬度的余弦值再乘以经度差的余弦值。

最后，使用atan2()函数计算弧度，并将其转换为角度值。

结论本文介绍了计算测量坐标方位角的公式。