6.受压构件承载力计算(6.4-6.6)解析
- 格式:ppt
- 大小:1.61 MB
- 文档页数:76


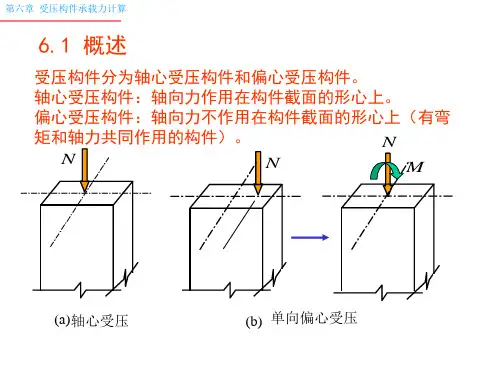
受压构件的承载力计算一、梁柱的承载力计算方法对于受压构件,在弹性范围内,可以采用弹性承载力计算方法。
弹性承载力计算方法是根据梁柱的理论,主要应用弹性力学原理和应变能平衡条件进行计算。
在弹性承载力计算之外,受压梁柱的承载力还受到稳定性要求的限制。
稳定性要求主要包括屈曲的要求和稳定的要求。
稳定性承载力计算方法就是根据稳定性要求来计算的。
二、承载力计算的基本原理和方法1.构件的截面形态与材料的力学性能有关。
几何形态方面,可以通过截面形心深度、截面形态系数和截面面积等参数来描述。
力学性能方面,主要包括材料的抗压强度、屈服强度和弹性模量等参数。
2.构件的边界条件与受力特性有关。
边界条件主要包括自由端的约束、内力的约束和约束条件等。
边界条件对构件的承载力有着直接的影响,需要进行准确的分析和计算。
3.构件的荷载和荷载组合也是影响承载力计算的重要因素。
荷载包括静力荷载和动力荷载,荷载组合则是不同荷载的叠加组合。
需要根据具体情况来确定荷载和荷载组合,并进行相应的计算。
假设一个矩形柱的尺寸为300mm×400mm,材料抗压强度为250MPa,弹性模量为200 GPa。
根据以上参数,可以进行如下步骤的承载力计算。
1.计算截面形态参数:矩形柱的形心深度h=400/2=200mm形态系数α=(h/t)f/π^2=2.692.弹性承载力计算:根据梁柱的理论,弹性承载力可通过以下公式计算:Pcr=(π^2*E*I)/(kl)^2其中,E为弹性模量,I为惯性矩,kl为有效长度系数。
惯性矩I=1/12*b*h^3=1/12*300*400^3=32,000,000mm^4有效长度系数kl可根据梁柱的边界条件和约束情况进行计算。
假设矩形柱两端均固定,则kl=0.5代入以上参数,可以得到弹性承载力Pcr=200,000N=200kN。
3.稳定性承载力计算:稳定性承载力计算主要包括屈曲的要求和稳定的要求。
对于矩形柱,屈曲要求可通过欧拉公式计算,稳定的要求可通过查表确定。



06受压构件承载力计算随着工程领域应用的不断深入,受压构件的承载力计算也变得越来越重要。
受压构件是指在受到外力作用下,以抵抗压力为主要承载形式的构件,如柱、墙、梁等。
本文将介绍关于受压构件承载力计算的基本原则和方法。
首先,受压构件承载力计算的基本原理是根据构件的几何形状、材料特性以及外力情况来确定构件能够承受的最大压力。
在计算过程中,一般会考虑构件的屈服强度、稳定性以及整体的平衡状态。
其次,受压构件的承载力计算方法主要有弯曲屈服强度法、稳定屈服强度法和极限承载力法等。
弯曲屈服强度法是基于构件受压时的挠度和变形来计算承载力的一种方法。
该方法主要考虑构件在受压时的弯曲和屈曲现象,通过应变-应力关系和变形-受力关系来计算构件的承载力。
这种方法适用于承受轴向压力作用下的细长构件,如柱、墙等。
稳定屈服强度法是基于构件受压时的稳定性和屈服强度来计算承载力的一种方法。
该方法主要考虑构件受压时的稳定性问题,如整体变形和局部失稳等。
通过分析和求解构件的稳定性方程来计算构件的承载力。
这种方法适用于承受轴向压力作用下的短柱、框架结构等。
极限承载力法是基于构件受压时的极限承载力来计算承载力的一种方法。
该方法主要考虑构件在受压时的破坏模式和破坏机理,通过分析构件的极限承载力来计算其承载力。
这种方法适用于承受轴向压力作用下的混凝土构件、钢结构等。
在实际工程中,根据具体情况选择适当的计算方法非常重要。
且在计算过程中需要考虑一些约束条件,如构件的几何尺寸、材料特性、外力作用、边界条件等。
同时还需要对构件的安全系数进行合理设置,以保证构件在承受压力时的安全性。
综上所述,受压构件承载力计算涉及到多个因素,包括构件的几何形状、材料特性以及外力情况等。
通过合理选择计算方法,考虑约束条件和安全系数,可以准确计算出受压构件的承载力,为工程实践提供重要的指导依据。




6受压构件承载力计算受压构件是指在受外部加载作用下,构件内部会发生挤压应力的构件。
在建筑设计中,受压构件的承载力计算是十分重要的,因为它直接关系到构件的安全性和可靠性。
本文将介绍受压构件的承载力计算方法,并通过一个具体的例子进行详细说明。
受压构件的承载力计算一般包括两种情况:稳定受压构件和不稳定受压构件。
稳定受压构件是指构件在受到外部加载后,构件内部只产生一种挤压应力,不会引起构件的屈曲和不稳定破坏。
而不稳定受压构件是指在外部加载作用下,构件可能会发生屈曲和不稳定破坏。
因此,在受压构件的设计中,需要考虑构件的稳定性和承载力。
首先,我们来看稳定受压构件的承载力计算方法。
稳定受压构件的承载力可以通过公式计算:\[P_{cr} = \dfrac{\pi^2 E I}{(KL)^2}\]其中,\(P_{cr}\)为稳定受压构件的临界荷载,\(E\)为构件的杨氏模量,\(I\)为构件的惯性矩,\(K\)为构件的端部系数,\(L\)为构件的长度。
具体来说,如果我们要计算一个钢筋混凝土柱的承载力,可以根据柱的截面形状和材料性质计算出惯性矩\(I\)和杨氏模量\(E\),然后确定柱的端部系数\(K\)和长度\(L\),最后可以根据上述公式计算出柱的稳定受压承载力。
接下来,我们来看不稳定受压构件的承载力计算方法。
不稳定受压构件的承载力一般通过欧拉公式计算:\[P_{cr} = \dfrac{\pi^2 E I}{(kL)^2}\]其中,\(P_{cr}\)为不稳定受压构件的临界荷载,\(E\)为构件的杨氏模量,\(I\)为构件的惯性矩,\(k\)为构件的有效长度系数,\(L\)为构件的长度。
不稳定受压构件的承载力计算需要考虑构件的有效长度系数\(k\),有效长度系数与构件的支座约束条件有关。
一般来说,当构件两端都固定支座时,有效长度系数为1;当构件一端固定支座一端可转动支座时,有效长度系数为2;当构件两端都可转动支座时,有效长度系数为4通过以上介绍,我们可以看到受压构件的承载力计算是十分复杂的,需要考虑构件的材料性质、截面形状、长度、支座约束条件等因素。
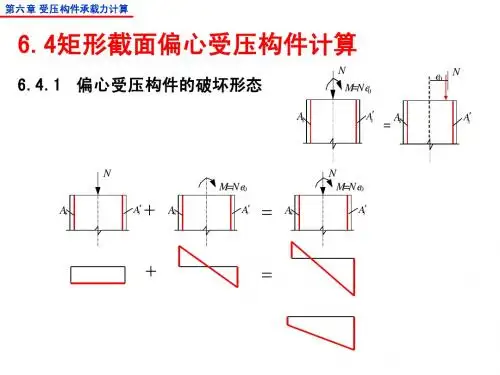
6受压构件承载力计算受压构件承载力计算是结构设计中一个重要的环节,通过对材料的性能和结构的几何形状进行分析,确定结构承受压力的能力。
本文将以混凝土柱为例,介绍受压构件承载力计算的步骤和相关公式。
首先,需要明确受压构件的几何形状和材料的性能参数。
混凝土柱常见的几何形状有方形、圆形和矩形等,不同的形状对应着不同的计算公式。
同时,混凝土的性能参数包括抗压强度、弹性模量和受压构件的尺寸等。
其次,需要确定受压构件的屈服状态。
混凝土受压构件的屈服状态可以分为两种情况:混凝土全面屈服和钢筋屈服。
混凝土全面屈服时,受压构件的承载力由混凝土的抗压强度决定;钢筋屈服时,受压构件的承载力由钢筋的抗拉强度决定。
在混凝土全面屈服情况下,受压构件的承载力计算可以通过极限平衡原理得到。
混凝土柱的承载力可以表示为:P = 0.85 * fcb * Ac + As * fs其中,P为受压构件的承载力,0.85为抗压强度折减系数,fcb为混凝土的抗压强度,Ac为受压构件的截面积,As为受压构件内的钢筋面积,fs为钢筋的抗拉强度。
需要注意的是,在计算混凝土柱的承载力时,应考虑混凝土开裂后的受压区失效。
为了满足混凝土柱的延性要求,通常采用受压钢筋和箍筋束进行加固,并计算加固后的承载力。
在加勒式轴心受压构件中,受压钢筋抵抗混凝土开裂是非常重要的。
在钢筋屈服情况下,受压构件的承载力主要由钢筋的抗拉强度决定。
P = As * fs其中,As为受压构件内的钢筋面积,fs为钢筋的抗拉强度。
最后,我们需要对计算结果进行验证和修正。
通过计算得到的承载力与结构的实际要求进行比较,以确定设计方案的可行性。
如果计算结果超过了结构的要求,需要进行结构的优化和调整。
综上所述,受压构件的承载力计算是结构设计中的重要环节。
通过确定受压构件的几何形状和材料性能参数,然后根据受压构件的屈服状态选择对应的计算公式,最后验证和修正计算结果,可以得到一个符合实际要求的结构设计方案。