正方体的11种展开图(描点,描线含练习题)

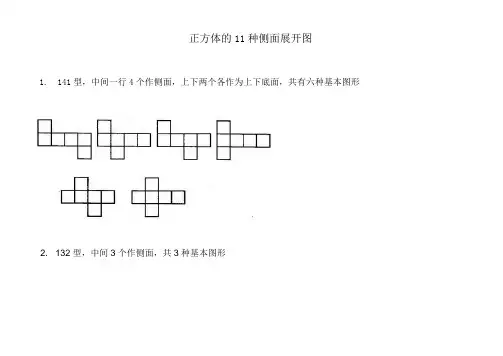
正方体的11种侧面展开图
1. 141型，中间一行4个作侧面，上下两个各作为上下底面，共有六种基本图形
2. 132型，中间3个作侧面，共3种基本图形
3. 222型，两行只能有1个正方形相连
4. 33型，两行只能有一个正方形相连
小结：一四一，都可以；
一三二,二必连；
二成三阶梯；
两排三三连；
田字必舍弃。

正方体的展开图可以按照行进行分类。

主要有以下特点：
1.上中下三行，每两行之间只能有一条边重合。

2.222、33两类是特殊的，为阶梯状。

3.有的看似不属于任一类，旋转后就是其中一类了。

在下面的口诀中，前四行是描述十一种展示图的特点，后两行是描述哪些图形不能构成正方体，哪些面是相对的面，哪些面是相邻的面。

正方体展开图口诀
正方体展有规律，十一种类看仔细；
中间四个成一行，两边各一无规矩；
二三紧连错一个，三一相连一随意；
两两相连各错一，三个两排一对齐。

一条线上不过四，田七和凹要放弃；
相间之端是对面，间二拐角面相邻。

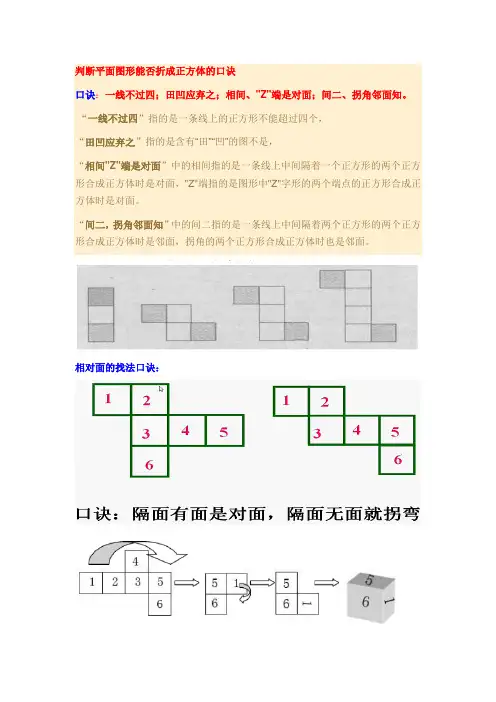
判断平面图形能否折成正方体的口诀口诀：一线不过四；田凹应弃之；相间、"Z"端是对面；间二、拐角邻面知。

“一线不过四”指的是一条线上的正方形不能超过四个，“田凹应弃之”指的是含有“田”“凹”的图不是，“相间"Z"端是对面”中的相间指的是一条线上中间隔着一个正方形的两个正方形合成正方体时是对面，"Z"端指的是图形中"Z"字形的两个端点的正方形合成正方体时是对面。

“间二，拐角邻面知”中的间二指的是一条线上中间隔着两个正方形的两个正方形合成正方体时是邻面，拐角的两个正方形合成正方体时也是邻面。

相对面的找法口诀：第18讲 图形推理-空间重构类-描点法（图形）（流畅）.f4v答案：B 答案：D。

答案：A。

答案：B 答案：C答案：B。

答案：C。

【例题1】（2012年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：由以上性质可以可以看出，一点面和四点面为对立面，B项错误；C项中一点面与六点面构成如图相邻关系时，五点面应位于左面而右顶面（可以六点面为上面折叠），排除；二点面、三点面、四点面三面相邻，且公共顶点不变，三点面方向不对，D项错误。

注：平面图形的公共顶点和公共边折叠成多面体后仍为这三个面的公共顶点和公共边。

（通过上图D项可验证）【例题2】（2010年国家）左边给定的是纸盒的外表面，下面哪一项能由它所折叠而成（）一本通解答：横线面和空白面为对立面，C、D项错误；B项中右面及上面的两条线错误，排除。

【例题3】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？一本通解答：A项三条斜线不可能交于一点，排除。

C项两条水平线不会交于一点，排除。

D项正面应为竖直线，排除。

【例题4】（2008年江苏B类）一本通解答：B。

解法一：三个空白面都不相互对立，是相邻的，B项正确。

解法二：三条对角线不会交于一点，也不会首尾相连，排除C、D两项；前表面和右表面的线段交点应该是在下方，排除A项，所以B项正确。

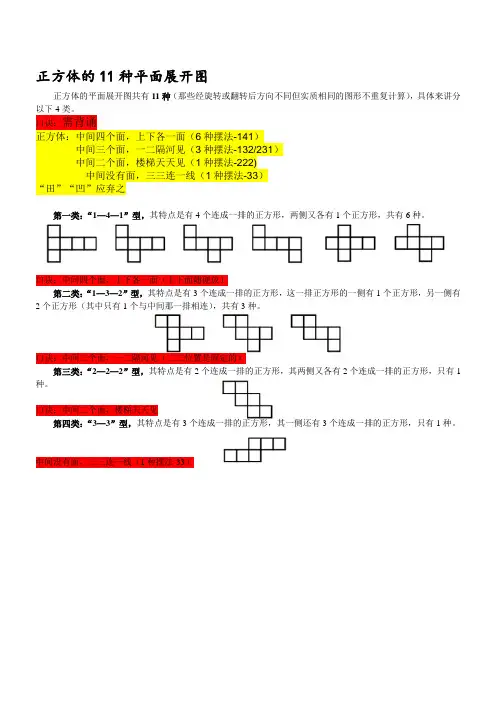
正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体的11种平面睁开图之杨若古兰创作正方体的平面睁开图共有11种（那些经扭转或翻转后方向分歧但实质不异的图形不反复计算），具体来讲分以下4类.
口诀：需背诵
正方体：两头四个面，上下各一面（6种摆法-141）
两头三个面，一二隔河见（3种摆法-132/231）
两头二个面，楼梯天天见（1种摆法-222)
两头没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种.
口诀：两头四个面，上下各一面（上上面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只要1个与两头那一排相连），共有3种.
口诀：两头三个面，一二隔河见（二三地位是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只要1种.
口诀：两头二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只要1种.
两头没有面，三三连一线（1种摆法-33）。

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

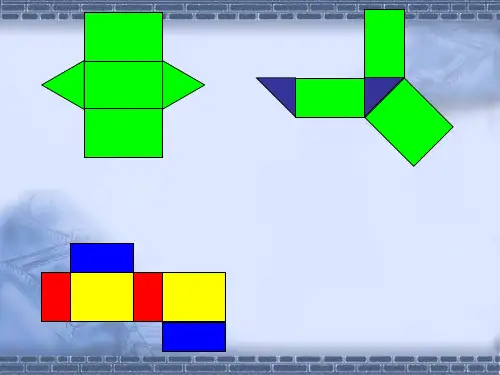
正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

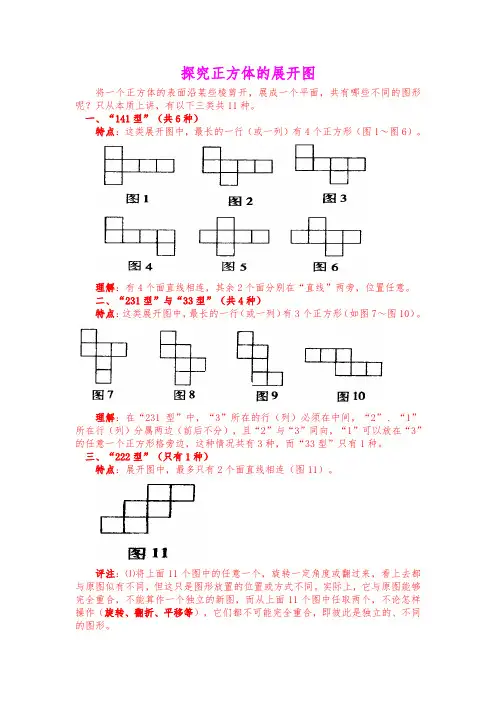
探究正方体的展开图
将一个正方体的表面沿某些棱剪开，展成一个平面，共有哪些不同的图形呢？只从本质上讲，有以下三类共11种。

一、“141型”（共6种）
特点：这类展开图中，最长的一行（或一列）有4个正方形（图1～图6）。

理解：有4个面直线相连，其余2个面分别在“直线”两旁，位置任意。

二、“231型”与“33型”（共4种）
特点：这类展开图中，最长的一行（或一列）有3个正方形（如图7～图10）。

理解：在“231型”中，“3”所在的行（列）必须在中间，“2”、“1”所在行（列）分属两边（前后不分），且“2”与“3”同向，“1”可以放在“3”的任意一个正方形格旁边，这种情况共有3种，而“33型”只有1种。

三、“222型”（只有1种）
特点：展开图中，最多只有2个面直线相连（图11）。

评注：⑴将上面11个图中的任意一个，旋转一定角度或翻过来，看上去都与原图似有不同，但这只是图形放置的位置或方式不同。

实际上，它与原图能够完全重合，不能算作一个独立的新图，而从上面11个图中任取两个，不论怎样操作（旋转、翻折、平移等），它们都不可能完全重合，即彼此是独立的、不同的图形。

⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图，如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型，就一定不能折成正方体。

概括地说，只要不符合上述“141”、“231”和“33”、“222”的特点，就不能折成正方体。

如图12，如果将其看作“231”型，那么，无论怎么看，“2”和“3”都不是同向，故不能折成正方体。

其实，它属于“123”（或“321”）型。