【计算机科学】_正交分解_期刊发文热词逐年推荐_20140727
- 格式:xls
- 大小:90.04 KB
- 文档页数:80

正交分解法——把力沿着两个经选定的互相垂直的方向分解,其目的是便于运用普通代数运算公式来解决矢量运算。
利用力的正交分解法求合力:这是一种比较简便的求合力的方法,它实际上是利用了力的分解的原理把力都分解到两个互相垂直的方向上,然后就变成了在同一直线上的力的合成问题了.这样计算起来就简单多了。
力的正交分解法步骤如下:1、正确选定直角坐标系:通常选共点力的作用点为坐标原点,坐标轴的方向的选择则应根据实际问题来确定。
原则是使坐标轴与尽可能多的力重合,即是使需要向两坐标轴投影分解的力尽可能少,在处理静力学问题时,通常选用水平方向和竖直方向上的直角坐标,当然在其它方向较简便时,也可选用。
一般选水平和竖直方向上的直角坐标;也可以选沿运动方向和垂直运动方向上的直角坐标.在力学计算上,这两种选择可以使力的计算最简单,只要计算到互相垂直的两个方向就可以了,不必求总合力.2、分别将各个力投影到坐标轴上:分别求x轴和y轴上各力的投影的合力和其中:(式中的轴上的两个分量,其余类推。
)这样,共点力的合力大小可由公式:求出。
设力的方向与轴正方向之间夹角是。
∴通过数学用表可知数值。
注意:如果这是处理多个力作用下物体平衡问题的好办法。
计算方法举例:例:如图所示,物体A在倾角为θ的斜面上匀速下滑,求物体受到的摩擦力及动摩擦因数。
分析:选A为研究对象分析A受力作受力图如图,选坐标如图:将不在坐标轴上的重力在x,y坐标上分解:Gx=GžsinθGy=Gžcosθf在x轴(反向),N在y轴上(正向)∵物体匀速下滑则有则一、合力与分力:在实际问题中,一个物体往往同时受到几个力的作用。
如果一个力产生的效果与原来几个力产生的效果相同,这个力就叫那几个力的合力,而那几个力就叫这个力的分力。
二、力的合成与分解:求几个力的合力的过程叫力的合成,求一个力的分力的过程叫力的分解。
合力与分力有等效性与可替代性。
求力的合成的过程实际上就是寻找一个与几个力等效的力的过程;求力的分解的过程,实际上是寻找几个与这个力等效的力的过程。

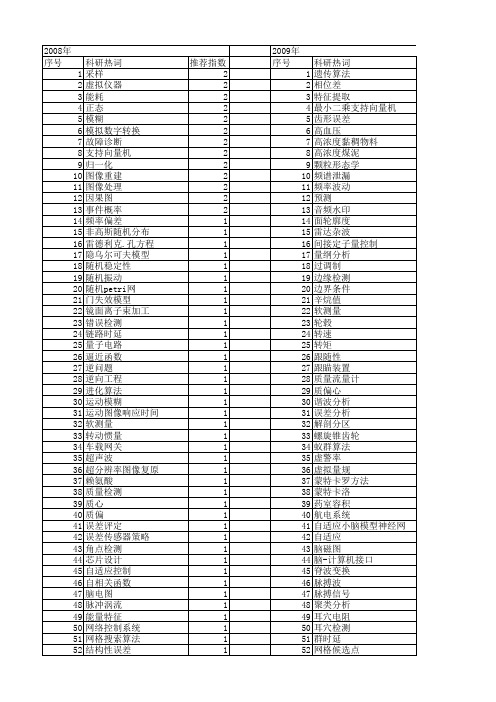

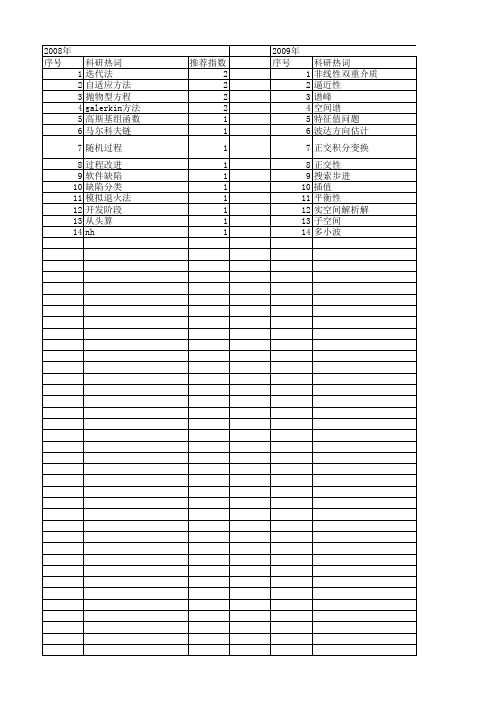
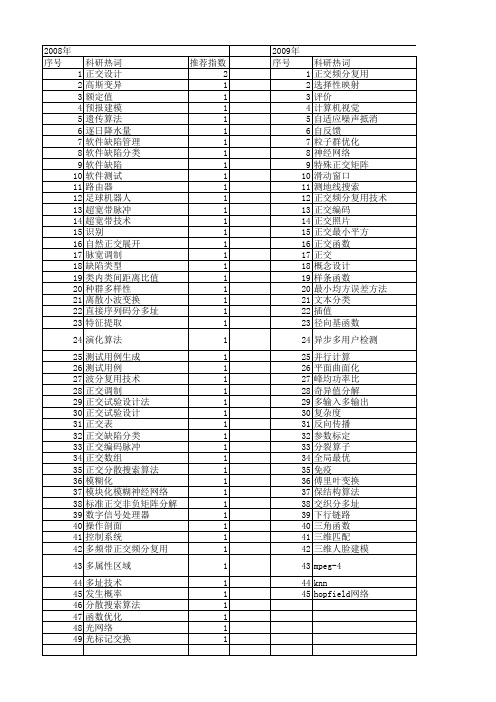
介绍正交分解法
正交分解法(Orthogonal Decomposition)是一种多元分析方法,它将观测样本投射到以主成分分析(Principal Component Analysis,PCA)为基础的一组正交变
量上面,从而实现对观测样本的模式和结构的分析。
正交分解法的最大优势在于,它不仅能够发掘潜在变量之间存在的偏序关系,还能够明确表达出正负关联关系,而此类信息在多元分析方法中并不容易被慢慢挖掘。
正交分解法可以利用被观测样本权重构建(weighted reconstructent)来实现对
不同变量之间关系的研究;另外,正交分解还能够模拟多元变量模型以及降维手段,进而研究不同变量之间的分类角色。
相对于PCA,正交分解法还可以研究复杂业
务流程中不同行动的顺序规律及关联,明确识别变量之间的线性以及负相关性。
正交分解法是一种兼具多元统计分析和统模建模能力的综合方法,它可以从有限观测样本中提取出大量真实变量之间的关系,进而帮助研究者分析出各个变量究竟说一起运作,这大大提高了变量之间关联性分析的效果和准确性,以满足各个研究领域实战需求。
介绍正交分解法
正交分解法(OrthogonalDecomposition)是计算机科学中一种重要的数学方法,它可以用来解决复杂的数学问题,以及实现机器学习算法。
它可以将一份计算任务分解成一系列独立的子任务,这些子任务可以同时进行,或者也可以顺序进行。
正交分解法可以在多核处理器、并行编程、数据库系统等多个领域上都有所应用。
在数学上,正交分解法也被称作“线性分解”。
它是一种数学技术,可以将复杂的函数表示为基于多个简单的子函数的线性组合。
它的典型应用是,将一个多元函数拆分成它的线性组合成分,并以这种方式解决复杂的数学问题。
从多核处理器的角度来说,正交分解法可以用来同时运行多个线程。
这样可以分发任务,从而提高系统效率。
此外,正交分解法也可以用来实现高级的机器学习技术,如神经网络和支持向量机,从而提高系统的预测能力和准确性。
正交分解法可以用来构建高效的数据库索引,例如B树和红黑树等。
它的基本原理是,将数据库中的数据划分成不同的分区,每个分区放置在不同的数据库表中,从而有效地提高查询速度。
正交分解法有很多应用,它可以用来实现多核处理器、并行编程、机器学习算法、数据库索引等。
它主要的优点是拆分复杂的任务,从而提高CPU利用率,提高系统性能。
它主要的缺点也是非常明显的:由于它只能针对线性问题进行分解,无法解决非线性问题,因此在某些复杂的问题上表现不够理想。
总之,正交分解法是一种重要的数学方法,可以用来改善系统性能,提高多核处理器效率,实现机器学习算法,以及构建高效的数据库索引。
但是,它只能解决线性问题,无法解决非线性问题,因此其应用仍然有限。
介绍正交分解正交分解是一项有效的数理统计方法,它可以帮助我们分析复杂的信息系统,发现隐藏的联系和结构。
它可以用来探索数据本身的信息,揭示其内在结构,从而有助于更好地理解数据的本质。
在最近的几十年中,正交分解的应用越来越广泛,它为科学研究,业务决策和许多其他领域提供了有价值的信息。
正交分解是一种数学分析技术,它可以用来研究具有相关性的多变量数据。
它利用一组互相正交的基底向量来捕捉数据中存在的强关联性,有助于减少数据中的噪声,提取有用信息。
正交分解的目的是从含有相关性的多变量数据中获得有意义的结构,比如统计信息,数据聚类或数据分布。
正交分解可以包括多种不同的技术,比如主成分分析(PCA),独立分量分析(ICA)和因子分析(FA)。
这些方法都利用了正交分解的基本概念,并以不同的方式实现。
主成分分析(PCA)是一种受广泛应用的正交分解方法,它通过计算多维数据集中的潜在关联性,构建出新的坐标系,用于捕捉数据的关联规律。
它可以用来确定给定数据集中的重要特征,并将原始特征转化为更低维度的新特征,从而更好地捕捉数据本身的结构。
独立分量分析(ICA)也是正交分解的一种,它首先估计数据集中的线性独立特征,然后对原始特征进行线性变换,将其转化为更低维度的新特征,从而排除数据中的冗余特征。
它可以用来提取数据中存在的其他信息,比如数据中的异常值或复杂模式。
因子分析(FA)是一种正交分解的变化形式,它使用因子的概念来简化原始数据的表示,从而减少特征空间的维度,并有助于提取数据的有用特征。
它还可以用来分析和比较不同的数据集之间的关系,从而更好地理解这些数据的联系以及它们之间的关系。
正交分解可以为研究人员提供多方面的信息和洞察,它可以用来提取可用数据中的有用信息,有助于做出正确的决策和推导。
它在科学研究,商业运算,投资决策,机器学习和许多其他方面都有着巨大的发挥空间,因此它在许多领域中都被广泛应用。
综上所述,正交分解是研究多变量数据的一种有效的数学分析方法,它可以帮助研究人员挖掘数据中的有价值信息,从而更好地理解数据本身的结构,在许多领域得到了广泛的应用。