湍流预混火焰模型(1)

PDF 模型概率密度函数PDF方法以随机的观点来对待湍流问题，对解决湍流化学反应流的问题具有很强的优势。

在湍流燃烧中存在一些非输运量( 如反应速率, 密度, 温度及气相体积分数等) 的湍流封闭问题。

尽管这些量没有输运方程, 但它们常常是输运变量的已知函数。

平均或者过滤高度非线性的化学反应源项会引起方程的封闭问题。

因此，用PDF的方法来解决这些非输运量的湍流封闭问题显然是一个既简单又直接的途径。

PDF方法是一种较为流行的湍流燃烧模型，能够较为精确的模拟任何详细的化学动力学过程, 适用于预混、非预混和部分预混的任何燃烧问题。

目前, 确定输运变量脉动概率密度函数的方法有输运方程和简化假定两种, 分别称之为输运方程的PDF和简化的PDF。

前者建立输运变量脉动的概率密度输运方程，通过求解该方程来获得输运变量脉动的概率分布。

后者假定输运变量脉动的概率密度函数的具体形式, 通过确定其中的一些待定参数来获得输运变量脉动的概率分布。

湍流燃烧中, 后者应用最为普遍和广泛。

在简化的PDF 中, 输运变量脉动的概率密度函数常常采用双 D 分布、截尾高斯分布和B 函数分布等形式。

PDF在理论上可以精确考虑任意详细的化学反应机理，但是其具体求解时需借助其它的模型和算法，而且计算量相对较大。

PDF的方程是由N-S方程推导而来，其中的化学反应源项是封闭的，但压力脉动梯度项以及分子粘性和分子扩散引起的PDF的分子输运项是不封闭的，需要引入模型加以封闭。

例如，在速度- 标量-湍流频率PDF中，必须采用小尺度混合模型、随机速度模型和湍流频率模型加以封闭。

模化后的输运方程难以用有限容积、有限差分和有限元等方法来求解，比较可行的一种方法是蒙特卡洛(MonteCarlo)方法,在该方法中输运方程被转化为拉格朗日(Lagrangian)方程,流体由大量遵循Lagrang ian方程的随机粒子的系统来描述, 最后对粒子作统计平均得到流场物理量和各阶统计矩。

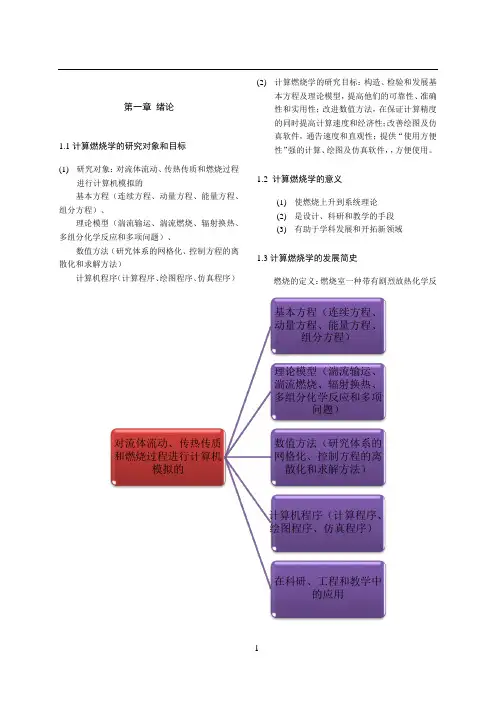
第一章绪论1.1计算燃烧学的研究对象和目标(1)研究对象：对流体流动、传热传质和燃烧过程进行计算机模拟的基本方程（连续方程、动量方程、能量方程、组分方程）、理论模型（湍流输运、湍流燃烧、辐射换热、多组分化学反应和多项问题）、数值方法（研究体系的网格化、控制方程的离散化和求解方法）计算机程序（计算程序、绘图程序、仿真程序）(2)计算燃烧学的研究目标：构造、检验和发展基本方程及理论模型，提高他们的可靠性、准确性和实用性；改进数值方法，在保证计算精度的同时提高计算速度和经济性；改善绘图及仿真软件，通告速度和直观性；提供“使用方便性”强的计算、绘图及仿真软件，，方便使用。

1.2 计算燃烧学的意义(1)使燃烧上升到系统理论(2)是设计、科研和教学的手段(3)有助于学科发展和开拓新领域1.3计算燃烧学的发展简史燃烧的定义：燃烧室一种带有剧烈放热化学反应的流动现象，它包含着流动、传热、传质和化学对流体流动、传热传质和燃烧过程进行计算机模拟的基本方程（连续方程、动量方程、能量方程、组分方程）理论模型（湍流输运、湍流燃烧、辐射换热、多组分化学反应和多项问题）数值方法（研究体系的网格化、控制方程的离散化和求解方法）计算机程序（计算程序、绘图程序、仿真程序）在科研、工程和教学中的应用反应以及它们之间的相互作用。

实际燃烧过程几乎都是湍流过程。

计算燃烧学特点：(1)兼顾研究理论模型和数值方法(2)及研究理论模型和数值方法，有中式计算机程序的编制和更新。

(3)既重视通用模型、通用方法和通用程序的研究，又重视与实际应用得密切结合。

1.4 内容梗概(1)构造基本方程和理论模型燃烧过程涉及的基本定律：物质不灭定律、牛顿第二定律、能量转换和守恒定律、组分转换和平衡定律等。

控制燃烧过程的基本方程组：连续方程、动量方程、能量方程、组分方程需要模化的分过程有：湍流输运、燃烧、辐射转换、多项流动和燃烧。

(2)数值方法数值方法主要包括：研究体系的网格化、控制方程的离散化、离散化方程的求解方法。

第33卷　第2期　1999年2月 西　安　交　通　大　学　学　报JO URNAL OF XI′AN JIAOTONG UN IVERSITY　Vol.33　№2 Feb.1999预混湍流火焰结构的分形特征蒋德明,马凡华,杨　迪(西安交通大学,710049,西安)摘要:使用分形几何学的方法,对由高速纹影摄影法获得的容弹内预混湍流火焰照片进行了处理.结果表明,容弹内预混湍流火焰结构具有分形特征,可以用分数维数来定量描述其折皱、扭曲程度及与湍流强度的关系.关键词:火焰结构;分形几何;燃烧学中国图书资料分类法分类号:TK411The Fractal Nature of Tu rbulent PremixedFlame StructureJiang Dem ing,Ma Fanhua,Yang Di(Xi′an Jiaotong University,Xi′an710049,C hina)A bstract:The fractal geometry method is used to analyze the hig h speed schlieren film of turbulentpremixed combustion for a co nstant volume combustion bom b.The fractal dimension can be used to describe the ex tent of w rinkling deg ree quantitatively and to exhibits a relation for the root mean square turbulent velocity.Keywords:flame structure;fractal geometry;combustion theory 大量研究表明,在实际火花点火发动机中的预混湍流燃烧均属于高度折皱的层流火焰[1].但长期以来,对高度折皱层流火焰的结构一直缺乏定量的描述和研究.1987年,F.C.Gouldin首先将分形的概念引入预流湍流燃烧研究之中[2].本文的目的是给出求取容弹内预混湍流火焰分数维数的具体方法,以及分数维数随u′/S L(u′和S L分别为湍流强度和层流燃烧速度)的变化规律,并导出相应的结论.1　从火焰照片求取分数维数的方法根据分形几何学理论,对各向均匀的分形,只需求出相应曲线的分数维数D2,即可用下式求得曲面的分数维数D3D3=D2+1(1)此外,有收稿日期:1998-03-02.作者简介:蒋德明,男,1934年4月生,能源与动力工程学院汽车工程系,教授,博士生导师. 基金项目:国家“八五”攀登计划资助项目(85-25-2-1).-D 2=lg N (ε)lg ε(2)1-D 2=lg L (ε)lg ε(3)1.1　直接法用不同的测量尺度ε沿曲线逐段测量,即可得到不同测量尺度时的总测量次数N (ε)以及曲线的总长度L (ε),L (ε)=ε·N (ε),然后,将测量结果以对数形式绘成坐标,即可得到其分数维数及内、外界.由于N (ε)或L (ε)是直接测得的(相对下面而言),故作者称之为“直接法”.1.2　面积法画一个半径为ε的圆,该圆中心位于曲线上;然后,沿曲线移动该圆(该圆的中心始终在曲线上),即形成宽度为2ε的“带子”,如图1所示;通过测量得到这一“带子”的面积A (ε)后,由A (ε)/2ε,即可求得相应的曲线长度(带长)L ;改变测量尺度ε,并重复上述过程,即可得到不同ε时的曲线长度L (ε),这样得到L (ε)与ε的对数坐标图,从而根据对数坐标图上的直线段,即可求得曲线的分数维数和相应的内、外界.由于曲线长度是通过测量“带子”的面积而得到的,故称之为“面积法”.图1　求取曲线分数维数的面积法示意图对火焰前锋外廓线,一般按上述方法用计算机进行处理.火焰前锋外廓线在计算机中是以离散的像素点来表示的,在运用面积法时,将所有到火焰外廓线(由一系列离散的像素点组成)的距离小于或等于ε的像素点累加起来,而每个像素点都对应于一定的面积,由此即可求得“带子”的面积,进而可求得其分数维数与内、外界.1.3　计算结果运用直接法和面积法,对本实验拍摄的火焰纹影胶片进行了计算处理,所得结果分别如图2和图3所示,图中坐标均为对数值.由图可知,这2个图中分别存在相应的直线段,其斜率所对应的分数维数D 2分别为1.095和1.101(相应地,其D 3值分别为2.095和2.101),这表明该湍流火焰具有分形特征,其分数维数D 2取为1.10.由图2可以看出,用直接法得不到明显的内、外界值εi 和εo ,而用面积法能够得到相应的εi 、εo 值.由图3可知,其外界εo 大约为8.3mm (100.92=8.3mm ),而内界εi 为1.7mm (100.24=1.7mm ).应该指出,由于图形空间分辨率的限制(大约在0.5mm 左右),由图2所得到的内界是不准确的.采用直接法求取分数维数时,在实际计算过程中只考虑了彼此连结的像素点的情况,因而所得到的曲线长度数值有较明显的波动,所以得不到明显的内、外界值;而采用面积法时,将所有不相连接的像素点都考虑进去,因而所得曲线长度值相当准确,且得到的分数维数比用直接法所得到的值略大一点,这与R .D .M atthew s 等人的结果是一致的[3].图2　用“直接法”处理火焰外廓线的结果图3　用“面积法”处理火焰外廓线的结果2　试验结果及分析图4为点火时刻在不同的湍流条件下,火焰半径R 大约为18m m 时容弹中的湍流火焰纹影照23第2期 蒋德明,等:预混湍流火焰结构的分形特征 (a )u ′i =0.2m /s ;L i =3.0mm (b )u ′i =0.8m /s ;L i =3.2mm (c )u ′i =1.5m /s ;L i =4.0mm 甲烷-空气; =0.9;　p i =101.3kPa ;　T i =300K图4　点火时刻不同湍流强度时的火焰纹影照片片.由图可以看出,点火时刻的湍流强度增大,则火焰前锋折皱程度加大,火焰结构也变得更为精细.图5为容弹内湍流火焰的分数维数D 3值随u ′/S L 的变化曲线.随着u ′/S L 的增大,在相同火 图5　容弹中湍流火焰的分数维数D 3值随u ′/S L 的变化曲线焰半径R 处,火焰前锋面的分数维数也增大.这表明其火焰前锋面的折皱、扭曲(粗糙)程度加大,从而增加了火焰前锋面的面积,因此燃烧反应在更大的火焰前锋面内进行,其瞬时质量燃烧率也随之增加,火焰燃烧速度加快.这一结果揭示出,在中、小程度的湍流强度条件下,湍流燃烧速度随湍流强度增大而增加的真正原因. 表1为4个实验工况下对应不同火焰半径处火焰前锋面的分数维数D 3值.由此可知,在同一实验工况下,当火焰半径增大时,其分数维数D 3是增加的.这表明,在容弹内预混湍流燃烧过程中,随着火焰半径增加,火焰前锋的折皱程度增加,因此其火焰燃烧速度也相应地增大.同时也进一步证实,本研究容弹内的预混湍流燃烧属非充分发展的湍流火焰,湍流对燃烧影响(促进作用)是一个渐进的过程,随着火焰的不断发展,这一促进作用愈加明显和强烈.表1　4个实验工况下的分数维数D 3值点火时刻的湍流参数u ′i =1.5m /s L i =4.0mmu ′i =0.8m /s L i =3.2mmu ′i =1.0m /s L i =3.5mmu ′i =0.7m /s L i =3.0mm当量燃空比0.90.90.70.7D 3(R =13mm )2.082.062.092.07D 3(R =25mm )2.122.092.132.093　结　论(1)火花点火发动机内的预混湍流火焰具有分形特征.(2)在中、小程度的湍流强度下,分数维数随湍流强度的增加而增加,湍流燃烧速度增大.(3)火花点火发动机中的预混湍流火焰属于非充分发展湍流火焰.参考文献:[1]　蒋德明.火花点火发动机的燃烧.西安:西安交通大学出版社,1992.[2]　Gouldin F C .A n application of fractals to modelling pre -mix ed turbulent flame .Combustion and F lame ,1987,68:249～266.[3]　Hall M J ,M atthew s R D .Fractal analysis of turbulentpremixed flame images from SI engines .SAE P aper 922242,1992.(编辑　蒋慧姝)24西　安　交　通　大　学　学　报 第33卷。

预混燃烧的燃烧模型摘要为了达到抑制污染物排放，实现燃料的清洁燃烧的目的，人们采取了很多办法。

“节能减排”促使燃烧系统采用贫燃燃烧技术，它具有降低NOx、CO等污染物，提高燃烧效率的作用。

但这种燃烧方式的燃烧极限范围很窄，而且火焰稳定性差，容易诱发燃烧系统的不稳定性，如火焰的热声耦合振荡，这种不稳定性会造成更大的污染和浪费。

新型燃烧器的设计必须克服这些缺点，以达到“节能减排”的目的。

首先本文以FLUENT软件为平台，构建了合理的数学物理模型，对甲烷-空气预混燃烧过程进行了数值模拟，实验证明，贫燃料燃烧及贫氧燃烧都可以起到降低污染物排放的目的。

并利用数值模拟的方法针对不同燃烧模型的情况下甲烷的预混燃烧的特性进行分析，观察其NO）的分布情况，发现预混燃烧的相关规律，寻求燃烧速度场、温度场、以及污染物（X的最佳工况。

其次本文了解不同燃烧模型对流场结构、燃烧结构的影响，与实验结果比较，探讨如何改进数值模拟，提高设计精度，同时找出预混火焰稳定性规律，探讨抑制燃烧不稳定性的策略。

本文通过数值计算，得到了在不同燃烧模型下柱状燃烧室内甲烷燃烧的数值模拟结果，分析发现，燃烧模型的不同对甲烷燃烧特性的影响也不同。

通过对燃烧速度分布图，火焰温度分布云图，燃烧的污染物NO的云图进行分析研究，得出结论。

关键词预混燃烧数值模拟FLUENT 部分预混燃烧Title Pre-mixing combustion combustion modelAbstractIn order to achieve inhibit pollutants, realize fuel clean burning purpose, people taken a lot of measures. "Energy conservation and emission reduction" prompted combustion system using poor fuel combustion technology, it has to reduce pollutants such as NOx, CO, increase the combustion efficiency role. But this kind of combustion way combustion limit range is very narrow, and flame stability is poor, and likely to cause combustion system instability, such as flame of thermoacoustic oscillation, the coupling instability will cause more pollution and waste. New burner's design must overcome these shortcomings, to achieve "the purpose of energy saving and emission reduction".Firstly this paper with FLUENT software for the platform, and constructs the reasonable mathematical physics model of methane - air pre-mixing combustion process was simulated, the experiment proof, the poor fuel combustion and poor oxygen burning can reducing pollutant purpose. And using the method of numerical simulation of combustion model for different under the condition of pre-mixing combustion characteristics of methane areanalyzed, observe its velocity field and temperature field, and the distribution of pollutants (), found the relevant law pre-mixing combustion, seeking the best condition burning. Then this paper to understand different combustion model convection field structure, the influence of combustion structure, compared with the experimental results, this paper discusses how to improve the design accuracy numerical simulation, and at the same time, improve the stability pre-mixed flame out rules and explore the inhibiting combustion instability strategy.This article through numerical calculation, obtained in different combustion model columnar combustion chamber under the numerical simulation results of methane combustion, analysis, we found that the different combustion model for the influence of methane combustion characteristic of different also. Through the burning rate distribution, the flame temperature distribution of convective, the combustion pollutants analysis of NO cloud, draws the conclusion.Keywords：Pre-mixing combustion Numerical simulation FLUENT Part pre-mixing combustion绪论课题的研究背景及意义燃烧室作为燃气轮机中最重要的部件，是利用燃料的燃烧，提高进入涡轮的气流温度的装置。