相似三角形练习题(解析)

浙教新版九年级上册《4.5相似三角形的性质及其应用》2024年同步练习卷（3）一、选择题：本题共4小题，每小题3分，共12分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如图所示的网格由边长相同的小正方形组成，点A，B，C，D，E，F，G均在小正方形的顶点上，则的重心是()A.点GB.点DC.点ED.点F2.如图，在中，E，G分别是AB，AC上的点，，的平分线AD交EG于点F，若，则()A.B.C.D.3.如图，的两条中线AD和BE相交于点G，过点E作交AD于点F，则FG：AG是()A.1：4B.1：3C.1：2D.2：34.如图，正方形ABCD中，E为CD的中点，，交BC于点F，则与的大小关系为()A.B.C.D.无法确定二、填空题：本题共6小题，每小题3分，共18分。

5.如图，在中，点D，E分别是BC，AC的中点，AD与BE相交于点若，则EF的长是______.6.如图，AD是的高，AE是的外接圆的直径，且，，，则的直径______.7.点G是的重心，，如果，那么AB的长是______.8.如图，E，F分别为AC，BC的中点，D是EC上一点，且若，，则BE的长为______.9.如图，在等腰中，，，点E在边CB上，，点D在边AB上，，垂足为F，则AD的长为______.10.如图，点D在的边BC上，已知点E、点F分别为和的重心，如果，那么两个三角形重心之间的距离EF的长等于______.三、解答题：本题共3小题，共24分。

解答应写出文字说明，证明过程或演算步骤。

11.本小题8分已知，如图，在中，CD是斜边上的中线，交BC于点F，交AC的延长线于点∽吗？为什么？你能推出结论吗？请试一试．12.本小题8分已知：如图，在中，点D、E分别在边BC、AB上，，AD与CE相交于点F，求证：；求证：13.本小题8分如图，在中，，，动点M从点B出发，在BA边上以每秒3cm的速度向定点A运动，同时动点N从点C出发，在CB边上以每秒2cm的速度向点B运动，运动时间为t秒，连接若与相似，求t的值；连接AN，CM，若，求t的值．答案和解析1.【答案】B【解析】解：取BC的中点N，取AC的中点M，连接AN，BM，如图所示，则AN与BM的交点为D，故点D是的重心，故选：取BC的中点N，取AC的中点M，连接AN，BM，然后根据图形可知AN与BM的交点为D，即可得到点D 为的重心．本题考查三角形的重心，解答本题的关键是明确三角形的重心是三角形中线的交点．2.【答案】C【解析】解：，，，，∽，故选：根据两组对应角相等可判断∽，可得，则可得出结论．本题考查了相似三角形的判定与性质，灵活运用定理是关键．3.【答案】A【解析】【分析】本题考查的是三角形的重心的概念和性质、平行线分线段成比例定理的应用，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍，根据重心的性质得到，，根据平行线分线段成比例定理计算即可．【解答】解：的两条中线AD和BE相交于点G，点G是的重心，，，，，：：4，故选：4.【答案】C【解析】解：，，，，∽，且相似比为2，，，又，∽，易证∽，求得CF的长，可得根据勾股定理即可求得AE、EF的长，即可判定∽，即可解题．本题考查了相似三角形的判定，相似三角形对应边比值相等的性质，相似三角形对应角相等的性质，本题中求证∽是解题的关键．5.【答案】3【解析】解：点D，E分别是BC，AC的中点，，且，，，，故答案为：由题意可知，DE是的中线，则，且，可得，代入BF的长，可求出EF的长，进而求出BE的长．本题主要考查三角形中位线，平行线分线段成比例等知识，熟练掌握相关知识是解题的关键．6.【答案】【解析】【分析】本题考查了圆周角定理，相似三角形的性质和判定的应用，解此题的关键是求出∽首先根据两个对应角相等可以证明三角形相似，再根据相似三角形的性质得出关于AE的比例式，计算即可．【解答】解：由圆周角定理可知，，，，∽：：AC，，，，：：5，，故答案为：7.【答案】6【解析】解：如图，AD为AB边上的中线，点G是的重心，，，，故答案为先根据三角形重心的性质得到，则，然后根据直角三角形斜边上的中线性质得到AB的长．本题考查了三角形的重心：重心到顶点的距离与重心到对边中点的距离之比为2：也考查了直角三角形斜边上的中线性质．8.【答案】【解析】解：，，，∽，，，，E，F分别为AC，BC的中点，，，解得：故答案为：由可得：，结合公共角，可证得∽，从而利用相似三角形的对应中线之比等于相似比即可求BE的长．本题主要考查相似三角形的判定与性质，解答的关键是明确相似三角形的对应中线的之等于相似比．9.【答案】【解析】解：过D作于H，在等腰中，，，，，，，，，，∽，，，，，，，故答案为：过D作于H，根据等腰三角形的性质得到，，求得，得到，根据相似三角形的性质即可得到结论．本题考查了相似三角形的判定和性质，等腰直角三角形的判定和性质，正确的作出辅助线是解题的关键．10.【答案】【解析】解：如图，连接AE并延长交BD于G，连接AF并延长交CD于H，点E、F分别是和的重心，，，，，，，，，，∽，，，故答案为：连接AE并延长交BD于G，连接AF并延长交CD于H，根据三角形的重心的概念、相似三角形的性质解答．本题考查了三角形重心的概念和性质，三角形的重心是三角形中线的交点，三角形的重心到顶点的距离等于到对边中点的距离的2倍．11.【答案】证明：，，，，，∽；为的中线，，，又，，又是公共角，∽，，即【解析】根据题意，得，，则，易证∽；由中，CD是斜边上的中线，得，则，又，所以，又是公共角，所以∽，即可得出；本题主要考查了直角三角形和相似三角形的判定与性质，掌握直角三角形斜边上的中线等于斜边的一半，是解答本题的关键．12.【答案】证明：，，，，，，∽，，；∽，，即，，，∽，，，，【解析】根据等腰三角形的性质得到，，推出∽，根据相似三角形的性质得到，于是得到；根据相似三角形的性质得到，即，推出∽，根据相似三角形的性质得到，于是得到，等量代换即可得到结论．本题考查了相似三角形的判定和性质，等腰三角形的性质，三角形的外角的性质，证得∽是解题的关键．13.【答案】解：，，，，由题意得，，当∽时，，即，解得：；当∽时，，即，解得：，综上所述，与相似时，t的值为或；如图，过点M作于点D，，，∽，，，，，，，，，，，，，，，∽，，即，解得：【解析】根据勾股定理求出AB，分∽、∽两种情况，根据相似三角形的性质列出比例式，计算即可；过点M作于点D，分别证明∽，∽，根据相似三角形的性质列出比例式，计算即可．本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键．。

几何推理练习题相似三角形几何推理练习题：相似三角形几何推理是数学中的一种重要思维方式，通过观察、分析和推理几何图形的属性来解决问题。

相似三角形是几何推理中常见的一种情况，它们具有相等的夹角，并且对应边的比例相等。

本文将介绍一些相似三角形的练习题，帮助读者巩固几何推理的能力。

1. 练习题一已知△ABC中，∠A=45°，∠B=60°，AB=5 cm。

连接点A和点D，使得∠BCD=90°。

如果AD=4 cm，求BC的长度。

解析：根据题目可以得知，△ABC和△BCD为相似三角形，因为∠A=∠BCD。

根据相似三角形的性质，可以列出比例关系式：AB/BC = BC/BD代入已知数值，可得：5/BC = BC/4通过交叉相乘求解，得到：BC^2 = 20因此，BC = √20 = 2√5 cm。

2. 练习题二已知△ABC和△ADE相似，且BC=8 cm，AC=10 cm，DE=12 cm。

如果BD=9 cm，求AE的长度。

解析：根据题目可以得知，△ABC和△ADE为相似三角形，因此可以列出比例关系式：AB/AE = BC/DE代入已知数值，可得：AB/AE = 8/12 = 2/3通过交叉相乘求解，得到：AB * 3 = AE * 2已知BD=9 cm，根据△ABD的相似比例关系，可以得到：AB/BD = AE/DE代入已知数值，可得：AB/9 = AE/12将AB的值代入上述等式，可得：(2/3) * 9 = AE/12通过简单的计算，可以得到：AE = 2 * 9 / 3 = 6 cm因此，AE的长度为6 cm。

3. 练习题三已知两个相似三角形，它们的周长比为7:4，面积比为49:16。

求这两个三角形的边长比和面积比。

解析：设两个相似三角形的边长比为a:b，面积比为c:d。

根据题目可得以下比例关系：(a+b)/(c+d) = 7/4 --（1）(a^2+b^2)/(c^2+d^2) = 49/16 --（2）将（1）式两边同乘4(c+d)，可得：4(a+b) = 7(c+d)化简后得：4a + 4b = 7c + 7d --（3）将（2）式两边同乘16(c^2+d^2)，可得：16(a^2+b^2) = 49(c^2+d^2)化简后得：16a^2 + 16b^2 = 49c^2 + 49d^2 --（4）由（3）式可得：4(a+b) - 7(c+d) = 0化简后得：4a + 4b - 7c - 7d = 0 --（5）由（4）式可得：16(a^2 + b^2) - 49(c^2 + d^2) = 0化简后得：16a^2 + 16b^2 - 49c^2 - 49d^2 = 0 --（6）通过求解方程组（5）和（6），可以得到a:b的值为7:4，c:d的值为49:16。

第四章 图形的相似4.5 相似三角形判定定理的证明精选练习一、单选题1．（2022·全国·九年级课时练习）ABC V 和A B C ¢¢¢V 符合下列条件，其中使ABC V 与A B C ¢¢¢V 不相似的是（ ）A ．45A A ¢Ð=Ð=°，26B Ð=°，109B ¢Ð=°B ．1AB =， 1.5AC =，2BC =，12A B ¢¢=，8A C ¢¢=，16B C ¢¢=C ．A B ¢Ð=Ð， 1.5AB =，1514AC =，32A B ¢¢=， 2.1B C ¢¢=D ．BC a =，AC b =，AB c =，B C ¢¢=A C ¢¢=A B ¢¢=【点睛】本题主要考查了相似三角形的判定，三角形内角和定理，解题的关键在于能够熟练掌握相似三角形的判定条件．V斜边上的高，则图中相似三角形的对数有（）2．（2022·全国·九年级课时练习）如图，CD是Rt ABCA．0对B．1对C．2对D．3对【答案】D【分析】直角三角形斜边上的高线分原三角形所得到的两个三角形与原三角形相似，由此即可解答.【详解】由题意得：△ADC∽△ACB；△ADC∽△CDB；△CDB∽△AC B．故选D．【点睛】本题解决的关键是熟知直角三角形斜边上的高线分原三角形所得到的了两个三角形与原三角形相似这一定理．3．（2022·全国·九年级课时练习）在△ABC和△A1B1C1中，下列四个命题（1）若AB=A1B2，AC=A1C1，∠A在∠A，则△ABC≌△A1B1C1；（2）若AB=A1B2，AC=A1C1，∠B=∠B1，则△ABC≌△A1B1C1；（3）若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1；（4）若AC：A1C1=CB：C1B1，∠C=∠C1，则△ABC∽△A1B1C1．其中真命题的个数为（）A．4个B．3个C．2个D．1个【答案】B【分析】分别利用相似三角形的判定和全等三角形的判定定理进行判断即可得到正确的选项．【详解】解：（1）若AB＝A1B1，AC＝A1C1，∠A＝∠A1，能用SAS定理判定△ABC≌△A1B1C1，故（1）正确；（2）若AB＝A1B1，AC＝A1C1，∠B＝∠B1，不能用ASS判定△ABC≌△A1B1C1，故（2）错误；（3）若∠A＝∠A1，∠C＝∠C1，能判定△ABC∽△A1B1C1，故（3）正确；（4）若AC：A1C1＝CB：C1B1，∠C＝∠C1，能利用两组对应边的比相等且夹角相等的两三角形相似判定△ABC∽△A1B1C1，故（4）正确．正确的个数有3个；故选：B ．【点睛】本题考查了命题与定理的知识，解题的关键是掌握三角形全等和相似的判定方法．4．（2021·黑龙江·肇源县第五中学八年级期中）如图，在ABC V 中，点P 在边AB 上，则在下列四个条件中：ACP B Ð=Ð①；APC ACB Ð=Ð②；2AC AP AB =×③；AB CP AP CB ×=×④，能满足APC V 与ACB V 相似的条件是（ ）A ．①②④B ．①③④C ．②③④D ．①②③【答案】D 【分析】根据相似三角形的判定定理，结合图中已知条件进行判断.【详解】当ACP B Ð=Ð，A A Ð=ÐQ ，所以APC V ∽ACB V ,故条件①能判定相似，符合题意；当APC ACB Ð=Ð，A A Ð=ÐQ ，所以APC V ∽ACB V ，故条件②能判定相似，符合题意；当2AC AP AB =×，即AC ：AB AP =：AC ，因为A AÐ=Ð所以APC V ∽ACB V ，故条件③能判定相似，符合题意；当AB CP AP CB ×=×，即PC ：BC AP =：AB ，而PAC CAB Ð=Ð，所以条件④不能判断APC V 和ACB V 相似，不符合题意；①②③能判定相似，故选：D ．【点睛】本题考查相似三角形的判定，熟练掌握判定定理是解题的关键.5．下列各组图形必相似的是（ ）A ．任意两个等腰三角形B ．两边为1和2的直角三角形与两边为2和4的直角三角形C ．有两边对应成比例，且有一个角对应相等的两三角形D ．两边及其中一边上的中线对应成比例的两三角形【答案】D【分析】根据相似三角形的判定定理可分别判断各选项是否足以证明三角形相似，从而判断选项的正确性.【详解】A. 任意两个等腰三角形，各内角的值不确定，故无法证明三角形相似，故本选项错误;B.因为不能判定已知边2和4是直角边还是斜边，故无法判定三角形相似，故本选项错误；C. 两边对应成比例，必须夹角相等才能判定三角形相似，故本选项错误;D. 两边和一边的中线均对应成比例，即可以判定两三角形中对应成比例的边的夹角相等，即可判定三角形相似，故本选项正确.故本题选D.【点睛】本题考查相似三角形的判定定理.熟练掌握相似三角形的判定定理，能根据相似三角形的判定定理判断是否满足判定条件是解决本题的关键.6．（2022·河北唐山·九年级期末）图中四个阴影的三角形中与△ABC 相似的是（ ）A ．B ．C ．D ．二、填空题7．（ΔABC 与△DEF 中，65A Ð=°，42B Ð=°，65D Ð=°，73F Ð=°，3AB =，5AC =，6BC =，6DE =，10DF =，12EF =，则△DEF 与△ABC ________【答案】相似【分析】根据相似三角形的判定方法解答即可.【详解】∵65A Ð=°，42B Ð=°，∴∠C =180°-65°-42°=73°.∵65D Ð=°，73F Ð=°，∴∠A =∠D, ∠C =∠F,∴△DEF 与△ABC 相似.故答案为相似.【点睛】本题考查了相似三角形的判定方法，相似三角形的判定方法有：①对应角相等，对应边成比例的两个三角形叫做相似三角形；②平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似；③两角相等的两个三角形相似；④两边对应成比例，且夹角相等的两个三角形相似判定即可；⑤三边对应成比例的两个三角形相似.8．（2021·全国·九年级专题练习）如图，已知，90ACB ADC Ð=Ð=o ，3BC =，4AC =，要使ABC ACD V V ∽，只要CD =________．9．如图所示，D ，E 分别在△ABC 的边AB 、AC 上，DE 与BC 不平行，当满足________条件时，有△ABC ∽△AE D ．10．（2022·全国·九年级课时练习）如图，8AB =，50A Ð=゜，''4A B =，''3A C =．当AC =________，'A Ð=________时，'''ABC A B C V V ∽．三、解答题11．（2022·全国·九年级课时练习）已知：如图，在△ABC 和△A ′B ′C ′中，∠A =∠A ′，∠B =∠B ′．求证：△ABC ∽△A ′B ′C ′．【答案】证明见解析【分析】在△ABC 的边AB 上截取AD =A ′B ′，过点D 作BC 的平行线，交AC 于点E ，可证△ADE ∽△ABC ；再证△ADE ≌△A ′B ′C ′即可．【详解】证明：在△ABC 的边AB 上截取AD =A ′B ′，过点D 作BC 的平行线，交AC 于点E ，则∠ADE =∠B ，△ADE ∽△AB C ．∵∠A =∠A ′，∠ADE =∠B =∠B ′，AD =A ′B ′，∴△ADE ≌△A ′B ′C ′，∴△ABC ∽△A ′B ′C ′【点睛】本题考查了相似三角形的判定定理的证明，解题关键是通过作辅助线，构建全等三角形进行证明．12．（2021·全国·九年级课时练习）已知：如图，在ABC V 和A B C ¢¢¢V 中，,AB AC A A A B A C Ð=Т=¢¢¢¢．求证：ABC A B C ¢¢¢∽△△．一、填空题1．（2018·上海第二工业大学附属龚路中学九年级阶段练习）ABC D 中，10AB =，6AC =，点D 在AC 上，且3AD =，若要在AB 上找一个点E ，使ADE D 与ABC D 相似，则AE =__．2．已知△ABC 和△DEF 中．点A 、B 、C 分别与点D 、E 、F 相对应．且∠A ＝70°时，∠B ＝34°，∠D ＝70°，则当∠F ＝_____时，△ABC ∽△DEF ．【答案】76°【分析】利用两对角相等的三角形相似即可作出判断．【详解】∵△ABC 和△DEF 中．点A 、B 、C 分别与点D 、E 、F 相对应．且∠A =70°时，∠B =34°，∠D =70°，∴∠B =∠E =34°，∴∠C =∠F =76°，故答案为76°【点睛】此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．3．（2022·山东烟台·八年级期末）如图，在ABCD Y 中，点E 在AB 上，CE BD ，交于点F ，若:4:3AE BE =，且2BF =，则DF =_________．4．如图，在△AB C中，点P在AB上，下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件有______________.【答案】①②③【分析】根据有两组角对应相等的两个三角形相似可对①②进行判断；根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断．【详解】①、当∠ACP=∠B，∵∠A=∠A，∴△APC∽△ACB，∴①符合题意；②、当∠APC=∠ACB，∵∠A=∠A，∴△APC∽△ACB，∴②符合题意；③、当AC2=AP•AB，即AC：AB=AP：AC，∵∠A=∠A∴△APC∽△ACB，∴③符合题意；④、∵当AB•CP=AP•CB，即PC：BC=AP：AB，而∠PAC=∠CAB，∴不能判断△APC和△ACB相似，∴④不符合题意；故答案为①②③．【点睛】本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．5．如图所示，在△AB C中，AB＝8cm，BC＝16 cm.点P从点A出发沿AB向点B以2 cm/s的速度运动，点Q从点B出发沿BC向点C以4 cm/s的速度运动．如果点P，Q分别从点A，B同时出发，则_____________秒钟后△PBQ与△ABC相似？情况讨论，避免漏解而导致出错．二、解答题6．（2022·全国·九年级课时练习）如图，123Ð=Ð=Ð，求证：ABC D 与ADE D 相似.【答案】证明见解析【分析】两个三角形的若是有两组角相等，那么这两个三角形是相似三角形．根据题意可分别求出两组角相等，从而知道△ABC 与△ADE 相似．【详解】∵∠1=∠2，∴∠1+∠DAC =∠2+∠DAC ，即∠BAC =∠DAE ，又∵在△AHE 和△DH C 中，∠2=∠3，∠AHE =∠DHC∴∠C =∠E ，在△ABC 和△ADE 中∵∠E =∠C ，∠BAC =∠DAE ，∴△ABC ∽△ADE ．【点睛】本题考查相似三角形的判定定理，两个三角形的两组角对应相等，那么这两个个三角形互为相似三角形．7．（2022·甘肃酒泉·九年级期末）如图，在△AB C 中，AB ＝8cm ，BC ＝16cm ，点P 从点A 开始沿边AB 向点B 以2cm/s 的速度移动，点Q 从点B 开始沿边BC 向点C 以4cm/s 的速度移动，如果点P 、Q 分别从点A 、B 同时出发，经几秒钟△PBQ 与△ABC 相似？试说明理由．8．如图已知，在△AB C中，CD⊥AB，BE⊥AC，BE交CD于点O，求证：△ABE∽△OCE.【答案】证明见解析.【分析】要证明△ABE∽△OCE，需先找对证明两三角形相似的条件，根据已知条件找出即可证明.【详解】Q CD⊥AB，BE⊥AC，\∠AEB＝∠ADC＝90°.又∠A＝∠A，\∠ABE＝∠OCE.又Q∠AEB＝∠OEC，\△ABE∽△OCE.【点睛】此题重点考察学生对证明两三角形相似的理解，熟练两三角形相似的证明方法是解题的关键.。

实用标准文案相似三角形一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= _________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t 的值；若不存在，请说明理由．9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD 、AC 把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q 作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ 为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB 上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC 交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P 为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．解答：证明：∵DE∥BC，∴DE∥FC，∴∠AED=∠C．又∵EF∥AB，∴EF∥AD，∴∠A=∠FEC．∴△ADE∽△EFC．点评：本题考查的是平行线的性质及相似三角形的判定定理．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．解答：（1）证明：∵梯形ABCD，AB∥CD，∴∠CDF=∠FGB，∠DCF=∠GBF，（2分）∴△CDF∽△BGF．（3分）（2）解：由（1）△CDF∽△BGF，又F是BC的中点，BF=FC，∴△CDF≌△BGF，∴DF=GF，CD=BG，（6分）∵AB∥DC∥EF，F为BC中点，∴E为AD中点，∴EF是△DAG的中位线，∴2EF=AG=AB+BG．∴BG=2EF﹣AB=2×4﹣6=2，∴CD=BG=2cm．（8分）3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．解答：证明：∵FD∥AB，FE∥AC，∴∠B=∠FDE，∠C=∠FED，∴△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．解答：证明：∵矩形ABCD中，AB∥CD，∠D=90°，（2分）∴∠BAF=∠AED．（4分）∵BF⊥AE，∴∠AFB=90°．∴∠AFB=∠D．（5分）∴△ABF∽△EAD．（6分）点评：考查相似三角形的判定定理，关键是找准对应的角．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．解答：（1）证明：①∵∠BAC=∠DAE，∴∠BAE=∠CAD，∵AB=AC，AD=AE，∴△ABE≌△ACD，∴BE=CD．②由△ABE≌△ACD，得∠ABE=∠ACD，BE=CD，∵M、N分别是BE，CD的中点，∴BM=CN．又∵AB=AC，∴△ABM≌△ACN．∴AM=AN，即△AMN为等腰三角形．（2）解：（1）中的两个结论仍然成立．（3）证明：在图②中正确画出线段PD，由（1）同理可证△ABM≌△ACN，∴∠CAN=∠BAM∴∠BAC=∠MAN．又∵∠BAC=∠DAE，∴∠MAN=∠DAE=∠BAC．∴△AMN，△ADE和△ABC都是顶角相等的等腰三角形．∴△PBD和△AMN都为顶角相等的等腰三角形，∴∠PBD=∠AMN，∠PDB=∠ANM，∴△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．分析：根据平行线的性质和两角对应相等的两个三角形相似这一判定定理可证明图中相似三角形有：△AEF∽△BEC；△AEF∽△DCF；△BEC∽△DCF．解答：解：相似三角形有△AEF∽△BEC；△AEF∽△DCF；△BEC∽△DCF．（3分）如：△AEF∽△BEC．在▱ABCD中，AD∥BC，∴∠1=∠B，∠2=∠3．（6分）∴△AEF∽△BEC．（7分）7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= 135°°，BC= ；（2）判断△ABC与△DEC是否相似，并证明你的结论．解答：解：（1）∠ABC=135°，BC=；（2）相似；∵BC=，EC==；∴，；∴；又∠ABC=∠CED=135°，∴△ABC∽△DEC．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA 方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t 的值；若不存在，请说明理由解：（1）设经过x秒后，△AMN的面积等于矩形ABCD面积的，则有：（6﹣2x）x=×3×6，即x2﹣3x+2=0，（2分）解方程，得x1=1，x2=2，（3分）经检验，可知x1=1，x2=2符合题意，所以经过1秒或2秒后，△AMN的面积等于矩形ABCD面积的．（4分）（2）假设经过t秒时，以A，M，N为顶点的三角形与△ACD相似，由矩形ABCD，可得∠CDA=∠MAN=90°，因此有或（5分）即①，或②（6分）解①，得t=；解②，得t=（7分）经检验，t=或t=都符合题意，所以动点M，N同时出发后，经过秒或秒时，以A，M，N为顶点的三角形与△ACD相似．（8分）9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．解答：解：（1）任选两个三角形的所有可能情况如下六种情况：①②，①③，①④，②③，②④，③④（2分）其中有两组（①③，②④）是相似的．∴选取到的二个三角形是相似三角形的概率是P=（4分）证明：（2）选择①、③证明．在△AOB与△COD中，∵AB∥CD，∴∠CDB=∠DBA，∠DCA=∠CAB，∴△AOB∽△COD（8分）选择②、④证明．∵四边形ABCD是等腰梯形，∴∠DAB=∠CBA，∴在△DAB与△CBA中有AD=BC，∠DAB=∠CAB，AB=AB，∴△DAB≌△CBA，（6分）∴∠ADO=∠BCO．又∠DOA=∠COB，∴△DOA∽△COB（8分）．点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=，即相似三角形的证明．还考查了相似三角形的判定．10．附加题：如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．解答：解：（1）AD=DE，AE=CE．∵CE⊥BD，∠BDC=60°，∴在Rt△CED中，∠ECD=30°．∴CD=2ED．∵CD=2DA，∴AD=DE，∴∠DAE=∠DEA=30°=∠ECD．∴AE=CE．（2）图中有三角形相似，△ADE∽△AEC；∵∠CAE=∠CAE，∠ADE=∠AEC，∴△ADE∽△AEC；（3）作AF⊥BD的延长线于F，设AD=DE=x，在Rt△CED中，可得CE=，故AE=．∠ECD=30°．在Rt△AEF中，AE=，∠AED=∠DAE=30°，∴sin∠AEF=，∴AF=AE•sin∠AEF=．∴．点评：本题主要考查了直角三角形的性质，相似三角形的判定及三角形面积的求法等，范围较广．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．解答：解：（1）∵AB∥MP，QM∥AC，∴四边形APMQ 是平行四边形，∠B=∠PMC，∠C=∠QMB．∵AB=AC，∴∠B=∠C，∴∠PMC=∠QMB．∴BQ=QM，PM=PC．∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．（2）∵PM∥AB，∴△PCM∽△ACB，∵QM∥AC，∴△BMQ∽△BCA；（3）当点M中BC的中点时，四边形APMQ是菱形，∵点M是BC的中点，AB∥MP，QM∥AC，∴QM，PM是三角形ABC的中位线．∵AB=AC，∴QM=PM=AB=AC．又由（1）知四边形APMQ是平行四边形，∴平行四边形APMQ是菱形．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．解答：证明：∵正方形ABCD，M为CD中点，∴CM=MD=AD．∵BP=3PC，∴PC=BC=AD=CM．∴．∵∠PCM=∠ADM=90°，∴△MCP∽△ADM．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q 作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ 为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．解答：解：（1）过D作DH∥AB交BC于H点，∵AD∥BH，DH∥AB，∴四边形ABHD是平行四边形．∴DH=AB=8；BH=AD=2．∴CH=8﹣2=6．∵CD=10，∴DH2+CH2=CD2∴∠DHC=90°．∠B=∠DHC=90°．∴梯形ABCD是直角梯形．∴S ABCD=（AD+BC）AB=×（2+8）×8=40．（2）①∵BP=CQ=t ，∴AP=8﹣t，DQ=10﹣t，∵AP+AD+DQ=PB+BC+CQ，∴8﹣t+2+10﹣t=t+8+t．∴t=3＜8．∴当t=3秒时，PQ将梯形ABCD周长平分．②第一种情况：0＜t≤8若△PAD∽△QEC则∠ADP=∠C ∴tan∠ADP=tan∠C==∴=，∴t=若△PAD∽△CEQ则∠APD=∠C ∴tan∠APD=tan∠C==，∴=∴t=第二种情况：8＜t≤10，P、A、D三点不能组成三角形；第三种情况：10＜t≤12△ADP为钝角三角形与Rt△CQE不相似；∴t=或t=时，△PAD与△CQE相似．③第一种情况：当0≤t≤8时．过Q点作QE⊥BC，QH⊥AB，垂足为E、H．∵AP=8﹣t，AD=2，∴PD==．∵CE=t，QE=t，∴QH=BE=8﹣t，BH=QE=t．∴PH=t﹣t=t．∴PQ==，DQ=10﹣t．Ⅰ：DQ=DP，10﹣t=，解得t=8秒．Ⅱ：DQ=PQ，10﹣t=，化简得：3t2﹣52t+180=0解得：t=，t=＞8（不合题意舍去）∴t=第二种情况：8≤t≤10时．DP=DQ=10﹣t．∴当8≤t＜10时，以DQ为腰的等腰△DPQ恒成立．第三种情况：10＜t≤12时．DP=DQ=t﹣10．∴当10＜t≤12时，以DQ为腰的等腰△DPQ恒成立．综上所述，t=或8≤t＜10或10＜t≤12时，以DQ为腰的等腰△DPQ成立．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC 相似？解答：解：设经x秒后，△PBQ∽△BCD，由于∠PBQ=∠BCD=90°，（1）当∠1=∠2时，有：，即；（2）当∠1=∠3时，有：，即，∴经过秒或2秒，△PBQ∽△BCD．15．如图，在△ABC 中，AB=10cm ，BC=20cm ，点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动，如果P 、Q 分别从A 、B 同时出发，问经过几秒钟，△PBQ 与△ABC 相似． 解答： 设经过秒后t 秒后，△PBQ 与△ABC 相似，则有AP=2t ，BQ=4t ，BP=10﹣2t ， 当△PBQ ∽△ABC 时，有BP ：AB=BQ ：BC ， 即（10﹣2t ）：10=4t ：20，解得t=2.5（s ）（6分）当△QBP ∽△ABC 时，有BQ ：AB=BP ：BC ， 即4t ：10=（10﹣2t ）：20，解得t=1．所以，经过2.5s 或1s 时，△PBQ 与△ABC 相似（10分）．解法二：设ts 后，△PBQ 与△ABC 相似，则有，AP=2t ，BQ=4t ，BP=10﹣2t分两种情况：（1）当BP 与AB 对应时，有=，即=，解得t=2.5s （2）当BP 与BC 对应时，有=，即=，解得t=1s所以经过1s 或2.5s 时，以P 、B 、Q 三点为顶点的三角形与△ABC 相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB 的长为多少时，这两个直角三角形相似． 解答： 解：∵AC=，AD=2，∴CD==．要使这两个直角三角形相似，有两种情况：1） 当Rt △ABC ∽Rt △ACD 时， 2） 有=，∴AB==3；3） 当Rt △ACB ∽Rt △CDA 时， 4） 有=，∴AB==3．故当AB 的长为3或3时，这两个直角三角形相似．17．已知，如图，在边长为a 的正方形ABCD 中，M 是AD 的中点，能否在边AB 上找一点N （不含A 、B ），使得△CDM 与△MAN 相似？若能，请给出证明，若不能，请说明理由．解答： 证明：分两种情况讨论：①若△CDM ∽△MAN ，则=．∵边长为a ，M 是AD 的中点， ∴AN=a ．②若△CDM ∽△NAM ，则．∵边长为a，M 是AD的中点，∴AN=a，即N点与B重合，不合题意．所以，能在边AB上找一点N（不含A、B），使得△CDM与△MAN相似．当AN=a时，N点的位置满足条件．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？解答：解：设经过x秒后，两三角形相似，则CQ=（8﹣2x）cm，CP=xcm，（1分）∵∠C=∠C=90°，∴当或时，两三角形相似．（3分）（1）当时，，∴x=；（4分）（2）当时，，∴x=．（5分）所以，经过秒或秒后，两三角形相似．（6分）点评：本题综合考查了路程问题，相似三角形的性质及一元一次方程的解法．19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．解答：解：（1）若点A，P，D分别与点B，C，P对应，即△APD∽△BCP，∴=，∴=，∴AP2﹣7AP+6=0，∴AP=1或AP=6，检测：当AP=1时，由BC=3，AD=2，BP=6，∴=，又∵∠A=∠B=90°，∴△APD∽△BCP．当AP=6时，由BC=3，AD=2，BP=1，又∵∠A=∠B=90°，∴△APD∽△BCP．（2）若点A，P，D分别与点B，P，C对应，即△APD∽△BPC．∴=，∴=，∴AP=．检验：当AP=时，由BP=，AD=2，BC=3，∴=，又∵∠A=∠B=90°，∴△APD∽△BPC．因此，点P的位置有三处，即在线段AB距离点A的1、、6处．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC 交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．解答：证明：（1）∵△ABC是等腰直角三角形，∴∠MBE=45°，∴∠BME+∠MEB=135°又∵△DEF是等腰直角三角形，∴∠DEF=45°∴∠NEC+∠MEB=135°∴∠BEM=∠NEC，（4分）而∠MBE=∠ECN=45°，∴△BEM∽△CNE．（6分）（2）与（1）同理△BEM∽△CNE，∴．（8分）又∵BE=EC，∴，（10分）则△ECN与△MEN中有，又∠ECN=∠MEN=45°，∴△ECN∽△MEN．（12分）21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P 为顶点的三角形与△ABC相似．解答：解：以点Q、A、P为顶点的三角形与△ABC相似，所以△ABC∽△PAQ或△ABC∽△QAP，①当△ABC∽△PAQ 时，，所以，解得：t=6；②当△ABC∽△QAP时，，所以，解得：t=；③当△AQP∽△BAC时，=，即=，所以t=；④当△AQP∽△BCA时，=，即=，所以t=30（舍去）．故当t=6或t=时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？解答：解：∵∠MAC=∠MOP=90°，∠AMC=∠OMP，∴△MAC∽△MOP．∴，即，解得，MA=5米；同理，由△NBD∽△NOP，可求得NB=1.5米，∴小明的身影变短了5﹣1.5=3.5米．23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．解答：解：（1）皮尺，标杆；（2）测量示意图如图所示；（3）如图，测得标杆DE=a，树和标杆的影长分别为AC=b，EF=c，∵△DEF∽△BAC，∴，∴，∴．（7分）24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）解答：解：（1）由题意可知：∠BAC=∠EDF=90°，∠BCA=∠EFD．∴△ABC ∽△DEF．∴，即，（2分）∴DE=1200（cm）．所以，学校旗杆的高度是12m．（3分）（2）解法一：与①类似得：，即，∴GN=208．（4分）在Rt△NGH中，根据勾股定理得：NH2=1562+2082=2602，∴NH=260．（5分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（6分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN，∴（7分），又ON=OK+KN=OK+（GN﹣GK）=r+8，∴，解得：r=12．∴景灯灯罩的半径是12cm．（8分）解法二：与①类似得：，即，∴GN=208．（4分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（5分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN．∴，即，（6分）∴MN=r，又∵ON=OK+KN=OK+（GN﹣GK）=r+8．（7分）在Rt△OMN中，根据勾股定理得：r2+（r）2=（r+8）2即r2﹣9r﹣36=0，解得：r1=12，r2=﹣3（不合题意，舍去），∴景灯灯罩的半径是12cm．（8分）25．（2007•白银）阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．解答：解：∵AE∥BD，∴△ECA∽△DCB，∴．∵EC=8.7m，ED=2.7m，∴CD=6m．∵AB=1.8m，∴AC=BC+1.8m，∴，∴BC=4，即窗口底边离地面的高为4m．点评：此题基本上难度不大，利用相似比即可求出窗口底边离地面的高．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．解答：解：（1）由已知：AB∥OP，∴△ABC∽△OPC．∵，∵OP=l，AB=h，OA=a，∴，∴解得：．（2）∵AB∥OP，∴△ABC∽△OPC，∴，即，即．∴．同理可得：，∴=是定值．（3）根据题意设李华由A到A'，身高为A'B'，A'C'代表其影长（如图）．由（1）可知，即，∴，同理可得：，∴，由等比性质得：，当李华从A走到A'的时候，他的影子也从C移到C'，因此速度与路程成正比∴，所以人影顶端在地面上移动的速度为．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．解：设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c，则c2=a2+b2（1）S1=S2+S3；（2）S1=S2+S3．证明如下：显然，S1=，S2=，S3=∴S2+S3==S1；（3）当所作的三个三角形相似时，S1=S2+S3．证明如下：∵所作三个三角形相似∴∴=1 ∴S1=S2+S3；（4）分别以直角三角形ABC三边为一边向外作相似图形，其面积分别用S1、S2、S3表示，则S1=S2+S3．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．解答：解：∵△ABC ∽△ADE，∴AE：AC=AD：AB．∵AE：AC=（AB+BD）：AB，∴AE：9=（15+5）：15．∴AE=12．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．解答：解：（1）Rt△ABC中，根据勾股定理得：BC==5，∵Rt△ABC∽Rt△BDC，∴==，==，∴BD=，CD=；（2）在Rt△BDC中，S△BDC=BE•CD=BD•BC，∴BE===3．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．解：（1）设=k，那么x=2k，y=3k，z=5k，由于3x+4z﹣2y=40，∴6k+20k﹣6k=40，∴k=2，∴x=4，y=6，z=10．（2）设一个三角形周长为Ccm，则另一个三角形周长为（C+560）cm，则，∴C=240，C+560=800，即它们的周长分别为240cm，800cm。

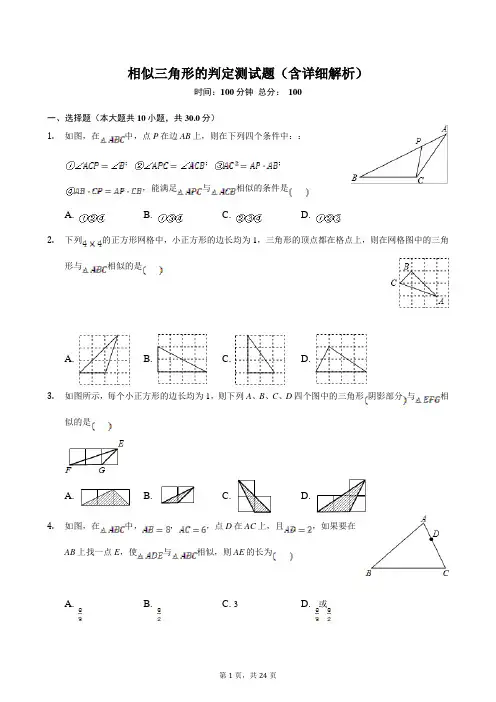
相似三角形的判定测试题（含详细解析）时间：100分钟总分：100一、选择题（本大题共10小题，共30.0分）1.如图，在中，点P在边AB上，则在下列四个条件中：：；；；，能满足与相似的条件是A. B. C. D.2.下列的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则在网格图中的三角形与相似的是A. B. C. D.3.如图所示，每个小正方形的边长均为1，则下列A、B、C、D四个图中的三角形阴影部分与相似的是A. B. C. D.4.如图，在中，，，点D在AC上，且，如果要在AB上找一点E，使与相似，则AE的长为A. B. C. 3 D. 或5.如图，在正方形ABCD中，点E，F分别在BC，CD上，且，将绕点A顺时针旋转，使点E落在点处，则下列判断不正确的是A. 是等腰直角三角形B. AF垂直平分C. ∽D. 是等腰三角形6.如图，在中，点D，E分别在边AB，AC上，下列条件中不能判断∽的是A.B.C.D.7.如图，点D，E分别在的AB，AC边上，增加下列条件中的一个：，，，，，使与一定相似的有A. B. C. D.8.如图，在钝角三角形ABC中，，，动点D从A点出发到B点止，动点E从C点出发到A点止点D运动的速度为秒，点E运动的速度为秒如果两点同时运动，那么当以点A、D、E为顶点的三角形与相似时，运动的时间是A. 4或B. 3或C. 2或4D. 1或69.如图，在中，，，，将沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是A. B.C. D.10.如图，点E是矩形ABCD的边AD的中点，且于点F，则下列结论中错误的是A.B.C. 图中与相似的三角形共有4个D.二、填空题（本大题共10小题，共30.0分）11.如图，已知中，D为边AC上一点，P为边AB上一点，，，，当AP的长度为______ 时，和相似．12.如图，在中，、E分别为边AB、AC上的点，，点F为BC边上一点，添加一个条件：______，可以使得与相似只需写出一个13.在中，，，点D在边AB上，且，点E在边AC上，当______时，以A、D、E为顶点的三角形与相似．14.如图，，，，，，点p在BD上移动，当______时，和相似．15.如图，中，D、E分别是AB、AC边上一点，连接请你添加一个条件，使∽，则你添加的这一个条件可以是______写出一个即可．16.如图所示，中，E，F分别是边AB，AC上的点，且满足，则与的面积比是______ ．17.已知在中，，，E是边AB上一点，且，若F是AC边上的点，且以A、E、F为顶点的三角形与相似，则AF的长为______．18.如图，在中，，，，点M在AB边上，且，过点M作直线MN与AC边交于点N，使截得的三角形与原三角形相似，则______ ．19.如图，在正方形网格上有6个三角形：，，，，，．在中，与相似的三角形的个数是______．三、计算题（本大题共4小题，共24.0分）20.如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．求证：≌；求证：∽．21.如图，在中，D、E分别是AB、AC上的点，，，AD：：3，的角平分线AF交DE于点G，交BC于点F．请你直接写出图中所有的相似三角形；求AG与GF的比．22.如图，已知，，垂足分别为B、D，AD与BC相交于点E，，垂足为F，试回答图中，∽______ ，∽______ ，∽______ ．23.在图中，的内部任取一点O，连接AO、BO、CO，并在AO、BO、CO这三条线段的延长线上分别取点D、E、F，使，画出你认为与相似吗？为什么？你认为它们也具有位似形的特征吗？四、解答题（本大题共2小题，共16.0分）24.如图所示，，，，点P从点B出发，沿BC向点C以的速度移动，点Q从点C出发沿CA向点A以的速度移动，如果P、Q分别从B、C同时出发，过多少时，以C、P、Q为顶点的三角形恰与相似？25.如图，四边形ABCD中，AC平分，，，E为AB的中点．求证：∽；与AD有怎样的位置关系？试说明理由；若，，求的值．答案和解析【答案】1. D2. B3. B4. D5. D6. A7. A8. B9. C10. C11. 4或912. ，或13. 或14. 或12cm或2cm15.16.17. 1：918. 或19. 4或620. 321. 证明：正方形ABCD，等腰直角三角形EDF，，，，，，在和中，，≌；延长BA到M，交ED于点M，≌，，即，，，，，，∽．22. 解：∽，∽，∽；，，，又，∽，，为角平分线，∽，，．23. DAB；BCD；DCE24. 解：相似如图，，，∽，，同理，∽，它们也具有位似形的特征．25. 解：设经过y秒后，∽，此时，．，，，．∽，，设经过y秒后，∽，此时，．．∽，所以，经过秒或者经过后两个三角形都相似26. 解：平分，，又，：：AB，∽；，理由：∽，，又为AB的中点，，，，，；，，，，，，∽，，．【解析】1. 解：当，，所以∽；当，，所以∽；当，即AC：：AC，所以∽；当，即PC：：AB，而，所以不能判断和相似．故选D．根据有两组角对应相等的两个三角形相似可对进行判断；根据两组对应边的比相等且夹角对应相等的两个三角形相似可对进行判断．本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．2. 解：根据勾股定理，，，所以，夹直角的两边的比为，观各选项，只有B选项三角形符合，与所给图形的三角形相似．故选：B．可利用正方形的边把对应的线段表示出来，利用三边对应成比例两个三角形相似，分别计算各边的长度即可解题．此题考查了勾股定理在直角三角形中的运用，三角形对应边比值相等判定三角形相似的方法，本题中根据勾股定理计算三角形的三边长是解题的关键．3. 解：小正方形的边长为1，在中，，，，A中，一边，一边，一边，三边与中的三边不能对应成比例，故两三角形不相似故A错误；B中，一边，一边，一边，有，即三边与中的三边对应成比例，故两三角形相似故B正确；C中，一边，一边，一边，三边与中的三边不能对应成比例，故两三角形不相似故C 错误；D中，一边，一边，一边，三边与中的三边不能对应成比例，故两三角形不相似故D错误．故选：B．根据相似三角形的判定，易得出的三边的边长，故只需分别求出各选项中三角形的边长，分析两三角形对应边是否成比例即可．本题考查了相似三角形的判定识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角，可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法．4. 解：是公共角，当，即时，∽，解得：；当，即时，∽，解得：，的长为：或．故选D．由是公共角，分别从当，即时，∽与当，即时，∽，去分析求解即可求得答案．此题考查了相似三角形的判定注意分类讨论思想的应用．5. 解：将绕点A顺时针旋转，使点E落在点处，，，是等腰直角三角形，故A正确；将绕点A顺时针旋转，使点E落在点处，，四边形ABCD是正方形，，，，，，，垂直平分，故B正确；，，，，∽，故C正确；，但不一定等于，不一定是等腰三角形，故D错误；故选D．由旋转的性质得到，，于是得到是等腰直角三角形，故A正确；由旋转的性质得到，由正方形的性质得到，推出，于是得到AF垂直平分，故B正确；根据余角的性质得到，于是得到∽，故C 正确；由于，但不一定等于，于是得到不一定是等腰三角形，故D错误．本题考查了旋转的性质，正方形的性质，相似三角形的判定，等腰直角三角形的判定，线段垂直平分线的判定，正确的识别图形是解题的关键．6. 解：，当或时，∽；当即时，∽．故选：A．根据相似三角形的判定定理进行判定即可．本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．7. 解：，，∽，正确；，，∽，正确；，，∽，正确；由，或不能证明与相似．故选：A．由两角相等的两个三角形相似得出正确，由两边成比例且夹角相等的两个三角形相似得出正确；即可得出结果．本题考查了相似三角形的判定定理：两角对应相等的两个三角形相似；两边对应成比例且夹角相等的两个三角形相似；三边对应成比例的两个三角形相似；如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．8. 解：根据题意得：设当以点A、D、E为顶点的三角形与相似时，运动的时间是x秒，若∽，则AD：：AC，即x：：12，解得：；若∽，则AD：：AB，即x：：6，解得：；所以当以点A、D、E为顶点的三角形与相似时，运动的时间是3秒或秒．故选B．根据相似三角形的性质，由题意可知有两种相似形式，∽和∽，可求运动的时间是3秒或秒．此题考查了相似三角形的性质，解题时要注意此题有两种相似形式，别漏解；还要注意运用方程思想解题．9. 解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确．D、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误；故选：C．根据相似三角形的判定定理对各选项进行逐一判定即可．本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．10. 解：A、，∽，，，，故A正确，不符合题意；B、过D作交AC于N，，，四边形BMDE是平行四边形，，，，于点F，，，，，故B正确，不符合题意；C、图中与相似的三角形有，，，，共有5个，故C错误．D、设，由∽，有．，故D正确，不符合题意．故选C．由，又，所以，故A正确，不符合题意；过D作交AC于N，得到四边形BMDE是平行四边形，求出，得到，根据线段的垂直平分线的性质可得结论，故B正确，不符合题意；根据相似三角形的判定即可求解，故C正确，不符合题意；由∽，得到CD与AD的大小关系，根据正切函数可求的值，故D错误，符合题意．本题考查了相似三角形的判定和性质，矩形的性质，图形面积的计算，正确的作出辅助线是解题的关键．11. 解：当∽时，，，解得：，当∽时，，，解得：，当AP的长度为4或9时，和相似．故答案为：4或9．分别根据当∽时，当∽时，求出AP的长即可．此题主要考查了相似三角形的判定与性质，利用倒推法以及分类讨论得出是解题关键．12. 解：，或．理由：，，∽，当时，∽，∽．当时，，∽．故答案为，或．结论：，或根据相似三角形的判定方法一一证明即可．本题考查相似三角形的判定和性质平行线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．13. 解：当时，，∽，此时；当时，，∽，此时；故答案为：或．若A，D，E为顶点的三角形与相似时，则或，分情况进行讨论后即可求出AE的长度．本题考查了相似三角形的判定，熟练掌握相似三角形的判定方法，解题的关键是分两种情况进行讨论．14. 解：由，，，设，则，若∽，则，即，变形得：，即，因式分解得：，解得：，，所以或12cm时，∽；若∽，则，即，解得：，，综上，或12cm或时，∽．故答案为：或12cm或2cm．设出，由表示出PD的长，若∽，根据相似三角形的对银边成比例可得比例式，把各边的长代入即可列出关于x的方程，求出方程的解即可得到x的值，即为PB的长．此题考查了相似三角形的判定与性质，相似三角形的性质有相似三角形的对应边成比例，对应角相等；相似三角形的判定方法有：1、两对对应角相等的两三角形相似；2、两对对应边成比例且夹角相等的两三角形相似；3、三边对应成比例的两三角形相似，本题属于条件开放型探究题，其解法：类似于分析法，假设结论成立，逐步探索其成立的条件．15. 解：当时，∽．故答案为．利用平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似进行添加条件．本题考查了相似三角形的判定：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似．16. 解：，当时，∽．故答案为．利用有两组角对应相等的两个三角形相似添加条件．本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．17. 解：，，又，∽，与的面积比：9，故答案为：1：9．由已知条件易证∽，根据相似三角形的性质即可求出与的面积比．本题考查了相似三角形的判定和性质，熟悉相似三角形的性质：相似三角形的面积比是相似比的平方是解题关键．18. 解：，以A、E、F为顶点的三角形与相似，有∽和∽两种情况：如图1：当时，∽时，即，解得：；如图2：当时，∽时，即，解得：．所以或．故答案为或．根据相似三角形的相似比求AF，注意分情况考虑．本题考查了相似三角形的判定，熟练掌握相似三角形的判定定理，分情况讨论是解决本题的关键．19. 解：如图1，当时，则∽，故，则，解得：，如图2所示：当时，又，∽，，即，解得：，故答案为：4或6．分别利用当时以及当时，得出相似三角形，再利用相似三角形的性质得出答案．此题主要考查了相似三角形判定，正确利用分类讨论得出是解题关键．20. 解：，，，，，，，，，，，，，，，与不相似；，，，∽；，，，∽；，，，，，，与不相似．故答案为3．先利用勾股定理计算出，，，，，，然后利用三组对应边的比相等的两个三角形相似依次判断，，，，与是否相似．本题考查了相似三角形的判定：三组对应边的比相等的两个三角形相似也考查了勾股定理．21. 由正方形ABCD与等腰直角三角形DEF，得到两对边相等，一对直角相等，利用SAS即可得证；由第一问的全等三角形的对应角相等，根据等量代换得到，再由对顶角相等，利用两对角相等的三角形相似即可得证．此题考查了全等三角形的判定与性质，以及相似三角形的判定与性质，熟练掌握各自的判定与性质是解本题的关键．22. 可得到三组三角形相似；先利用两组对应边的比相等且夹角对应相等的两个三角形相似证明∽，则，再利用有两组角对应相等的两个三角形相似证明∽，然后利用相似比和比例的性质求的值．本题考查了相似三角形的判断：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．23. 解：，，，，，，，，∽；，，，，∽，故答案为：DAB；BCD；DCE．由AB垂直于BD，CD垂直于BD，得到一对同旁内角互补，利用同旁内角互补两直线平行得到AB与CD 平行，同理EF与AB平行，且与CD平行，根据EF与AB平行，利用两直线平行同位角相等得到两对角相等，确定出三角形DEF与三角形DAB相似；同理得到三角形BEF与三角形BCD相似；由两直线平行得到两对内错角相等，得到三角形ABE与三角形DEC相似．此题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解本题的关键．24. 由，可得∽，再由相似得出对应边成比例，即可得出与相似，由于它们有位似中心点O，所以它们也具有位似形的特征．本题主要考查了相似三角形的判定以及位似图形的问题，应熟练掌握位似与相似之间的联系及区别．25. 设经过y秒后相似，由于没有说明对应角的关系，所以共有两种情况：∽与∽本题考查相似三角形的判定，解题的关键是分两种情况进行讨论，本题属于中等题型．26. 根据两组对应边的比相等且夹角对应相等的两个三角形相似进行求解；根据，，即可得出，进而得到；先根据，，判定∽，即可得出，进而得到．本题主要考查了相似三角形的判定与性质的运用，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合．。

相似三角形练习题一、填空题：1、若b m m a 2,3==，则_____:=b a 。

2、已知653zy x ==，且623+=z y ，则__________,==y x 。

3、在Rt △ABC 中，斜边长为c ，斜边上的中线长为m ，则______:=c m 。

4、反向延长线段AB 至C ，使AC ＝21AB ，那么BC ：AB ＝ 。

5、如果△ABC ∽△A ′B ′C ′，相似比为3：2，若它们的周长的差为40厘米，则 △A ′B ′C ′的周长为 厘米。

6、如图，△AED ∽△ABC ，其中∠1＝∠B ，则()()()AB BC AD_________==。

第6题图 第7题图7、如图，△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，若∠A ＝30°，则BD ：BC ＝ 。

若BC ＝6，AB ＝10，则BD ＝ ，CD ＝ 。

8、如图，梯形ABCD 中，DC ∥AB ，DC ＝2cm ，AB ＝3.5cm ，且MN ∥PQ ∥AB ， DM ＝MP ＝PA ，则MN ＝ ，PQ ＝ 。

第8题图 第9题图9、如图，四边形ADEF 为菱形，且AB ＝14厘米，BC ＝12厘米，AC ＝10厘米，那BE ＝ 厘米。

10、梯形的上底长1.2厘米，下底长1.8厘米，高1厘米，延长两腰后与下底所成的三角形的高为 厘米。

二、选择题：EAD B C 1C BD AD CM P N Q A B11、下面四组线段中，不能成比例的是（ ） A 、4,2,6,3====d c b a B 、3,6,2,1====d c b a C 、10,5,6,4====d c b a D 、32,15,5,2====d c b a12、等边三角形的中线与中位线长的比值是（ ）A 、1:3B 、2:3C 、23:21 D 、1：3 13、已知754zy x ==，则下列等式成立的是（ ） A 、91=+-y x y x B 、167=++z z y x C 、38=-+++z y x z y x D 、x z y 3=+14、已知直角三角形三边分别为b a b a a 2,,++，()0,0>>b a ，则=b a :（ ） A 、1：3 B 、1：4 C 、2：1 D 、3：115、△ABC 中，AB ＝12，BC ＝18，CA ＝24，另一个和它相似的三角形最长的一边是36，则最短的一边是（ ）A 、27B 、12C 、18D 、2016、已知c b a ,,是△ABC 的三条边，对应高分别为c b a h h h ,,，且6:5:4::=c b a ，那么c b a h h h ::等于（ ）A 、4：5：6B 、6：5：4C 、15：12：10D 、10：12：15 17、一个三角形三边长之比为4：5：6，三边中点连线组成的三角形的周长为30cm ，则原三角形最大边长为（ ）A 、44厘米B 、40厘米C 、36厘米D 、24厘米 18、下列判断正确的是（ ）A 、不全等的三角形一定不是相似三角形B 、不相似的三角形一定不是全等三角形C 、相似三角形一定不是全等三角形D 、全等三角形不一定是相似三角形19、如图，△ABC 中，AB ＝AC ，AD 是高，EF ∥BC ，则图中与△ADC 相似的三角形共有（ ）A 、1个B 、2个C 、3个D 、多于3个第19题图 第20题图A E F GB DC20、如图，在平行四边形ABCD 中，E 为BC 边上的点，若BE ：EC ＝4：5，AE 交BD 于F ，则BF ：FD 等于（ ）A 、4：5B 、3：5C 、4：9D 、3：8 三、解答题：21、已知()3:2:=-y y x ，求yx yx 2352-+的值。

相似三角形性质与判定专项练习30题(有答案)1.在三角形ABC中，点D在边BC上，且∠BAC=∠DAG，∠XXX∠BAD。

证明：=。

当GC⊥BC时，证明：∠BAC=90°。

2.在三角形ABC中，∠ACB=90°，点D在边BC上，CE⊥AB，CF⊥AD，E、F分别是垂足。

证明：AC^2=AF•AD。

联结EF，证明：AE•DB=AD•EF。

3.在三角形ABC中，PC平分∠ACB，PB=PC。

证明：△APC∽△ACB。

若AP=2，PC=6，求AC的长。

4.在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠XXX∠C。

证明：△ABF∽△EAD。

若AB=4，∠BAE=30°，求AE的长。

5.在三角形ABC中，∠ABC=2∠C，BD平分∠ABC。

证明：AB•BC=AC•CD。

6.在直角三角形ABC中，AC=BC，点E、F在AB上，∠ECF=45°，设△ABC的面积为S。

说明AF•BE=2S的理由。

7.在等边三角形ABC中，边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P。

若AE=CF，证明：AF=BE，并求∠APB的度数。

若AE=2，试求AP•AF的值。

若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长。

8.在钝角三角形ABC中，AD，BE是边BC上的高。

证明。

9.在三角形ABC中，AB=AC，DE∥BC，点F在边AC 上，DF与BE相交于点G，且∠XXX∠ABE。

证明：（1）△DEF∽△BDE；（2）DG•DF=DB•EF。

10.在等边三角形ABC、△DEF中，点D为AB的中点，E在BC上运动，DF和EF分别交AC于G、H两点，BC=2.问E在何处时CH的长度最大？11.在AB和CD交于点O的图形中，当∠A=∠C时，证明：OA•OB=OC•OD。

12.在等边三角形△AEC中，以AC为对角线做正方形ABCD（点B在△AEC内，点D在△AEC外）。

初三数学相似三角形典例及练习题含答案典例典例1已知三角形ABC中，∠B=90°，AC=6cm，BD垂直AC于D点，BD=3cm，求BC的长度。

解析：根据勾股定理可得：BC^2 = AB^2 + AC^2 = BD^2 + AD^2 + AC^2因为∆ABC与∆ABD相似，所以可以得到：\frac{AD}{AB}=\frac{AB}{AC}即：AD = \frac{AB^2}{AC}将公式代入原式中，得到：BC^2 = BD^2 + \frac{AB^4}{AC^2} + AC^2因为AC=6，BD=3，所以代入可得：BC^2 = 3^2 + \frac{AB^4}{6^2} + 6^2化简得：BC^2 = AB^4 \cdot \frac{1}{36} + 45AB^4 = 36(BC^2 - 45)因此，我们可以得到：AB = \sqrt[4]{36(BC^2 - 45)}典例2已知两个三角形ABC和DEF，且它们相似，已知AC=20cm，EF=12cm，AB=15cm，计算DE的长度。

解析：由于两个三角形相似，所以可以得到：\frac{AB}{DE}=\frac{AC}{EF}将已知条件带入即可得到：\frac{15}{DE}=\frac{20}{12}解得：DE = \frac{36}{4} = 9因此，DE的长度为9cm。

典例3已知三角形ABC和DEF相似，且AB=5cm，DE=2.5cm，BC=6cm，计算EF的长度。

解析：由于两个三角形相似，所以可以得到：\frac{AB}{DE}=\frac{BC}{EF}将已知条件带入即可得到：\frac{5}{2.5}=\frac{6}{EF}解得：EF = 12因此，EF的长度为12cm。

练习题练习题1已知三角形ABC中，∠B=90°，AB=3cm，AC=4cm，D、E、F分别是BC、AC、AB上的点，且∆DEF与∆ABC相似。

相似三角形(压轴必刷30题专项训练)一．填空题(共9小题)1(2020秋•虹口区校级月考)一张等腰三角形纸片，底边长为15cm ，底边上的高长22.5cm ．现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是第6张．【分析】设第x 张为正方形，如图，△ADE ∽△ABC ，则DE BC =AM AN，从而计算出x 的值即可．【解答】解：如图，设第x 张为正方形，则DE =3(cm )，AM =(22.5-3x )(cm )，∵△ADE ∽△ABC ，∴DE BC =AM AN ，即315=22.5-3x 22.5，解得x =6．故答案为：6．【点评】本题考查了相似三角形的判定和性质，等腰三角形的性质以及正方形的性质，注：相似三角形的对应边之比等于对应边上的高之比．2(2019秋•浦东新区校级月考)如图，在平行四边形ABCD 中，E 是边BC 上的点，AE 交BD 于点F ，如果BE BC=23，那么BF FD =23．【分析】由平行四边形的性质可证△BEF ∽△DAF ，再根据相似三角形的性质得BE ：DA =BF ：DF 即可解．【解答】解：ABCD 是平行四边形，∴BC ∥AD ，BC =AD∴△BEF ∽△DAF∴BE ：DA =BF ：DF∵BC =AD∴BF ：DF =BE ：BC =2：3．【点评】本题考查了平行四边形的性质及相似三角形的判定定理和性质．3(2017秋•虹口区校级月考)如图，直角三角形ABC 中，∠ACB =90°，AB =10，BC =6，在线段AB上取一点D ，作DF ⊥AB 交AC 于点F ，现将△ADF 沿DF 折叠，使点A 落在线段DB 上，对应点记为A 1；AD 的中点E 的对应点记为E 1，若△E 1FA 1∽△E 1BF ，则AD =165．【分析】利用勾股定理列式求出AC ，设AD =2x ，得到AE =DE =DE 1=A 1E 1=x ，然后求出BE 1，再利用相似三角形对应边成比例列式求出DF ，然后利用勾股定理列式求出E 1F ，然后根据相似三角形对应边成比例列式求解得到x 的值，从而可得AD 的值．【解答】解：∵∠ACB =90°，AB =10，BC =6，∴AC =AB 2-BC 2=102-62=8，设AD =2x ，∵点E 为AD 的中点，将△ADF 沿DF 折叠，点A 对应点记为A 1，点E 的对应点为E 1，∴AE =DE =DE 1=A 1E 1=x ，∵DF ⊥AB ，∠ACB =90°，∠A =∠A ，∴△ABC ∽△AFD ，∴AD AC =DF BC ，即2x 8=DF 6，解得DF =32x ，在Rt △DE 1F 中，E 1F =DF 2+DE 12=3x 22+x 2=13x 2，又∵BE 1=AB -AE 1=10-3x ，△E 1FA 1∽△E 1BF ，∴E 1F A 1E 1=BE 1E 1F ，∴E 1F 2=A 1E 1•BE 1，即(13x 2)2=x (10-3x )，解得x =85，∴AD 的长为2×85=165．故答案为：165．【点评】本题考查了相似三角形的性质，主要利用了翻折变换的性质，勾股定理，相似三角形对应边成比例，综合题，熟记性质并准确识图是解题的关键．4(2021秋•普陀区校级月考)如图，在△ABC 中，4AB =5AC ，AD 为△ABC 的角平分线，点E 在BC 的延长线上，EF ⊥AD 于点F ，点G 在AF 上，FG =FD ，连接EG 交AC 于点H ．若点H 是AC 的中点，则AG FD的值为43．【分析】解题关键是作出辅助线，如解答图所示：第1步：利用角平分线的性质，得到BD =54CD ；第2步：延长AC ，构造一对全等三角形△ABD ≌△AMD ；第3步：过点M 作MN ∥AD ，构造平行四边形DMNG ．由MD =BD =KD =54CD ，得到等腰△DMK ；然后利用角之间关系证明DM ∥GN ，从而推出四边形DMNG 为平行四边形；第4步：由MN ∥AD ，列出比例式，求出AG FD的值．【解答】解：已知AD 为角平分线，则点D 到AB 、AC 的距离相等，设为h ．∵BD CD =S △ABD S △ACD =12AB ⋅h 12AC ⋅h =AB AC =54，∴BD =54CD ．如图，延长AC ，在AC 的延长线上截取AM =AB ，则有AC =4CM ．连接DM ．在△ABD 与△AMD 中，AB =AM ∠BAD =∠MAD AD =AD ∴△ABD ≌△AMD (SAS )，∴MD =BD =54CD ．过点M 作MN ∥AD ，交EG 于点N ，交DE 于点K ．∵MN ∥AD ，∴CK CD =CM AC =14，∴CK =14CD ，∴KD =54CD ．∴MD =KD ，即△DMK 为等腰三角形，∴∠DMK =∠DKM ．由题意，易知△EDG 为等腰三角形，且∠1=∠2；∵MN ∥AD ，∴∠3=∠4=∠1=∠2，又∵∠DKM =∠3(对顶角)∴∠DMK =∠1，∴DM ∥GN ，∴四边形DMNG 为平行四边形，∴MN =DG =2FD ．∵点H 为AC 中点，AC =4CM ，∴AH MH=23．∵MN ∥AD ，∴AG MN =AH MH ，即AG 2FD =23，∴AG FD =43．故答案为：43．方法二：如图，有已知易证△DFE ≌△GFE ，故∠5=∠B +∠1=∠4=∠2+∠3，又∠1=∠2，所以∠3=∠B ，则可证△AGH ∽△ADB设AB =5a ，则AC =4a ，AH =2a ，所以AG /AD =AH /AB =2/5，而AD =AG +GD ，故GD /AD =3/5，所以AG ：GD =2：3，F 是GD 的中点，所以AG ：FD =4：3．【点评】本题是几何综合题，难度较大，正确作出辅助线是解题关键．在解题过程中，需要综合利用各种几何知识，例如相似、全等、平行四边形、等腰三角形、角平分线性质等，对考生能力要求较高．5(2022秋•普陀区校级月考)如图，点A 1，A 2，A 3，A 4在射线OA 上，点B 1，B 2，B 3在射线OB 上，且A 1B 1∥A 2B 2∥A 3B 3，A 2B 1∥A 3B 2∥A 4B 3．若△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，则图中三个阴影三角形面积之和为10.5．【分析】已知△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，且两三角形相似，因此可得出A 2B 2：A 3B 3=1：2，由于△A 2B 2A 3与△B 2A 3B 3是等高不等底的三角形，所以面积之比即为底边之比，因此这两个三角形的面积比为1：2，根据△A 3B 2B 3的面积为4，可求出△A 2B 2A 3的面积，同理可求出△A 3B 3A 4和△A 1B 1A 2的面积．即可求出阴影部分的面积．【解答】解：△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，又∵A 2B 2∥A 3B 3，A 2B 1∥A 3B 2，∴∠OB 2A 2=∠OB 3A 3，∠A 2B 1B 2=∠A 3B 2B 3，∴△B 1B 2A 2∽△B 2B 3A 3，∴B 1B 2B 2B 3=12=A 2B 2A 3B 3，∴A 2A 3A 3A 4=12．∵S △A 2B 2A 3S △B 2A 3B3=12，△A 3B 2B 3的面积是4，∴△A 2B 2A 3的面积为=12×S △A 2B 2B 3=12×4=2(等高的三角形的面积的比等于底边的比)．同理可得：△A 3B 3A 4的面积=2×S △A 3B 2B 3=2×4=8；△A 1B 1A 2的面积=12S △A 2B 1B 2=12×1=0.5．∴三个阴影面积之和=0.5+2+8=10.5．故答案为：10.5．【点评】本题的关键是利用平行线证明三角形相似，再根据已给的面积，求出相似比，从而求阴影部分的面积．6(2017秋•徐汇区校级月考)设△ABC 的面积为1，如图①，将边BC 、AC 分别2等分，BE 1、AD 1相交于点O ，△AOB 的面积记为S 1；如图②将边BC 、AC 分别3等分，BE 1、AD 1相交于点O ，△AOB 的面积记为S 2；⋯，依此类推，则S n 可表示为　12n +1　．(用含n 的代数式表示，其中n 为正整数)【分析】连接D 1E 1，设AD 1、BE 1交于点M ，先求出S △ABE 1=1n +1，再根据AB D 1E 1=BM ME 1=n +1n 得出S △ABM ：S △ABE 1=(n +1)：(2n +1)，最后根据S △ABM ：1n +1=(n +1)：(2n +1)，即可求出S n ．【解答】解：如图，连接D 1E 1，设AD 1、BE 1交于点M ，∵AE1：AC =1：(n +1)，∴S △ABE 1：S △ABC =1：(n +1)，∴S △ABE 1=1n +1，∵AB D 1E 1=BM ME 1=n +1n ，∴BM BE 1=n +12n +1，∴S △ABM ：S △ABE 1=(n +1)：(2n +1)，∴S △ABM ：1n +1=(n +1)：(2n +1)，∴S n =12n +1．故答案为：12n +1．【点评】此题考查了相似三角形的判定与性质，用到的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的面积，关键是根据题意作出辅助线，得出相似三角形．7(2018秋•南岗区校级月考)已知菱形ABCD 的边长是6，点E 在直线AD 上，DE =3，连接BE 与对角线AC 相交于点M ，则MC AM的值是　2或23　．【分析】由菱形的性质易证两三角形相似，但是由于点E 的位置未定，需分类讨论．【解答】解：分两种情况：(1)点E 在线段AD 上时，△AEM ∽△CBM ，∴MC AM =BC AE=2；(2)点E在线段AD的延长线上时，△AME∽△CMB，∴MCAM =BCAE=23．【点评】本题考查了相似三角形的性质以及分类讨论的数学思想；其中由相似三角形的性质得出比例式是解题关键．注意：求相似比不仅要认准对应边，还需注意两个三角形的先后次序．8(2020秋•虹口区校级月考)如图，在△ABC中，∠ACB的内、外角平分线分别交BA及其延长线于点D、E，BC=2.5AC，则ABAD+ABAE=5．【分析】根据CD平分∠ACB，可得ABDA=BCAC，根据CE平分∠ACB的外角，可得DEAE=BCAC，进而可得结果．【解答】解：∵CD平分∠ACB，∴AB DA =BC AC，∴BD+DADA =BC+ACAC，∴AB DA =BC+ACAC，①∵CE平分∠ACB的外角，∴DE AE =BC AC，∴BE-AEAE =BC-ACAC，∴AB AE =BC-ACAC，②①+②得，AB AD +ABAE=BC+ACAC+BC-ACAC=2BCAC=2×2.5=5．故答案为：5．【点评】主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用相似三角形的性质来分析、判断、推理或解答．9(2022秋•黄浦区校级月考)如图，在等腰△ABC中，AB=AC，点P在BA的延长线上，PA=1 4AB，点D在BC边上，PD=PC，则CDBC的值是　34　．【分析】过点P 作PE ∥AC 交DC 延长线于点E ，根据等腰三角形判定与性质，平行线的性质可证PB =PE ，再证△PCE ≌△PDB ，可得BD =CE ，再利用平行线分线段成比例的PA AB=CE BC ，结合线段的等量关系以及比例的性质即可得出结论．【解答】解：如图，过点P 作PE ∥AC 交DC 延长线于点E ，∵AB =AC ，∴∠B =∠ACB ，∵AC ∥PE ，∴∠ACB =∠E ，∴∠B =∠E ，∴PB =PE ，∵PC =PD ，∴∠PDC =∠PCD ，∴∠BPD =∠EPC ，∴在△PCE 和△PDB 中，PC =PD ∠BPD =∠EPC PB =PE，∴△PCE ≌△PDB (SAS )，∴BD =CE ，∵AC ∥PE ，∴PA AB =CE BC ，∵PA =14AB ，∴CE BC =14，∴BD BC =14，∴CD BC =34．故答案为：34．【点评】本题考查了等腰三角形的判定与性质，平行线分线段成比例，以及全等三角形的判定，解决问题的关键是正确作出辅助线，列出比例式．二．解答题(共21小题)10(2017秋•虹口区校级月考)在△ABC 中，∠CAB =90°，AD ⊥BC 于点D ，点E 为AB 的中点，EC 与AD交于点G ，点F 在BC 上．(1)如图1，AC ：AB =1：2，EF ⊥CB ，求证：EF =CD ．(2)如图2，AC ：AB =1：，EF ⊥CE ，求EF ：EG 的值．【分析】(1)根据同角的余角相等得出∠CAD =∠B ，根据AC ：AB =1：2及点E 为AB 的中点，得出AC =BE ，再利用AAS 证明△ACD ≌△BEF ，即可得出EF =CD ；(2)作EH ⊥AD 于H ，EQ ⊥BC 于Q ，先证明四边形EQDH 是矩形，得出∠QEH =90°，则∠FEQ =∠GEH ，再由两角对应相等的两三角形相似证明△EFQ ∽△EGH ，得出EF ：EG =EQ ：EH ，然后在△BEQ 中，根据正弦函数的定义得出EQ =12BE ，在△AEH 中，根据余弦函数的定义得出EH =32AE ，又BE =AE ，进而求出EF ：EG 的值．【解答】(1)证明：如图1，在△ABC 中，∵∠CAB =90°，AD ⊥BC 于点D ，∴∠CAD =∠B =90°-∠ACB ．∵AC ：AB =1：2，∴AB =2AC ，∵点E 为AB 的中点，∴AB =2BE ，∴AC =BE ．在△ACD 与△BEF 中，∠CAD =∠B ∠ADC =∠BFE =90°AC =BE，∴△ACD ≌△BEF ，∴CD =EF ，即EF =CD ；(2)解：如图2，作EH ⊥AD 于H ，EQ ⊥BC 于Q ，∵EH ⊥AD ，EQ ⊥BC ，AD ⊥BC ，∴四边形EQDH 是矩形，∴∠QEH =90°，∴∠FEQ =∠GEH =90°-∠QEG ，又∵∠EQF =∠EHG =90°，∴△EFQ ∽△EGH ，∴EF ：EG =EQ ：EH ．∵AC ：AB =1：3，∠CAB =90°，∴∠B =30°．在△BEQ 中，∵∠BQE =90°，∴sin B =EQ BE =12，∴EQ =12BE ．在△AEH中，∵∠AHE=90°，∠AEH=∠B=30°，∴cos∠AEH=EHAE =32，∴EH=32AE．∵点E为AB的中点，∴BE=AE，∴EF：EG=EQ：EH=12BE：32AE=1：3=3：3=33．【点评】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质，解直角三角形，综合性较强，有一定难度．解题的关键是作辅助线，构造相似三角形，并且证明四边形EQDH是矩形．11(2021秋•杨浦区校级月考)如图，已知在菱形ABCD，点E是AB的中点，AF⊥BC于点F，连接EF、ED、DF，DE交AF于点G，且DE⊥EF．(1)求证：AE2=EG•ED；(2)求证：BC2=2DF•BF．【分析】(1)根据直角三角形的性质得到AE=FE，根据菱形的性质得到AD∥BC，求得∠DAG=∠AFB =90°，然后证明△AEG∽△DEA，即可得到结论；(2)由AE=EF，AE2=EG•ED，得到FE2=EG•ED，推出△FEG∽△DEF，根据相似三角形的性质得到∠EFG=∠EDF，根据相似三角形的判定和性质即可得到结论．【解答】证明：(1)∵AF⊥BC于点F，∴∠AFB=90°，∵点E是AB的中点，∴AE=FE，∴∠EAF=∠AFE，∵四边形ABCD是菱形，∴AD∥BC，∴∠DAG=∠AFB=90°，∵DE⊥EF，∴∠FEG=90°，∴∠DAG=∠FEG，∵∠AGD=∠FGE，∴∠EFG=∠ADG，∴∠EAG=∠ADG，∵∠AEG=∠DEA，∴△AEG∽△DEA，∴AE DE =EG AE，∴AE2=EG•ED；(2)∵AE=EF，AE2=EG•ED，∴FE2=EG•ED，∴EF DE =EGEF，∵∠FEG=∠DEF，∴△FEG∽△DEF，∴∠EFG=∠EDF，∴∠BAF=∠EDF，∵∠DEF=∠AFB=90°，∴△ABF∽△DFE，∴AB DF =BF EF，∵四边形ACBD是菱形，∴AB=BC，∵∠AFB=90°，∵点E是AB的中点，∴FE=12AB=12BC，∴BC DF =BF12BC，∴BC2=2DF•BF．【点评】本题考查了相似三角形的判定和性质，菱形的性质，直角三角形的性质，正确的识别图形是解题的关键．12(2021秋•杨浦区校级月考)如图，已知在平行四边形ABCD中，AE：ED=1：2，点F为DC的中点，连接BE、AF，BE与AF交于点H．(1)求EH：BH的值；(2)若△AEH的面积为1，求平行四边形ABCD的面积．【分析】(1)延长AF，BC交于点G，证明△ADF≌△GCF(AAS)，可得AD=CG=BC，所以BG=2BC，根据AE：ED=1：2，可得AE：AD=1：3，AE：BG=1：6，，证明△AEH∽△GBH，即可解决问题；(2)在△AEH中，设AE=x，AE边上的高为h，△BGH中，BG边上的高为h′，可得平行四边形ABCD的高为h+h′，BC=3x，根据△AEH的面积为1，可得x•h=2，所以h′=6h，进而可以求平行四边形ABCD 的面积．【解答】解：(1)如图，延长AF，BC交于点G，∵四边形ABCD是平行四边形，∴AD ∥BC ，AD =BC ，∴∠D =∠DCG ，∠DAF =∠G ，∵点F 为DC 的中点，∴DF =CF ，在△ADF 和△GCF 中，∠D =∠FCG ∠DAF =∠G DF =CF，∴△ADF ≌△GCF (AAS )，∴AD =CG ，∴AD =CG =BC ，∴BG =2BC ，∵AE ：ED =1：2，∴AE ：AD =1：3，∴AE ：BG =1：6，∵AD ∥BC ，∴△AEH ∽△GBH ，∴EH ：BH =AE ：BG =1：6；(2)在△AEH 中，设AE =x ，AE 边上的高为h ，△BGH 中，BG 边上的高为h ′，∴平行四边形ABCD 的高为h +h ′，BC =3x ，∵△AEH 的面积为1，∴12x •h =1，∴x •h =2∵△AEH ∽△GBH ，∴h ：h ′=1：6，∴h ′=6h ，∴h +h ′=7h ，∴平行四边形ABCD 的面积=BC •(h +h ′)=3x •7h =21xh =42．【点评】本题考查了相似三角形的判定和性质，平行四边形的性质，平行线分线段成比例等知识，添加恰当辅助线构造相似三角形是解题的关键．13(2021春•徐汇区校级月考)如图，在菱形ABCD 中，点E 在对角线AC 上，点F 在BC 的延长线上，EF =EB ，EF 与CD 相交于点G ；(1)求证：EG •GF=CG •GD ；(2)联结DF ，如果EF ⊥CD ，那么∠FDC 与∠ADC 之间有怎样的数量关系？证明你的结论．【分析】(1)先证明△BCE ≌△DCE ，得∠EDC =∠EBC ；利用此条件再证明∠DGE ∽△FGC ，即可得到EG •GF =CG •GD．(2)利用第(1)题的结论，可证明△DGE ∽△FGC ，再利用三角形内角外角关系，即可得到∠ADC 与∠FDC 的关系．【解答】解：(1)证明：∵点E 在菱形ABCD 的对角线AC 上，∴∠ECB =∠ECD ，∵BC =CD ，CE =CE ，∴△BCE ≌△DCE ，∴∠EDC =∠EBC ，∵EB =EF ，∴∠EBC =∠EFC ；∴∠EDC =∠EFC ；∵∠DGE =∠FGC ，∴△DGE ∽△FGC ；∴EGCG =GD FG∴EG •GF =CG •GD ；(2)∠ADC =2∠FDC ．证明：∵EG CG =GD FG ，∴EG DG =CG FG，又∵∠DGF =∠EGC ，∴△CGE ∽△FGD ，∵EF ⊥CD ，DA =DC ，∴∠DAC =∠DCA =∠DFG =90°-∠FDC ，∴∠ADC =180°-2∠DAC =180°-2(90°-∠FDC )=2∠FDC ．【点评】本题主要考查了全等三角形的判定及性质、相似三角形的判定及性质、菱形的性质等知识点的综合应用，解题时注意：相似三角形的对应角相等，对应边成比例．在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．14(2021秋•宝山区校级月考)如图，四边形DEFG 是△ABC 的内接正方形，AB =BC =6cm ，∠B =45°，则正方形DEFG 的面积为多少？【分析】过A 作AH ⊥BC 于H ，交GF 于M ，于是得到△ABH 是等腰直角三角形，求得AH =BH =2222AB =32cm ，由△AGF ∽△ABC ，得到GF BC =AM AH，求得GF =(62-6)cm ，即可得到结论．【解答】解：过A 作AH ⊥BC 于H ，交GF 于M ，∵∠B =45°，∴AH =BH =22AB =32cm ，∵GF ∥BC ，∴△AGF ∽△ABC ，∴GF BC =AM AH，即GF 6=32-GF 32，∴GF =(62-6)cm ，∴正方形DEFG 的面积=GF 2=(62-6)2=(108-722)cm ．【点评】本题考查了相似三角形的判定与性质，正方形的四条边都相等的性质，利用相似的性质：对应边的比值相等求出正方形的边长是解答本题的关键．15(2021秋•松江区月考)如图，在平行四边形ABCD 中，点E 为边BC 上一点，联结AE 并延长AE 交DC 的延长线于点M ，交BD 于点G ，过点G 作GF ∥BC 交DC 于点F ．求证：DF FC =DM CD．【分析】由GF ∥BC ，根据平行线分线段成比例定理，可得DF FC，又由四边形ABCD 是平行四边形，可得AB =CD ，AB ∥CD ，继而可证得DM AB =DG BG ，则可证得结论．【解答】证明：∵GF ∥BC ，∴DF FC =DG BG，∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，∴DM AB =DG BG ，∴DF FC =DM CD．【点评】此题考查了平行分线段成比例定理以及平行四边形的性质，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．16(2021秋•松江区月考)如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于D ，E 是AC 的中点，DE 的延长线与BC 的延长线交于点F ．(1)求证：FD FC =BD DC ；(2)若BC FC =54，求BD DC的值．【分析】(1)根据直角三角形斜边上中线性质求出DE =EC ，推出∠EDC =∠ECD ，求出∠FDC =∠B ，根据∠F =∠F 证△FBD ∽△FDC ，即可；(2)根据已知和三角形面积公式得出S △BDC S △FDC =54，S △BDF S △FDC =94，根据相似三角形面积比等于相似比的平方得出S △BDFS △FDC =BD DC 2=94，即可求出BD DC．【解答】(1)证明：∵CD ⊥AB ，∴∠ADC =90°，∵E 是AC 的中点，∴DE =EC ，∴∠EDC =∠ECD ，∵∠ACB =90°，∠BDC =90°∴∠ECD +∠DCB =90°，∠DCB +∠B =90°，∴∠ECD =∠B ，∴∠FDC =∠B ，∵∠F =∠F ，∴△FBD ∽△FDC ，∴FD FC =BD DC(2)解：∵BC FC =54，∴S △BDCS △FDC =54，∴S △BDFS △FDC =94，∵△FBD ∽△FDC ，∴S △BDF S △FDC =BD DC2=94，∴BD DC=32．【点评】本题考查了相似三角形的性质和判定，三角形的面积，注意：相似数据线的面积比等于相似比的平方，题目比较好，有一定的难度．17(2021春•黄浦区校级月考)如图，四边形ABCD 是矩形，E 是对角线AC 上的一点，EB =ED 且∠ABE =∠ADE ．(1)求证：四边形ABCD 是正方形；(2)延长DE 交BC 于点F ，交AB 的延长线于点G ，求证：EF •AG =BC •BE ．【分析】(1)根据邻边相等的矩形是正方形即可证明；(2)由AD ∥BC ，推出EF DE =EC EA ，同理DC AG =EC EA，由DE =BE ，四边形ABCD 是正方形，推出BC =DC，可得EFBE =BCAG解决问题；【解答】(1)证明：连接BD．∵EB=ED，∴∠EBD=∠EDB，∵∠ABE=∠ADE，∴∠ABD=∠ADB，∴AB=AD，∵四边形ABCD是矩形，∴四边形ABCD是正方形．(2)证明：∵四边形ABCD是矩形∴AD∥BC，∴EF DE =EC EA，同理DCAG=ECEA，∵DE=BE，四边形ABCD是正方形，∴BC=DC，∴EF BE =BC AG，∴EF•AG=BC•BE．【点评】本题考查相似三角形的判定和性质、矩形的性质、正方形的性质和判定等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．18(2021秋•浦东新区校级月考)如图，在△ABC中，DE∥BC，EF∥CD，求证：AD2=AF•AB．【分析】由DE∥BC，EF∥CD，可得△ADE∽△ABC，△AFE∽△ADC，然后由相似三角形的对应边成比例，证得结论．【解答】证明：∵DE∥BC，EF∥CD，∴△ADE∽△ABC，△AFE∽△ADC，∴AD：AB=AE：AC，AF：AD=AE：AC，∴AD：AB=AF：AD，∴AD2=AF•AB．【点评】此题考查了相似三角形的判定与性质．注意掌握相似三角形的对应边成比例．19(2020秋•浦东新区月考)在△ABC中，D是BC的中点，且AD=AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．(1)求证：△ABC∽△FCD；(2)若DE=3，BC=8，求△FCD的面积．【分析】(1)由DE⊥BC，D是BC的中点，根据线段垂直平分线的性质，可得BE=CE，又由AD=AC，易得∠B=∠DCF，∠FDC=∠ACB，即可证得△ABC∽△FCD；(2)首先过A作AG⊥CD，垂足为G，易得△BDE∽△BGA，可求得AG的长，继而求得△ABC的面积，然后由相似三角形面积比等于相似比的平方，求得△FCD的面积．【解答】(1)证明：∵D是BC的中点，DE⊥BC，∴BE=CE，∴∠B=∠DCF，∵AD=AC，∴∠FDC=∠ACB，∴△ABC∽△FCD；(2)解：过A作AG⊥CD，垂足为G．∵AD=AC，∴DG=CG，∴BD：BG=2：3，∵ED⊥BC，∴ED∥AG，∴△BDE∽△BGA，∴ED：AG=BD：BG=2：3，∵DE=3，∴AG=92，∵△ABC∽△FCD，BC=2CD，∴S△FCDS△ABC=(CDBC)2=14．∵S△ABC=12×BC×AG=12×8×92=18，∴S△FCD=14S△ABC=92．【点评】此题考查了相似三角形的判定与性质以及等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．20(2021春•静安区校级月考)已知：如图，在菱形ABCD中，点E在边BC上，点F在BA的延长线上，BE=AF，CF∥AE，CF与边AD相交于点G．求证：(1)FD=CG；(2)CG2=FG•FC．【分析】(1)根据菱形的性质得到∠FAD =∠B ，根据全等三角形的性质得到FD =EA ，于是得到结论；(2)根据菱形的性质得到∠DCF =∠BFC ，根据平行线的性质得到∠BAE =∠BFC ，根据全等三角形的性质得到∠BAE =∠FDA ，等量代换得到∠DCF =∠FDA ，根据相似三角形的判定和性质即可得到结论．【解答】证明：(1)∵在菱形ABCD 中，AD ∥BC ，∴∠FAD =∠B ，在△ADF 与△BAE 中，AF =BE ∠FAD =∠B AD =BA，∴△ADF ≌△BAE ，∴FD =EA ，∵CF ∥AE ，AG ∥CE ，∴EA =CG ，∴FD =CG ；(2)∵在菱形ABCD 中，CD ∥AB ，∴∠DCF =∠BFC ，∵CF ∥AE ，∴∠BAE =∠BFC ，∴∠DCF =∠BAE ，∵△ADF ≌△BAE ，∴∠BAE =∠FDA ，∴∠DCF =∠FDA ，又∵∠DFG =∠CFD ，∴△FDG ∽△FCD ，∴FD FC=FG FD ，FD 2=FG •FC ，∵FD =CG ，∴CG 2=FG •FC ．【点评】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，菱形的性质，熟练掌握相似三角形的性质是解题的关键．21(2021秋•浦东新区校级月考)如图，梯形ABCD 中，AD ∥BC ，BC =2AD ，点E 为边DC 的中点，BE 交AC 于点F ．求：(1)AF ：FC 的值；(2)EF ：BF 的值．【分析】(1)延长BE 交直线AD 于H ，如图，先由AD ∥BC 得到△DEH ∽△CEB ，则有DH BC =DE CE，易得DH =BC ，加上BC =2AD ，所以AH =3AD ，然后证明△AHF ∽△CFB ，再利用相似比可计算出AF ：FC 的值；(2)由△DEH ∽△CEB 得到EH ：BE =DE ：CE =1：1，则BE =EH =12BH ，由△AHF ∽△CFB 得到FH ：BF =AF ：FC =3：2；于是可设BF =2a ，则FH =3a ，BH =BF +FH =5a ，EH =52a ，接着可计算出EF =FH -EH =12a ，然后计算EF ：BF 的值．【解答】解：(1)延长BE 交直线AD 于H ，如图，∵AD ∥BC ，∴△DEH ∽△CEB ，∴DH BC =DE CE，∵点E 为边DC 的中点，∴DE =CE ，∴DH =BC ，而BC =2AD ，∴AH =3AD ，∵AH ∥BC ，∴△AHF ∽△CFB ，∴AF ：FC =AH ：BC =3：2；(2)∵△DEH ∽△CEB ，∴EH ：BE =DE ：CE =1：1，∴BE =EH =12BH ，∵△AHF ∽△CFB ，∴FH ：BF =AF ：FC =3：2；设BF =2a ，则FH =3a ，BH =BF +FH =5a ，∴EH =52a ，∴EF =FH -EH =3a -52a =12a ，∴EF ：BF =12a ：2a =1：4．【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在运用相似三角形的性质时，主要通过相似比得到线段之间的关系．22(2021秋•浦东新区校级月考)已知：如图，在△ABC 中，BD 是∠ABC 的平分线，过点D 作DE ∥CB ，交AB 于点E ，AD DC =13，DE =6．(1)求AB 的长；(2)求S △ADE S △BCD．【分析】(1)由∠ABD =∠CBD ，DE ∥BC 可推得∠EDB =∠CBD ，进而推出∠ABD =∠EDB ，由此可得BE =DE =6，由DE ∥BC 可得AE EB =AD DC=13，进而证得AE =2，于是可得结论；(2)△ADE 看成以DE 为底，高为h 1，△BCD 看成以BC 为底，高为h 2，由平行线分线段成比例定理和相似三角形的性质可得h 1h 2=AD DE =13，DE BC =14，进而证得结论．【解答】解：(1)BD 平∠ABC ，∴∠ABD =∠CBD ，∵DE ∥BC ，∴∠EDB =∠CBD ，∴∠ABD =∠EDB ，∴BE =DE =6，∵DE ∥BC ，∴AE EB =AD DC =13，∴AE 6=13，∴AE =2，∴AB =AE +BE =8；(2)△ADE 看成以DE 为底，高为h 1，△BCD 看成以BC 为底，高为h 2，∵DE ∥CB ，∴△AED ∽△ABC ，∴h 1h 2=AD DE =13，DE BC =14，∴S △ADE S △BCD =12DE ⋅h 112BC ⋅h 2=112．【点评】本题主要考查了等腰三角形的性质，平行线分线段成比例定理和相似三角形的性质，三角形的面积等知识，熟练应用平行线分线段成比例定理和相似三角形的性质是解决问题的关键．23(2022春•长宁区校级月考)已知：如图，在平行四边形ABCD 中，AC 、DB 交于点E ，点F 在BC 的延长线上，联结EF 、DF ，且∠DEF =∠ADC ．(1)求证：EFBF =AB DB；(2)如果BD 2=2AD •DF ，求证：平行四边形ABCD 是矩形．【分析】(1)由已知条件和平行四边形的性质易证△ADB ∽△EBF ，再由相似三角形的性质：对应边的比值相等即可证明：EF BF =AB DB；(2)由(1)可得BD 2=2AD •BF ，又因为BD 2=2AD •DF ，所以可证明BF =DF ，再由等腰三角形的性质可得∠DEF =90°，所以∠ADC =∠DEF =90°，进而可证明平行四边形ABCD 是矩形．【解答】解：(1)证明：∵平行四边形ABCD ，∴AD ∥BC ，AB ∥DC∴∠BAD +∠ADC =180°，又∵∠BEF +∠DEF =180°，∴∠BAD +∠ADC =∠BEF +∠DEF ，∵∠DEF =∠ADC ，∴∠BAD =∠BEF ，∵AD ∥BC ，∴∠EBF =∠ADB ，∴△ADB ∽△EBF ，∴EF BF =AB DB；(2)∵△ADB ∽△EBF ，∴AD BD =BE BF，在平行四边形ABCD 中，BE =ED =12BD ，∴AD •BF =BD •BE =12BD 2，∴BD 2=2AD •BF ，又∵BD 2=2AD •DF ，∴BF =DF ，∴△DBF 是等腰三角形，∵BE =DE ，∴FE ⊥BD ，即∠DEF =90°，∴∠ADC =∠DEF =90°，∴平行四边形ABCD 是矩形．【点评】本题考查了平行四边形的性质、相似三角形的判断和性质以及矩形的判断，其中(2)小题证明△DBF 是等腰三角形是解题的关键．24(2021秋•宝山区校级月考)已知，如图，在梯形ABCD中，AD∥BC，BC=6，点P是射线AD上的点，BP交AC于点E，∠CBP的角平分线交AC于点F，且CF=13AC时．求AP+BP的值．【分析】延长BF交射线AP于M，根据AD∥BC，根据两直线平行，内错角相等可得∠M=∠CBM，再根据角平分线的定义可得∠PBM=∠CBM，从而得到∠M=∠PBM，根据等角对等边可得BP=PM，求出AP+BP=AM，再根据AC=13CF求出AE=2CF，然后根据△MAF和△BCF相似，利用相似三角形对应边成比例列式求解即可．【解答】解：如图，延长BF交射线AP于M，∵AD∥BC，∴∠M=∠CBM，∵BF是∠CBP的平分线，∴∠PBM=∠CBM，∴∠M=∠PBM，∴BP=PM，∴AP+BP=AP+PM=AM，∵CF=13AC，则AF=2CF，由AD∥BC得，△MAF∽△BCF，∴AMBC =AFCF=2，∴AM=2BC=2×6=12，即AP+BP=12．【点评】本题考查了相似三角形的判定与性质，角平分线的定义，平行线的性质，延长BF构造出相似三角形，求出AP+BP=AM并得到相似三角形是解题的关键，也是本题的难点．25(2020秋•虹口区校级月考)已知：如图，已知△ABC与△ADE均为等腰三角形，BA=BC，DA= DE．如果点D在BC边上，且∠EDC=∠BAD．点O为AC与DE的交点．(1)求证：△ABC∽△ADE；(2)求证：DA•OC=OD•CE．【分析】(1)根据三角形的外角的性质和角的和差得到∠B=∠ADE，由于BABC=DADE=1，根据得到结论；(2)根据相似三角形的性质得到∠BAC=∠DAE，于是得到∠BAD=∠CAE=∠CDE，证得△COD∽△EOA，根据相似三角形的性质得到OCOE =ODOA，由∠AOD=∠COE，推出△AOD∽△COE，根据相似三角形的性质即可得到结论．【解答】证明：(1)∵∠ADC =∠ABC +∠BAD =∠ADE +∠EDC ，∴∠B =∠ADE ，∵BA BC=DA DE =1，∴△ABC ∽△ADE ；(2)∵△ABC ∽△ADE ，∴∠BAC =∠DAE ，∴∠BAD =∠CAE =∠CDE ，∵∠COD =∠EOA ，∴△COD ∽△EOA ，∴OC OE =OD OA，∵∠AOD =∠COE ，∴△AOD ∽△EOC ，∴DA ：CE =OD ：OC ，即DA •OC =OD •CE ．【点评】本题考查了相似三角形的判定和性质，三角形的外角的性质，熟练掌握相似三角形的判定定理是解题的关键．26(2021秋•金山区校级月考)已知：如图，在梯形ABCD 中，AD ∥BC ，点E 在边AD 上，CE 与BD 相交于点F ，AD =4，AB =5，BC =BD =6，DE =3．(1)求证：△DFE ∽△DAB ；(2)求线段CF 的长．【分析】(1)AD ∥BC ，DE =3，BC =6，DF FB =DE BC=36=12，DF DA =DE DB ．又∠EDF =∠BDA ，即可证明△DFE ∽△DAB ．(2)由△DFE ∽△DAB ，利用对应边成比例，将已知数值代入即可求得答案．【解答】证明：(1)∵AD ∥BC ，DE =3，BC =6，∴DF FB =DE BC =36=12，∴DF BD =12，∵BD =6，∴DF =2．∵DA =4，∴DF DA =24=12，DE DB =36=12．∴DF DA=DE DB ．又∵∠EDF =∠BDA ，∴△DFE ∽△DAB ．(2)∵△DFE ∽△DAB ，∴EF AB =DE DB ．∵AB =5，∴EF 5=36，∴EF =52=2.5．∵DE ∥BC ，∴CFEF =BC DE ．∴CF 2.5=63，∴CF =5．(或利用△CFB ≌△BAD )．【点评】此题考查学生对梯形和相似三角形的判定与性质的理解和掌握，第(2)问也可利用△CFB ≌△BAD 求得线段CF 的长，不管学生用了哪种方法，只要是正确的，就要积极地给予表扬，以此激发学生的学习兴趣．27(2020秋•宝山区月考)如图，正方形DEFG 的边EF 在△ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上，已知△ABC 的边BC =15，高AH =10，求正方形DEFG 的边长和面积．【分析】高AH 交DG 于M ，如图，设正方形DEFG 的边长为x ，则DE =MH =x ，所以AM =10-x ，再证明△ADG ∽△ABC ，则利用相似比得到x 15=10-x 10，然后根据比例的性质求出x ，再计算x 2的值即可．【解答】解：高AH 交DG 于M ，如图，设正方形DEFG 的边长为x ，则DE =MH =x ，∴AM =AH -MH =10-x ，∵DG ∥BC ，∴△ADG ∽△ABC ，∴DG BC =AM AH，即x 15=10-x 10，∴x =6，∴x 2=36．答：正方形DEFG 的边长和面积分别为6，36．【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；也考查了正方形的性质．28(2021秋•闵行区校级月考)如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，M 是CD 上的点，DH ⊥BM 于H ，DH 的延长线交AC 的延长线于E ．求证：(1)△AED ∽△CBM ；(2)AE •CM =AC •CD ．【分析】(1)由于△ABC 是直角三角形，易得∠A +∠ABC =90°，而CD ⊥AB ，易得∠MCB +∠ABC =90°，利用同角的余角相等可得∠A =∠MCB ，同理可证∠1=∠2，而∠ADE =90°+∠1，∠CMB =90°+∠2，易证∠ADE =∠CMB ，从而易证△AED ∽△CBM ；(2)由(1)知△AED ∽△CBM ，那么AE ：AD =CB ：CM ，于是AE •CM =AD •CB ，再根据△ABC 是直角三角形，CD 是AB 上的高，易知△ACD ∽△CBD ，易得AC •CD =AD •CB ，等量代换可证AE •CM =AC •CD ．【解答】证明：(1)∵△ABC 是直角三角形，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠CDB =90°，即∠MCB +∠ABC =90°，∴∠A =∠MCB ，∵CD ⊥AB ，∴∠2+∠DMB =90°，∵DH ⊥BM ，∴∠1+∠DMB =90°，∴∠1=∠2，又∵∠ADE =90°+∠1，∠CMB =90°+∠2，∴∠ADE =∠CMB ，∴△AED ∽△CBM ；(2)∵△AED ∽△CBM ，∴AE BC =AD CM，∴AE •CM =AD •CB ，∵△ABC 是直角三角形，CD 是AB 上的高，∴△ACD ∽△CBD ，∴AC ：AD =CB ：CD ，∴AC •CD =AD •CB ，∴AE •CM =AC •CD ．【点评】本题考查了相似三角形的判定和性质、直角三角形斜边上的高所分成的两个三角形与这个直角三角形相似．解题的关键是证明∠A =∠MCB 以及∠ADE =∠CMB ．29(2022秋•徐汇区校级月考)如图，在直角坐标平面内有点A (6，0)，B (0，8)，C (-4，0)，点M 、N 分别为线段AC 和射线AB 上的动点，点M 以2个单位长度/秒的速度自C 向A 方向做匀速运动，点N 以5个单位长度/秒的速度自A 向B 方向做匀速运动，MN 交OB 于点P ．(1)求证：MN ：NP 为定值；(2)若△BNP 与△MNA 相似，求CM 的长；(3)若△BNP 是等腰三角形，求CM 的长．【分析】(1)过点N 作NH ⊥x 轴于点H ，然后分两种情况进行讨论，综合两种情况，求得MN ：NP 为定值53．(2)当△BNP 与△MNA 相似时，当点M 在CO 上时，只可能是∠MNB =∠MNA =90°，所以△BNP ∽△MNA ∽△BOA ，所以AM AN =AB AO ，所以10-2k 5k =106，k =3031，即CM =6031；当点M 在OA 上时，只可能是∠NBP =∠NMA ，所以∠PBA =∠PMO ，根据题意可以判定不成立，所以CM =6031．(3)由于等腰三角形的特殊性质，应分三种情况进行讨论，即BP =BN ，PB =PN ，NB =NP 三种情况进行讨论．【解答】证明：(1)过点N 作NH ⊥x 轴于点H ，设AN =5k ，得：AH =3k ，CM =2k ，①当点M 在CO 上时，点N 在线段AB 上时：∴OH =6-3k ，OM =4-2k ，∴MH =10-5k ，∵PO ∥NH ，∴MN NP =MH OH=10-5k 6-3k =53，②当点M 在OA 上时，点N 在线段AB 的延长线上时：∴OH =3k -6，OM =2k -4，∴MH =5k -10，∵PO ∥NH ，∴MN NP =MH OH=5k -103k -6=53；解：(2)当△BNP 与△MNA 相似时：①当点M 在CO 上时，只可能是∠MNB =∠MNA =90°，∴△BNP ∽△MNA ∽△BOA ，∴AMAN =AB AO，。

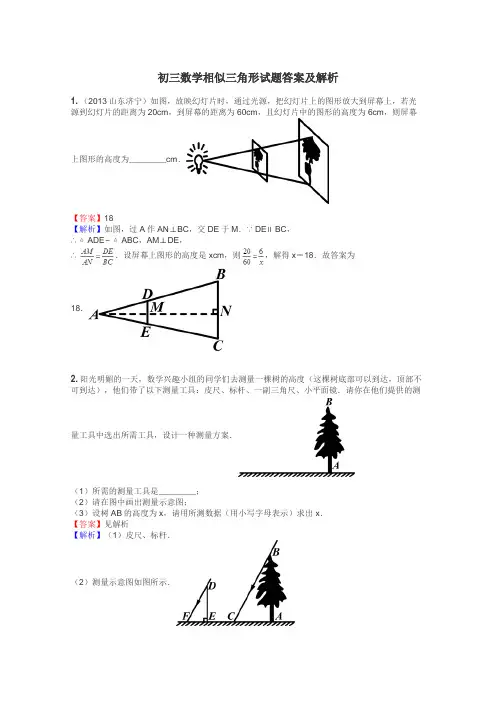
初三数学相似三角形试题答案及解析1.（2013山东济宁）如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为20cm，到屏幕的距离为60cm，且幻灯片中的图形的高度为6cm，则屏幕上图形的高度为________cm．【答案】18【解析】如图，过A作AN⊥BC，交DE于M．∵DE∥BC，∴△ADE∽△ABC，AM⊥DE，∴．设屏幕上图形的高度是xcm，则，解得x＝18．故答案为18．2.阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不可到达），他们带了以下测量工具：皮尺、标杆、一副三角尺、小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是________；（2）请在图中画出测量示意图；（3）设树AB的高度为x，请用所测数据（用小写字母表示）求出x．【答案】见解析【解析】（1）皮尺、标杆．（2）测量示意图如图所示．（3）如图，测得标杆DE＝a，树和标杆的影长分别为AC＝b，EF＝c．∵DF、BC是同一时刻的太阳光线，∴∠DFE＝∠BCA．又∵DE⊥AF，BA⊥AF，∴△DEF∽△BAC，∴，∴，∴．3.（2014山东潍坊）如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内．从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是________米．【答案】54【解析】设建筑物的高为x米，根据题意易得△CDG∽△ABG，∴，∵CD＝DG＝2，∴BG＝AB＝x，再由△EFH∽△ABH可得，即，∴BH＝2x，即BD＋DF＋FH ＝2x，亦即x－2＋52＋4＝2x，解得x＝54，即建筑物的高是54米．4.已知：△ABC∽△A′B′C′，AB＝4cm，A′B′＝10cm，AE是△ABC的一条高，AE＝4.8cm．求△A′B′C′中对应高线A′E′的长．【答案】12cm【解析】∵△ABC∽△A′B′C′．∴．∴．∴A′E′＝12cm．5.两个相似三角形的相似比为2︰5，它们周长的差为9，则较大三角形的周长为________．【答案】15【解析】设较大三角形的周长为x，则较小三角形的周长为x－9，根据周长的比等于相似比可得（x－9）︰x＝2︰5，解得x＝15，即较大三角形的周长为15．6.（2013重庆）已知△ABC∽△DEF，若△ABC与△DEF的相似比为3︰4，则△ABC与△DEF的面积之比为（）A．4︰3B．3︰4C．16︰9D．9︰16【答案】D【解析】相似三角形面积的比等于相似比的平方．7.如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD︰AB＝3︰4，AE＝6，则AC等于（）A．3B．4C．6D．8【答案】D【解析】∵DE∥BC，∴，即，∴AC＝8．故选D．8.如图，△ABC∽△DEF，相似比为1︰2，若BC＝1，则EF的长是（）A．1B．2C．3D．4【答案】B【解析】∵△ABC∽△DEF，相似比为1︰2，∴BC︰EF＝1︰2．∵BC＝1，∴EF＝2．故选B．9.（2014浙江宁波）如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2︰3B．2︰5C．4︰9D．【答案】C【解析】∵AD∥BC，∴∠ACB＝∠DAC．又∵∠B＝∠ACD＝90°，∴△CBA∽△ACD，∴．又∵AB ＝2，DC ＝3，∴，∴．故选C ．10. （2014江苏宿迁）如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，AB ＝8，AD ＝3，BC ＝4，点P 为AB 边上一动点，若△PAD 与△PBC 是相似三角形，则满足条件的点P 个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】∵AD ∥BC ，∠ABC ＝90°，∴∠A ＝90°．设AP 的长为x ，则BP 的长为8－x ．若AB 边上存在P 点，使△PAD 与△PBC 相似，那么分两种情况：①若△PAD ∽△PBC ，则AP ︰BP ＝AD ︰BC ，即x ︰（8－x ）＝3︰4，解得，经检验，其是原方程的解；②若△PAD ∽△CBP ，则AP ︰BC ＝AD ︰BP ，即x ︰4＝3︰（8－x ），解得x ＝2或x ＝6，经检验，它们都是原方程的解．故满足条件的点P 有3个，故选C ．11. （2013安徽）如图，P 为平行四边形ABCD 边AD 上一点，E 、F 分别为PB 、PC 的中点，△PEF ，△PDC ，△PAB 的面积分别为S ，S 1，S 2，若S ＝2，则S 1＋S 2＝________．【答案】8【解析】∵E 、F 分别为PB 、PC 的中点，∴EF 是△PBC 的中位线．∴EF ∥BC ，，∴△PEF ∽△PBC ，∴．∵S ＝2，∴S △PBC ＝8．∴S 1＋S 2＝S △PBC ＝8．12. 若△ABC 与△A′B′C′相似，一组对应边的长为AB ＝6cm ，A′B′＝8cm ，那么△ABC 与△A′B′C′的相似比为________． 【答案】【解析】相似三角形的对应边的比叫做相似比，即相似比为．13. 如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ，AC ＝4，CE＝6，BD＝3，则BF＝（）A．7B．7.5C．8D．8.5【答案】B【解析】∵a∥b∥c，∴，即．∴．∴BF＝BD＋DF＝3＋4.5＝7.5．14.如图，已知在等腰△ABC中，顶角∠A＝36°，BD为∠ABC的平分线，则一定相似的三角形是（）A．△ABC和△BADB．△ABD和△BDCC．△BDC和△ABCD．△ABD和△BDC和△ABC【答案】C【解析】∵∠A＝36°，AB＝AC，∴．又∵BD平分∠ABC，∴∠DBC＝36°．在△BDC和△ABC中，∠DBC＝∠A＝36°，∠C＝∠C，∴△BDC∽△ABC．故选C．15.在△ABC与△A′B′C′中，AB︰AC＝A′B′︰A′C′，∠B＝∠B′，则这两个三角形（）A．相似，但不全等B．全等或相似C．不相似D．无法判定是否相似【答案】D【解析】因为AB︰AC＝A′B′︰A′C′，∠B＝∠B′，条件中相等的角不是成比例的两边的夹角，所以无法判定是否相似，故选D．16.如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（）A．B．∠C＝∠AEDC．∠B＝∠DD．【答案】D【解析】由∠1＝∠2可得∠DAE＝∠BAC，但条件与∠DAE＝∠BAC不是成比例的两边与夹角的关系，故不能判定三角形相似．17.如图，点P是△ABC的边AC上一点，连接BP，以下条件中，不能判定△ABP∽△ACB的是（）A．B．C．∠ABP＝∠CD．∠APB＝∠ABC【答案】B【解析】△ABP和△ACB有公共角∠A，故添加，由“两边成比例且夹角相等的两个三角形相似”可得△ABP∽△ACB；添加∠ABP＝∠C或∠APB＝∠ABC，由“两角分别相等的两个三角形相似”可得△ABP∽△ACB；只有添加不能得出△ABP∽△ACB．故选B．18.（2014河北）在研究相似问题时，甲、乙同学的观点如下：对于两人的观点，下列说法正确的是（）A．两人都对B．两人都不对C．甲对，乙不对D．甲不对，乙对【答案】A【解析】由题意知新三角形与原三角形的对应角相等，对应边的比也相等，所以两个三角形相似，甲的观点正确；新矩形与原矩形的对应角相等，但对应边的比并不相等，所以新矩形与原矩形不相似，乙的观点也正确．故选A．19.如图，已知△ABC中，D为边AC上一点，P为边AB上一点，AB＝12，AC＝8，AD＝6，当AP的长为________时，△ADP和△ABC相似．【答案】4或9【解析】当△ADP∽△ACB时，需有，∴，解得AP＝9．当△ADP∽△ABC时，需有，∴，解得AP＝4．∴当AP的长为4或9时，△ADP和△ABC相似．20.如图，点A，B的坐标分别是（0，8），（6，0），过边OA上的点P（0，4）作直线PQ与△OAB的另一边相交于点Q，当点Q的坐标为________时，形成的新三角形与△OAB相似．【答案】（3，4）或（3，0）或（1.92，5.44）或（，0）【解析】由已知得OA＝8，OB＝6，OP＝4，由勾股定理可得AB＝10．①当PQ∥x轴时，△APQ∽△AOB，此时Q是AB的中点，可得Q（3，4）．②当PQ∥AB时，△OPQ∽△OAB，此时点Q是OB的中点，可得Q（3，0）．③当PQ⊥AB于Q时，由，可得△APQ∽△ABO，则，解得AQ＝3.2．此时，作QC⊥OA于C，可得△AQC∽△ABO，，即，解得AC＝2.56，QC＝1.92，∴OC＝8－2.56＝5.44，∴点Q（1.92，5.44）．④当时，△OPQ∽△OBA，则，解得，∴Q（，0）．故点Q的坐标为（3，4）或（3，0）或（1.92，5.44）或（，0）．。