下载文档原格式
用主成分分析模型构造中学考试综合评价指数[摘要] 在中学考试的综合评价中，使用较多的指标进行描述使分析复杂化，难以对众多指标的影响作出正确的判断，需要少量几个“综合评价指标”。
通过简单加权的合成方法，难以得到科学的结果。
主成分分析是一种多元统计方法，可以将众多指标简化浓缩为少量几个甚至一个综合评价指标，使简化的指标既能基本包括全部指标具有的信息，又使指标之间相互无关，较好地解决了这一课题。
[关键词] 考试评价；主成分分析；数学模型；计算步骤，指数构造方法一、问题的提出在中学考试评价中，通常使用各学科的“平均分”、“优秀率”、“及格率”和“低分率”等指标。
考虑到成绩的分布状况（“优秀率”与“及格率”之间的差距偏大，可能失去部分信息量），某些地区还使用了“良好率”指标。
这样，k 个学科的考试评价的p 项指标将多达k ╳p 个。
在对考试进行综合的评价时，使用较多的指标进行描述不仅会增加评价的工作量，而且会因评价指标间的相关性造成评价信息重叠，相互干扰，其结果使分析复杂化，难以对众多指标的影响作出正确的判断。
因此，需要少数几个甚至一个“综合评价指标”来代替众多的且相互之间具有相关关系的指标，同时又需要不失去原有指标具有的信息量，这是考试评价中具有现实意义的课题。
某些地区采用一种“降维”的方法，较成功地把k ╳p 维指标降为p 维指标，即在使用“总分平均分”的同时，用“科平均╳╳率”取代各科的“╳╳率”（计算方法见备注1）。
如何把p 维指标再合成为一个“综合评价指标”？采用一些简单加权的合成方法时，由于对各指标的影响不容易作出正确的定量化的判断，及权数产生的科学性等问题，往往难以得到令人信服的科学的结果。
主成分分析是一种多元统计方法，可以将众多指标简化浓缩为少数几个甚至一个综合评价指标，使简化的指标既能基本包括全部指标具有的信息，又使指标之间相互无关。
较好地解决了这一课题。
二、主成分分析的数学模型设有n 个样品，每个样品观测p 个指标（变量）：X 1，X 2，…，X p , 得到原始数据矩阵：用数据矩阵X 的p 个列向量（即p 个指标向量）作线形组合（即综合指标向量）为：上述方程组要求：且系数αij 由下列原则决定：①、F i 与F j （i ≠j ，i ，j =1，…，p ）不相关；②、F 1是X 1，X 2，…，X p 的一切线性组合（系数满足上述方程组）中方差最大的，F 2是与F 1不相关的X 1，X 2，…，X p 的一切线性组合中方差最大的，…，F p 是是与F 1，F 2，…，F p-1都不相关的X 1，X 2，…，X p 的一切线性组合中方差最大的。
基于主成分分析法的学⽣成绩评价与分析-最新教育⽂档
基于主成分分析法的学⽣成绩评价与分析
2.运⽤主成分分析法对学⽣成绩进⾏综合评价与分析
以周⼝师范学院数学系45名学⽣在2013―2014学年的考试科成绩为例，把45名学⽣成绩作为⼀个整体，把9科考试科⽬作为变量，分别⽤X1，X2，…，X9来表⽰。
为科学评价学⽣的成绩，以各科学时除以总学时作为该科权重，再乘以此课程的原始成绩。
利⽤SPSS软件将原始数据标准化，并求出该矩阵的相关系数矩阵Q。
计算矩阵Q的特征值，得到各主成分的⽅差贡献率和累计⽅差贡献率。
累计贡献率达到80%以上的主成分系数有四个，所以可得出关系如下。
将标准化处理以后得到的数据分别代⼊到以上各个式⼦中，这样就可以得到样本在G1，G2，G3，G4，G上的得分及综合排名。
由以上分析可以知第⼀主成分对泛函分析解释⽐较充分，表⽰数学抽象理解能⼒；第⼆主成分对运筹学解释⽐较充分，作为学⽣的计算能⼒指标；第三主成分对⽑中特代表较⼤为学⽣对于时事政治⽅⾯的关注程度；第四主成分对于数学教学论解释较⼤，表⽰学⽣作为师范⽣所必须具备的实际课堂教学技能⽅⾯的能⼒。
２０１９.３江苏外语教学研究基于主成分分析法(ＰＣＡ)的大学英语考试成绩综合评定王㊀辉(广东财经大学华商学院)㊀㊀摘要:英语是一门语言ꎬ仅仅通过期末考试成绩很难科学地评定学生的英语水平ꎮ为了使考试成绩评定更加科学合理ꎬ本文提出了一种基于主成分分析(ＰＣＡ)的成绩综合评定方法ꎮ首先以考试试题各项目满分值为基础对各分项目的成绩进行归一化处理ꎬ然后利用主成分分析方法求取各项目的权值系数ꎬ最后对各项目的分数进行综合评定得出综合成绩ꎬ作为学生的最终成绩ꎮ研究表明ꎬ本文所提出的方法能够有效地反映考试中难度最大和得分最离散项目的影响ꎬ与各项直接相加所得的成绩相比ꎬ综合成绩更加科学合理ꎬ也更能够反映不同考生的学习水平ꎮ关键词:考试成绩ꎻ归一化ꎻ主成分分析０.引言考试成绩是衡量学生学习情况的重要指标ꎬ也是教师教学效果的重要反映ꎮ准确㊁客观㊁全面㊁科学地评价考生的学业综合成绩对考生和教师来说都是非常重要的ꎮ目前大部分高校采取传统的评价方法ꎬ即以考试总分或学分绩点作为评价学生综合成绩的手段ꎮ但是ꎬ知识本位观影响下的教学评价内容狭窄ꎬ仅仅着眼于学生对知识掌握的多少及精确度ꎮ(李光梅ꎬ２００７)如何科学地评价学生的成绩这个话题是国际上共同关心的话题ꎮ学生考试成绩不应该仅以分数论高低ꎬ学生成绩应该体现学生在本学科多方面的水平ꎮ美国采用ＣＡＡＰ(ＣｏｌｌｅｇｉａｔｅＡｓｓｅｍｅｎｔｏｆＡｃａｄｅｍｉｃＰｒｏｆｉ￣ｃｉｅｎｃｙ)及ＣＬＡ(ＣｏｌｌｅｇｉａｔｅＬｅａｒｎｉｎｇＡｓｓｅｓｓｍｅｎｔ)测试ꎬ其共同测试内容就包括了批判性思维㊁阅读能力㊁写作能力ꎮ(赵婷婷ꎬ２０１５)英语作为一门语言ꎬ其掌握水平需要学生听说读写译各方面能力的展现ꎬ而课程考试的成绩并不能完全体现出学生的水平ꎮ例如ꎬ有的学生平常课堂上体现出的英语水平跟英语考试分数并不能成正比ꎮ因此ꎬ本文采用主成分分析法来对考生成绩进行科学的评价ꎮ将试题各个项目通过ＰＣＡ计算分析ꎬ最终得出能体现学生真实的英语水平的成绩ꎮ１.研究方法本研究方法的原理如图１所示ꎬ首先对试题各项分数进行归一化处理ꎬ然后利用主成分分析方法(ＰｒｉｎｃｉｐａｌＣｏｍｐｏｎｅｎｔＡｎａｌｙｓｉｓꎬＰＣＡ)计算得出各主成分的系数ꎬ最后根据各项系数计算得出新成绩ꎮ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀各项分数归一化ң㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ＰＣＡ分析求权值系数ң㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀计算新成绩图１㊀方法的原理１.１㊀成绩归一化试题通常由多个分项构成ꎬ英语考试常见的分项有听力㊁词汇㊁填空㊁阅读㊁翻译㊁作文等ꎬ各个分项的满分不同ꎮ在改卷时一个项目通常由一组判卷尺度相近的教师审阅ꎬ为了消除各项满分不同和教师判卷给分尺度不同所造成的影响ꎬ需要对各项分数进行归一化处理ꎮ设一次考试试题有ｎ个项目ꎬ每个项目的满分为Ｍｉ(ｉ＝１ꎬ ꎬｎ)ꎬ总共有ｍ位考生参加了考试ꎬ则由考生成绩构成的矩阵Ｙ＝(ｙ１ꎬｙ２ꎬ ꎬｙｎ)为一个ｍ行ｎ列的矩阵ꎬ其每一行表示一位考生的ｎ个项目的成绩ꎬ其每一列ｙｉ表示ｍ位考生某一项的成绩ꎬ则归一化处理方法为:ｘｉ＝ｙｉ/Ｍｉ(ｉ＝１ꎬ ꎬｎ)(１)这种归一化方法有两个好处:一是有效地消除了教师改卷时给分尺度的问题ꎬ将尺度统一化ꎻ二是有效地消除各项满分不同所造成的差别ꎮ１.２㊀权值系数求取在实际中ꎬ很多观测变量并不是相互独立的ꎬ部分变量包含了相同的信息ꎬ主成分分析的目的主要有三方面:一㊁提取数据中最重要的信息ꎻ二㊁去除不重要的信息ꎬ以简化压缩数据ꎻ三㊁决定变量的重要程度与相互关系ꎮ(ＡｂｄｉꎬＷｉｌｌｉａｍｓꎬ２０１０ꎻＷｏｌｄꎬ１９８７)主成分分析通过对输入变量进行线性组合ꎬ生成一系列正交的主成分ꎬ并按照变量的变化速度大小进行排序ꎮ对考生成绩进行主成分分析ꎬ求取主成分系数的过程如下:首先ꎬＸ＝(ｘ１ꎬｘ２ꎬ ꎬｘｎ)ꎬＣ＝ｃｏｖ(ｘ１ꎬｘ１)ｃｏｖ(ｘ２ꎬｘ１) ｃｏｖ(ｘｎꎬｘ１)ìîíïïïï式(２)中ｃｏｖ(ｘｉꎬｘ于ｃｏｖ(ｘｉꎬｘｊ)＝ｃｏｖ(ｘｊＪｉａｎｇｓｕＦｏｒｅｉｇｎＬａｎｇｕａｇｅＴｅａｃｈｉｎｇａｎｄＲｅｓｅａｒｃｈ２０１９.３然后ꎬ求协方差矩阵的特征值ꎬ求特征值的方程为:λＩ－Ｃ＝０(３)式(３)中Ｉ为单位矩阵ꎮ当求出特征值λｉ(ｉ＝１ꎬ２ꎬ３ꎬ ꎬｎ)之后ꎬ将其按从大到小的顺序进行排列(即λ１ȡλ２ȡ ȡλｎ)ꎮ之后ꎬ求取各主成分的权值系数和累计贡献率ꎬ权值系数最大的主成分通常包含了数据中最重要的信息ꎬ主成分的权值系数ｒｉ和累计贡献率Ｌ的计算式为:ｒｉ＝λｉ/ðｎｉ＝１λｉ(４)Ｌ＝ðｋｉ＝１λｉ/ðｎｉ＝１λｉ(ｋɤｎ)(５)式(５)中Ｌ表示前ｋ个主成分的累计贡献率ꎬ通常要求主成分的累计贡献率不低于８０％ꎮ最后ꎬ分别求取从大到小的ｋ个特征值λｉ(ｉ＝１ꎬ ꎬｋ)所对应的正交单位化特征向量ｅｉ(ｉ＝１ꎬ ꎬｋ)ꎬ设Ｒ＝[ｒ１ꎬｒ２ꎬ ꎬｒｋ]ＴꎬＥ＝[ｅ１ꎬｅ２ꎬ ꎬｅｋ]ꎬ则各分项的权值系数矩阵为:Ｆ＝ＥＲ(６)１.３㊀综合成绩评定利用归一化处理之后的成绩Ｘ和各分项的权值系数Ｆ计算综合成绩系数:Ｐ＝ＸＦ(７)由于前文对成绩进行了归一化处理ꎬ因此公式(７)计算得出的为分布在０~１之间的综合成绩系数ꎬ为了使综合评定成绩的量纲与原成绩保持一致ꎬ按下式计算综合成绩:Ｚ＝ｋ Ｐ(８)公式(８)中ｋ＝ðｎｉ＝１Ｍｉꎬ为各项目的满分之和ꎬ即试卷的总分ꎮ２.研究数据及结果２.１㊀研究数据本研究以广州某独立学院２０１６级大学英语成绩作为数据来源ꎬ选取了工商㊁金融㊁会计三个班共１２２位考生某次期末英语考试的成绩ꎬ其中工商班４０位考位考生ꎬ所有班级考㊁词汇㊁填空㊁阅读㊁２５㊁１０㊁１０㊁Ｙ为１２２行Ｙ进行归一化处理ꎬ最低ꎬ表明听力项是本次考试中难度最大㊁最难得分的一项ꎬ填空项平均归一化成绩最高ꎬ表明填空项是本次考试中最容易得分的一项ꎬ按照难度从大到小排列的顺序依次为听力㊁阅读㊁词汇㊁作文㊁翻译㊁填空ꎮ表１㊀各项的平均归一化成绩项目听力词汇填空阅读翻译作文平均归一化成绩０.４７０.７００.８６０.６３０.８４０.７５㊀㊀归一化后的成绩Ｘ的６个分项目的标准差如表２所示ꎬ标准差越大表示考生在该项目得分的离散程度越大ꎬ从表２中可以看出词汇的标准差最大ꎬ表明词汇项的分数分布最离散ꎮ表２㊀各项分数的标准差项目听力词汇填空阅读翻译作文标准差０.１３５０.２７９０.１９７０.１５５０.１８００.１２７㊀㊀然后ꎬ计算各主成分的累计贡献率ꎬ计算发现前４个主成分的累计贡献率为８４％ꎬ因此取前４个主成分进行分析ꎮ进而按照公式(６)计算各项目的权值系数ꎬ如表３所示ꎬ从表３中可以看出ꎬ各项权值系数从大到小排列依次为听力项㊁词汇项㊁翻译项㊁填空项㊁阅读项和作文项ꎬ其中听力项的权值最大ꎬ表明听力项最难最重要ꎬ听力对综合成绩的影响也最大ꎬ这与表１的分析结果一致ꎮ此外ꎬ词汇项的权值系数也较大ꎬ主要是因为词汇项的离散程度最大ꎬ离散程度越大的项目越容易区分出不同学生的学习水平ꎮ表３㊀各分项的权值系数听力项词汇项填空项阅读项翻译项作文项０.３２４０.２４７０.１０７０.０６１０.２２１０.０５１㊀㊀最后ꎬ按照公式(８)计算得到各位考生的综合成绩ꎮ综合成绩与原成绩的对比如图２所示ꎬ与原成绩相比综合成绩的分布更为分散ꎬ最高分由原成绩的９１提高到了９４.７ꎬ最低分由原成绩的４４降低到了３７ꎬ更加分散的成绩分布则更容易区分不同考生的水平ꎮ图２㊀综合成绩与原成绩的对比２.３㊀研究结果原成绩中８０分至１００分的１０位高分考生的原成２０１９.３江苏外语教学研究绩与综合成绩的对比如表３所示ꎬ从表中可以看出ꎬ原成绩中编号为４３的考生的成绩最高ꎬ而其综合成绩也最高ꎻ原成绩高于８０分的考生ꎬ他们的综合成绩也都高于８１.４分ꎬ表明本文介绍的方法不会埋没成绩优秀的考生ꎮ表３㊀１０位高分考生的原成绩与综合成绩的对比考生编号１６１９３９４３６３６５６６９１９８１２２原成绩８０８１８５９１８０８３８９８１８６８２综合成绩８１.４８４.１８６.１９４.７８５.６８７.６９１.１８４.９８７.３８８.１㊀㊀编号为１６和６３的两位考生ꎬ他们的原成绩都为８０分ꎬ从原成绩中无法区分两位考生的英语水平ꎬ而他们的综合成绩分类为８１.４分和８５.６分ꎬ存在明显的差别ꎻ编号为３９和１２２的两位考生的原成绩分别为８５分㊁８２分ꎬ考生３９的原成绩较高ꎬ而其综合成绩却低于考生１２２的综合成绩ꎮ以上４位考生的各项成绩如表４所示ꎬ从表中可以看出ꎬ考生１６的听力㊁词汇项得分都低于考生６３ꎬ而听力为本次考试中考生得分困难的一项ꎬ其在综合成绩中的权值系数也最大ꎬ并且词汇项的权值系数也较大ꎬ因此考生１６的综合得分低于考生６３ꎮ考生３９的听力㊁词汇㊁翻译㊁填空这四项权值系数最大的项目的得分都不高于考生１２２ꎬ因此其综合成绩低于考生１２２ꎮ表４㊀４位高分考生的各项成绩考生编号听力词汇填空阅读翻译作文原成绩综合成绩１６１５８１０２４１０１３８０８１.４６３１７９１０２３１０１１８０８５.６３９１６１０１０２６９１４８５８６.１１２２１７１０１０２５１０１０８２８８.１㊀㊀原成绩中低于５０分的８位低分考生的原成绩与综合成绩的对比如表５所示ꎬ从表５中可以看出ꎬ这８位原成绩低于５０分的考生ꎬ他们的综合成绩也不高于５６分ꎮ表５㊀８位低分考生的原成绩与综合成绩的对比考生编号１３６１７４１０９１１６１１７１１８原成绩４４４５４５４９４６４７４６４６综合成绩４７.９４１.２３７.０４８.６５６.０４２.９４２.５４３.４㊀㊀考生１０９的原成绩低于考生７４ꎬ而其综合成绩却得到了５６分ꎬ高于考生７４ꎮ这两位考生的各项成绩如表５所示ꎬ从表中可以看出ꎬ对于权值系数最大的四项 听力㊁词汇㊁翻译㊁填空ꎬ两位考生听力项的得分相同ꎬ翻译和词汇两项的权值系数相近ꎬ虽然考生１０９词汇项得分比考生７４少４分ꎬ但是考生１０９翻译项得分比考生７４高８分ꎬ并且考生１０９填空项得分比考生７４高ꎬ因此考生１０９比考生７４的综合得分高ꎮ表６㊀２位低分考生的各项成绩考生编号听力词汇填空阅读翻译作文原成绩综合成绩７４１０８５１５２９４９４８.６１０９１０４６６１０１０４６５６.０３.结语通过数据分析ꎬ可得出以下结论:(１)以主成分分析方法重新计算学生学习成绩ꎬ由综合成绩可以看出ꎬ原成绩高的学生综合成绩也高ꎬ原成绩低的学生综合成绩也没有太大改变ꎮ这说明ꎬ主成分分析得出的成绩对学生原成绩的影响并不太大ꎮ(２)本文所提出的基于主成分分析的综合评分法中ꎬ考试难度最大的项目是听力题ꎬ得分最离散的项目是词汇题ꎬ这两项对综合得分影响最大ꎮ按照多数学者的观点及学生自身的反映ꎬ听力和词汇确实属于相对较难的题型ꎮ以此来看ꎬ主成分分析方法比普通的直接相加计算总分的方法更加科学合理ꎮ此分析结果或许能为以后的英语教学提供一点启示ꎬ在教学中要注重听力和词汇的教学ꎬ学生也要加强听力和词汇方面的学习ꎮ同时ꎬ本文的方法能够为其他课程考试成绩的评定以及多课程的综合成绩的评定提供些许参考ꎮ参考文献[１]ＡｂｄｉＨꎬＷｉｌｌｉａｍｓＬＪ.Ｐｒｉｎｃｉｐａｌｃｏｍｐｏｎｅｎｔａｎａｌｙｓｉｓ[Ｊ].Ｗｉｌｅｙ２０１０(４):４３３４５９.[２]ＷｏｌｄＳꎬＥｓｂｅｎｓｅｎｓｉｓ[Ｊ].１９８７(２):３７５２.[３]李光梅.[４]赵婷婷.大学生学究ꎬ２０１５.[作者信息]王㊀辉㊀ｉｂｅｌｉｅｖｅ＠１２６.ｃｏｍ。
主成分分析法在学生成绩分析与评价中的应用*郭兰兰1，付政庆2*，衣秋杰1（1.山东科技大学机械电子工程学院，山东青岛266590；2.山东科技大学数学与系统科学学院，山东青岛266590）引言在高等教育教学过程中，教学与考试都是非常重要且相互联系不可分割的，考试本身也可以看做一种教学活动[1]。
各个高校都非常重视使用考试手段对教育质量进行检测和监控，规范和引导教师的教学行为；激励学生努力地学习、培养他们分析问题和解决问题的能力[2]。
因此，考试成绩是能够体现学生在校学习情况的主要因素。
而对于阶段性的评价，经过分析后得到一些对以后非常有用的信息，所以对学生成绩进行分析评价有着重要的意义[3]。
采用多元统计分析的方法对这些信息认真研究，可以充分挖掘考试结果的数据，得到隐藏在学生考试成绩中的有用信息，为提高教学质量提供重要的依据[4]。
本文中，运用主成分分析法对某高校数学专业学生的成绩进行深入分析，得到了影响学生成绩的几个关键因素，并在此基础上对学生的学习特点进行了深入研究。
一、统计分析方法在对实际问题的研究过程中，影响因素往往不止一个，为了更加全面系统，通常这些因素都要考虑，这些因素即为研究的指标[5]。
每个指标或者因素都可以不同程度上反映问题的某些信息，这导致所反映的信息就会产生一定的重合，即各个原始指标之间往往会有一定的相关性。
采用统计方法分析多指标问题时，指标个数太多使问题的复杂程度大大增加。
在研究实际问题时，尽量通过较少的指标反映问题尽量多的信息[6]。
主成分分析法的基本思想为：对问题的原始指标做线性组合形成综合指标，按方差大小进行排序，选取前几个综合指标，依次定义为第一、第二、第三主成分等等。
这些主成分间是线性无关的。
这样处理，既能降低问题的复杂度，又能从原始数据中进一步挖掘实际问题的某些新信息[7-8]。
在实际问题中，为了降低分析的难度，提高分析效率，通常不直接对原始指标（p个）构成的随机向量x=（x1，x2，…，x p）进行分析，而是先对向量做线性变换，把原来的随机向量变换成新的综合变量y1，y2，…，y p。
基于主成分分析法的学生成绩综合评价
摘要：以贵州航天职业技术学院2011级社区管理与服务班在2011—2012学年的13门主要课程考试成绩为研究对象，借助统计软件进行主成分分析，计算出主成分得分，并按主成分得分对学生进行了排名。
为使成绩评价更具科学性、客观性和合理性，还将平均分和综合分比对，进行综合评价与分析，为教学研究、学生管理及就业指导提供科学依据。
关键词：主成分分析法；学习成绩；评价
中图分类号：g455 文献标识码：a 文章编号：1001-828x（2013）07-0-03
一、引言
在经济全球化和社会分工越来越细化的当今社会，人力资源已成为人类的第一宝贵资源。
作为高素质人才主要培养基地的高等院校，如何科学地评价大学生的综合成绩成为当前各高校在全面推进素质教育过程中所面临的问题之一。
传统的以多门课程总平均分排名的评价方法，比较笼统，为了尽可能全面、科学地反映被评价对象的情况，往往需要选取众多的指标构成评价体系，但是，过多的指标不仅会增加评价的工作量，还会因评价指标间的相关性造成评价信息相互重叠、相互干扰，从而难以客观地反映被评价对象的真实水平。
本文认为可以使用主成分分析法解决此类问题。
二、主成分分析方法简介
主成分分析，是利用降维的方法，将多个指标转化为少数几个综
合指标，去解释原始资料中的大部分变异的一种方法。
在实际问题中，为了全面、系统地分析问题，通常必须考虑众多的影响因素，这些影响因素一般被称为指标或者变量。
因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而反映的信息在一定程度上有重叠。
在用统计方法研究多变量问题时，变量太多会增加计算量和分析问题的复杂性，人们希望在进行定量分析的过程中，涉及的变量较少，得到的信息量较多。
因此，把这些变量转化成彼此不相关的变量，然后从中选出比原始变量个数少、却能解释原始资料中大部分变异的几个新变量，即所谓的主成分，从而达到降维和简化问题分析的目的。
具体而言，主成分分析法是通过数学变换把给定的一组相关变量通过线性变换转成另一组不相关的变量，并按方差依次递减的顺序排列，找到第一、第二、…第 k个主成分，然后计算因子载荷矩阵，建立主成分模型，最后按因子得分及贡献率的大小，计算综合得分并进行排序。
三、高校学生成绩综合评价应用
（一）研究的对象及指标的选择
本文以贵州航天职业技术学院11级社区管理与服务班在2011—2012学年的13门主要课程考试成绩为研究对象，借助统计软件进行主成分分析，计算出主成分得分，并按主成分得分对学生进行了排名。
班上共有28名同学，将这28名同学作为总体，13门主要课程具体为：大学英语ⅰ（x1）、思想道德修养与法律基础（x2）、管
理学原理（x3）、社区管理学（x4）、社会工作法律实务（x5）、应用统计学（x6）、体育（x7）、社会心理学（x8）、服务礼仪（x9）、高等数学（x10）、团队建设（x11）、大学英语ⅱ（x12）、大学语文（x13），学生姓名用序号1、2、… 28表示，用xij 表示第i个同学在第j 门课上的得分，则x=（xij）28×l3，这样就得到了一个28×13的原始数据矩阵。
见表1。
（二）主成分分析过程
将原始数据标准化，用计算机求出标准化矩阵的相关系数矩阵；求相关矩阵的特征值，确定主成分个数。
（见表2）
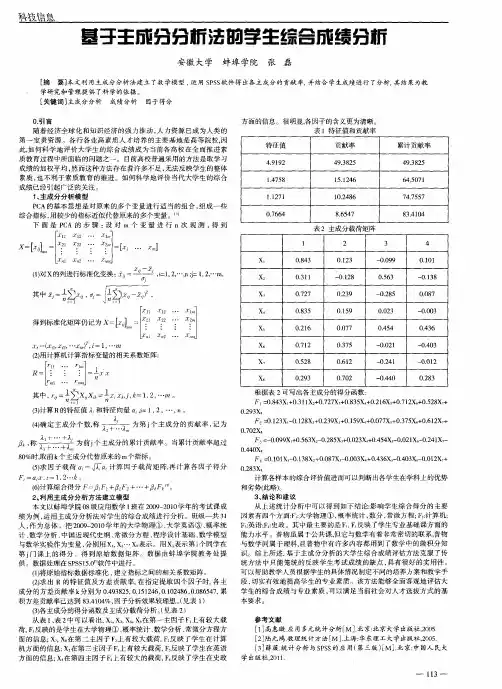
表2 方差分解主成分提取分析表
如表2所示，将13个主成分按照特征根从大到小的次序排列，可以看出第一主成分的特征根为5.984，它解释了总变异的
46.352%；第二主成分的特征根为1.617，它解释了总变异的
12.683%；第三主成分的特征根为1.382，它解释了总变异的
11.476%；第四主成分的特征根为1.134，它解释了总变异的9.556%，因此，前4个主成分的累计贡献率已经达到80.067%，即前4 个主成分可以反映13个指标80.067%的信息量，说明只取前4个主成分即可。
上述13 项指标可以综合成4个公共因子（f1、f2、f3 和f4），并可得到因子载荷矩阵（表3）。
表3 因子载荷矩阵
从表3可以看出：第一主成分在x3、x4、x5、x6、x8、x10、x11
上有较大载荷，f1反映的是学生在管理学、社区管理学、社会工作法律实务、应用统计学、社会心理学、高等数学、团队建设方面的信息，故可以认为第一主成分是说明学生专业知识的学习情况；第二主成分在x2、x13上有较大载荷，f2反映的是学生在思想道德修养与法律基础、大学语文方面的信息，故可以认为第二主成分是说明学生基础知识的学习情况；第三主成分在x7上有较大载荷，f3反映的是学生在体育方面的信息，故可以认为第三主成分是说明学生体育运动方面的情况；第四主成分在x9上有较大载荷，f4反映的是服务礼仪方面的信息，因此可以认为第四主成分是说明学生在交际礼仪方面的情况。
计算各个主成分的得分：
f1=0.2865x1+0.1276x2+0.3260x3+0.3675x4+0.3762x5+0.2711x 6-0.1798x7+0.3502x8+0.2113x9+0.3205x10+0.3063x11+0.2117x1 2-0.0136x13
f2=-0.2335x1+0.5682x2-0.1802x3-0.1065x4-0.1418x5-0.2198 x6-0.3501x7-0.0123x8+0.2177x9-0.1055x10+0.1182x11+0.4782x 12+0.2408x13
f3=0.1927x1-0.0909x2-0.1206x3+0.0922x4-0.0672x5-0.1326x 6+0.4301x7+0.0912x8-0.2786x9+0.2721x10+0.0059x11+0.2231x1 2+0.7065x13
f4=-0.2876x1+0.7285x2-0.2251x3-0.1353x4-0.1765x5-0.2755 x6-0.4256x7-0.0156x8+0.2716x9-0.1346x10+0.1519x11+0.5976x
12+0.3129x13
根据以上四个表达式求出各主成分得分后，以特征值的贡献率作为加权系数求出综合得分：
f=0.46352f1+0.12683f2+0.11476f3+0.09556f4
由此得到学生成绩的综合排名详见表4。
表4 综合排名
（三）评价
经主成分分析，在基本保留原始数据信息量的前提下，将l3个具有一定相关性的原始指标降维成4个相对独立的主成分，这4个主成分可以代表13个指标80.067%的信息量。
从表4可以看出，通过主成分分析法得到的综合分排名与平均分排名基本相符，但也存在一定的差距。
如20号同学综合分排名是第6名，而平均分排名是第16名，主要原因是他在第一主成分上得分较高，说明该同学专业知识学得比较扎实，其专业能力相对较强；而22号同学则刚好相反，其综合分排名是第19名，平均分排名是第12名，主要原因是他在第一主成分上得分较低，恰恰第一主成分是考察社区管理专业学生的关键，它反映了学生专业素质方面的水平，因此要建议该同学提高认识，加强专业知识的学习，努力提高专业素质。
又如平均分很接近的3号、11号、26号三位同学，平均分排名均为第9、第7、第8名，综合分排名分别为第8、第5、第3名，从表4看出26号同学在第一和第二主成分上得分比3号和11同学号要高，表明26号同学在专业知识和基础知识方面有优势， 26号
同学在三个主成分上得分均为正，因此综合得分高出3号和11号；虽然3号在第三主成分上得分均高于11号和26号同学，但是第三主成分的贡献率仅为11.476%，无法取代11号、26号同学在第一主成分上的优势，因此他的综合分排名仍在11号、26号同学之后。
四、结论
本文运用主成分分析法，评价了大学生的综合成绩，克服了传统方法中只能笼统反映学生考试成绩的缺点，分析的结果可以客观地反映学生各方面知识的掌握情况，了解学生的优、劣势，帮助教学人员因材施教，做到有针对性地指导学生发挥优势，弥补劣势，为教学研究、学生管理及就业指导提供科学依据。
参考文献：
[1]向定峰.高职学生成绩的因子分析[j].重庆教育学院报，2007（03）：24-27.
[2]李曦.多元统计在学生成绩分析的运用[j].南昌航空工业学
院学报·自然科学版，2006（033）：58-62.
[3]管宇.实用多元统计分析[m]杭州：浙江大学出版社，2011.
[4]扬宇音，赵雅明，曲立敏.因子分析法在大学生综合排名中的应用[j].贵州工业大学学报，2005，34（01）：9-12.。
