第六讲判别分析ppt课件

格式：ppt
大小：2.01 MB
文档页数：89

下载文档原格式

什么是判别分析63页PPT

这里应该注意到，当 Σ I （单位矩阵）时，即为欧氏距离
的情形。
二、距离判别的思想及方法
1、两个总体的距离判别问题
问题：设有协方差矩阵∑相等的两个总体G1和G2，其均值
分别是1和 2，对于一个新的样品X，要判断它来自哪个总
体。
一般的想法是计算新样品X到两个总体的马氏距离D2（X， G1）和D2（X，G2），并按照如下的判别规则进行判断
XXGG12,,
如果如果
D2 (X,G1) D2 (X,G2 ) D2 (X,G1) D2 (X,G2 )
（4.4）
这个判别规则的等价描述为：求新样品X到G1的距离与到G2 的距离之差，如果其值为正，X属于G2；否则X属于G1。
我们考虑
D2 (X, G1) D2 (X, G2 )
(X μ1)Σ1(X μ1) (X μ2 )Σ1(X μ2 )
n1 i1
X (1) i
和
X(2)
1
n2
n2
X(2) i
i 1
Σ 的一个联合无偏估计为
Σˆ
n1
1 n2
并对测得同样p项指标（变量）数据的一个新样本，能判定这个样本归属于哪一类。
判别分析内容很丰富，方法很多。判断分析按判别的总体数来区分，有两个总体判别分析和多总体判别分析；按区分不同总体所用的数学模型来分，有线性判别和非线性判别；按判别时所处理的变量方法不同，有逐步判别和序贯判别等。判别分析可以从不同角度提出问题，因此有不同的判别准则，如马氏距离最小准则、Fisher准则、平均损失最小准则、最小平方准则、最大似然准则、最大概率准则等等，按判别准则的不同又提出多种判别方法。本章仅介绍常用的几种判别分析方法：距离判别法、Fisher判别法、Bayes判别法和逐步判别法。

判别分析解读 PPT

判别分析
Discriminant Analysis
流行病与卫生统计学系
• 聚类分析：对（样本）总体进行分类 • 判别分析：对（样本）个体进行分类
判别与聚类
• 聚类分析可以对样本/指标进行分类，判别分析只对样本进行分类。
• 聚类分析事先不知道事物的类别，也不知道应分几类；判别分析必须事先知道事物的类别，也知道应分几类。
• 在农林害虫预报中，根据以往的虫情，多种气象因子来判别一个月后的虫情是大发生，中发生或正常
• 在体育运动中，判别某游泳运动员是适合练蛙泳，仰泳还是自由泳
• 在医疗诊断中，根据某人多种检验指标来判断此人是某病患者还是非患者
判别分析－－诊断
• 临床诊断： • 急腹症的患者，需要诊断患病原因。 • 诊断阑尾炎时需要与其他急腹症作鉴别诊断；
• 聚类分析不需要分类的历史资料，能直接对样本进行分类；判别分析需要历史资料去建立判别函数，然后才能对样本进行分类。
• 判别分析：根据判别对象若干个指标的观测结果判定其应属于哪一类的统计学方法。
应用
• 在经济学中，根据人均国民收入，人均工农业产值，人均消费水平等多个指标来判定一个国家的经济发展程度所属等级
以p=q=k=2 来说明Fisher判别分析法的基本原理和计算方法
根据Fisher判别分析法的基本原理，就是要选择一组适当的系数 c 1 , c 2 ,…, c k ，使得类间差异D最大且类内差异V最小，即，使得下式的值 Q 达到最大。
根据多元函数求极值的原理和方法，使得 Q 取最大值的点是Q 的一阶偏导函数等于0的方程组的解。令上述方程组的解是：那么，Fisher判别函数估计式是：
该类。 • 适合于多类的判别分析。

判别分析完整课件

D ( y(1) y( 2) )(n1 n2 2) ( ci di )(n1 n2 2)
2 i 1 m
m为判别指标数，根据自由度查F(m,n1+n2-m-1)。
（三）确定判别临界值
确定两类的判别临界值（即两类的分界点）yc，据此对未知样本作出判断。
yc
n1 y(1) n2 y( 2 ) n1 n2
在医学科研资料中经常遇到指标变量不呈正态分布或难以满足参数判别分析的要求，特别是有些变量是分类变量，不可能服从正态分布，可以用 Logistic回归分析的方法。
实际资料中一般含有较多的指标，有些指标可能对鉴别不同的类别毫无用处，或指标间彼此相关的情况时不应该用所有的指标都参与建判别函数。所以，在建函数之前，先进行变量筛选是很有必要的，即逐步判别分析,此法建立的函数更简洁，效果也更好。此外,对于某些指标间存在彼此相关的情况时, 先对众多的指标进行聚类，从聚成的几大类中各挑选一个最有代表性的指标，用这些典型指标建立判别函数。逐步回归、判别分析、聚类分析等方法可以联合应用。
y ci xi
i 1 n
2
n1
(y
i 1
n2
i ( 2)
y( 2 ) )
2
y(1) ck xk (1)
k 1
n1
y( 2) ck xk ( 2)
k 1
n2
根据求极值的原理，求I对判别系数Ci的偏导数，使其等于零，得到下列方程组：
f11C1+f12C2+……f1mCm=d1 f21C1+f22C2+……f2mCm=d2 ……… …… …… ……… ….. fm1C1+fm2C2+……fmmCm=dm 其中， di

判别分析-实例-PPT

对光顾该商店的顾客进行n次观察。设：n1组数据为购买者（A）
n2组数据为非购买者（B）由已知变量X1，X2，将n1+n2=n组数据分成两大类；购买者（A）—— X1i (A), X2i (A) （I=1,2,…,n1)
非购买者（B）—— X1 j (B), X2 j (B) （j=1,2,…,n2)
例：样本A，舒张血压为75mmHg，血浆胆固醇为150mg%，分别代入方程后
G1=1.12364*75+0.21222*150-72.60310=43.5029
G2=0.94031*75+0.16755*150-49.34373=46.31202
由于G1小于G2，所以样本A判为正常人组（G=2）。
大家好
19
6、计算判别指标
y 1
C1
X
1
1
C2
X
1
2
C3
X
1
3
0.216928.29 0.01820 6.42 0.05604 6.00
2.251533
y 2
C1
X
2
1
C2
X
2
2
C3
X
2
3
0.21692 3.20 0.01820 3.80 0.05604 4.00
0.987464
判别指标为
大家好
35
大家好
36
大家好
37
大家好待判样品
38
大家好
39
大家好
40
大家好
41
大家好
42
大家好
43
大家好
44
大家好
45
大家好
46

《判别分析》课件

在金融领域的应用
信用评分
利用判别分析模型，通过借款人的特征和历史表现，预测其未来违约风险，为金融机构提供信贷
决策依据。
市场风险评估
判别分析用于评估金融市场风险，通过分析市场数据和变量，预测市场走势，帮助投资者做出合
理决策。
投资组合优化
利用判别分析对投资组合进行优化，通过评估不同资产的风险和回报，为投资者提供最佳资产配
对判别分析的未来展望
改进算法
针对判别分析的假设严格问题，未来研究可以尝试改进算法，放宽假设条件，使其更适用于实际数据。
结合其他技术
可以考虑将判别分析与其它机器学习算法相结合，如神经网络、支持向量机等，以提高分类性能和泛化能力。
拓展应用领域
随着大数据时代的到来，判别分析在各个领域的应用越来越广泛，未来可以进一步拓展其应用领域，解决更多实际问题。
在市场营销中，判别分析可用于市场细分，根据消费者的购买行为、偏好和需求等因素，将市场划分为不同的细分市场，帮助企业制定更加精准的市场策略。
广告投放优化
通过判别分析对广告投放效果进行评估和优化，基于历史数据和实时监测数据，分析不同广告渠道和创意的表现，提高广告投放的效率和效果。
06 判别分析的案例分析
金融领域的判别分析案例
信用风险评估
利用判别分析对银行客户进行信用风险评估，根据客户的历史表现和其他相关信息，预测其未来违约的可能性，帮助银行制定更加精准的信贷政策。
股票市场预测
通过判别分析对股票市场走势进行预测，基于历史数据和市场信息，构建预测模型，以指导投资者进行投资决策。
1. 单变量判别函数
基于单个特征的判别函数。
2. 多变量判别函数

第六章判别分析0

0.01 -0.06 -0.01 -0.14 0.06 0.05 0.06
1.5 1.37 1.37 1.42 2.23 2.31 1.84
0.71 0.4 0.34 0.44 0.56 0.2 0.38
0 0 0 0 0 0 0
0.54
0.11
2.33
0.48
0
§2 距离判别
1 (xi x j ) dij (xi x j )
d12 (x 1 )1 (x 1 ) 2.7163
2 d 2 (x 2 )1 (x 2 ) 4.155
如果假定它们有相同的协方差
d d (x ) (x ) (x ) (x )
2 2 1 1 2 1 2 2 1 1
待判点到此类的距离
0.04 0.01 x 1.5 0.71
2 d 2 (x 2 ) 1 (x 2 ) 4.998 2
如果假定它们有相同的协方差
2 4 0.07399125 0.03584580 0.03584580 0.04369786 4 6 0.17221934 0.05686315 6 8 9 9 - 0.00132211 - 0.00180881 0.17221934 - 0.00132211 6 9 0.05686315 - 0.00180881 8 9 1.19217268 0.04478862 8 0 0.04478862 0.03705156 0 5
判别函数的常数项（ 1
2
2 0.60581 9.45 35.25 8.45 0.25362 18.73596 1.83679
） 1 ( 1 2 )

第6章判别分析(王斌会)

6.3 距离判别分析
思想：根据已知分类的数据，分别计算各类的重心即各组的均值，判别准则是对任给的一次观测，若它与第i类的重心距离最近，就认为它来自第i类。 1.两总体距离判别
第1个总体G1 抽n1个样品
第2个总体G2抽 n2个样品
判别标准
D(X, G1 ) D(X, G 2 ) D(X, G1 ) D(X, G 2 ) D(X, G1 ) D(X, G 2 )
5-5
2.计算判别界值
计算各类判别值均值：
两均值中点为界点：
Y1 Y2 Y0 2
3.建立判别标准（1）当 Y1 Y2 时，Y<Y0,则X∈G1，否则X∈G2 （2）当 Y1 Y2 时，Y<Y0,则X∈G2，否则X∈G1 （3）当 Y1 Y2 时，待判
5-6
4.实例分析
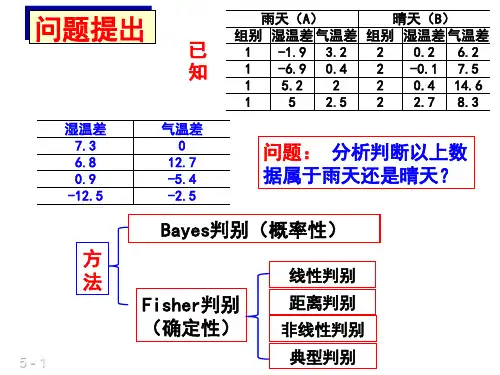
雨天（A）晴天（B）组别湿温差气温差组别湿温差气温差 1 -1.9 3.2 2 0.2 6.2 1 -6.9 0.4 2 -0.1 7.5 1 5.2 2 2 0.4 14.6 1 5 2.5 2 2.7 8.3
(tab=table(G,newG)) #混淆矩阵
newG G 1 2 1 9 1 2 1 9
sum(diag(prop.table(tab)))=0.9 #判对率 predict(ld,data.frame(x1=8.1,x2=2.0),data=d6.1) #判对率判别分析结论：明天x1=8.1，x2=2.0，预测明天是雨天，此 90%。 5次准确率为 -9
问题：现根据该资料建立判别函数，根据判别准则进行回判，假设有一新厂商推销其产品，Q=8.0,C=7.5, P=65,预测该产品销售前景如何？
5 - 12

判别分析(共27张PPT)

w11 w12 w1 p w1r
w
21
w22
w2p
w2r
Qw＝
w
p1
w p2 w pp
w
pr
wr1 wr 2 wrp wrr
使其中虚线左上部分便是只含 p 个变量的模型中的
类内离均差平方和矩阵Q( p )，而整个矩阵则是含p＋1
w
个变量的模型中的类内离均差平方和矩阵Q ( p 1) 。
第12章判别分析Discrimination Analysis
判别分析
：从反映个体性质各个侧面的P个变量出发，通过
定量分析，最终将其判归某一已知总体，从而将对个体的研究置于更为广泛的总体研究背景上。
各种判别分析都是按照某种判别原则（视判别方
法不同而不同），在e
对变量进行剔除和引进的方法差异显著地大于类内差异呢？还需进行测验。
第三节逐步判别分析方法
Stepwise Discrimination Analysis
Wilk’s Λ统计量何分类”、“某一个事例（或样品）属于那一类”等问题是并不知晓；
如果已知将原应属于Gi的样品误判为属于Gj所造成
第二节贝叶斯判别分析
|Q | |Q |w 设叶X斯，判Y别是法从的均判值别向函量数为）μ，，协按方判差别阵函为数wΣ值的的总大体小G来中抽取的两个样品，定义X，Y之间的马氏距离平方为：
＝ ──── ＝── 用 F 测验可以检验增长是否显著。
|Q ＋Q | |Q | h 第与五多步元、回如归果分有析待相判似数，据在，进将行其判代别入分，析并时判，别并e归不类是。
统计量为p，增加一个变
量 (x ) 后的 Bayes Discrimination Analysis

判别分析.ppt

注意事项
1. 判别分析效果的好坏关键是训练样本。原始分类正确，指标选择合适，测量精确，样品数多。 2. 判别类别越多，效果越差，必要时可进行多个两两判别。 3. 两分类的Fisher和Bayes判别等价：对于两类判别， Bayes准则两个分类函数之差就是Fisher判别函数。 4. 需要进行前瞻性考核，虽然回顾性考核效果很好，但它并不能说明该判别规则效果很好。这就好比全部用做过的例题来考核学生，即使得满分也不能说明该学生已很好地掌握了这门课程。
本例：训练样本：已确诊癌症的病人；无癌症的病人。
指标：X1为三倍体的得分，X2为八倍体的得分，X3为不整倍体的得分。
根据样本建立判别函数：
Y＝X1+10X2+10X3 判别准则：将某病人的X1，X2，X3的实测值，代入判别函数。
本例：判别准则为Y>100判断为癌症，
Y<100判断为非癌症。
数据要求
Original
Count
Cross-validated a Count
类别 a b c a b c
a 9 0 0 9 1 0
b 2 9 3 2 8 3
c 0 1 6 0 1 6
Total 11 10 9 11 10 9
a. Cross validation is done only for those cases in the analysis. In cross validation, each case is classified by the functions derived from all cases other than that case.
其中
SZ2
D2 (Z1 Z2 )2 / SZ2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11
22
2
xp p
22
2、按区分不同总体所用的数学模型分有线性判别和非线性判别
3、按判别准则的不同有距离判别、费歇尔（Fisher）判别和贝叶斯（Bayes）判别。
15 15
判别分析的假设前提
• 每一个判别变量不能是其他判别变量的线性组合
• 各组变量的协方差阵相等 • 各判别变量之间具有多元正态分布
16 16
第二节距离判别
• 而在判别分析中，至少有一个已经明确知道类别的“训练样本”，利用这个数据，就可以建立判别准则，并通过预测变量来为未知类别的观测值进行判别了。
6
聚类分析 7
聚类要注意的问题
• 聚类结果主要受所选择的变量影响。如果去掉一些变量，或者增加一些变量，结果会很不同。
• 相比之下，聚类方法的选择则不那么重要了。因此，聚类之前一定要目标明确。
-1
Σ2
x
-
μ
=
x
-
μ
-
Σ
1 2
Σ
-
1 2
x
-
μ
= x - μ Σ-1 x - μ
20 20
3、若变量之间是相互无关的，则协方差矩阵为对角矩阵
11
Σ
22
1
11
1
pp
Σ1
22
1
pp
21
21
此时的马氏距离为
1
11
1
d
2
(x,
G)
(x
-
μ)
22
(x - μ)
1
pp
x1 1 2 x2 2 2
• 另外就分成多少类来说，也要有道理。只要你高兴，从分层聚类的计算机结果可以得到任何可能数量的类。但是，聚类的目的是要使各类距离尽可能的远，而类中点的距离尽可能的近，而且分类结果还要有令人信服的解释。这一点就不是数学可以解决的了。
8
判别分析
9
概述距离判别法贝叶斯判别法费歇尔判别法逐步判别法
（一）马氏距离距离判别的最直观的想法是计算样品到第i类总体的平均数的距离，哪个距离最小就将它判归哪个总体，所以，我们首先考虑的是是否能够构造一个恰当的距离函数，通过样本与某类别之间距离的大小，判别其所属类别。
17
设 x (x1, x2,, xm )和 y ( y1, y2,,是ym从) 期望
13
判别分析举例：
• 根据发掘出来的人类头盖骨的高、宽等特征来判断其是男性还是女性。
• 在税务稽查中，要判断某企业是否偷漏税。 • 医生对病情的诊断。 • 信用风险的判定。 • 成功概率的判定。 • 企业运行状态或财务状况的判定。
14 14
二、判别分析的种类
1、按判别的组数分有两组判别分析和多组判别分析
4
• 聚类分析是根据事物本身的特性研究个体分类的方法，原则是同一类中的个体有较大的相似性，不同类中的个体差异很大。
• 判别分析是根据表明事物特点的变量值和它们所属的类，求出判别函数。根据判别函数对未知所属类别的事物进行分类的一种分析方法。
5
判别分析和聚类分析有什么不同呢？
• 主要不同点就是，在聚类分析中一般人们事先并不知道或一定要明确应该分成几类，完全根据数据来确定。
分类
• 俗语说，物以类聚、人以群分。
• 但什么是分类的根据呢？
• 比如，要想把中国的县分成若干类，就有很多种分类法；
• 可以按照自然条件来分，
• 比如考虑降水、土地、日照、湿度等各方面；
• 也可以考虑收入、教育水准、医疗条件、基础设施等指标；
• 既可以用某一项来分类，也可以同时考虑多项
指标来分类。
10
第一节概述
一、什么是判别分析？设有k个总体G1，G2，…，Gk，希望建立一
个准则，对给定的任意一个样本x，依据这个准则就能判断它是来自哪个总体。应当要求这种准则在某种意义下是最优的，如：错判概率最分类的训练样本
判别分析方法
判别函数
判别分析是根据观测到的某些指标对所研究的对象进行分类的一种多元统计分析方法。在医学研究中经常遇到这类问题；例如, 临床上常需根据就诊者的各项症状、体征、实验室检查、病理学检查及医学影像学资料等对其作出是否有某种疾病的诊断或对几种可能患有的疾病进行鉴别诊断，有时已初步诊断为某种疾病，还需进一步作出属该类疾病中哪一种或哪一型的判断。
1
分类学是人类认识世界的基础科学。聚类分析和判别分析是研究事物分类的基本方法，广泛地应用于自然科学、社会科学、工农业生产的各个领域。
在自然科学和社会科学的各个领域经常遇到需要对某个个体属于哪一类进行判断。如动物学家对动物如何分类的研究和某个动物属于哪一类、目、纲的判断。
2
判别
• 有一些昆虫的性别很难看出，只有通过解剖才能够判别；
• 但是雄性和雌性昆虫在若干体表度量上有些综合的差异。于是统计学家就根据已知雌雄的昆虫体表度量（这些用作度量的变量亦称为预测变量）得到一个标准，并且利用这个标准来判别其他未知性别的昆虫。
• 这样的判别虽然不能保证百分之百准确，但至少大部分判别都是对的，而且用不着杀死昆虫来进行判别了。
3
什么是判别分析
建立判别准则
未知样品判别归类
12
判别分析利用已知类别的样本培训模型，为未知样本判类的一种统计方法。
它产生于本世纪30年代。近年来，在自然科学、社会学及经济管理学科中都有广泛的应用。判别分析的特点是根据已掌握的、历史上每个类别的若干样本的数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则。然后，当遇到新的样本点时，只要根据总结出来的判别公式和判别准则，就能判别该样本点所属的类别。13
18
马氏距离和欧式距离之间的差别
马氏距离 d 2(x,G) (x - μ)Σ-1(x - μ)
欧氏距离
d 2(x,G) (x - μ)(x - μ)
19 19
马氏距离有如下的特点：
1、马氏距离不受计量单位的影响;
2、马氏距离是标准化后的变量的欧式距离
y
=
-1
Σ2
x
-
μ
yy
=
-1
Σ2
x
-
μ
μ=
(1, 2,和方, 差m )阵 Σ=
ij mm 0
的总体G抽得的两个观测值，则
X与Y之间的Mahalanobis距离
d 2 (x,y) (x y)1(x y)
样本X和Gi类之间的马氏距离定义为X与Gi类重心间的距离：
d 2 (x,Gi ) (x i )1(x i ) i 1,2,, k 18