浅析数学期望在经济生活中的应用
- 格式:pdf
- 大小:239.57 KB
- 文档页数:2

数学期望在经济决策中的应用摘要我们都知道,随着社会的发展,经济全球化的进一步深入,“经济”已经成为社会关注的热点问题,而股票,期权,投资,最佳进货量等经济学问题又与人们紧密联系,为了使人们获得最大收益,就需要我们利用专业的数学知识进行分析,决策。
而数学期望在这里发挥了重要的作用。
这篇论文主要介绍了数学期望的来源,定义,以及应用。
期望值在经济方面的大量应用,例如职位决策,风险投资,最优库存和期权定价。
这让我们更好的认识到期望的广泛应用性和重要性。
关键字:数学期望应用经济AbstractAs we all know, with the development of society and the further economical globalization ,"Economy" has become the hot issues of social concern .The economics of stocks, options, investment, best purchase amount and so on closely contact with people. In order to enable people to gain maximum benefit we need to take advantage of the professional knowledge of mathematics to analyze, decision-making. The mathematical expectation played an important role.This thesis mainly introduces the origin, the definition, and the applications of mathematical expectation, A number of applications of the expected valued in economics such as post decision, risk investment, optimal inventory and option pricing .are given rise to a better understanding of its extensive applications and significance.key words:Mathematical expectation ; Applications ; Economics.目录1.数学期望与经济决策,,,,,,,,,,,,,,,,,, 11.1 引言,,,,,,,,,,,,,,,,,,,,,,,,, 1* ■ * JI 口J J J J J J J J J J J J J J J J J J J J J J J J J * 1.2 数学期望的来源,,,,,,,,,,,,,,,,,,,,, 11.3 数学期望的定义,,,,,,,,,,,,,,,,,,,, 22. 数学期望在经济决策中的应用,,,,,,,,,,,,,,, 22.1 决策方案问题,,,,,,,,,,,,,,,,,,,, 22.2 生产与销售利润问题,,,,,,,,,,,,,,,,,,, 32.3 期权定价问题,,,,,,,,,,,,,,,,,,,,,, 53. 结果与结论,,,,,,,,,,,,,,,,,,,,,,, 64. 收获与致谢,,,,,,,,,,,,,,,,,,,,,,, 75. 参考文献,,,,,,,,,,,,,,,,,,,,,,,, 81 .数学期望与经济决策1.1引言我们知道,概率论是从数量上研究随机现象的学科,而随机变量的分布函数能够全面的描述随机变量取值的统计规律性。

浅析数学在金融经济分析中的应用论文金融业具有指标性、垄断性、高风险性、效益依赖性和高负债经营性的特点。
下面是我为你带来的浅析数学在金融经济分析中的应用论文,欢迎阅读。
【摘要】文章首先针对金融数学的概念和应用进行分析,而后进一步在此基础之上,对于确定性数学方法和不确定性数学方法的应用特征展开分析,能够帮助实现对金融领域数学学科应用状况的简要了解。
【关键词】数学;金融;经济;分析金融市场的存在与发展历史悠久,但是与其他自然学科相比,在对数学的运用方面,一直都进展缓慢。
这种滞后的进展来源于多个方面,但最为主要的方面在于,金融交易活动中存在的大量不确定因素,其中人的因素占据了大部分,诸如心理因素等,都造成了金融工作环境中的复杂特征,进一步妨碍了金融领域中数学参与的进展。
一、金融数学的概念与应用随着金融体系自身的发展,现代金融理论已经不同以往而成为一个独立学科。
与传统的金融体系相比,现代金融学开始将诸多学科包容到这一体系中来,其中不仅仅有经济学和数学,也包括了诸如心理行为学和社会学等,在重视人的心理以及行为变化的基础上,开始采用数学的方法展开对于金融学的分析。
而所有这一切,都在20世纪后期不断涌现出来,一方面,更多的适当的数学方法开始应用在金融问题的解决方案中;另一方面,这些金融问题也向数学和统计学提出了实践环境中极具价值的研究方向。
这样的推动力量,促成了金融学和数学的融合,并且逐步形成新的学科,即金融数学。
在这个新的学科领域中,现代数学工具的大量应用成为不容忽视的特征,并且进一步推动着金融与数学的融合,并且数学的相关理论与方法,为金融学的发展提供了不容置疑的支持。
从广义的角度看,金融数学是指应用数学理论和方法,研究金融经济运行规律的一门新兴学科,而从狭义而言,其主要作用于不确定条件下的证券组合选择和资产定价理论。
从应用特征和方法的角度看,金融数学通过随机控制、分析、微分、规划、统计、非线性与线性分析等方法,来处理金融环境中收益优化以及风险控制等方面的问题,并且用于处理在金融市场存在失衡特征的情况之下,实现金融风险的综合管理。
![浅谈数学期望的应用[权威资料]](https://uimg.taocdn.com/50b079ce5901020206409c65.webp)
浅谈数学期望的应用[权威资料] 浅谈数学期望的应用[摘要] 离散型随机变量数学期望是概率论和数理统计的重要概念之一,是用概率论和数理统计来反映随机变量取值分布的特征数。
通过探讨数学期望在经济和实际问题中的一些简单应用,以期让学生了解数学期望的理论知识与人类实践紧密联系,它们是不可分割、紧密联系的。
[关键词] 数学期望;离散型随机变量【】 O211.67 【】 A 【】 1007-4244(2013)07-124-2一、离散型随机变量数学期望的内涵在概率论和统计学中,离散型随机变量的一切可能的取值xi与对应的概率P(=xi)之积的和称为数学期望(设级数绝对收敛),记为E(x)。
数学期望又称期望或均值,其含义实际上是随机变量的平均值,是随机变量最基本的数学特征之一。
但期望的严格定义是?xi*pi绝对收敛,注意是绝对,也就是说这和平常理解的平均值是有区别的。
一个随机变量可以有平均值或中位数,但其期望不一定存在。
二、离散型随机变量数学期望的作用期望表示随机变量在随机试验中取值的平均值,它是概率意义下的平均值,不同于相应数值的算术平均数。
是简单算术平均的一种推广,类似加权平均。
在解决实际问题时,作为一个重要的参数,对市场预测,经济统计,风险与决策,体育比赛等领域有着重要的指导作用,为今后学习高等数学、数学分析及相关学科产生深远的影响,打下良好的基础。
作为数学基础理论中统计学上的数字特征,广泛应用于工程技术、经济社会领域。
其意义是解决实践中抽象出来的数学模型进行分析的方法,从而达到认识客观世界规律的目的,为进一步的决策分析提供准确的理论依据。
三、离散型随机变量的数学期望的求法离散型随机变量数学期望的求法常常分四个步骤:1.确定离散型随机变量可能取值;2.计算离散型随机变量每一个可能值相应的概率;3.写出分布列,并检查分布列的正确与否;4.求出期望。
四、数学期望应用(一)数学期望在经济方面的应用例1: 假设小刘用20万元进行投资,有两种投资方案,方案一:是用于购买房子进行投资;方案二:存入银行获取利息。

数学期望在实际问题中的应用探讨摘要:数学期望是概率论中的一个重要概念,是随机变量的数字特征之一,体现了随机变量总体取值的平均水平,本文主要阐述了数学期望的定义和性质,讨论了实际生活中的某些应用问题,从而使我们能够使用科学的方法对其进行量化的评价,平衡了极大化期望和极小化风险的矛盾,达到我们期望的最佳效果。
关键词:数学期望;实际问题;应用在经济生活中,有许多问题都可以直接或间接的利用数学期望来解决,风险决策中的期望值法便是处理风险决策问题常用的方法。
数学期望是随机变量的数字特征之一,它代表了随机变量总体取值的平均水平。
1 期望的概念及性质1.1 离散型随机变量的数学期望设X 是离散型随机变量,其分布律为P(X =i x )= i p (i=1,2……),若级数1i i i x p ∞=∑ 绝对收敛,则称该级数的和为X 的数学期望,记作)(X E ,即: ∑∞==1)(i i i p x X E1.2 连续型随机变量的数学期望设)(x f 为连续型随机变量X 的概率密度,若积分()xf x dx +∞-∞⎰绝对收敛,则称它为X 的数学期望,记作)(X E ,即: ⎰∞∞-=dx x xf X E )()( 1.3 期望的性质1)c c c E ,)(=为任意常数;2)c X cE cX E ),()(=为常数,X 为变量;3)Y X Y E X E Y X E ,),()()(+=+为变量;4)若Y X ,独立,则)()()(Y E X E XY E =。
2 期望的应用2.1 求职面试问题假如你得到三个有可能成为你的雇主的面试通知,每个雇主都有不同的空缺职位:一般的,好的,极好的,其工资分别为Y2500,Y3000,Y4000.你估计你得到一般的职位可能为0.4,而得到好的和极好的职位的可能性分别为0.3和0.2,有0.1的可能性使你得不到任何职位.每家公司都要求你在面试结束时表态接受或拒绝他们提供给你的职位你应遵循什么策略呢?分析:一般来说,你可以采取的每个行动方案的期望值把决策建立在第一次面试该做什么的基础上,就本问题而言要这样做是困难的,因为一种决策方案(继续去做第二次面试)会由于在第一次面试结束时我们可以做出另一个决策而有不确定的结果。

数学期望在经济生活中的应用【摘要】数学期望是随机变量的重要数字特征之一。
本文通过探讨数学期望在决策、利润、委托代理关系、彩票等方面的一些实例,阐述了数学期望在经济和实际问题中的应用。
【关键词】随机变量数学期望经济应用数学期望(mathematical expectation)简称期望.又称均值,是概率论中一项重要的数字特征.在经济管理工作中有着重要的应用。
本文通过探讨数学期望在经济和实际问题中的一些简单应用,以期起到让学生了解知识与人类实践紧密联系的丰富底蕴,切身体会到“数学的确有用”。
一.决策方案问题决策方案即将数学期望最大的方案作为最佳方案加以决策。
它帮助人们在复杂的情况下从可能采取的方案中做出选择和决定。
具体做法为:如果知道任一方案A(i=1,2,⋯,m)在每个影响因素S(j=1.2,⋯,n)发生的情况下,实施某种方案所产生的盈利值及各影响因素发生的概率,则可以比较各个方案的期望盈利,从而选择其中期望盈利最高的为最佳方案。
1.风险方案假设某公司预计市场的需求将会增长。
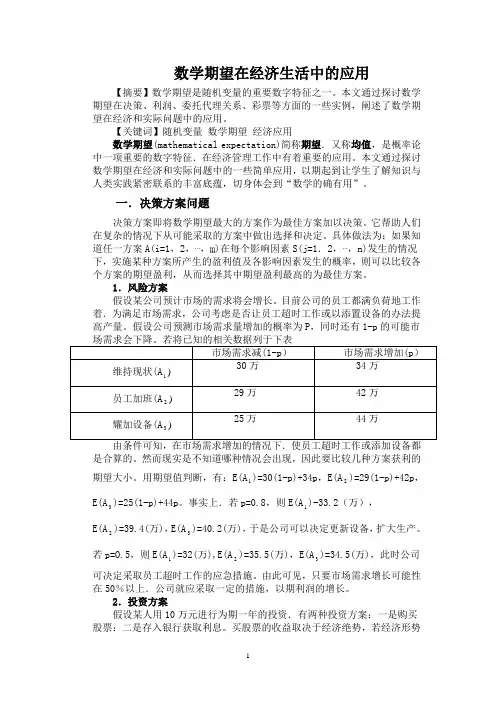
目前公司的员工都满负荷地工作着.为满足市场需求,公司考虑是否让员工超时工作或以添置设备的办法提高产量。
假设公司预测市场需求量增加的概率为P,同时还有1-p的可能市是合算的。
然而现实是不知道哪种情况会出现,因此要比较几种方案获利的期望大小。
用期望值判断,有:E(A1)=30(1-p)+34p,E(A2)=29(1-p)+42p,E(A3)=25(1-p)+44p。
事实上.若p=0.8,则E(A1)-33.2(万),E(A2)=39.4(万),E(A3)=40.2(万),于是公司可以决定更新设备,扩大生产。
若p=O.5,则E(A1)=32(万),E(A2)=35.5(万),E(A3)=34.5(万),此时公司可决定采取员工超时工作的应急措施。
由此可见,只要市场需求增长可能性在50%以上.公司就应采取一定的措施,以期利润的增长。
2.投资方案假设某人用10万元进行为期一年的投资.有两种投资方案:一是购买股票:二是存入银行获取利息。


数学期望在经济决策中的应用研究作者:张茜茹来源:《今日财富》2020年第06期在开展各项经济决策时,不仅需要考慮各项工作的经济效益,还应保证各项数学模式在经济决策中的应用力度,强化经济决策水平,落实我国现有社会经济发展的目标。
当前各行业在开展经济决策时,还会在其中应用数学期望,不断提高经济决策水平,避免经济决策受到外在因素的影响。
本文首先简要概述数学期望,之后阐述数学期望在经济决策中的应用,以彰显经济决策的现实内涵。
一、引言在开展各项经济决策时,不仅需要考虑各项经济内涵在经济决策中的现实作用,还应借助数学期望对经济决策实施优化处理,改善经济决策过程中出现的问题,确保经济决策与我国现有社会经济发展要求相契合。
与此同时,还应保证经济管理人员对数学期望有所了解,促使相关人员灵活应用数学期望开展经济决策,使得有关部门在开展经济决策时出现问题的几率降到最低。
二、数学期望的概述在对数学期望进行研究中,了解到数学期望是指试验中每次可能结果的概率乘以其结果的总和。
该项数学特征不仅能够将概率学和统计学中各项数据信息表达出来,还能将随机变量中平均取值的大小全面反映出来,以避免企业在后期开展经济决策以及其他业务工作时出现问题。
而且在应用数学期望时,还应保证期望值的合理性,避免企业在应用数学期望开展经济决策时出现问题,确保经济决策能够满足企业良性发展要求。
而且数学期望主要包括离散型和连续型两种类型,这就应针对数学期望的具体表现以及其他方面因素分析这两种类型的差异和共同点,不断优化数学期望,以满足经济决策的现实要求。
三、数学期望在经济决策中的应用一般来说,企业在开展经济决策时经常会受到外在因素的干扰,如果不能及时改善企业在开展经济决策时出现的问题,必然导致企业经济效益和现实发展水平下降,这对于企业综合发展也有很大的影响。
基于此,必须强化数学期望在经济决策中的应用,不断调整企业在开展各项经济决策时出现的问题,以此满足企业良性发展要求。

[摘要]数学期望又称均值,是概率论中的一个重要概念。
随着社会经济的迅速发展,竞争越来越明显,企业所面临的经济问题也越来越多,许多实际经济问题可以通过数学期望的应用来解决。
对经济问题决策的作用进一步分析,提出数学期望可以提高经济问题解决的效率,促进经济问题解决的科学性,解析了数学期望在经济生活若干问题中的运用。
[关键词]随机变量;数学期望;经济问题;利润最大[中图分类号]O211.67[文献标志码]A[文章编号]2096-0603(2021)39-0154-02浅谈数学期望在经济问题中的应用傅桂清(福建经贸学校,福建泉州362000)一、数学期望数学期望又称均值,是概率论中的一个概念。
数学期望通过研究随机变量取值反映出的平均水平,对事物的数量关系进行分析来掌握事物的变化规律。
随着社会经济的迅速发展,竞争越来越明显,企业所面临的经济问题也越来越多。
为了能够在这残酷的竞争中屹立不倒,并能同时获取较高收益,企业就必须降低风险,降低成本,减少损失,那么决策者们就需要采用科学的方法来做出正确的经济决策,解决经济问题。
但是现实的经济社会除了受到外部因素和决策者们主观因素的影响外,还包含很多不确定性因素的影响。
所以,就需要通过数学期望来综合分析这些因素,从中选取较为合理的解决方案。
二、数学期望在经济问题决策中的作用(一)数学期望对提高经济问题解决的效率有促进作用企业决策者在企业运营的过程中将会面对很多复杂的问题,需要决策者对企业的经营情况和在行业所处的情况进行了解和把握,这不仅需要耗费大量的时间,还需要管理者投入较多的精力去思考和判断,这就使在一些决策确定后已经耽误了市场先机,使企业陷入被动。
那么企业在面临决策的时候就可以将数学期望的计算方法应用到里面,同时借助计算机的辅助工具快速地得到有效的结果,进而有利于企业管理者确定方案,极大地提高了决策的效率。
(二)数学期望为经济问题解决的科学性提供理论依据知识来源于生活,是人们在生活中科学认识事物规律的总结。

经济决策中数学期望的应用纵观几乎所有领域的发展,都能够发现数学在其中所起到的重要促进与推动作用,尤其是改革开放以来,数学在我国社会经济的发展过程中更是发挥出了至关重要的作用。
[1]比如在现代社会的经济活动中,人们要想确保所作出的经济决策是科学的、合理的,那么就必须借助数学期望来实现这一目的。
1数学期望在经济决策中的作用数学期望在经济决策中的作用主要体现在以下几个方面:首先,数学期望是经济决策中的一项重要工具。
企业在面对一些情况较为复杂的时候,往往需要企业管理者通过对大量数据的分析,然后才能作出相关经济决策,而分析这些数据常常就需要用到数学期望这一工具。
其次,数学期望可以帮助企业尽快作出相关经济决策。
在进行相关经济决策的时候,企业管理者往往需要分析大量的数据,如果不借助数学期望来快速得出结果,那么不仅会导致企业管理者在决策过程中浪费过多时间和精力,还容易使得当最终作出决策以后已经耽误了市场先机,从而使得企业因此而陷入被动局面。
[2]最后,数学期望能够确保经济决策的科学性。
在现实生活中,不少企业管理者在进行相关经济决策的时候,更多是建立在感性思考和分析这一基础上的,从而使得所作出的经济决策在实际执行过程中常常出现不合理的情况,这无疑就是决策失误了,不仅会对企业的正常运营产生影响,甚至可能使企业因此而蒙受重大的损失。
但是如果企业管理者能够运用数学期望来分析相关数据,使得所作出的经济决策是建立在数据分析结果基础之上的,相信必定能够一定程度使得经济决策的科学性得到大大增强。
[3]2数学期望在经济决策中的具体应用分析2.1在投资决策中的应用例:张某手中有20万元闲钱所以想进行一次为期一年的短期投资,目前其面临着两种投资方案,一时难以抉择选择何种方案最佳。
方案一:将20万元钱直接存进银行,拿一年这20万元钱的银行利息。
方案二:将这20万元钱全部用于购买股票。
如果选择方案一,虽然这种投资方案最保险,但是明显收益并不高,按8%的年利率算能够收益1.6万元,受货币贬值影响,甚至可能出现收益负增长的情况。

数学期望在经济决策中的应用文章通过实例介绍了数学期望在减少工作量、选择最优存储量、选择最佳进货量、总利润最大问题等方面的应用,说明了数学期望在经济决策中的重要作用.标签:数学期望经济决策应用概率论是从数量上研究随机现象统计规律性的学科,而随机变量的分布函数能够全面地反映随机变量的统计规律性.但在诸多的经济管理或决策工作中,一方面由于求出随机变量的分布函数并非易事,而且对于某些实际问题来说,并不需要对随机变量进行全面的描写,只需知道能够反映随机变量的某些重要的数字特征即可.数学期望是反映随机变量总体取值的平均水平的一个重要的数字特征,它在经济决策工作中有着广泛的应用,为决策者做出最优决策提供重要的理论依据。
一、数学期望的概念定义1(1)设离散型随机变量X的概率分布为P{X=xk}=pk,k=1,2,…,若级数绝对收敛,则称级数为离散型随机变量X的数学期望(或均值),记为EX,即。
若级数发散,则称随机变量X的数学期望不存在;(2)设连续型机变量X的概率密度函数为f(x),若积分绝对收敛,则称其为连续型随机变量X的数学期望或均值,记为E(X),定义2设Y为随机变量X的函数:Y=g(X)(g是连续函数),(1)X是离散型随机变量,分布律为P{X=xk}=pk,k=1,2,…,若级数绝对收敛,则有(2)X是连续型随机变量,概率密度函数为f(x),若积分绝对收敛,则有二、数学期望的应用1.期望值问题例1一商场共有16层楼,设有10位顾客在一层进入电梯,每位乘客在楼上任何一层出电梯是等可能的,且各乘客是否出电梯相互独立,求直到电梯中的乘客出空为止电梯需停次数X的期望值。
解:引入计数随机变量则有X=X2+X3+ (X16)由题意,每一个人在任何一层出电梯的概率为1/15,若10个人同时不在第i 层出电梯,那么电梯在该层就不停,而此时的概率为因此,进而2.减少工作量例2某商场对员工(N人)进行体检,其中普查某种疾病需要逐个验血,一般来说,若血样呈阳性,则有此种疾病;呈阴性则无此疾病.逐个验血需要N次,若N很大,验血的工作量也很大.为了能减少验血的工作量,有人提出想法:把k(k>1)个人的血样混合后再检验,若呈阴性,则k个人都无此疾病,这时k个人只需作一次检验;若呈阳性,则对k个人再分别检验,这时为弄清谁有此种疾病共需检验k+1次.若该商场员工中患此疾病的概率为p,且各人得此病相互独立,那么此种方法能否减少验血次数?若能减少,那么能减少多少工作量?解:令X表示该商场每人需要验血的次数,那么X是只取2个值的随机变量,其分布律为则每人平均验血次数为而新的验血方法比逐个验血方法平均能减少验血次数为1-EX=只要EX<1,就能减少验血的工作量。
数学期望在现实生活中的应用发布时间:2021-03-29T15:28:18.083Z 来源:《中国教工》2020年32期作者:杨付贵[导读] 在我们的日常生活中有许多随机现象和规律,需要用概率统计的方法对其进行研究。
杨付贵广州工商学院基础教学部广东佛山三水 528138摘要:在我们的日常生活中有许多随机现象和规律,需要用概率统计的方法对其进行研究。
由于数学期望是判断变量规律的基本依据之一,是概率论与数理统计课程中一个非常重要的数字特征,在我们生活中起到了至关重要的作用。
本文通过一些现实生活中的实际例子,简介数学期望在我们现实生活中的具体应用。
关键词:数学期望;概率统计;应用所谓数学期望就是随机变量的平均值,简称为均值。
它是在研究现实生活中各种随机现象和统计规律中,经常会用到的重要一个因素。
下面通过现实生活中的一些具体实例,阐述数学期望在实际经济生活中的作用和数学期望的价值意义。
1.在商店进货问题中的应用随着我国经济的不断增长,各个生产企业的管理者以及商品销售商店的经营者一直都在追求利润的最大化,为此,生产企业的管理者和商品销售商店的经营者,对下一个阶段商品的需求和供应量,往往需要进行科学的预测和估计,然后,根据所预测的数目计划最佳的生产量和策划合适的销售方案。
因此,经验丰富的生产企业的管理者以及商品销售商店的经营者,都会根据以往统计的数据,利用微积分和概率论的相关知识,求出不同商品的销售量和生产量的利润数学期望值,利用不同商品的利润的期望值来生产销售各种商品。
以期达到利润的最大化。
例1.设某种商品的每月需求量是服从[10,30]上均匀分布的随机变量,而经销商店的进货数量为区间[10,30]上的某一整数,假设该商店每销售该商品一单位可获利500元;若供大于求则处理,每处理一单位该商品亏损100元;若供不应求,则可从外部调剂供应,此时每一单位该商品仅获利300元。
为使商店所获利润的数学期望不小于9280元,试确定最小进货量。
本科毕业论文(设计)题目:数学期望在经济生活中的应用学生:学号:学院:数学与计算科学学院专业:数学与应用数学入学时间: 2009 年 9 月 5 日指导教师:职称:完成日期: 2013 年 4 月 15 日数学期望在经济生活中的应用摘要:数学期望是概率论的重要组成部分,在经济生活中常被作为一种统计指标,帮助人们做出正确的决策。
本文通过对数学期望的基本理论知识进行系统总结,重点探讨数学期望在风险决策问题、商家投资产品效益问题、买彩票问题、面试求职问题、减少工作量等问题中的应用,说明其在经济生活中具有重要的应用价值。
关键词:数学期望,随机变量,经济生活Application of mathematical expectation in the economic lifeAbstract: Mathematical expectation is an important part of probability theory, as a kind of statistical indicators in economic life to help people make the right decisions. Based on mathematical expectation systematically summarizes the basic theory of knowledge, the paper mainly discusses the mathematical expectation in any risk decision problem, merchants investment product efficiency problem, buy a lottery ticket, the job interview questions, reduce the workload and other issues, the application of it have important application value in economic life.Key words:Mathematical expectation ,random variable,economic life目录1、引言(绪论) (3)2、概率论中的数学期望 (3)2.1、数学期望的概念 (3)2.2、离散型随机变量的数学期望 (4)2.3、连续型随机变量的数学期望 (4)3、数学期望在经济生活中的应用 (5)3.1、决策方案的问题 (5)3.2、生产和销售利润的问题 (7)3.3、委托-代理的问题 (8)3.4、彩票的问题 (9)3.5、减少工作量的问题 (10)3.6、赌徒困惑和凯利准则 (11)4、结束语 (12)参考文献 (12)致谢 (12)1 引言数学期望在中学阶段就开始学习,是因为它在生活中经常用到。
感悟数学期望在实际生活中的应用离散型随机变量的期望是离散型随机变量的重要的数字特征,它从整体上描述随机变量,反映了随机变量取值的平均水平,在实际生活中有着广泛的应用。
以下几例,供参考:例1据统计一个家庭中万元以上的财产被盗的概率是,保险公司开办一年期万元以上家庭财产保险,参加者需交保险费100元,若在一年以内万元以上财产被盗,保险公司赔偿a元(100a>)。
问a如何确定,可使保险公司有望获利分析:要使保险公司获利,即()0E X>,从而将问题转化为利用不等式求a的取值范围。
解析:设X表示保险公司在参加保险人身上的收益,则X的可能取值是100,100a-,P X==;(100)0.99P X a=-=。
(100)0.01E X a=⨯+-⨯1000.010()1000.99(100)0.01=->,a∴10000a<,又∵100<<,即当a在100至10000之间取a>,∴10010000a值时保险公司可望获利。
评注:该例与生活密切相关,由此可深切体会到数学期望的应用价值。
例2某渔船要对下月是否出海做出决策,如果出海后遇到好天气,可收益6000元,如果出海后天气变坏,将损失8000元,若不出海,无论天气如何都将承担1000元损失费。
据气象部门预测,下月好天气的概率是,天气变坏的概率是,请你为该船做出决定,是出海还是不出海分析:船是出海还是不出海,关键是要看船出海的收益平均值与不出海的收益平均值1000-的大小。
解析:设该船一次出海的收益为随机变量X,则其分布列为:∴()60000.6(8000)0.4400E X=⨯+-⨯=。
∵()4001000E X=>-,∴应该选择出海。
评注:“出海”还是“不出海”,是将实际问题转到数学中来,即用数字来说明问题,数学期望反映了随机变量取值的平均水平,用它来刻画、比较措施取值的平均情况,在一些实际问题中有重要的价值。
浅析数学期望在实际生活中的应用摘要:本文主要讨论了实际生活中的某些应用问题,从而使我们能够使用科学的方法对其进行量化的评价,平衡了极大化期望和极小化风险的矛盾,达到我们期望的最佳效果。
关键词:数学期望生活应用早在17世纪,有一个赌徒向当时的法国数学家提出一个使他苦恼了很久的问题:“两个赌徒相约赌若干局,比赛规则是先胜三局者为赢家,赢家可以获得100法郎的奖励。
他们两人获胜的机率相等。
但是当其中一个人赢了2局,另一个人赢了1局的时候,由于某种原因终止了赌博。
问:赌资应该怎样分才合理?”那么如何分配这100法郎才比较公平?用概率统计的知识,不难得知,甲获胜的概率为1/2+(1/2)*(1/2)=3/4,或者分析乙获胜的概率为(1/2)*(1/2)=1/4。
因此由此引出了甲的期望所得值为100*3/4=75法郎,乙的期望所得值为25法郎。
这个故事里出现了“期望”这个词,数学期望由此而来。
在经济生活中,有许多问题都可以直接或间接的利用数学期望来解决,风险决策中的期望值法便是处理风险决策问题常用的方法。
数学期望是随机变量的数字特征之一,它代表了随机变量总体取值的平均水平。
本文主要讨论了实际生活中的某些应用问题,从而使我们能够使用科学的方法对其进行量化的评价,平衡了极大化期望和极小化风险的矛盾,达到我们期望的最佳效果。
一、资金投资问题某投资者有10万元,现有两种投资方案:一是购买股票,二是存入银行获取利息。
买股票的收益主要取决于经济形势,假设可分三种状态:形势好、形势中等、形势不好(即经济衰退)。
若形势好可获利40000元;若形势中等可获利10000元;若形势不好要损失20000元。
如果是存入银行,假设年利率为8%,即可得利息8000元。
又设年经济形势好、中等、不好的概率分别为30%、50%和20%。
试问该投资者应选择哪一种投资方案?分析:购买股票的收益与经济形势有关,存入银行的收益与经济形势无关。
因此,要确定选择哪一种方案,就必须通过计算这两种投资方案对应的收益期望值E来进行判断。