- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Heisenberg不等式表明窗口Fourier变换的时 窗半径和频窗半径, 一个减小必然引起另一个的 增大, 不能同时减小.
窗口Fourier变换的窗函数选定以后, 其时-频 窗就固定不变了, 这样就限制了窗口Fourier变换 的实际应用. 为了提取高频分量的信息, 时窗应该 尽量地窄, 而允许频窗适当地宽; 对于低频分量, 时窗则应适当加宽, 以保证至少能包含一个周期的 过程, 频窗应当尽量缩小, 保证有较高的频率分辨率.
§4.2 窗口Fourier变换简介
窗口Fourier变换是在 Fourier 变换的框架内, 将非平稳过程看成是一系列短时平稳信号的叠加, 通过在时域上加上窗口来实现短时性. 通常选择在 有限区间外恒等于零或迅速趋于零的钟形函数g(t) 作为窗函数, 用平移滑动的窗函数g(t-t)与信号f (t) 相乘, 有效地抑制了t=t 邻域以外的信号, 在t 附近 开窗, 通过平移来覆盖整个时间域. 再进行Fourier 变换, 所得的结果反映了t=t 时刻附近的频谱信息, 从而产生了时域局部化的作用.
设 f , g Lk12, k(2R是)任,意常数, 则
W (k1 f k2g) (a,b) k1 W f (a,b) k2 W g (a,b).
(2) 平移性质
设 f L2则(R),
W f (t t0 ) (a,b) W f (t) (a,b t0).
(3) 尺度法则
第四章 小波变换基础
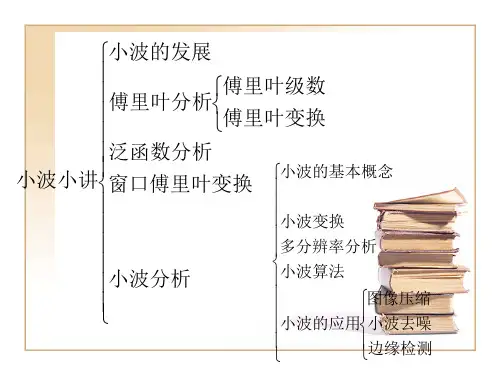
§4.1 小波变换的背景 §4.2 窗口Fourier变换简介 §4.3 连续小波变换 §4.4 二进小波变换和离散小波变换 §4.5 多分辨分析 §4.6 Mallat分解与重构算法
主要内容
小波分析是当前数学中一个迅速发展的 新领域,它也是一种积分变换,是一个时间和 频率的局域变换,因而能有效地从信号中提 取信息,通过伸缩和平移等运算功能对函数 或信号进行多尺度细化分析,解决了Fourier 变换不能解决的许多困难问题.本章简单介绍 小波变换的基本理论和应用.
2
d
-
+ G( ) 2 d
-
是频窗中心, 称
1
+
(
-
* )2
G( )
2
d
2
+ G( ) 2 d
-
是频窗半径.
当频窗函数是
时G,(类似地可)以推导出
相应的频窗中心和频窗半径为
* * , .
因此频窗中心在平移, 频窗半径不变.
在时-频坐标系中, 时窗 和频窗共同作用形成时-频 窗, 右图是通过时-频窗进行 时-频局部化的几何直观描述.
2
-
为时窗半径.
于是时窗函数g(t)的窗口为
窗[t口* t,t* t],
的宽度为2t. 下面讨论时窗函数g(t-)的时窗中心
t*
和时窗半径
t .
t*
+
t
g(t
) 2 dt
-
+
(u
)
g(u)
2
du
-
+ u g(u) 2 du + g(u) 2 du t* ,
-
-
1
t
也是由频谱 在整fˆ (个频)域
上的贡献
决定的. 所以在时域中Fourier变换没有任何分辨能
力, 通过有限频段上的 不能获得fˆ信(号f)(t)在任何
有限时间间隔内的频率信息. 因为一个信号在某个时
刻的一个小的邻域中发生了变化, 那么整个频域都要
受到影响. 这就是说, Fourier变换在时域没有局域特 性. 同样地分析可见, 在频域上Fourier变换也没有局 域特性.
间平移的作用, 而a在连续小波变换中是一个尺度 参数, 它既能改变窗口的大小与形状, 同时也能改
变连续小波的频谱结构.
常用的基本小波:
Haar小波
1,
(t) 1,
0,
0 t 1/2 1/2 t 1
其他
Morlet小波
(t
)
e
t2 2
e i0t
,
t ,
0 5.
墨西哥草帽小波(Marr小波)
窗口Fourier变换把时域上的信号f (t)映射到
时-频域平面 中(的一,个)二维函数
G f (, ).
一个常用的窗口函数是Gauss函数
g(t)
b
t2
e 4a (a,b 0),
2 a
其中a, b使得
+ g(t ) 2 dt 1. -
易见时窗中心
t* +并t 且g时(t窗) 2半d径t 0, -
(t) 1 t2
1
t2
e 2 , t .
2
定义4.5 设 为由基a本, 小b 波
续小波. 对 f 称 L2(R),
生成的连
(t)
W f
(a,b)
f , a,b
1 a
f
(t )
t
a
b
dt
为f (t)的连续小波变换.
连续小波变换具有如下一些主要性质.
(1) 线性性质
的对称性, 使得信号的重构很容易进行. 特别是后来
离散Fourier变换(DFT)的发展, 以及 1965 年提出的
快速Fourier变换(FFT)与计算机技术相结合, 使
得Fourier变换的应用更加广泛和有效, 在科学技
术的各个领域发挥过重要作用.
但是Fourier变换仅适用于确定性的平稳信号.
小波变换克服了Fourier变换和窗口Fourier变 换的缺点, 在时域和频域同时具有良好的局域化性 质, 被誉为“数学显微镜”.
1987年, 法国数学家Mallat与Meyer合作, 将计 算机视觉领域内的多尺度分析的思想引入到小波分 析中,提出了多分辨分析的概念, 统一了在此之前的 所有具体正交小波基的构造, 并且提出相应的分解 与重构快速算法. 随后Mallat将多分辨分析用于图 象处理, 取得了巨大成功.
+ g(t ) 2 dt 1. -
根据Fourier变换的反演公式, 有
f (t)g(t ) 1
2
G
f
(
,
)e i t d
,
于是
f (t) g(t )2 1
2
G
f
(
,
)e
i
t
g(
t
)d
,
从而
f (t) + g(t )2 d -
1
2
+
d
-
G
f
(
,
)e i t
g(t
)d
定义4.1 设函数
g L1(R) L2(R), tg L2(R),
则称 f (t )g的(Ftourier)变换
f (t )g(t )eitdt
为f (t)的窗口Fourier变换, 也称f (t)的Gabor变换, 记
为 G f (其,中)g,(t)称为时窗函数.
以下总是取时窗函数g(t)满足
设 f L2则(R),
W f (t) (a,b)
小波变换是泛函分析、调和分析和数值分析 等数学分支发展的综合结晶,作为一种数学理论 和方法在科学技术领域引起了越来越多的关注和 重视. 小波分析的应用是与小波分析的理论研究 紧密地结合在一起的. 对于处理性质随时间稳定不 变的信号, 理想工具仍然是Fourier分析. 但是在实 际应用中的绝大多数信号是非稳定的, 而特别适用 于非稳定信号的工具就是小波分析. 小波分析的应 用领域十分广泛,包括信号分析和图象处理、语音 识别与合成、医学成像与诊断等方面.
在1910年Haar提出的规范正交基应该是小波分 析的最早萌芽. 1938年, Littlewood-Paley 对 Fourier 级数按二进制频率成分进行分组. 1965年, Galderon 发现再生公式, 它的离散形式已接近小波展开. 1981 年,Stormberg对Haar系进行了改进, 证明了小波函 数的存在性.小波概念的真正出现应该是在1984年, 当时法国地球物理学家Morlet在分析地震数据时提 出将地震波按一个确定函数的伸缩平移系展开. 然 后数学家Meyer对Morlet提出的方法进行系统研究, 并与其他一些人的工作联合奠定了小波分析的基础.
从定义可以看出, 为了应用Fourier变换去研究一个
信号的频谱特性, 必须获得在整个时域
中信号的全部信息. 由于
即Fouerieri变t换 1,
的积分核在任何情形下的模都是1, 所以信号f (t)的
频谱 fˆ的(任一) 频点值都是由 f (t) 在整个时间域
t
上的贡献决定的; 反之, 信号f (t)在任一时刻的状态
f , g L2(R),
表示空间 中L2的(内R积) , 是 的共轭g(. t ) g(t )
§4.1 小波变换的背景
自从1822年Fourier发表《热传导解析理论》 以来,Fourier变换一直是在信号处理等工程应用 领域中得到广泛使用且极其有效的一种分析手段.
Fourier变换和逆变换将研究的内容从时域变换到 频域, 也就是从一个空间变换到另一个空间, 这种 研究思想和方法是重大的创新.
为研究信号在局部时间范围的频域特征, 1946 年Gabor提出了著名的Gabor变换, 之后又进一步发 展为窗口Fourier变换, 也称短时Fourier变换(STFT). STFT弥补了Fourier变换的一些不足, 已在许多领域 获得了广泛的应用. 但是, 由于STFT的时-频窗口大 小和形状固定, 与时间和频率无关,所以并没有很好 地解决时-频局部化问题, 这对于分析时变信号来说 是不利的. 高频信号一般持续时间很短, 而低频信号 持续时间较长, 因此, 我们期望对于高频信号采用小 时间窗, 对于低频信号则采用大时间窗进行分析.