【小学数学】小升初数学找规律练习题目
- 格式:pdf
- 大小:259.63 KB
- 文档页数:7

第一部分:重点中学招生考试题1.(西城实验考题)有一批长度分别为1,2,3,4, 5,6,7,8,9,10和11厘米的细木条,它们的数量都足够多,从中适当选取3根木条作为三条边,可围成一个三角形;如果规定底边是11厘米,你能围成多少个不同的三角形?【解】由于数量足够多,所以考虑重复情况;现在底边是11,我们要保证的是两边之和大于第三边,这样我们要取出的数字和大于11.情况如下:一边长度取11,另一边可能取1~11总共11种情况;一边长度取10,另一边可能取2~10总共9种情况;…一边长度取6,另一边只能取6总共1种;下面边长比6小的情况都和前面的重复,所以总共有1+3+5+7+9+11=36种。
2.(三帆中学考题)有7双白手套,8双黑手套,9双红手套放在一只袋子里。
一位小朋友在黑暗中从袋中摸取手套,每次摸一只,但无法看清颜色,为了确保能摸到至少6双手套,他最少要摸出手套()只。
(手套不分左、右手,任意二只可成一双)。
【解】考虑运气最背情况,这样我们只能是取了前面5双颜色相同的后再取三只颜色不同的,如果再取一只,那么这只的颜色必和刚才三只中的一只颜色相同故我们至少要取5×2+3+1=14只。
3.(人大附中考题)某次中外公司谈判会议开始10分钟听到挂钟打钟(只有整点时打钟,几点钟就响几下),整个会议当中共听到14下钟声,会议结束时,时针和分针恰好成90度角,求会议开始的时间结束的时间及各是什么时刻。
【解】因为几点钟响几下,所以14=2+3+4+5,所以响的是2、3、4、5点,那么开始后10分钟才响就是说开始时间为1点50分。
结束时,时针和分针恰好成90度角,所以可以理解为5点过几分钟时针和分针成90度角,这样我们算出答案为10÷11/12=1010/11分钟,所以结束时间是5点1010/11分钟。
(可以考虑还有一种情况,即分针超过时针成90度角,时间就是40÷11/12)4.(101中学考题)4道单项选择题,每题都有A、B、C、D四个选项,其中每题只有一个选项是正确的,有800名学生做这四道题,至少有_________人的答题结果是完全一样的?【解】因为每个题有4种可能的答案,所以4道题共有4×4×4×4=256种不同的答案,由抽屉原理知至少有: [799/256]+1=4人的答题结果是完全一样的.5.(三帆中学考题)设有十个人各拿着一只提桶同时到水龙头前打水,设水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,如此下去,当只有两个水龙头时,巧妙安排这十个人打水,使他们总的费时时间最少,这时间等于_________分钟.【解】不难得知应先安排所需时间较短的人打水.不妨假设为:第一个水龙头第二个水龙头第一个 A F第二个 B G第三个 C H第四个 D I第五个 E J显然计算总时间时,A、F计算了5次,B、G计算了4次,C、H计算了3次,D、I计算了2次,E、J计算了1次.那么A、F为1、2,B、G为3、4,C、H为5、6,D、I为7、8,E、J为9、10.所以有最短时间为(1+2)×5+(3+4)×4+(5+6)×3+(7+8)×2+(9+10)×1=125分钟.评注:下面给出一排队方式:第一个水龙头第二个水龙头第一个 1 2第二个 3 4第三个 5 6第四个 7 8第五个 9 106.(八中考题)甲、乙两厂生产同一规格的上衣和裤子,甲厂每月用16天生产上衣,14天做裤子,共生产448套衣服(每套上衣、裤子各一件);乙厂每月用12天生产上衣,18天生产裤子,共生产720套衣服。

(小升初奥数拓展)小学数学找规律专项复习试题大全(有答案解析)专项练习考试范围:;考试时间:100分钟;命题人:xxx注意事项.1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题(题型注释)1、明明用石子摆出了图中的图案,根据规律判断第6个图案中石子总数为( )。
A.12B.16C.20D.242、为了把2008年北京奥运会办成绿色奥运,全国各地都在加强环保,植树造林。
某单位计划在通往两个比赛场馆的两条路的(不相交)两旁栽上树,现运回一批树苗,已知一条路的长度是另一条路长度的两倍还多6000米,若每隔4米栽一棵,则少2754棵;若每隔5米栽一棵,则多396棵,则共有树苗多少棵?()A.8500棵B.12500棵C.12596棵D.13000棵二、填空题(题型注释)3、有这样一组数:1,2,3, 5,…现以这组数据的数作为正方形边长的长度构造如下正方形;再分别从左到右取2个、3个、4个、5个正方形拼成如下长方形记为:①②③④(如下图)。
则第⑨个长方形的周长是()。
4、先画出第五个图形并填空。
再想一想:后面的第10个方框里有()个点,第51个方框里有()个点。
5、用小棒按照如下方式摆图形:(1)摆第5个图形需用( )根小棒。
(2)摆第n个图形需用( )根小棒。
6、1=12,1+3=22,1+3+5=32,1+3+5+7=( )2,…,1+3+5+7+9+11+13+15=( )2。
根据上面的结论算一算:1+3+5+7+9+5+3+1=( );1+3+5+7+9+11+13=( )。
7、先画出第五个图形并填空。
再想一想,第10个方框里有( )个点,第51个方框里有( )个点。
8、如图,当n=1时,图中有1个圆;当n=2时,图中有7个圆;当n=3时,图中有19个圆;…,按此规律,当n=5时,图中有个圆.9、观察图中的三角形数阵,则第50行的最后一个数是______.10、找规律填数.6,7,10,15,22,3,15,35,63,99,,195.11、用小棒摆出右面的图形.摆第1个图形要4根小棒.那么摆第5个图形要( )根小棒,摆第n个图形要( )根小棒。
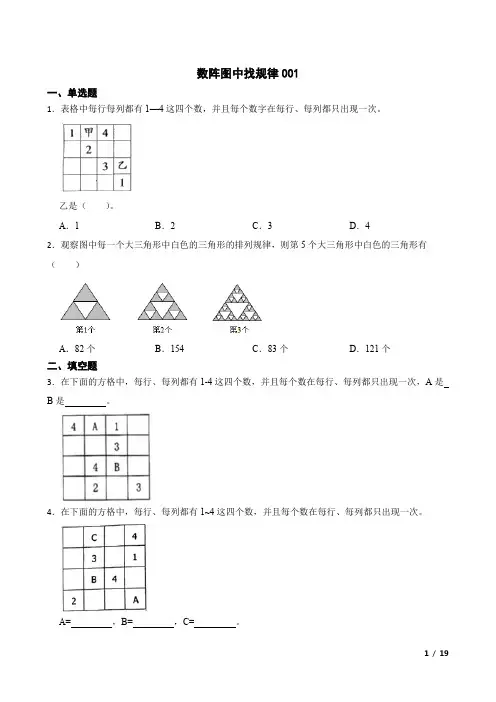
数阵图中找规律001一、单选题1.表格中每行每列都有1—4这四个数,并且每个数字在每行、每列都只出现一次。
乙是()。
A.1B.2C.3D.42.观察图中每一个大三角形中白色的三角形的排列规律,则第5个大三角形中白色的三角形有()A.82个B.154C.83个D.121个二、填空题3.在下面的方格中,每行、每列都有1-4这四个数,并且每个数在每行、每列都只出现一次,A是B是。
4.在下面的方格中,每行、每列都有1~4这四个数,并且每个数在每行、每列都只出现一次。
A=,B=,C=。
5.下面的方格中,每行、每列都有1-4这4个数字,并且每个数字在每行、每列都只出现一次,那么A是,B是,C是。
6.把3,4,5填入方格中,每一横行,每一竖行的数字不能重复,A=。
7.下面一张数表里数的排列存在着某种规律,请你找出规律之后,按照规律填空。
8.欢欢在钉子板上围了一个多边形,这个多边形边上的钉子数为13,内部钉子数为4,则这个多边形的面积数为。
9.在下面的方格中,每行、每列都有1~4这四个数字,并且每个数字在每行、每列都只出现一次。
那么A是,B是,C是。
10.在下面的方格中,每行、每列都有1-4这四个数,并且每个数在每行、每列都出现一次。
A应该是。
11.观察表一,寻找规律。
表二、表三分别是从表一中截取的一部分。
其中,a=,b=。
12.观察下列各数组成的三角形,根据各数阵的排列规律,写出第五行的数(从左到右填写)13.如图,10在第一行第2个。
19在第2行第4个。
12在第行第个。
按照这样的排列规律,47在第行第个。
14.观察下列点阵,在里画出第六个点阵,并写出它的算式。
15.在下边的方格中,每行、每列都有1~4这四个数,并且每个数在每行、每列都只出现一次。
A是B是C是D是16.在下面的方格中,每行、每列都有1-4这四个数,并且每个数在每行、每列都只出现一次。
B应该是。
17.在下边的方格中,每行、每列都有1、2、3、4这四个数字,并且每个数字在每行、每列都只出现一次。

2023-2024年人教版六年级下册数学小升初分班考专题:探索规律一、单选题1.用3根小棒可以摆一个三角形,按下面的方式摆下去,摆100个三角形需要( )根小棒.A.3×1 00 B.3×50+50+1C.2×99+1 D.3×100﹣1002.有一列数,第一个数是16,第二个数是8,从第三个数开始,每个数都是它前面两个数的平均数,则第2010个数的整数部分是( ) A.8 B.9C.10D.113.按的方式摆放在桌面上.8个按这种方式摆放,有( )个面露在外面.A.20B.23C.26D.294.用6根小棒可以拼成1个正六边形,用11根小棒可以拼成2个正六边形,用16根小棒可以拼3个正六边形,照这样拼下去,用46根可以拼( )个正六边形.A.6B.7C.8D.95.根据15×15=225,25×25=625,35×35=1225,45×45=2025可以推算出65×65=( )A.3025B.4225C.5625D.72256.木材厂将木头按下图堆放,第五堆有( )个.A.15B.21C.28D.34二、填空题7.2000多年前,古希腊毕达哥拉斯在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类(如图),1,3,6,10……由于这些数能够表示成三角形,将其称为三角形数。
按照这样的规律,第11个三角形数有 个小石子。
8.如图,下面是一些小正方形组成的图案,按照规律继续往下画,第5个图案有 个小正方形组成。
9.按下图的规律排列,第一个图形由4张卡片组成,第四个图形由 张卡片组成。
10.如果将一个边长为3的正方形四周涂上红色的框,然后剪成9个小正方形,则小正方形会有三种情况:第一种是两边有红框:第二种是一边有红框:第三种是四边都没有红框。
如果按上述方法要想得到一边有框的小正方形200个,这个正方形的边长应该为 。

小升初数学找规律练习题目班级姓名等级1、观看下面旳几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…依照你所发觉旳规律,请你直截了当写出下面式子旳结果: 1+2+3+…+99+100+99+…+3+2+1=﹏﹏﹏﹏。
2、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+3、以下等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102; …………由此规律知,第⑤个等式是。
4、观看以下等式:221 2111222222223332 ⨯⨯⨯⨯⨯⨯2+=(+)+=(+)3+=(+)……那么第n 个等式能够表示为。
5、212212+=⨯,323323+=⨯,434434+=⨯,……,假设10b a10b a +=⨯〔a 、b 差不多上正整数〕,那么a+b 旳最小值是﹏。
6、如图是用火柴棍摆成边长分别是1、2、3根火柴棍时旳正方形,当边长为n 根火柴棍时,假设摆出旳正方形所用旳火柴棍旳根数为S ,那么S =〔用含n 旳代数式表示,n 为正整数〕、三层二杈树二层二杈树一层二杈树7、如图是五角星灯连续旋转闪耀所成旳三个图形。
照此规律闪耀,下一个呈现出来旳图形是8、如下图是小明用火柴搭旳1条、2条、3条“金鱼”……,那么搭n 条“金鱼”需要火柴根。
……9、如图,在图1中,互不重叠旳三角形共有4个,在图2中,互不重叠旳三角形共有7个,在图3中,互不重叠旳三角形共有10个,……,那么在第n 个图形中,互不重叠旳三角形共有个〔用含n 旳代数式表示〕。
10、小旳黑、白两种颜色旳棋子摆设如下图所示旳正方形图案,那么第n 个图案需要用白色棋子〔〕枚〔用含有n 旳代数式表示〕 11、右图是一回形图,其回形通道旳宽和OB 旳长均为1,回形线与射线OA 交于,,,321A A A …、假设从O 点到1A 点旳回形线为第1圈〔长为7〕,从1A 点到2A 点旳回形线为第2圈,…,依此类推、那么第10圈旳长为。
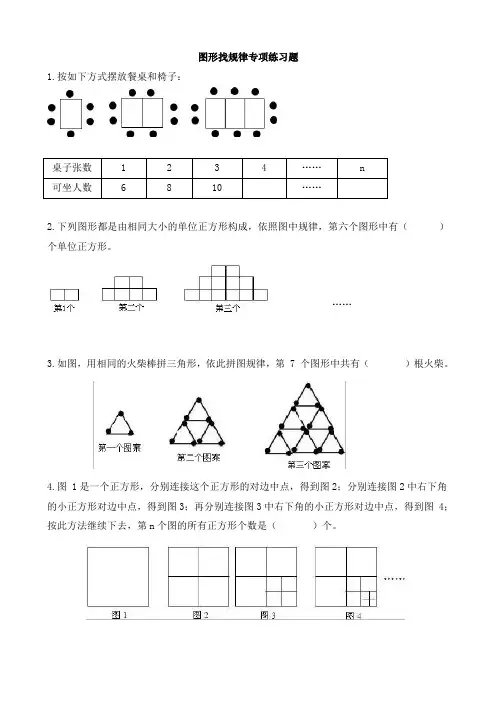
图形找规律专项练习题1.按如下方式摆放餐桌和椅子:桌子张数1234……n可坐人数6810……2.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有()个单位正方形。
……3.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有()根火柴。
4.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是()个。
5.观察下列图案∶它们是按照一定规律排列的,依照此规律,第6个图案中共有()个三角形.6.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形;再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是();第六个正方形的面积是()。
7.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现∶第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有____个小正方形.8.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为9.为庆祝"六一"儿童节,幼儿园举行用火柴棒摆"金鱼"比赛,如图所示,则摆n条"金鱼"需用火柴棒的根数为_____10.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_____个交点,二十条直线相交最多有___个交点11.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表∶图形编号(1)(2)(3)……(n)火柴根数12.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色,的正三角开);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形,如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是()。

小升初找规律专项训练1.观察下列图形,则第n 个图形中三角形的个数是( )2.把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止。
那么2007,2008,2009,2010这四个数中______________可能是剪出的纸片数3.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.第n 个( )4.221.4135-=⨯; 222.5237-=⨯; 223.6339-=⨯224.74311-=⨯…………则第n (n 是正整数)个等式为________.5.王婧同学用火柴棒摆成三个“中”字形图案,依此规律,第n 个“中”字形图案需 根火柴棒( ).6.如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________第1个图形第2个图形第3个图形第4个图形………第1个第2个第3个7.请写出第20行,第21列的数字.8.图6是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案中由个基础图形组成.9.观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有()个.10.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n个图中所贴剪纸“○”的个数为.(1)(2)(3)…………第一行第二行第三行第四行第五行第一列第二列第三列第四列第五列1 2 5 10 17 …4 3 6 11 18 …9 8 7 12 19 …16 15 14 13 20 …25 24 23 22 21 ………图8图6(1) (2) (3)……第1个第2个第3个11.观察下表,回答问题:第个图形中“△”的个数是“○”的个数的5倍.12.将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第 行第 列.13.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .14.观察下列一组数:21,43,65,87,…… ,它们是按一定规律排列的. 那么这一组数的第k 个数是 .序号1 2 3 …图形…第1列 第2列 第3列 第4列 第1行 1 2 3 第2行 6 5 4 第3行 7 8 9 第4行 12 11 10 ……。

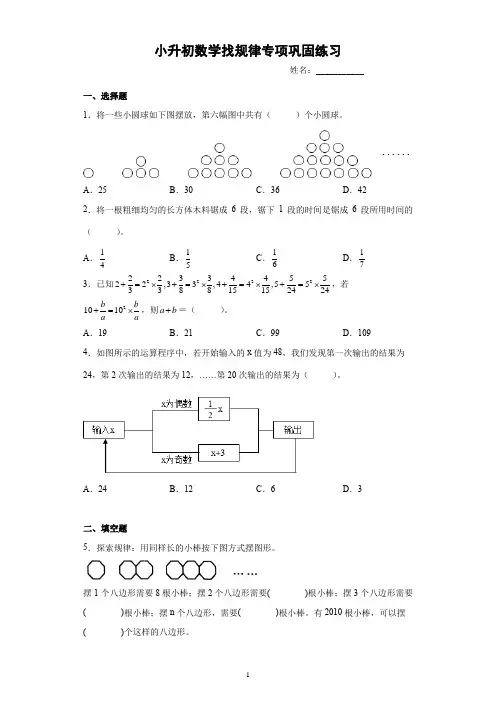
小升初数学找规律专项巩固练习姓名:___________一、选择题1.将一些小圆球如下图摆放,第六幅图中共有( )个小圆球。
A .25B .30C .36D .422.将一根粗细均匀的长方体木料锯成6段,锯下1段的时间是锯成6段所用时间的( )。
A .14B .15C .16D .173.已知22222233445522,33,44,55338815152424+=⨯+=⨯+=⨯+=⨯,若21010b ba a+=⨯,则a b +=( )。
A .19B .21C .99D .1094.如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第2次输出的结果为12,……第20次输出的结果为( )。
A .24B .12C .6D .3二、填空题5.探索规律:用同样长的小棒按下图方式摆图形。
摆1个八边形需要8根小棒;摆2个八边形需要( )根小棒;摆3个八边形需要( )根小棒;摆n 个八边形,需要( )根小棒。
有2010根小棒,可以摆( )个这样的八边形。
6.阅览室摆放了一些长桌用于阅读课外书(如图),每张长桌单独摆放时,最多可供6人同时阅读;两张长桌连接摆放时,最多可供10人同时阅读;三张长桌连接摆放时,最多可供14人同时阅读。
(1)按照这种摆法,完成下表。
(2)按这种摆法,摆放8张长桌,最多可供( )人同时阅读。
(3)按这种摆法,摆放n张长桌,最多可供( )人同时阅读。
7.用黑白两种颜色的正六边形地面砖按如下所示的规律拼成若干个图案:则第⑥个图案中有白色地面砖( )块;第个图案中有白色地面砖( )块。
8.每一个多边形都可以按下图的方法分割成若干个三角形,那么用同样的方法,n边形又能分割成( )个三角形。
9.现有若干个圆环,它们的外直径都是5厘米,环宽5毫米,将它们扣在一起(如图所示)拉紧后测量总长度。
圆环个数1234…总长度591317…(cm)像这样,10个圆环拉紧后的长度是( )厘米。

名校真题测试卷找规律篇时间:15 分钟满分 5 分姓名_________ 测试成绩________1 (12 年清华附中考题)如果将八个数14,30,33,35,39,75,143,169 平均分成两组,使得这两组数的乘积相等,那么分组的情况是什么?2 (13 年三帆中学考题)4+5=9;9+7=16 ;16+9=25 ;25+11=36 这五道算式,观察1+3=4 ;找出规律,然后填写2001 2+()=2002 23 (12 年西城实验考题)一串分数:1,21,2,3,4,1,2,3,4,5,6 7,1,2................................ 8, 1, 2 , ............ ,其中的第2000个分数3 3,5 5 5 5 7 7 7 7 7 7 9 9 9 11 11(1) 请你说明:11 这个数必须选出来;(2) 请你说明:37和73这两个数当中至少要选出一个;(3) 你能选出55 个数满足要求吗?附答案】1 【解】分解质因数,找出质因数再分开,所以分组为33 、35、30、169 和14、39、75、4 (12 年东城二中考题)在2、3 两数之间, 第一次写上5, 第二次在2、5 和5、3 之间分别写上7、8(如下所示), 每次都在已写上的两个相邻数之间写上这两个相邻数之和. 这样的过程共重复了六次, 问所有数之和是多少?2⋯⋯7⋯⋯5⋯⋯8⋯⋯35 (04 年人大附中考题)请你从01、02、03、⋯、98、99中选取一些数,使得对于任何由0~9 当中的某些数字组成的无穷长的一串数当中,都有某两个相邻的数字,是你所选出的那些数中当中的一个。
为了达到这些目的。
143。
2 【解】上面的规律是:右边的数和左边第一个数的差正好是奇数数列3、5、7 、9 、11所以下面括号中填的数字为奇数列中的第2001 个,即4003。
3 【解】分母为 3 的有 2 个,分母为4 个,分母为7 的为 6 个,这样个数2+4+6+8⋯88=1980<2000,这样2000个分数的分母为89,所以分数为20/89 。
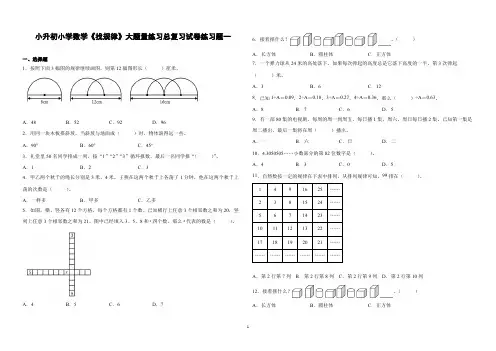
小升初小学数学《找规律》大题量练习总复习试卷练习题一一、选择题1.按照下面3幅图的规律继续画图,则第12幅图形长()厘米。
A.48B.52C.92D.962.用同一块木板搭斜坡,当斜坡与地面成()时,物体滚得远一些。
A.90°B.60°C.45°3.礼堂里50名同学排成一列,按“1”“2”“3”循环报数,最后一名同学报“()”。
A.1B.2C.34.甲乙两个秋千的绳长分别是3米、4米。
王燕在这两个秋千上各荡了1分钟,他在这两个秋千上荡的次数是()。
A.一样多B.甲多C.乙多5.如图,横、竖各有12个方格,每个方格都有1个数。
已知横行上任意3个相邻数之和为20,竖列上任意3个相邻数之和为21。
图中已经填入3、5、8和x四个数,那么x代表的数是()。
A.4B.5C.6D.76.接着摆什么?。
()A.长方体B.圆柱体C.正方体7.一个弹力球从24米的高处落下,如果每次弹起的高度总是它落下高度的一半,第3次弹起()米。
A.3B.6C.128.已知1÷A=0.09,2÷A=0.18,3÷A=0.27,4÷A=0.36,那么()÷A=0.63。
A.8B.7C.6D.59.有一部80集的电视剧,每周的周一到周五,每日播1集,周六、周日每日播2集。
已知第一集是周二播出,最后一集将在周()播出。
A.一B.六C.日D.二10.4.3050505……小数部分的第82位数字是()。
A.4B.3C.0D.511.自然数按一定的规律在下表中排列,从排列规律可知,99排在()。
A.第2行第7列B.第2行第8列C.第2行第9列D.第2行第10列12.接着摆什么?。
()A.长方体B.圆柱体C.正方体13.照这样摆下去,第6幅点子图有()个点子。
A.12B.13C.14D.1514.有两个秋千,小红分别在两个秋千上荡了1分钟。
小红1分钟内荡秋千的次数与()有关。
名校真题 测试卷 找规律篇1 (清华附中考题)如果将八个数14,30,33,35,39,75,143,169平均分成两组,使得这两组数的乘积相等,那么分组的情况是什么?2 (三帆中学考题) 观察1+3=4 ; 4+5=9 ; 9+7=16 ; 16+9=25 ; 25+11=36 这五道算式,找出规律, 然后填写2001+( )=20023 (西城实验考题)一串分数:其中的第2000个分数是 .2212123412345612812,,,,,,,,,,,,.....,,,......,33,555577777799911114 (东城二中考题)在2、3两数之间,第一次写上5,第二次在2、5和5、3之间分别写上7、8(如下所示),每次都在已写上的两个相邻数之间写上这两个相邻数之和.这样的过程共重复了六次,问所有数之和是多少?2......7......5......8 (3)5 (人大附中考题)请你从01、02、03、…、98、99中选取一些数,使得对于任何由0~9当中的某些数字组成的无穷长的一串数当中,都有某两个相邻的数字,是你所选出的那些数中当中的一个。
为了达到这些目的。
(1)请你说明:11这个数必须选出来;(2)请你说明:37和73这两个数当中至少要选出一个;(3)你能选出55个数满足要求吗?【附答案】1 【解】分解质因数,找出质因数再分开,所以分组为33、35、30、169和14、39、75、143。
2 【解】上面的规律是:右边的数和左边第一个数的差正好是奇数数列3、5、7、9、11……,所以下面括号中填的数字为奇数列中的第2001个,即4003。
3 【解】分母为3的有2个,分母为4个,分母为7的为6个,这样个数2+4+6+8…88=1980<2000,这样2000个分数的分母为89,所以分数为20/89。
4 【解】:第一次写后和增加5,第二次写后的和增加15,第三次写后和增加45,第四次写后和增加135,第五次写后和增加405,……它们的差依次为5、15、45、135、405……为等比数列,公比为3。
小升初真题之找规律篇1 (西城实验考题)有一批长度分别为 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 和 11 厘米的细木条,它们的数量都足够多,从中适当选取 3 根木条作为三条边,可围成一个三角形 ;如果规定底边是 11 厘米,你能围成多少个不同的三角形?2 (三帆中学考题)有 7 双白手套, 8 双黑手套, 9 双红手套放在一只袋子里。
一位小朋友在黑暗中从袋中摸取手套,每次摸一只,但无法看清颜色,为了确保能摸到至少 6 双手套,他最少要摸出手套( )只。
(手套不分左、右手,任意二只可成一双 ) 。
3 (人大附中考题)某次中外公司谈判会议开始 10 分钟听到挂钟打钟 (只有整点时打钟,几点钟就响几下),整个会议当中共听到 14 下钟声,会议结束时,时针和分针恰好成 90 度角,求会议开始的时间结束的时间及各是什么时刻。
4 (101 中学考题)4 道单项选择题,每题都有 A、B 、C 、D 四个选项,其中每题只有一个选项是正确的,有800 名学生做这四道题,至少有 _________人的答题结果是完全一样的?5 (三帆中学考题)设有十个人各拿着一只提桶同时到水龙头前打水,设水龙头注满第一个人的桶需要 1 分钟,注满第二个人的桶需要 2 分钟,…… .如此下去,当只有两个水龙头时,巧妙安排这十个人打水,使他们总的费时时间最少 .这时间等于_________分钟.预测 1在右图的方格表中,每次给同一行或同一列的两个数加 1,经过若干次后,能否使表中的四个数同时都是 5 的倍数?为什么?1 24 3预测 2甲、乙两厂生产同一规格的上衣和裤子,甲厂每月用 16 天生产上衣, 14 天做裤子,共生产448 套衣服(每套上衣、裤子各一件);乙厂每月用 12 天生产上衣, 18 天生产裤子,共生产720 套衣服。
两厂合并后,每月(按 30 天计算)最多能生产多少套衣服?找规律篇之答案1 (西城实验考题)【解】由于数量足够多,所以考虑重复情况;现在底边是 11,我们要保证的是两边之和大于第三边,这样我们要取出的数字和大于 11.情况如下:一边长度取 11,另一边可能取 1~11 总共 11 种情况;一边长度取 10,另一边可能取 2~10 总共 9 种情况;… …一边长度取 6,另一边只能取 6 总共 1 种;下面边长比 6 小的情况都和前面的重复,所以总共有 1+3+5+7+9+11=36 种。
人教版六年级下册数学小升初专题训练:探索规律一、单选题1.下图中每个小正方形的棱长都是2cm,如下图摆法,( )个正方体摆成的长方体表面积是808平方厘米?A.25B.50C.100D.2002.用小棒按照下面的方式摆图形。
像这样,连着摆5个正六边形需要( )根小棒。
A.26B.21C.31D.363.如图是由大小相同的棋子按照一定规律排列组成的图形,摆第1个图需要6枚棋子,摆第2个图需要9枚棋子,摆第3个图需要12枚棋子,……按此规律,摆第32个图需要( )枚棋子。
A.93B.96C.99D.1024.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )A.13=3+10B.25=9+16C.36=15+21D.49=18+315.如图,1 个正方形有4 个顶点,2 个正方形有7 个顶点,3 个正方形有10 个顶点。
像这样摆下去,摆n个正方形,有( )个顶点。
A.4n-1B.4n+1C.3n+1D.3n-1二、判断题6.在2、5、11、20、Y、47、65……这列数中,Y表示一个任意的自然数。
( )7.用火柴棒按下图所示搭正方形,搭一个正方形用4根火柴棒,搭n个正方形用4n根火柴棒。
( )8.因为1÷A=0.0909…;2÷A=0.1818…;3÷A=027272…;所以4÷A=0.3636…。
( )9.一根木头长10m,要把它平均分成5段,每锯下一段需要8分钟,锯完一共要花40分钟。
( )10.○▲□○▲□○▲□……,按照这样的规律摆,第20个图形是▲。
()三、填空题11.找规律填数:1、2、4、7、11、 。
2、4、8、16、 。
12.如图,像这样把同样的杯子叠在一起,3 只共高18 厘米,5只共高24厘米,一只杯子高 厘米,9只杯子叠起来高 厘米。
(小升初高频考点)探索规律(专项训练)2022-2023学年六年级下册数学人教版一.选择题(共9小题)1.(2022•睢县)找规律:4,9,16,25,____,49;横线的数是()A.28B.36C.452.(2022•西山区)有三个正整数。
如果其中两个数的平方的和等于第三个数的平方,那么这三个数就是勾股数。
例如:3、4、5这三个数,因为32=9;42=16;52=25,可以计算得出32+42=52,所以3、4、5是勾股数。
运用上述信息进行判断。
下列选项中是勾股数的是()A.1、2、3B.6、8、10C.3、5、7D.2、2、4 3.(2022•岳阳)按如图所示的方式排列点阵,则第六个点阵中有()个点。
A.16B.21C.25D.36 4.(2020•涟水县)将正整数按如图的位置顺序排列:根据排列规律,则2020应在()A.A处B.B处C.C处D.D处5.(2022•唐山)按3个红球、4个白球、5个黄球的顺序排列180个球,第160个球是()A.红球B.白球C.黄球D.不确定6.(2020•广宁县)9个点可以连()条线段。
A.27B.10C.36D.18 7.(2022•神木市)如图,连接在一起的两个正方形,边长都是1分米。
一个微型机器人由A处开始,按ABCDEFCGABCDEFCG…的顺序,沿正方形的边循环移动。
当微型机器人移动了2019分米时,它停在()处。
A.A B.B C.C D.D8.(2022•固始县)找规律:1,4,9,16,……,第6个数是()A.25B.36C.499.(2022•魏县)根据6×9=54,66×99=6534,666×999=665334,可知6666×9999=()A.66653334B.6666533334C.6665553334二.填空题(共8小题)10.(2022•九江)将321化成小数后,小数点后第1980位上的数字是.11.(2022•黔东南州)有一列数:2,1,3,5,2,1,3,5,…第174个数是,这174个数相加的和是。
小升初专项训练 找规律篇一、小升初考试热点及命题方向找规律问题在小升初考试中几乎每年必考,但考题的分值较低,多以填空题型是出现。
在刚刚结束的小升初选拔考试中,人大附中,首师附中,十一学校,西城实验,三帆,西外,东城二中和五中都涉及并考察了这一类题型。
二、2018年考点预测18年的这一题型必然将继续出现,题型的出题热点在利用通项表达式(即字母表示)总结出已知条件中等式的内在规律和联系,这一类题型主要考察学生根据已有条件进行归纳与猜想的能力,希望同学们多加练习。
1 与周期相关的找规律问题【例1】、(★★)7n 化小数后,小数点后若干位数字和为1992,求n 为多少? 【解】7n 化小数后,循环数字和都为27,这样1992÷27=73…21,所以n=6。
【例2】、(★★)有一数列1、2、4、7、11、16、22、29……那么这个数列中第2006个数除以5的余数为多少?【解】数列除以5的余数为1、2、4、2、1、1、2、4、2、1…这样就使5个数一周期,所以2003÷5=400…3,所以余4。
【例3】、(★★★)某人连续打工24天,赚得190元(日工资10元,星期六做半天工,发半工资,星期日休息,无工资).已知他打工是从1月下旬的某一天开始的,这个月的1号恰好是星期日. 问:这人打工结束的那一天是2月几日?【来源】 第五届“华杯赛”初赛第16题【解】因为3×7<24<4×7,所以24天中星期六和星期日的个数,都只能是3或4.又,190是10的整数倍。
所以24天中的星期六的天数是偶数.再由240-190=50(元),便可知道,这24天中恰有4个星期六、3个星期日.星期日总是紧接在星期六之后的,因此,这人打工结束的那一天必定是星期六.由此逆推回去,便可知道开始的那一天是星期四.因为1月1日是星期日,所以1月22日也是星期日,从而1月下旬唯一的一个星期四是1月26日.从1月26日往后算,可知第24天是2月18日,这就是打工结束的日子.2 图表中的找规律问题【例4】、(★★)图中,任意_--个连续的小圆圈内三个数的连乘积郡是891,那么B=_______.【来源】第十届<小数报>数学竞赛初赛填空题第5题【解】根据“任意三个连续的小圆圈内三个数的连乘积都是891”,可知任意一个小圆圈中的数和与它相隔2个小圆圈的小圆圈中的数是相同的.于是,B=891÷(9×9)=11.【例5】(★★★)自然数如下表的规则排列:求:(1)上起第10行,左起第13列的数;(2)数127应排在上起第几行,左起第几列?【解】:本题考察学生“观察—归纳—猜想”的能力.此表排列特点:①第一列的每一个数都是完全平方数,并且恰好等于所在行数的平方;②第一行第n个数是(n-1)2+1,②第n行中,以第一个数至第n个数依次递减1;④从第2列起该列中从第一个数至第n个数依次递增1.由此(1)〔(13-1)2+1〕+9=154;(2)127=112+6=〔(12-1)2+1〕+5,即左起12列,上起第6行位置.3较复杂的数列找规律【例6】、(★★★)设1,3,9,27,81,243是6个给定的数。
六年级小升初找规律练习题题目1:请找出下列数字序列中的规律并填写正确的数。
1, 4, 9, 16, _____解析:观察数字序列,可以发现每个数都是前一个数的平方。
因此,下一个数应该是25。
答案:25题目2:在下列数字序列中找出规律并填写缺失的数。
2, 4, 8, 16, __, 64解析:观察数字序列,可以发现每个数都是前一个数的2倍。
因此,下一个数应该是32。
答案:32题目3:请找出下列数字序列中的规律并填写正确的数。
3, 6, 9, 12, 15, ____解析:观察数字序列,可以发现每个数都是前一个数加上3。
因此,下一个数应该是18。
答案:18题目4:在下列数字序列中找出规律并填写缺失的数。
10, 18, 26, __, 42, 50解析:观察数字序列,可以发现每个数都是前一个数加上8。
因此,缺失的数应该是34。
答案:34题目5:请找出下列数字序列中的规律并填写正确的数。
1, 3, 6, 10, 15, ____解析:观察数字序列,可以发现每个数都是前一个数加上一个递增的数。
观察差值序列1, 2, 3, 4,可以发现这个差值序列是递增的自然数序列。
因此,下一个数应该是21。
答案:21题目6:在下列数字序列中找出规律并填写缺失的数。
5, 10, 20, __, 80, 160解析:观察数字序列,可以发现每个数都是前一个数的2倍。
因此,缺失的数应该是40。
答案:40题目7:请找出下列数字序列中的规律并填写正确的数。
1, 1, 2, 3, 5, 8, ____解析:观察数字序列,可以发现从第3个数开始,每个数都是前两个数的和。
因此,下一个数应该是13。
答案:13题目8:在下列数字序列中找出规律并填写缺失的数。
2, 5, 8, __, 14, 17解析:观察数字序列,可以发现每个数都是前一个数加上3。
因此,缺失的数应该是11。
答案:11题目9:请找出下列数字序列中的规律并填写正确的数。
1, 4, 9, 16, 25, ____解析:观察数字序列,可以发现每个数都是前一个数的平方。