第五章 虚拟变量

第五章 虚拟变量复习题一、单项选择题 1、虚拟变量( A )A.主要来代表质的因素，但在有些情况下可以用来代表数量因素B.只能代表质的因素C.只能代表数量因素D.只能代表季节影响因素2、设某地区消费函数中，消费支出不仅与收入x 有关，而且与消费者的年龄构成有关，若将年龄构成分为小孩、青年人、成年人和老年人4个层次。

假设边际消费倾向不变，考虑上述年龄构成因素的影响时，该消费函数引入虚拟变量的个数为 （ C ）A 1个B 2个C 3个D 4个3、在经济发展发生转折时期，可以通过引入虚拟变量方法来表示这种变化。

例如，研究中国城镇居民消费函数时。

1991年前后，城镇居民商品性实际支出Y 对实际可支配收入X 的回归关系明显不同。

现以1991年为转折时期，设虚拟变量⎩⎨⎧=年以后；年以前；1991019911t D ，数据散点图显示消费函数发生了结构性变化：基本消费部分下降了，边际消费倾向变大了。

则城镇居民线性消费函数的理论方程可以写作：（ D ）。

A 、ttt u XY ++=10ββB 、ttt tt u XD XY +++=210βββC 、tt tt u D XY +++=210βββD 、ttt t tt u XD D XY ++++=3210ββββ4、对于含有截距项的计量经济模型，若想将含有m 个互斥类型的定性因素引入到模型中，则应该引入虚拟变量个数为 （ B ） A m B m-1 C m+1 D m-k5、对于一个回归模型中不包含截距项，若将一个具有m 个特征的质的因素引入进计量经济模型，则虚拟变量数目为( A ) A.m B.m-1C.m-2D.m+1 6、设某计量经济模型为：ii i u D Y ++=βα，其中iY 大学教授年薪，⎩⎨⎧=女教授男教授01i D ，则对于参数α、β的含义，下列解释不正确的是（ B ）A. α表示大学女教授的平均年薪；B. β表示大学男教授的平均年薪；C. α+ β表示大学男教授的平均年薪；D. β表示大学男教授和女教授平均年薪的差额7、个人保健支出的计量经济模型：iii i XD Y μβαα+++=221 ，其中iY 保健年度支出；iX个人年度收入；虚拟变量⎩⎨⎧=大学以下大学及以上012i D ；iμ满足古典假定。

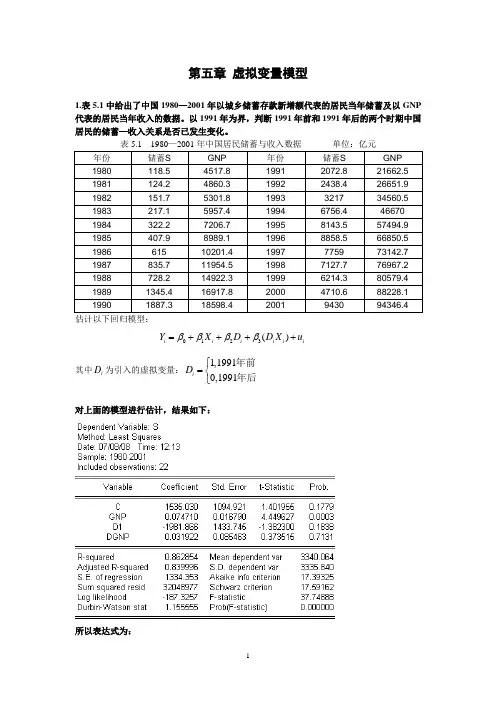
第五章虚拟变量模型1.表5.1中给出了中国1980—2001年以城乡储蓄存款新增额代表的居民当年储蓄及以GNP 代表的居民当年收入的数据。

以1991年为界，判断1991年前和1991年后的两个时期中国居民的储蓄—收入关系是否已发生变化。

年份储蓄S GNP 年份储蓄S GNP 1980 118.5 4517.8 1991 2072.8 21662.5 1981 124.2 4860.3 1992 2438.4 26651.9 1982 151.7 5301.8 1993 3217 34560.5 1983 217.1 5957.4 1994 6756.4 46670 1984 322.2 7206.7 1995 8143.5 57494.9 1985 407.9 8989.1 1996 8858.5 66850.5 1986 615 10201.4 1997 7759 73142.7 1987 835.7 11954.5 1998 7127.7 76967.2 1988 728.2 14922.3 1999 6214.3 80579.4 1989 1345.4 16917.8 2000 4710.6 88228.1 1990 1887.3 18598.4 2001 9430 94346.4 估计以下回归模型：0123()i i i i i iY X D D X uββββ=++++其中iD为引入的虚拟变量：1,19910,1991iD⎧=⎨⎩年前年后对上面的模型进行估计，结果如下：所以表达式为：15350.0751981.90.032()i i i i i Y X D D X =+-+(1.40) (4.45) (-1.38) (0.37)从2β和3β的t 检验值可以知道，这两个参数显著的为0，所以1991年前和1991年后两个时期的回归结果是相同的。

下面用邹式检验来验证上面对于两个时期的回归结果相同的结论是否正确。

王中昭制作主要内容：§5.1 虚拟变量模型第五章经典单方程计量经济学模型：专门问题§5.1 、虚拟变量模型王中昭制作一、什么叫虚拟变量•在回归模型中，除了定量变量外，有时还必须引入一些不可量化的经济变量，例如，研究职工的收入问题，需考虑到职工的受教育程度，研究冷饮的需求量或某个旅游胜地的旅游人数，需引入季节因素。

这些都是非量化因素，但又非常重要，需引入模型中。

这些不可量化因素可称为虚拟变量。

•一般地，在模型中的定性变量称为虚拟变量。

或称为二元变量或分类变量等等。

用D表示虚拟变量，以强调它与其它定量变量的区别。

二、引入虚拟变量的方式与特点王中昭制作•①、加法方式：虚拟变量与各解释变量之间存在相加关系。

•特点：模型的截距不同，斜率相同。

•例如：Y=a1+a2D t+b1X t+μtt•当D=1时，截距=a1+a2；t•当D=0时，截距=a1t•②、乘法方式：虚拟变量与各解释变量之间存在相乘关系。

•特点：模型的截距相同，斜率不同。

•例如：Y=a1+ b1X t+b2D t*X t+μtt•当D=1时，斜率=b1+b2；t•当D=0时，斜率=b王中昭制作•③、混合方式：虚拟变量与各解释变量之间同时存在相乘和相加关系。

•特点：模型的截距和斜率均不相同。

•例如：Y t=a1+a2D t+b1X t+b2D t*X t+μt•当Dt =1时，截距=a1+a2，斜率=b1+b2；•当Dt=0时，截距=a1，斜率=b1。

王中昭制作•还可将多个虚拟变量引入模型中以考察多种“定性”因素的影响。

一个以性别为虚拟变量考察企业职工薪金的模型：D 1为性别，D 2为学历。

ii i D D X Y μββββ++++=231210⎩⎨⎧=012D 本科及以上学历本科以下学历职工薪金的加法方式引入的模型为：其中：Y 为企业职工的薪金，X 为工龄，D 1=1，若是男性，D 1=0，若是女性。

王中昭制作引入虚拟变量的作用是：消除异常值、体现其它重要的非量化因素对因变量的影响（如：转折点、季节因素、政策因素、教育程度、民族、性别、地区和资料分组等）、提高模型的可靠性。

Econometrics第五章虚拟变量回归模型（教材第六章）第五章虚拟变量回归模型第一节虚拟变量的性质和引入的意义第二节虚拟变量的引入第三节交互作用效应第四节含虚拟变量的回归模型学习要点虚拟变量的性质，虚拟变量的设定5.1 虚拟变量的性质和引入的意义虚拟变量的性质f定性变量性别（男，女）婚姻状况（已婚，未婚）受教育程度（高等教育，其他）收入水平（高收入，中低收入）肤色（白人，有色人种）政治状况（和平时期，战争时期）f引入虚拟变量（Dummy Variables）1、分离异常因素的影响，例如分析我国GDP的时间序列，必须考虑“文革”因素对国民经济的破坏性影响，剔除不可比的“文革”因素。

2、检验不同属性类型对因变量的作用，例如工资模型中的文化程度、季节对销售额的影响。

3、提高模型的精度，相当与将不同属性的样本合并，扩大了样本量，从而提高了估计精度）。

5.1 虚拟变量的性质和引入的意义5.2 虚拟变量的引入虚变量引入的方式主要有两种f加法方式虚拟变量与其它解释变量在模型中是相加关系，称为虚拟变量的加法引入方式。

加法引入方式引起截距变动5.2 虚拟变量的引入f 虚拟变量的作用在于把定性变量“定量化”：通过赋值0和1，0表示变量不具备某种性质，1表示具备。

f 例，0代表男性，1代表女性；0代表未婚，1代表已婚；等等。

f 这类取值为0和1的变量称为虚拟变量（dummy variables ），通常用符号D 表示。

f 事实上，模型可以只包括虚拟变量（ANOVA 模型）：其中，0,1,i i D D ==男性；女性。

12i i iY B B D u =++5.2 虚拟变量的引入虚拟变量的性质f 假定随机扰动项满足男性的期望：5.2 虚拟变量的引入虚拟变量的性质f 食品支出对性别虚拟变量（男=0，女=1）回归的结果：f 结果怎么解释？f 由于男性赋值为0，女性赋值为1，因此，截距项表示取值为0的一类（这里是男性）的均值。