四则运算的意义和各部分名称(第一课时)

（完整版）四则运算知识点四则运算一、四则运算的意义1、加法：（1）加法的意义：把两个数合并成一个数的运算叫做加法。

小数、分数加法与整数加法的意义完全相同。

（在加法算式中，加号两边的数叫做加数，等号后面的数叫做和。

）（2）加法各部分之间的关系：加数 + 加数 = 和和－一个加数 = 另一个加数2、减法：（1）减法的意义：已知两个加数的和与其中的一个加数，求另一个加数的运算叫做减法。

小数、分数减法与整数减法的意义完全相同。

（在减法算式中，减号前面的数叫做被减数，减号后面的数叫做减数，等号后面的数叫做差。

）（2）减法个部分的关系：被减数－减数=差减数＋差 = 被减数被减数－差 = 减数3、乘法：（1）乘法的意义：求几个相加数的和的简便运算叫做乘法。

小数、分数乘整数的意义与整数乘法的意义相同。

（在乘法算式中，乘号两边的数叫做因数，等号后面的数叫做积。

）一个数乘分数的意义，就是求这个数的几分之几是多少。

一个数乘小数的意义，就是不求这个数的十分之几、百分之几、千分之几……是多少。

（1）乘法各部分的关系：因数×因数 = 积积÷一个因数 = 另一个因数4、除法：（1）除法的意义：已知两个因数的积，与其中的一个因数，求另一个因数的运算叫做除法。

小数、分数除法和整数除法意义相同。

（在除法算式中，除号前面的数叫做被除数除数，除号后面的数叫做除数，等号后面的数叫做商。

）（2）除法各部分的关系：被除数÷除数 = 商除数×商 = 被除数被除数÷商 = 除数（3）有余数的除法各部分的关系：商×除数＋余数 = 被除数5、四则运算的方法（1）整数、小数加减法的计算方法加法：相同数位对齐，从低位加起，哪一位相加满十，要向前一位进一。

减法：相同数位对齐，从低位减起，哪一位上不够减，就向前一位退一作十再减。

（2）整数、小数、分数乘法的计算方法整数、小数乘法计算方法基本相同，都是把末位数字对齐，从低位起，依次用下面个因数每上的数去乘上面个因数，用哪一位上的数去乘，乘得的积的末尾就和那一位对齐，最后再把几次乘得的积相加。

一、四则运算►教案◄本单元主要教学加法、减法的意义及各部分间的关系，乘法、除法的意义及各部分间的关系，让学生了解加、减、乘、除四则运算的意义及运算顺序，了解小括号、中括号的作用及有关0的运算。

教材一开始就教学加法、减法的意义，再教学乘法、除法的意义，让学生对加、减、乘、除有个系统的认识，接着在四则运算中介绍了小括号、中括号的作用，让学生弄清混合运算的运算顺序，正确地进行计算。

教学中加强了数学与生活之间的联系，提高了学生的学习兴趣，还在例5中安排了租船最省钱的问题，让学生在小组合作中探究学习，灵活解决租船问题，提高学生分析、解决问题的能力。

在此之前，学生已经学会按从左往右的顺序计算两步式题，并且知道小括号的作用，这里主要教学四则运算的意义和含有小括号、中括号的两级运算的运算顺序，并对此前学习过的加、减、乘、除法的知识和四则混合运算进行较为系统的梳理、概括和总结。

1．进一步掌握加、减、乘、除法的意义及各部分之间的关系。

2．学会含有小括号、中括号的两级运算的运算顺序。

3．使学生在解决实际问题的过程中，养成认真审题、独立思考等学习习惯。

引导学生归纳出加、减、乘、除法各部分之间的关系，总结出有括号的两级运算的运算顺序。

1．正确运用加、减、乘、除各部分之间的关系解答问题。

2．会用小括号、中括号列综合算式。

3．灵活制订租船最省钱的方案。

第一课时加、减法的意义和各部分间的关系教材第2、3页例1的内容及练习一。

1．通过算式的变换，理解加、减法的意义，掌握加、减法各部分之间的关系，理解减法是加法的逆运算。

2．能够比较熟练地应用加、减法各部分之间的关系对加、减法进行验算，并能够解决一些简单的实际问题。

3．在探索新知的过程中，进一步培养学生的抽象概括能力。

理解加法、减法的意义。

明确加、减法之间的关系。

一、旧知铺垫1．口算。

155－30800＋32510＋35230＋50 143－24 61－452．说一说。

32＋100表示()150－30表示()3．今天我们继续学习加、减法的意义和各部分间的关系。

第1单元四则运算第1课时加、减法的意义和各部分间的关系【教学内容】教材第2～3页例1及相关练习。

【教学目标】1.结合具体情境经历概括加、减法意义的过程，理解加、减法的意义，掌握加、减法各部分间的关系。

2.在探索加、减法各部分间的关系的过程中，发展抽象意识与概括能力。

3.在用抽象文字表示加、减法各部分间的关系的过程中，感受数学的内在逻辑性，体会数学的价值。

【重点难点】重点：理解加、减法的意义，掌握加、减法各部分间的关系。

难点：学会并熟练运用加减法各部分间的关系来完成算式以解决实际问题。

【教学过程】一、情境导入【课件出示教材第2页主题图】师：你们知道这是什么铁路吗？（学生可能回答不出来。

）师介绍：图中显示的是中国新世纪四大工程之一，也就是青藏铁路。

青藏铁路的建设创造了很多高海拔地区铁路建设的奇迹，今天这节课我们就从数学的角度一起走进青藏铁路。

二、探究新知1.探究加法的意义。

【课件出示教材第2页例1（1）】（1）自主探究。

（2）交流汇报。

师：从题中你知道了什么？预设1：西宁到格尔木的铁路长814km，格尔木到拉萨的铁路长1142km。

预设2：要求西宁到拉萨的铁路长多少千米。

师：你们是如何画图表示题目中的数量关系并列式解答的呢？预设1：预设2：814＋1142＝1956（km）（3）概括加法的意义。

师：为什么要用加法计算？预设：要求西宁到拉萨的铁路长，就是要把西宁到格尔木段与格尔木到拉萨段两段铁路的长度合并成一个数，因此用加法进行计算。

师：想一想，什么是加法？在学生思考、交流后，教师规范学生的表述：把两个加数合并成一个数的运算，叫作加法。

师：你还记得加法算式中各部分的名称吗？请你在这个算式中标出来。

预设：2.探究减法的意义。

【课件出示教材第3页例1（2）、（3）】（1）自主探究。

（2）交流汇报。

师：与第（1）题相比，第（2）、（3）题分别是已知什么？求什么？怎样算？预设1：第（2）题已知西宁到拉萨的铁路全长和西宁到格尔木的铁路长度，求格尔木到拉萨的铁路长度，用减法计算。

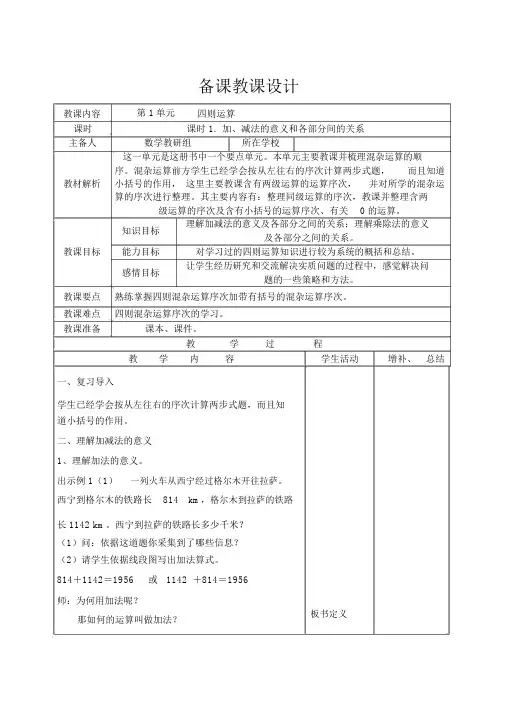
备课教课设计教课内容第 1单元四则运算课时课时 1.加、减法的意义和各部分间的关系主备人数学教研组所在学校这一单元是这册书中一个要点单元。

本单元主要教课并梳理混杂运算的顺序。

混杂运算前方学生已经学会按从左往右的序次计算两步式题，而且知道教材解析小括号的作用，这里主要教课含有两级运算的运算序次，并对所学的混杂运算的序次进行整理。

其主要内容有：整理同级运算的序次，教课并整理含两级运算的序次及含有小括号的运算序次、有关0 的运算。

知识目标理解加减法的意义及各部分之间的关系；理解乘除法的意义及各部分之间的关系。

教课目标能力目标对学习过的四则运算知识进行较为系统的概括和总结。

感情目标让学生经历研究和交流解决实质问题的过程中，感觉解决问题的一些策略和方法。

教课要点熟练掌握四则混杂运算序次加带有括号的混杂运算序次。

教课难点四则混杂运算序次的学习。

教课准备课本、课件。

教学过程教学内容学生活动增补、总结一、复习导入学生已经学会按从左往右的序次计算两步式题，而且知道小括号的作用。

二、理解加减法的意义1、理解加法的意义。

出示例 1（1）一列火车从西宁经过格尔木开往拉萨。

西宁到格尔木的铁路长814km，格尔木到拉萨的铁路长 1142 km。

西宁到拉萨的铁路长多少千米？（1）问：依据这道题你采集到了哪些信息？（2）请学生依据线段图写出加法算式。

814＋1142＝1956或1142 ＋814＝1956师：为何用加法呢？那如何的运算叫做加法？板书定义(3)小结：把两个数合并成一个数的运算，叫做加法。

( 出示加法的意义 )2、理解减法的意义能不可以试着把这道加法应用题改编成减法应用题呢？(1)依据学生的回答，出示例 1（ 2）（3）试试用线段图表示：师：依据线段图写出两道减法算式，并谈谈这样列式的原由。

1956－ 814＝1142或1956－1142＝814(2)问：如何的运算是减法？ ( 小组谈论 )(3)小结：已知两个加数的和与此中的一个加数，求另一个加数的运算，叫做减法。

四则运算知识集结知识元加、减法的意义及各部分间的关系知识讲解知识点一：加减法的意义和各部分间的关系一、加减法的意义1.加法的意义：把两个数合并成一个数的运算，叫做加法；2.减法的意义：已知两个加数的和与其中的一个加数，求另一个加数的运算，叫做减法.二、加减法算式各部分的名称1.加法各部分的名称：相加的两个数叫做加数，加得的数叫做和；2.减法各部分的名称：在减法中，已知的和叫做被减数，已知的一个加数叫做减数，求得的另一个加数叫做差.三、加减法各部分间的关系1.加法各部分间的关系：和=加数+加数，加数=和-另一个加数；2.减法各部分间的关系：差=被减数-减数，减数=被减数-差，被减数=减数+差；3.加减法间的关系：减法是加法的逆运算.例题精讲加、减法的意义及各部分间的关系例1.做一道减法题时，小军把减数的个位上的6看成9，十位上的3看成8，结果差是92，正确的答案应是_____。

例2.被减数减去减数，差是0.4，被减数、减数与差的和是2，减数是_____。

例3.芸芸做加法时，把一个加数的个位上的9看作8，十位上的6看作9，把另一个加数的百位上的5看作4，个位上的5看作9，结果和是1997，正确的结果应该是_____。

例4.'已知被减数、减数和差三个数的和是612，你知道被减数是多少吗？'例5.'叮叮在计算加法时，把一个加数百位上的8看成6，把另一个加数十位上的1错看成4，得到和为923．正确的和是多少？'乘、除法的意义及各部分间的关系知识讲解乘除法的意义和各部分间的关系一、乘除法的意义1.乘法的意义：求几个相同加数的和的简便运算，叫做乘法；2.除法的意义：已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法.二、乘除法算式各部分的名称1.乘法算式各部分的名称：相乘的两个数叫做因数，乘得的数叫做积；2.除法算式各部分的名称：在除法中，已知的积叫做被除数，已知的一个因数叫做除数，求得的数叫做商.三、乘除法各部分间的关系1.乘法各部分间的关系：积=因数×因数，因数=积÷另一个因数；2.乘除法各部分间的关系：（1）没有余数的除法：商=被除数÷除数，除数=被除数÷商，被除数=商×除数；（2）有余数的除法：被除数=商×除数+余数，商=（被除数-余数）÷除数，除数=（被除数-余数）÷商.3.乘除法间的关系：除法是乘法的逆运算.例题精讲乘、除法的意义及各部分间的关系例1.'某手机生产厂原计划5天生产完手机1600部，实际4天就完成了任务，实际每天比原计划多生产多少部？'例2.'冬冬体重38千克，表弟体重是他的一半，而爷爷体重是表弟的4倍。