下载文档原格式
安康市2019－2020学年第一学期高三阶段性考试2019.12物理试题考生注意：1.本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分。
2.考生作答时，请将答案答在答题卡上，答在试卷上无效。
第I 卷(选择题，共40分)一、选择题：本题共10小题，在每小题给出的四个选项中：第1～6题只有一个选项正确，第7～10题有多个选项正确，全部选对的得1分，选对但不全的得2分，有选错的得0分。
1.在水平地面固定倾角为θ的斜面体，质量为m 的物体在平行于底边、大小为F 的水平力作用下静止于斜面上，如图所示。
重力加速度大小为g 。
该物体受到的摩擦力大小为A.FB.F ＋mgC.F ＋mgsin θD.22(sin )F mg θ+2.如图所示，质量不等的甲、乙两个物块放在水平圆盘上，两物块与水平圆盘的动摩擦因数相同，最大静摩擦力等于滑动摩擦力，让圆盘绕过圆心的竖直轴匀速转动，并逐渐增大转动的角速度，结果发现甲物块先滑动，其原因是A.甲的质量比乙的质量小B.甲的质量比乙的质量大C.甲离转轴的距离比乙离转轴的距离小D.甲离转轴的距离比乙离转轴的距离大3.如图所示，三角块B 放在斜面体A 上，轻弹簧一端连接三角块B ，另一端连接在天花板上，轻弹簧轴线竖直，斜面的倾角为30°，若A 的质量为1kg ，B 的质量为0.5kg ，地面对A 的支持力大小为20N ，重力加速度为10m/s 2，则A 对B 的摩擦力大小为A.0B.2.5NC.5N 3N4.一个质点做直线运动，其0～t0时间内的v－t图象如图所示，则在0～t0时间内下列说法正确的是A.质点一直做减速运动B.质点的加速度与速度一直反向C.质点的平均速度为34vD.质点的加速度大小为032vt5.如图所示，在P点斜向上抛出一个小球，要使小球始终垂直打在竖直墙面上，则抛出的初速度大小v和初速度与水平方向的夹角θ的关系，不计空气阻力。
正确的是A.v与sinθ成反比B.v与tanθ成正比C.v2与sin2θ成反比D.v2与cos2θ成正比6.某种木材做成的长方体物块静止在水池(水域面积很宽)中时，恰好有一半没入水中，如图甲所示，物块在水中所受浮力F随着没入水中的深度h的图象如图丙所示。
陕西省安康市2019-2020学年第一次高考模拟考试数学试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（ ）A ．2-3B ．3-2C ．52D ．25【答案】C 【解析】 【分析】根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案.【详解】由题意，3,15a n ==， 第1次循环，2,23a n =-=，满足判断条件；第2次循环，5,32a n ==，满足判断条件；第3次循环，3,45a n ==，满足判断条件；L L可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =. 故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.12PF PF +=（ ）A ．4B ．8C ．D ．【答案】B 【解析】∵12F F =∵122F F c ==∴c =∵222c a b =-，24b = ∴4a =∴1228PF PF a +== 故选B点睛：本题主要考查利用椭圆的简单性质及椭圆的定义. 求解与椭圆性质有关的问题时要结合图形进行分析，既使不画出图形，思考时也要联想到图形，当涉及顶点、焦点、长轴、短轴等椭圆的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系. 3．已知α满足1sin 3α=，则cos cos 44ππαα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭（ ） A ．718B ．79C ．718-D ．79-【答案】A 【解析】 【分析】利用两角和与差的余弦公式展开计算可得结果. 【详解】1sin 3α=Q ，cos cos cos cos sin sin cos cos sin sin 444444ππππππαααααα⎛⎫⎛⎫⎛⎫⎛⎫∴+-=-+ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭()()22211cos cos cos sin 12sin 222222ααααααα⎛⎫⎛⎫=-+=-=- ⎪⎪ ⎪⎪⎝⎭⎝⎭2117122318⎡⎤⎛⎫=-⨯=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.本题考查三角求值，涉及两角和与差的余弦公式的应用，考查计算能力，属于基础题.4．已知等差数列{}n a 的公差为-2，前n 项和为n S ，若2a ，3a ，4a 为某三角形的三边长，且该三角形有一个内角为120︒，则n S 的最大值为（ ） A ．5 B ．11 C ．20 D ．25【答案】D 【解析】 【分析】由公差d=-2可知数列单调递减，再由余弦定理结合通项可求得首项，即可求出前n 项和，从而得到最值. 【详解】等差数列{}n a 的公差为-2，可知数列单调递减，则2a ，3a ，4a 中2a 最大，4a 最小， 又2a ，3a ，4a 为三角形的三边长，且最大内角为120︒，由余弦定理得22223434a a a a a =++，设首项为1a ，即()()()()()222111112a 4a 6a 4a 60a -=-+-+--=得()()11490a a --=，所以14a =或19a =，又41a 60a ，=->即1a 6>,14a =舍去，19a =故，d=-2 前n 项和()()()219n 25252n n n S n -=+⨯-=--+.故n S 的最大值为525S =. 故选：D 【点睛】本题考查等差数列的通项公式和前n 项和公式的应用，考查求前n 项和的最值问题，同时还考查了余弦定理的应用.5．已知抛物线2:2(0)C y px p =>的焦点为F ，过点F 的直线l 与抛物线C 交于A ，B 两点（设点A 位于第一象限），过点A ，B 分别作抛物线C 的准线的垂线，垂足分别为点1A ，1B ，抛物线C 的准线交x 轴于点K ，若11||2||A KB K =，则直线l 的斜率为 A ．1 B． C．D【答案】C 【解析】根据抛物线定义，可得1||||AF AA =，1||||BF BB =， 又11AA FK BB ∥∥，所以11||||2||||A K AF B K BF ==，所以1111||||2||||A K AAB K BB ==， 设1||(0)BB m m =>，则1||2AA m =，则111||||21cos cos ||23AA BB m m AFx BAA AB m m --∠=∠===+，所以sin AFx ∠=，所以直线l的斜率tan k AFx =∠=C ． 6．已知P 为圆C ：22(5)36x y -+=上任意一点，(5,0)A -，若线段PA 的垂直平分线交直线PC 于点Q ，则Q 点的轨迹方程为( )A ．221916x y +=B ．221916x y -=C ．221916x y -=（0x <）D ．221916x y -=（0x >）【答案】B 【解析】 【分析】如图所示：连接QA ，根据垂直平分线知QA QP =，610QC QA -=<，故轨迹为双曲线，计算得到答案. 【详解】如图所示：连接QA ，根据垂直平分线知QA QP =，故610QC QA QC QP PC -=-==<，故轨迹为双曲线，26a =，3a =，5c =，故4b =，故轨迹方程为221916x y -=.故选：B .【点睛】本题考查了轨迹方程，确定轨迹方程为双曲线是解题的关键.7．已知实数x，y满足约束条件202201x yx yx+-≤⎧⎪--≤⎨⎪≥⎩，则目标函数21yzx-=+的最小值为A．23-B．54-C．43-D．12-【答案】B【解析】【分析】作出不等式组对应的平面区域，目标函数21yzx-=+的几何意义为动点(),M x y到定点()1,2D-的斜率，利用数形结合即可得到z的最小值．【详解】当M 位于11,2A ⎛⎫- ⎪⎝⎭时，此时DA 的斜率最小，此时1252114min z --==-+． 故选B ． 【点睛】本题主要考查线性规划的应用以及两点之间的斜率公式的计算，利用z 的几何意义，通过数形结合是解决本题的关键． 8．已知(),A A Ax y 是圆心为坐标原点O ，半径为1的圆上的任意一点，将射线OA 绕点O 逆时针旋转23π到OB 交圆于点(),B B B x y ，则2AB yy +的最大值为（ ）A ．3B ．2C D 【答案】C 【解析】 【分析】设射线OA 与x 轴正向所成的角为α，由三角函数的定义得sin A y α=，2sin()3B y πα=+，2A B y y +=3sin 2αα+，利用辅助角公式计算即可.【详解】设射线OA 与x 轴正向所成的角为α，由已知，cos ,sin A A x y αα==，22cos(),sin()33B B x y ππαα=+=+，所以2A B y y +=2sin α+2sin()3πα+=12sin sin cos 22ααα-+=3sin )226πααα+=+≤，当3πα=时，取得等号.故选：C. 【点睛】本题考查正弦型函数的最值问题，涉及到三角函数的定义、辅助角公式等知识，是一道容易题. 9．已知1F ，2F 是椭圆22221(0)x y C a b a b +=>>：的左、右焦点，过2F 的直线交椭圆于,P Q 两点.若2211||,||,||,||QF PF PF QF 依次构成等差数列，且1||PQ PF =，则椭圆C 的离心率为A ．23B ．34C ．5D【分析】 【详解】如图所示，设2211||,||,||,||QF PF PF QF 依次构成等差数列{}n a ，其公差为d.根据椭圆定义得12344a a a a a +++=，又123a a a +=，则1111111()(2)(3)4()2a a d a d a d aa a d a d++++++=⎧⎨++=+⎩，解得25d a =，12342468,,,5555a a a a a a a a ====.所以18||5QF a =，16||5PF a =，24||5PF a =，6||5PQ a =.在12PF F △和1PFQ V 中，由余弦定理得2222221246668()()(2)()()()55555cos 4666225555a a c a a a F PF a a a a +-+-∠==⋅⋅⋅⋅，整理解得105c e a ==.故选D ． 10．如图，在等腰梯形ABCD 中，//AB DC ，222AB DC AD ===，60DAB ∠=︒，E 为AB 的中点，将ADE ∆与BEC ∆分别沿ED 、EC 向上折起，使A 、B 重合为点F ，则三棱锥F DCE -的外接球的体积是（ ）A 6B 6C ．32π D ．23π 【答案】A 【解析】 【分析】由题意等腰梯形中的三个三角形都是等边三角形，折叠成的三棱锥是正四面体，易求得其外接球半径，得由题意等腰梯形中DA AE EB BC CD ====，又60DAB ∠=︒，∴AED ∆，BCE ∆是靠边三角形，从而可得DE CE CD ==，∴折叠后三棱锥F DEC -是棱长为1的正四面体， 设M 是DCE ∆的中心，则FM ⊥平面DCE ，23313DM =⨯⨯=，226FM FD DM =-=， F DCE -外接球球心O 必在高FM 上，设外接球半径为R ，即OF OD R ==，∴22263()()R R =-+，解得6R =， 球体积为334466()3348V R πππ==⨯=． 故选：A ．【点睛】本题考查求球的体积，解题关键是由已知条件确定折叠成的三棱锥是正四面体． 11．若1tan 2α=，则cos2=α( ) A ．45-B ．35- C ．45D ．35【答案】D 【解析】 【分析】直接利用二倍角余弦公式与弦化切即可得到结果． 【详解】 ∵1tan 2α=， ∴22222211cos sin 1tan 34cos21cos sin 1tan 514ααααααα---====+++， 故选D能力和转化能力，属于基础题型． 12．已知三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若，，,AB AC ⊥112AA O =，则球的半径为( )A B ．C ．132D ．【答案】C 【解析】因为直三棱柱中，AB ＝3，AC ＝4，AA 1＝12，AB ⊥AC ，所以BC ＝5，且BC 为过底面ABC 的截面圆的直径．取BC 中点D ，则OD ⊥底面ABC ，则O 在侧面BCC 1B 1内，矩形BCC 1B 1的对角线长即为球直径，所以2R 13，即R ＝132二、填空题：本题共4小题，每小题5分，共20分。
陕西省安康市2019-2020学年高考数学第一次调研试卷一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
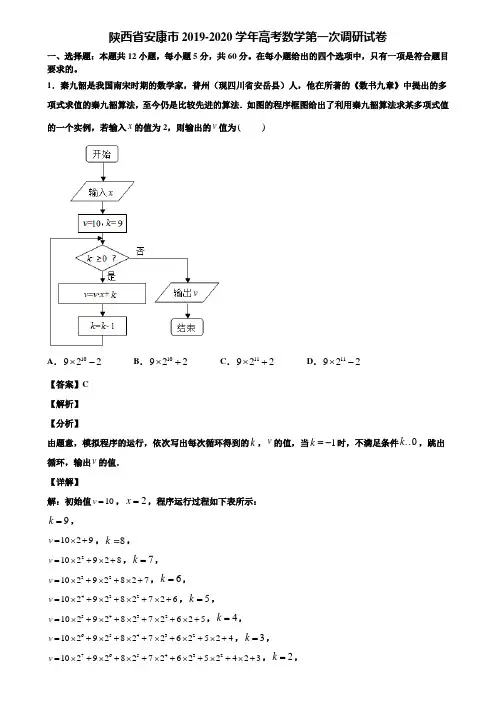
1．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x 的值为2，则输出的v 值为( )A ．10922⨯-B ．10922⨯+C ．11922⨯+D ．11922⨯-【答案】C 【解析】 【分析】由题意，模拟程序的运行，依次写出每次循环得到的k ，v 的值，当1k =-时，不满足条件0k …，跳出循环，输出v 的值． 【详解】解：初始值10v =，2x =，程序运行过程如下表所示：9k =，1029v =⨯+，8k=，2102928v =⨯+⨯+，7k =， 2310292827v =⨯+⨯+⨯+，6k =， 4321029282726v =⨯+⨯+⨯+⨯+，5k =， 4325102928272625v =⨯+⨯+⨯+⨯+⨯+，4k =， 6543210292827262524v =⨯+⨯+⨯+⨯+⨯+⨯+，3k =， 6574321029282726252423v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+，2k =，7654328102928272625242322v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+，1k =， 4987653210292827262524232221v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+，0k =，98765432101029282726252423222120v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+，1k =-，跳出循环，输出v 的值为其中98765432101029282726252423222120v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+① 10987651143221029282726252423222120v =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+②①—②得41711098653210212121212121212121212v -=-⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯ ()111021210212v --=-⨯+-11922v =⨯+．故选：C ． 【点睛】本题主要考查了循环结构的程序框图的应用，正确依次写出每次循环得到k ，v 的值是解题的关键，属于基础题．2．曲线24x y =在点()2,t 处的切线方程为（ ） A ．1y x =- B ．23y x =-C ．3y x =-+D ．25y x =-+【答案】A 【解析】 【分析】将点代入解析式确定参数值，结合导数的几何意义求得切线斜率，即可由点斜式求的切线方程. 【详解】曲线24x y =，即214y x =， 当2x =时，代入可得21124t =⨯=，所以切点坐标为()2,1，求得导函数可得12y x '=， 由导数几何意义可知1212k y ='=⨯=， 由点斜式可得切线方程为12y x -=-，即1y x =-， 故选：A. 【点睛】本题考查了导数的几何意义，在曲线上一点的切线方程求法，属于基础题.3．若复数()(1)2z i i =++（i 是虚数单位），则复数z 在复平面内对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A 【解析】 【分析】将z 整理成a bi +的形式，得到复数所对应的的点，从而可选出所在象限. 【详解】解：221()()2313z i i i i i =++=++=+，所以z 所对应的点为()1,3在第一象限.故选:A. 【点睛】本题考查了复数的乘法运算，考查了复数对应的坐标.易错点是误把2i 当成1进行计算.4．已知P 与Q 分别为函数260x y --=与函数21y x =+的图象上一点，则线段||PQ 的最小值为( )A ．65B ．CD ．6【答案】C 【解析】 【分析】利用导数法和两直线平行性质，将线段||PQ 的最小值转化成切点到直线距离. 【详解】已知P 与Q 分别为函数260x y --=与函数21y x =+的图象上一点， 可知抛物线21y x =+存在某条切线与直线260x y --=平行，则2k =，设抛物线21y x =+的切点为()200,1x x +，则由2y x '=可得022x =，01x ∴=，所以切点为(1,2)，则切点(1,2)到直线260x y --=的距离为线段||PQ 的最小值，则min ||5PQ ==. 故选：C. 【点睛】本题考查导数的几何意义的应用，以及点到直线的距离公式的应用，考查转化思想和计算能力. 5．设函数()()21ln 11f x x x=+-+，则使得()()1f x f >成立的x 的取值范围是（ ）． A ．()1,+∞B ．()(),11,-∞-+∞UC ．()1,1-D ．()()1,00,1-U【答案】B 【解析】 【分析】由奇偶性定义可判断出()f x 为偶函数，由单调性的性质可知()f x 在[)0,+∞上单调递增，由此知()f x 在(],0-∞上单调递减，从而将所求不等式化为1x >，解绝对值不等式求得结果. 【详解】由题意知：()f x 定义域为R ，()()()()()2211ln 1ln 111f x x x f x xx -=+--=+-=++-Q ，()f x ∴为偶函数， 当0x ≥时，()()21ln 11f x x x =+-+， ()ln 1y x =+Q 在[)0,+∞上单调递增，211y x=+在[)0,+∞上单调递减， ()f x ∴在[)0,+∞上单调递增，则()f x 在(],0-∞上单调递减，由()()1f x f >得：1x >，解得：1x <-或1x >，x \的取值范围为()(),11,-∞-+∞U .故选：B . 【点睛】本题考查利用函数的单调性和奇偶性求解函数不等式的问题；奇偶性的作用是能够确定对称区间的单调性，单调性的作用是能够将函数值的大小关系转化为自变量的大小关系，进而化简不等式.6．著名的斐波那契数列{}n a ：1，1，2，3，5，8，…，满足121a a ==，21n n n a a a ++=+，*N n ∈，若2020211n n k a a -==∑，则k =( )A ．2020B ．4038C ．4039D ．4040【答案】D 【解析】 【分析】计算134a a a +=，代入等式，根据21n n n a a a ++=+化简得到答案. 【详解】11a =，32a =，43a =，故134a a a +=，202021134039457403967403940401............n n aa a a a a a a a a a a -==+++=++++=+++==∑，故4040k =. 故选：D . 【点睛】本题考查了斐波那契数列，意在考查学生的计算能力和应用能力.7．过双曲线2222:1(0,0)x y C a b a b-=>>的右焦点F 作双曲线C 的一条弦AB ，且0FA FB +=u u u v u u u v ，若以AB为直径的圆经过双曲线C 的左顶点，则双曲线C 的离心率为（ ） ABC ．2D【答案】C 【解析】 【分析】由0FA FB +=u u u r u u u r 得F 是弦AB 的中点.进而得AB 垂直于x 轴，得2b ac a=+，再结合,,a b c 关系求解即可【详解】因为0FA FB +=u u u r u u u r，所以F 是弦AB 的中点.且AB 垂直于x 轴.因为以AB 为直径的圆经过双曲线C 的左顶点，所以2b a c a =+，即22c a a c a-=+，则c a a -=，故2c e a ==.故选：C 【点睛】本题是对双曲线的渐近线以及离心率的综合考查，是考查基本知识，属于基础题． 8．设正项等差数列{}n a 的前n 项和为n S ，且满足6322S S -=，则2823a a 的最小值为A ．8B ．16C ．24D ．36【答案】B 【解析】 【分析】 【详解】方法一：由题意得636332()2S S S S S -=--=，根据等差数列的性质，得96633,,S S S S S --成等差数列，设3(0)S x x =>，则632S S x -=+，964S S x -=+，则222288789962212333(3)()()=3a a a a a S S a a a a a S ++-==++2(4)x x+=168816x x =++≥=，当且仅当4x =时等号成立，从而2823a a 的最小值为16，故选B ．方法二：设正项等差数列{}n a 的公差为d ，由等差数列的前n 项和公式及6322S S -=，化简可得11653262(3)222a d a d ⨯⨯+-+=，即29d =，则2222822222243()33(6)163383a a a d a a a a a ++===++≥816=，当且仅当221633a a =，即243a =时等号成立，从而2823a a 的最小值为16，故选B ．9．设集合{}2320M x x x =++>，集合1{|()4}2xN x =≤ ，则 M N ⋃=（ ）A ．{}2x x ≥- B ．{}1x x >-C ．{}2x x ≤-D ．R【答案】D 【解析】试题分析：由题{}{}2320|21M x x x x x x =++=--或，{}2111|()4|()|2222x x N x x N x x -⎧⎫⎪⎪⎧⎫⎛⎫=≤=≤==≥-⎨⎬⎨⎬ ⎪⎩⎭⎝⎭⎪⎪⎩⎭，M N R ∴⋃=，选D考点：集合的运算10．设正项等比数列{}n a 的前n 项和为n S ，若23S =，3412a a +=，则公比q =（ ） A ．4± B ．4C ．2±D ．2【答案】D 【解析】 【分析】由23S =得123a a +=，又23412()12a a a a q +=+=，两式相除即可解出q ．【详解】解：由23S =得123a a +=，又23412()12a a a a q +=+=，∴24q =，∴2q =-，或2q =，又正项等比数列{}n a 得0q >， ∴2q =， 故选：D ． 【点睛】本题主要考查等比数列的性质的应用，属于基础题．11．已知函数()f x 满足()()11f x f x -=+，当1x ≥时，()2f x x x=-，则()}{21x f x +>=（ ）A ．{3x x <-或}0x > B ．{0x x <或}2x > C ．{2x x <-或}0x > D ．{2x x <或}4x >【答案】C 【解析】 【分析】简单判断可知函数关于1x =对称，然后根据函数()2f x x x =-的单调性，并计算210x xx ⎧-=⎪⎨⎪≥⎩，结合对称性，可得结果. 【详解】由()()11f x f x -=+， 可知函数()f x 关于1x =对称 当1x ≥时，()2f x x x=-， 可知()2f x x x=-在[)1,+∞单调递增 则2120x x xx ⎧-=⎪⇒=⎨⎪≥⎩ 又函数()f x 关于1x =对称，所以()01f = 且()f x 在(),1-∞单调递减，所以20x +<或22x +>，故2x <-或0x > 所以()}{21x f x +>={2x x <-或}0x > 故选：C 【点睛】本题考查函数的对称性以及单调性求解不等式，抽象函数给出式子的意义，比如：()()11f x f x -=+，()()110f x f x -++=，考验分析能力，属中档题.12．在平面直角坐标系中，若不等式组44021005220x y x y x y -+≤⎧⎪+-≤⎨⎪-+≥⎩所表示的平面区域内存在点()00,x y ，使不等式0010x my ++≤成立，则实数m 的取值范围为（ ）A ．5(,]2-∞- B ．1(,]2-∞-C ．[4,)+∞D ．(,4]-∞-【答案】B 【解析】 【分析】依据线性约束条件画出可行域，目标函数0010x my ++≤恒过()1,0D -，再分别讨论m 的正负进一步确定目标函数与可行域的基本关系，即可求解 【详解】作出不等式对应的平面区域，如图所示：其中()2,6A ，直线10x my ++=过定点()1,0D -，当0m =时，不等式10x +≤表示直线10x +=及其左边的区域，不满足题意； 当0m >时，直线10x my ++=的斜率10m-<， 不等式10x my ++≤表示直线10x my ++=下方的区域，不满足题意； 当0m <时，直线10x my ++=的斜率10m->， 不等式10x my ++≤表示直线10x my ++=上方的区域， 要使不等式组所表示的平面区域内存在点()00,x y ，使不等式0010x my ++≤成立，只需直线10x my ++=的斜率12AD k m -≤=，解得12m ≤-. 综上可得实数m 的取值范围为1(,]2-∞-， 故选：B. 【点睛】本题考查由目标函数有解求解参数取值范围问题，分类讨论与数形结合思想，属于中档题 二、填空题：本题共4小题，每小题5分，共20分。
陕西省安康市2019-2020学年高考第一次适应性考试数学试题一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设实数x 、y 满足约束条件1024x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则23z x y =+的最小值为（ ）A ．2B ．24C ．16D ．14【答案】D 【解析】 【分析】做出满足条件的可行域，根据图形即可求解. 【详解】做出满足1024x y x y x +≤⎧⎪-≤⎨⎪≥⎩的可行域，如下图阴影部分，根据图象，当目标函数23z x y =+过点A 时，取得最小值，由42x x y =⎧⎨-=⎩，解得42x y =⎧⎨=⎩，即(4,2)A ， 所以23z x y =+的最小值为14. 故选：D.【点睛】本题考查二元一次不等式组表示平面区域，利用数形结合求线性目标函数的最值，属于基础题. 2．已知函数2()sin 3cos444f x x x x πππ=，则(1)(2)...(2020)f f f +++的值等于（ ）A ．2018B ．1009C ．1010D ．2020【解析】 【分析】首先，根据二倍角公式和辅助角公式化简函数解析式，根据所求函数的周期性，得到其周期为4，然后借助于三角函数的周期性确定其值即可． 【详解】 解：2()sincos444f x x x x πππ=．1(1cos )222x x ππ=- 1sin()262x ππ=-++，1()sin()262f x x ππ∴=-++，()f x ∴的周期为242T ππ==，()1f ，()21f =， ()3f =，()40f =， ()()()()12342f f f f +++=． ()()()122020f f f ∴+++L ()()()()5051234f f f f =⨯+++⎡⎤⎣⎦5052=⨯1010=．故选：C 【点睛】本题重点考查了三角函数的图象与性质、三角恒等变换等知识，掌握辅助角公式化简函数解析式是解题的关键，属于中档题．3．在一个数列中，如果*n N ∀∈，都有12n n n a a a k ++=（k 为常数），那么这个数列叫做等积数列，k 叫做这个数列的公积.已知数列{}n a 是等积数列，且11a =，22a =，公积为8，则122020a a a ++⋅⋅⋅+=（ ）A ．4711B ．4712C ．4713D ．4715【答案】B 【解析】 【分析】计算出3a 的值，推导出()3n n a a n N *+=∈，再由202036731=⨯+，结合数列的周期性可求得数列{}na 的前2020项和.由题意可知128n n n a a a ++=，则对任意的n *∈N ，0n a ≠，则1238a a a =，31284a a a ∴==， 由128n n n a a a ++=，得1238n n n a a a +++=，12123n n n n n n a a a a a a +++++∴=，3n n a a +∴=，202036731=⨯+Q ，因此，()1220201231673673714712a a a a a a a ++⋅⋅⋅+=+++=⨯+=.故选：B. 【点睛】本题考查数列求和，考查了数列的新定义，推导出数列的周期性是解答的关键，考查推理能力与计算能力，属于中等题.4．定义域为R 的偶函数()f x 满足任意x ∈R ，有(2)()(1)f x f x f +=-，且当[2,3]x ∈时，2()21218f x x x =-+-.若函数()log (1)a y f x x =-+至少有三个零点，则a 的取值范围是（ ）A．0,2⎛ ⎝⎭B．0,3⎛ ⎝⎭ C．0,5⎛ ⎝⎭ D．0,6⎛ ⎝⎭【答案】B 【解析】 【分析】由题意可得()f x 的周期为2，当[2,3]x ∈时，2()21218f x x x =-+-，令()log (1)a g x x =+，则()f x 的图像和()g x 的图像至少有3个交点，画出图像，数形结合，根据(2)(2)g f >，求得a 的取值范围. 【详解】()f x 是定义域为R 的偶函数，满足任意x ∈R ，(2)()(1)f x f x f +=-，令1,(1)(1)(1)x f f f =-=--，又(1)(1),(1))(2)(0,f f x f x f f -=∴+==，()f x ∴为周期为2的偶函数，当[2,3]x ∈时，22()212182(3)f x x x x =-+-=--，当2[0,1],2[2,3],()(2)2(1)x x f x f x x ∈+∈=+=--， 当2[1,0],[0,1],()()2(1)x x f x f x x ∈--∈=-=-+， 作出(),()f x g x 图像，如下图所示：函数()log (1)a y f x x =-+至少有三个零点， 则()f x 的图像和()g x 的图像至少有3个交点，()0f x ≤Q ，若1a >，()f x 的图像和()g x 的图像只有1个交点，不合题意，所以01a <<，()f x 的图像和()g x 的图像至少有3个交点， 则有(2)(2)g f >，即log (21)(2)2,log 32a a f +>=-∴>-，221133,,01,03a a a a ∴><<<∴<<Q . 故选:B.【点睛】本题考查函数周期性及其应用，解题过程中用到了数形结合方法，这也是高考常考的热点问题，属于中档题.5．已知等比数列{}n a 满足13a =，13521a a a ++=，则357a a a ++=（ ） A ．21 B ．42 C ．63 D ．84【答案】B 【解析】由a 1+a 3+a 5=21得242421(1)21172a q q q q q ++=∴++=∴=∴ a 3+a 5+a 7=2135()22142q a a a ++=⨯=，选B.6．《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍.其中记载有求“囷盖”的术：“置如其周，令相承也.又以高乘之，三十六成一”.该术相当于给出了由圆锥的底面周长L 与高h ，计算其体积2136V L h ≈的近似公式.它实际上是将圆锥体积公式中的圆周率近似取为3.那么近似公式23112V L h ≈相当于将圆锥体积公式中的圆周率近似取为（ ） A ．227B ．15750C ．289D ．337115【答案】C【分析】将圆锥的体积用两种方式表达，即213V r h π==23(2)112r h π，解出π即可. 【详解】设圆锥底面圆的半径为r ，则213V r h π=，又2233(2)112112V L h r h π≈=， 故23(2)112r h π213r h π≈，所以，11228369π≈=. 故选：C. 【点睛】本题利用古代数学问题考查圆锥体积计算的实际应用，考查学生的运算求解能力、创新能力. 7．已知函数3()1f x x ax =--，以下结论正确的个数为（ ） ①当0a =时，函数()f x 的图象的对称中心为(0,1)-； ②当3a ≥时，函数()f x 在(–1,1)上为单调递减函数； ③若函数()f x 在(–1,1)上不单调，则0<<3a ； ④当12a =时，()f x 在[–4,5]上的最大值为1． A ．1 B ．2 C ．3 D ．4【答案】C 【解析】 【分析】逐一分析选项，①根据函数3y x =的对称中心判断；②利用导数判断函数的单调性；③先求函数的导数，若满足条件，则极值点必在区间()1,1-；④利用导数求函数在给定区间的最值. 【详解】①3y x =为奇函数，其图象的对称中心为原点，根据平移知识，函数()f x 的图象的对称中心为(0,1)-，正确．②由题意知2()3f x x a '=-．因为当–11x <<时，233x <，又3a ≥，所以()0f x '<在(1,1)-上恒成立，所以函数()f x 在(1,1)-上为单调递减函数，正确． ③由题意知2()3f x x a '=-，当0a ≤时，()0f x '≥，此时()f x 在(–),∞+∞上为增函数，不合题意，故0a >．令()0f x '=，解得x =．因为()f x 在(1,1)-上不单调，所以()0f x '=在(1,1)-上有解，需013<<，解得0<<3a ，正确． ④令2()3120f x x '=-=，得2x =±．根据函数的单调性，()f x 在[–4,5]上的最大值只可能为(2)f -或(5)f ．因为(2)15f -=，(5)64f =，所以最大值为64，结论错误． 故选：C 【点睛】本题考查利用导数研究函数的单调性，极值，最值，意在考查基本的判断方法，属于基础题型.8．有一圆柱状有盖铁皮桶（铁皮厚度忽略不计），底面直径为20cm ，高度为100cm ，现往里面装直径为10cm 的球，在能盖住盖子的情况下，最多能装（ ）2.236≈≈≈） A ．22个 B ．24个C ．26个D ．28个【答案】C 【解析】 【分析】计算球心连线形成的正四面体相对棱的距离为，得到最上层球面上的点距离桶底最远为)()101n +-cm ，得到不等式)101100n +-≤，计算得到答案.【详解】由题意，若要装更多的球，需要让球和铁皮桶侧面相切，且相邻四个球两两相切， 这样，相邻的四个球的球心连线构成棱长为10cm 的正面体，易求正四面体相对棱的距离为，每装两个球称为“一层”，这样装n 层球，则最上层球面上的点距离桶底最远为)()101n +-cm ，若想要盖上盖子，则需要满足)101100n +-≤，解得113.726n ≤+≈， 所以最多可以装13层球，即最多可以装26个球． 故选：C 【点睛】本题考查了圆柱和球的综合问题，意在考查学生的空间想象能力和计算能力.9．函数sin ln ||2y x x π⎛⎫=-⋅ ⎪⎝⎭图像可能是（ ）A ．B ．C ．D ．【答案】D 【解析】 【分析】先判断函数的奇偶性可排除选项A,C ，当0x +→时，可分析函数值为正，即可判断选项. 【详解】sin ln ||cos ln ||2y x x x x π⎛⎫=-⋅=- ⎪⎝⎭Q ,cos()ln ||cos ln ||x x x x ∴---=-,即函数为偶函数， 故排除选项A,C ，当正数x 越来越小，趋近于0时，cos 0,ln ||0x x -<<，所以函数sin ln ||02y x x π⎛⎫=-⋅> ⎪⎝⎭，故排除选项B,故选：D 【点睛】本题主要考查了函数的奇偶性，识别函数的图象，属于中档题.10．过圆224x y +=外一点(4,1)M -引圆的两条切线，则经过两切点的直线方程是（ ）． A ．440x y --= B ．440x y +-= C ．440x y ++= D ．440x y -+=【答案】A 【解析】过圆222x y r +=外一点(,)m n ，11．已知集合{}2(,)|A x y y x ==，{}22(,)|1B x y xy =+=，则A B I 的真子集个数为（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】 【分析】求出A B I 的元素，再确定其真子集个数． 【详解】由2221y x x y ⎧=⎨+=⎩，解得12x y ⎧⎪=⎪⎨⎪=⎪⎩或12x y ⎧⎪=⎪⎨⎪=⎪⎩，∴A B I 中有两个元素，因此它的真子集有3个． 故选：C. 【点睛】本题考查集合的子集个数问题，解题时可先确定交集中集合的元素个数，解题关键是对集合元素的认识，本题中集合,A B 都是曲线上的点集．12．将3个黑球3个白球和1个红球排成一排，各小球除了颜色以外其他属性均相同，则相同颜色的小球不相邻的排法共有（ ） A ．14种 B ．15种C ．16种D ．18种【答案】D 【解析】 【分析】采取分类计数和分步计数相结合的方法，分两种情况具体讨论，一种是黑白依次相间，一种是开始仅有两个相同颜色的排在一起 【详解】首先将黑球和白球排列好，再插入红球.情况1：黑球和白球按照黑白相间排列（“黑白黑白黑白”或“白黑白黑白黑”），此时将红球插入6个球组成的7个空中即可，因此共有2×7=14种； 情况2：黑球或白球中仅有两个相同颜色的排在一起（“黑白白黑白黑”、“黑白黑白白黑”、“白黑黑白黑白”“白黑白黑黑白”），此时红球只能插入两个相同颜色的球之中，共4种. 综上所述，共有14+4=18种. 故选：D 【点睛】本题考查排列组合公式的具体应用，插空法的应用，属于基础题 二、填空题：本题共4小题，每小题5分，共20分。
陕西省安康市2019-2020学年高三上学期第一次调研化学试卷一、单选题（本大题共20小题，共50.0分）1.中华语言博大精深，下列词语中，其包含物理变化的是()A. 蜡炬成灰B. 曾青得铁C. 百炼成钢D. 大浪淘沙2.下列有关说法正确的是()A. 容量瓶使用前必须干燥，否则将引起误差B. 蒸馏实验结束后，先停止通冷凝水，再停止加热C. 含硫酸的废液倒入水槽，用水冲入下水道D. 不慎将酒精灯打翻在桌上失火时，立即用湿抹布盖灭3.在实验室进行下列实验，括号内的实验仪器或试剂都能用得上的是()A. 配制100g20%的氢氧化钠溶液(烧杯、100mL容量瓶、胶头滴管)B. 钠的焰色反应(铂丝、硫酸钠溶液、稀盐酸)C. 从碘水中提取碘(蒸发皿、酒精灯、玻璃棒)D. 除去水中的Cl−(铁架台、玻璃棒、漏斗)4.同温同压下，等质量的SO2和CO2相比较，下列叙述中正确的是()A. 体积比为16：11B. 分子数目比为16：11C. 密度比为16：11D. 物质的量比为16：115.下列关于0.2mol·L−1K2SO4溶液的正确说法是()A. 该溶液中所含K+、SO42−总数为0.6N A B. 500mL该溶液中含有0.1N A个K+C. 任意体积的该溶液中，K+浓度均是0.4mol·L−1 D. 2L该溶液中SO42−浓度是0.4mol·L−16.下列关于化学用语的表示正确的是()A. 质子数为8、质量数为17的原子： 817ClB. NH4Cl的电子式：C. 氯离子的结构示意图：D. 对硝基甲苯的结构简式：7.下列离子方程式正确的是()A. 二氧化锰和浓盐酸反应：MnO 2+4HCl(浓) △ ̲̲̲̲̲̲ Mn 2++2Cl 2↑+2H 2OB. 稀盐酸和硅酸钠溶液反应：SiO 32−+2H +=H 2SiO 3↓ C. 碳酸钙和稀盐酸反应：CO 32−+2H +=CO 2↑+H 2OD. 铜和氯化铁溶液反应：Fe 3++Cu =Fe 2++Cu 2+8. A 、B 、C 分别是三种常见单质；D 、E 、F 则是常见的三种氧化物，且有如图所示转化关系，下列说法错误的是( )A. B 可能是金属B. A 、B 、C 中肯定有O 2C. D 中一定含有A 元素D. D 、E 组成元素不可能完全相同9. 下列实验能达到实验目的的是( )A. 用图①装置制备Fe(OH)2并能较长时间观察其颜色B. 用图②装置探究温度对平衡移动的影响C. 用图③装置验证铁发生析氢腐蚀D. 用图④装置测定反应速率10. 下列有关实验操作，现象和解释或结论都正确的是( )选项 实验操作现象解释或结论A向某溶液中滴加双氧水后再加入KSCN 溶液溶液呈红色 溶液中一定含有Fe 2+ B 向饱和Na 2CO 3 溶液中通入足量CO 2 溶液变浑浊析出了NaHCO 3晶体 C两块相同的铝箔，其中一块用砂纸仔细打磨过，将两块铝箔分别在酒精灯上加热打磨过的铝箔先熔化 并滴落下来金属铝的熔点较低，打磨过的铝箔更易熔化D 加热盛有NaCl 和NH 4Cl 固体的试管试管底部固体减少，试管口有晶体凝结 可以用升华法分离NaCl 和 NH 4Cl 固体A. B. C. D. 11. 设N A 代表阿伏加德罗常数的值，下列说法正确的是( )A. 常温下，11.2L 甲烷含有的分子数为0.5N AB. 常温下，14g 乙烯含有的原子数为N AC. 1mol羟基含有的电子数为9N AD. 标准状况下，22.4L苯含有的分子数为N A12.关于氧化还原反应，下列说法正确的是()A. 被还原的物质是还原剂B. 氧化剂被还原，还原剂被氧化C. 失去电子，化合价降低的物质是还原剂D. 氧化剂失去电子，化合价升高13.镭是元素周期表中第七周期第ⅡA族元素，关于其叙述不正确的是()A. 镭的金属性比钙弱B. 单质能与水反应生成氢气C. 在化合物中呈+2价D. 碳酸镭难溶于水14.下列说法正确的是()A. 氢氧燃料电池放电时可以将化学能全部转化为电能B. 铜锌硫酸原电池(如图)工作时，电子从锌电极经电解液流向铜电极C. 将3mol H2与1mol N2混合于密闭容器中充分反应可生成2molNH3，转移电子数目为6N AD. 手机上用的锂离子电池充电时将电能转化为化学能15.某学习小组利用如图所示实验装置探究SO2的性质。
2019届安康市第二中学高三第一次模拟物理试卷一、单选题1.如图所示，质点A沿半径为R的圆周运动一周，回到出发点．在此过程中，路程和位移的大小分别是A. 2πR，2πRB. 0，2πRC. 2πR，0D. 0，0【答案】C【解析】【详解】质点A沿半径为R 的圆周运动一周，回到出发点。
在此过程中，路程等于圆周的周长，s=2πR．初位置和末位置重合，所以位移为0．故C正确，ABD错误。
故选C。
【点睛】解决本题的关键区分位移和路程，理解路程和位移的定义．路程等于物体运动轨迹的长度，位移的大小等于物体首末位置的距离．2.关于自由落体运动，下列说法正确的是（）A. 物体沿竖直方向下落的运动是自由落体运动B. 加速度为9.8m/s2的运动就是自由落体运动C. 物体只在重力作用下从静止开始下落的运动是自由落体运动D. 物体在重力作用下的运动就是自由落体运动【答案】C【解析】【详解】自由落体运动是物体只在重力作用下从静止开始下落的运动，它是一种初速度为零、加速度为g的竖直向下的匀加速直线运动，如果空气阻力的作用比较小、可以忽略不计，物体的下落也可以看作自由落体运动，所以C正确，ABD不正确。
故选：C3.关于质点，下列说法正确的是 ( )A. 如果物体的形状和大小对所研究的问题属于次要因素时，可把物体看做质点B. 只有体积很小的物体才能看做质点C. 凡轻小的物体，皆可看做质点D. 质点是理想化模型，实际上并不存在，所以引入质点概念没有多大意义【答案】A【解析】【详解】A. 如果物体的形状和大小对所研究的问题属于次要因素时，可把物体看做质点，所以A正确；B. 体积很小的物体，不一定能看成质点，如原子的体积很小，在研究原子内部结构的时候是不能看成质点的，所以B错误；C. 能看成质点的物体是可以忽略自身大小，不是以质量的大小来区分的，所以C错误；D. 质点是理想化模型，实际上并不存在，但引入质点方便于研究问题，所以D错误。
安康市2019～2020学年第一学期高三阶段性考试化学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3，考试结束后，将本试卷和答题卡一并交回。
4．本试卷可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl35.5 Ca 40 Fe 56 Ba 137一、选择题：本题共20小题，其中1~10题每小题2分，11~20题每小题3分，共50分。
在每小题给出的四个选项中，只有一项是最符合题目要求的。
1.近年来，我国大力弘扬中华优秀传统文化体现了中华民族的“文化自信”。
下列有关说法错误的是A. 成语“百炼成钢”、“蜡炬成灰”中均包含了化学变化B. 常温下，成语“金戈铁马”中的金属能溶于浓硝酸C. 谚语“雷雨肥庄稼”，其过程中包含了氧化还原反应D. 《荷塘月色》中“薄薄的青雾浮起在荷塘里”中的“青雾”属于胶体2.下列实验操作不是从实验安全角度考虑的是A. 稀释硫酸时将浓硫酸缓慢注入蒸馏水中，并不断搅拌B. 做有毒气体的实验时，对尾气进行适当处理C. 加热烧瓶里液体时，在烧瓶底部放几片碎瓷片D. 向试管里滴加液体时，滴管不能伸入试管内3.在实验室中完成下列各组实验时，需要使用到相应实验仪器的是A. 除去食盐中混有的少量碘：坩埚和分液漏斗B. 用酸性高锰酸钾溶液滴定Fe2+：烧杯、烧瓶C. 配制250mL1mol/L硫酸溶液：量筒、250mL容量瓶D. 检验亚硫酸钠是否发生变质：漏斗、酒精灯4.同温同压下,等质量的SO2气体和SO3气体相比较,下列叙述中正确的是( )A. 密度比为4:5B. 物质的量之比为4:5C. 体积比为1:1D. 原子数之比为3:45.下列表述正确的是A. 22.4LHCl 溶于水制得1L 盐酸时，其浓度为1 mol •L -1B. 1L0.3mol •L -1的CuCl 2溶液中含有Cu 2+和Cl -的总物质的量为0.9molC. 在K 2SO 4和NaCl 的中性混合水溶液中，如果c(Na +)=c(SO 42-)，则c(K +)=c(Cl -)D. 10℃时，100mLKCl 饱和溶液蒸发掉5g 水，冷却到10℃时，它仍为饱和溶液 6.下列说法中正确的是 A. 188O 2-离子结构示意图为B. 乙烯的结构简式为CH 2=CH 2C. NH 3溶于水后的溶液能导电，因此NH 3是电解质D. 正反应放热的可逆反应不需加热就能反应，升温，正反应速率降低 7.下列离子方程式符合题意且正确的是A. 磁性氧化铁溶于盐酸中：3232Fe O 6H 2Fe 3H O +++=+B. 在明矾溶液中加入过量2Ba(OH)溶液：322Al4OH AlO 2H O +--+=+C. 在盐酸中滴加少量23Na CO 溶液：2322CO 2H CO H O -++=↑+D. 用FeS 除去废水中的2Cu +：22S Cu CuS -++=↓8.已知A 是一种金属单质，B 显淡黄色，其转化关系如图所示，则下列说法错误的是A. A 与水反应可生成DB. B 常用于制作呼吸面具C. C 与澄清石灰水反应生成白色沉淀和DD. 将稀硫酸铝溶液逐滴滴入D 溶液中，开始时就会产生沉淀 9.下列实验操作能达到实验目的的是A. 除去Fe(OH)3胶体中的FeCl3杂质B. 证明浓硫酸与蔗糖反应生成SO 2C. 探究铁的析氢腐蚀D. 测定双氧水分解速率10.下列实验操作，现象和结论都正确的是选项操作现象结论A 用坩埚钳夹一块铝箔在酒精灯上灼烧铝箔熔化并滴落氧化铝的熔点较低B向亚硫酸钠溶液中滴加足量盐酸，将产生的气体通入品红溶液品红溶液褪色非金属性：Cl S>C将用砂纸除去保护膜镁片和铝片(大小、形状相同)，分别插入同浓度的稀硫酸中镁片表面产生气泡速率大于铝片还原性：Mg Al>D常温下，将两根大小相同的铁钉分别插入浓硝酸和稀硝酸中浓硝酸中无明显现象，稀硝酸中产生气泡稀硝酸的氧化性比浓硝酸强A. AB. BC. CD. D11.设A N 为阿伏加德罗常数的值。
