数字电路第四章习题

第四章 组合逻辑电路 作业 参考答案【题4-1】 分析图示组合逻辑电路，列出真值表，写出输出Y 1、Y 2与输入的逻辑函数式，说明整个电路所实现的逻辑功能（不是单个输出与输入的关系，而是把2个输出与3个输入综合起来看）。

解：该电路的逻辑功能为全加器，Y 1是和，Y 2是进位。

【题4-2】某汽车驾驶员培训班进行结业考试，有三名评判员，其中A 为主评判员，B 和C 为副评判员。

在评判时，按照少数服从多数的原则通过，但主评判员认为合格，方可通过。

请填写真值表，写出逻辑表达式，并用一片74LS00（内含四个2输入端与非门）或一片74LS02（内含四个2输入端或非门）这2种方法实现此评判规定。

解：设评判员评判合格为“1”，反之为“0”； 考试通过，F 为“1”，反之为“0”。

根据题意，列真值表如下。

据此可得：ABC12ABCC B A C B A C B A AC BC AB C B A ABC Y +++=+++++=)()(1AC BC AB Y ++=2ACAB AC AB F =+=CB AC B A F ++=+=)(FB CA FB CA【题4-3】设计一个“4输入1输出”的组合逻辑电路，实现“五舍六入”的功能：即当输入的四位8421BCD 码不大于5时，输出0；否则输出1。

要求： (1) 画出卡诺图、化简逻辑函数；(2) 用1片CD4001（内含四个2输入端或非门）实现该逻辑功能（标出管脚号）。

【题4-4】设计一个代码转换电路，输入为3位二进制代码、输出为3位格雷码（见下表），要求从CD4011、CD4001、CD4030中选用1个最合适的芯片实现逻辑功能。

解：CDAB Y 00X X 0X 011001X XXCA B A C A B A BC A Y +++=++=+=))((FB CA21313546121101000111XABC00011011YABC0010111ZABCAX =BA B A B A Y ⊕=+=CB C B C B Z ⊕=+=B CAYZX【题4-5】用一片74HC138（3-8译码器）辅以“4输入与非门”实现“1位全减”。

习题4.1写出图所示电路的逻辑表达式，并说明电路实现哪种逻辑门的功能。

习题4.1图解：B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能4.2分析图所示电路，写出输出函数F 。

习题4.2图解：[]B A B BB A F ⊕=⊕⊕⊕=)(4.3已知图示电路及输入A 、B 的波形，试画出相应的输出波形F ，不计门的延迟．图解：B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=4.4由与非门构成的某表决电路如图所示。

其中A 、B 、C 、D 表示4个人，L=1时表示决议通过。

（1） 试分析电路，说明决议通过的情况有几种。

（2） 分析A 、B 、C 、D 四个人中，谁的权利最大。

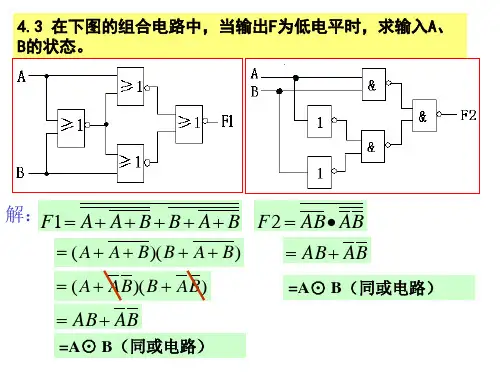
习题4.4图解：（1）ABD BC CD ABD BC CD L ++=••=B AC & && & D L B A =1 =1=1FF A B & &&& & F B A(3)4.5分析图所示逻辑电路，已知S 1﹑S 0为功能控制输入，A ﹑B 为输入信号，L 为输出，求电路所具有的功能。

习题4.5图解：（1）011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)4.6试分析图所示电路的逻辑功能。

习题4.6图解：（1）ABC C B A F )(++=10电路逻辑功能为：“判输入ABC 是否相同”电路。

4.7已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示，试写出F 的最简与或表达式。

习题4.7图解：（1）根据波形图得到真值表：C AB BC A C B A F ++=4.8、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ，要求用最简单的方法，实现的电路最简单。

1）用与非门实现。

2）用或非门实现。

3) 用与或非门实现。

数字电路与逻辑设计习题_4第四章组合逻辑电路剖析第四章组合逻辑电路一、选择题1．下列表达式中不存在竞争冒险的有。

A.Y=B +A BB.Y=A B+B CC.Y =A B C +ABD.Y =(A+B )A D 2．若在编码器中有50个编码对象，则要求输出二进制代码位数为位。

A.5B.6C.10D.503.一个16选一的数据选择器，其地址输入（选择控制输入）端有个。

A.1B.2C.4D.16 4.下列各函数等式中无冒险现象的函数式有。

A.B A AC C B F ++= B.B A BC C A F ++=C.B A B A BC C A F +++=D.C A B A BC B A AC C B F +++++=E.B A B A AC C B F +++= 5．函数C B AB C A F ++=，当变量的取值为时，将出现冒险现象。

A.B=C=1B.B =C=0C.A =1，C=0D.A =0，B=0 6．四选一数据选择器的数据输出Y 与数据输入X i 和地址码A i 之间的逻辑表达式为Y = 。

A.3X A A X A A X A A X A A 01201101001+++B.001X A AC.101X A AD.3X A A 017.一个8选一数据选择器的数据输入端有个。

A.1 B.2 C.3 D.4 E.8 8．在下列逻辑电路中，不是组合逻辑电路的有。

A.译码器B.编码器C.全加器 D.寄存器9．八路数据分配器，其地址输入端有个。

A.1B.2C.3D.4E.8 10．组合逻辑电路消除竞争冒险的方法有。

A. 修改逻辑设计B.在输出端接入滤波电容C.后级加缓冲电路D.屏蔽输入信号的尖峰干扰 11．101键盘的编码器输出位二进制代码。

A.2B.6C.7D.812．用三线-八线译码器74LS 138实现原码输出的8路数据分配器，应。

A.A ST =1，B ST =D ，C ST =0 B. A ST =1，B ST =D ，C ST =D C.A ST =1，BST =0，CST =D D.A ST =D ，BST =0，CST =013．以下电路中，加以适当辅助门电路，适于实现单输出组合逻辑电路。

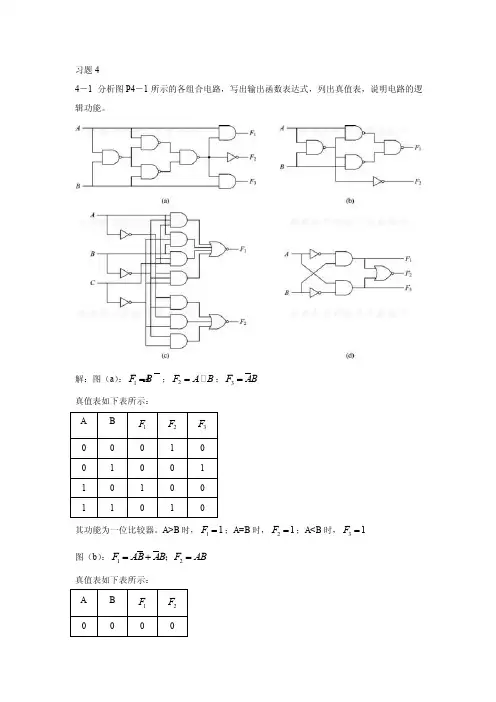
习题44－1 分析图P4－1所示的各组合电路，写出输出函数表达式，列出真值表，说明电路的逻辑功能。

解：图（a ）：1F A B =；2F A B = ；3F AB =真值表如下表所示：其功能为一位比较器。

A>B 时，11F =；A=B 时，21F =；A<B 时，31F = 图（b ）：12F AB AB F AB =+=； 真值表如下表所示：功能：一位半加器，1F 为本位和，2F 为进位。

图（c ）：1(0,35,6)(124,7)F M m==∑∏2(0,1,2,4)(3,5,6,7)F M m ==∑∏真值表如下表所示：功能：一位全加器，1F 为本位和，2F 为本位向高位的进位。

图（d ）：1F A B =；2F A B = ；3F AB =功能：为一位比较器，A<B 时，1F ＝1；A=B 时，2F ＝1；A>B 时，3F ＝14－2 分析图P4－2所示的组合电路，写出输出函数表达式，列出真值表，指出该电路完成的逻辑功能。

解：该电路的输出逻辑函数表达式为：100101102103F A A x A A x A A x A A x =+++因此该电路是一个四选一数据选择器，其真值表如下表所示：4－3 图P4－3是一个受M 控制的代码转换电路，当M ＝1时，完成4为二进制码至格雷码的转换；当M ＝0时，完成4为格雷码至二进制的转换。

试分别写出0Y ,1Y ,2Y ,3Y 的逻辑函数的表达式，并列出真值表，说明该电路的工作原理。

解：该电路的输入为3x 2x 1x 0x ，输出为3Y 2Y 1Y 0Y 。

真值表如下：由此可得：1M =当时，3323212101Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。

0M =当时，332321321210321010Y x Y x x Y x x x Y x Y x x x x Y x =⎧⎪=⊕⎪⎨=⊕⊕=⊕⎪⎪=⊕⊕⊕=⊕⎩ 完成格雷码至二进制的转换。

第四章 逻辑函数及其符号简化1.列出下述问题的真值表，并写出逻辑表达式：(1) 有A 、B 、C 三个输入信号，如果三个输入信号中出现奇数个1时，输出信号F=1，其余情况下，输出 F= 0.(2) 有A 、B 、C 三个输入信号，当三个输入信号不一致时，输出信号F=1，其余情况下，输出为0.(3) 列出输入三变量表决器的真值表•解：(1 )(1) F=AB+ A B1⑵ F= AB+ A C(3) F= (A+B+C) (A+B+ C ) (A+ B +C) (A+ B +C ) 解： (1) AB = 00 或 AB=11 时 F=1(2) ABC110 或 111 或 001,或 011 时 F=1 (3) ABC = 100 或 101 或 110 或 111 时 F=1 3. 用真值表证明下列等式.(1) A+BC = (A+B) (A+C)(2) A BC+A B C+AB C = BC ABC +AC ABC +AB ABC (3) A B + BC + AC =ABC+ A B C ⑷ AB+BC+AC=(A+B)(B+C)(A+C)A B C F0 0 0 00 01 10 10 10 11 0 1 0 0 11 01(2 )1 B 10 0 1 10 10 10 11 11 00 11 0 1 1 (3 )1 1 0 1 A 1B C F0 00 00 01 00 10 00 11 1 1 0 0 01 011F= A B C+ A B C +A B C +ABCF= (A+B+C) ( A + B +C )F= A BC+A B C+AB C +ABC ,F 的值为“ 12.对下列函数指出变量取哪些组值时(5) ABC+ A + B + C=1证：(1 )A B C A+BC(A+B)(A+C)0 0 0 0 00 0 1 0 00 1 0 0 00 1 1 1 11 0 0 1 11 0 1 1 11 1 0 1 1A B C ABC + ABC + ABC —BCABC + ACA B C + ABABC0 0 0 0 00 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 0(5 )A B C AB+ BC3 AC ABC + A"B"C—0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 0 01 0 0 0 01 0 1 0 01 1 0 0 01 1 1 1 1ABC AB+BC+AC (A+B)(B+C)(A+C)0 0 00 0 10 1 00 1 11 0 01 0 11 1 0 11ABC ABC + A + B + C0 0 0 10 0 1 10 1 0 10 1 1 11 0 0 11 0 1 1(5 )4. 直接写出下列函数的对偶式F'及反演式F的函数表达式(1) F=[A B(C+D)][B C D+B(C +D)](2) F= A BC + ( A +B C ) (A+C)⑶F= AB+ CD + BC + D + CE + D + E(4)F=C+AB?AB+ D解：(1) F'= [ A +B+CD]+[(B+ C+ D)?B+C D]]F = [A+ B + C D ]+[( B +C+D) ?( B +CD ]](2) F'= (A+ B + C)?[A?(B + C)AC]F = (A+ B<C)?[A?(B + C)+ A C]⑶F、=C?(A + B)+(A + B)?DF = C?(A + B) + (A + B)?D5. 若已知x+y = x+z，问y = z吗？为什么？解：y不一定等于z,因为若x=1时,若y=0,z=1,或y=1,z=0,则x+y = x+z = 1,逻辑或的特点，有一个为1则为1。

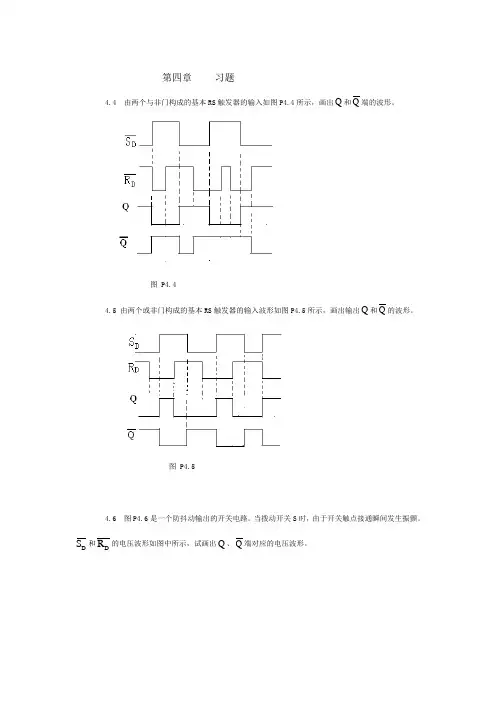
第四章习题4.4 由两个与非门构成的基本RS 触发器的输入如图P4.4所示，画出Q 和Q 端的波形。

图 P4.44.5 由两个或非门构成的基本RS 触发器的输入波形如图P4.5所示，画出输出Q 和Q 的波形。

图 P4.54.6 图P4.6是一个防抖动输出的开关电路。

当拨动开关S 时，由于开关触点接通瞬间发生振颤。

D S 和D R 的电压波形如图中所示，试画出Q 、Q 端对应的电压波形。

图P4.64.7 在同步RS触发器中，若CP、S、R的电压波形如图P4.7所示。

画出Q和Q端的波形。

设触发器的初始状态为Q=0。

图 P4.74.10 主从型JK触发器输入波形如图P4.10所示，画出输出端Q和Q的波形。

设触发器初始状态Q=0。

4.11 主从型JK 触发器组成图P4.11（a ）所示电路，输入波形如图P4.11（b ）所示，画出各触发器Q 端的波形。

（a ）解：AB J 1 ，先画出J 的波形，然后画Q.。

4.12 主从型RS 触发器的CP 、S 、R 、DR各输入的电压波形如图P4.12所示，画出端Q 和Q 端对应的电压波形。

图 P4.124.14 维持阻塞D触发器构成图P4.14所示的电路，输入波形如图P4.14（b）所示。

画出各触发器Q段的波形。

触发器的初态均为0。

（b）图 P4.144.16 上升沿触发的维持阻塞型D触发器74LS74组成图（a）所示电路，输入波形如图（b）所示，画出Q1和Q2的波形，设Q初态为0。

4.20 画出图P4.20电路在图中所示CP、R信号作用下Q1、Q2、Q3的输出电压波形，并说明DQ1、Q2、Q3输出信号的频率与CP信号频率之间的关系。

CP1/21/4QQQ频率的、1/8。

、和的频率分别是、132。

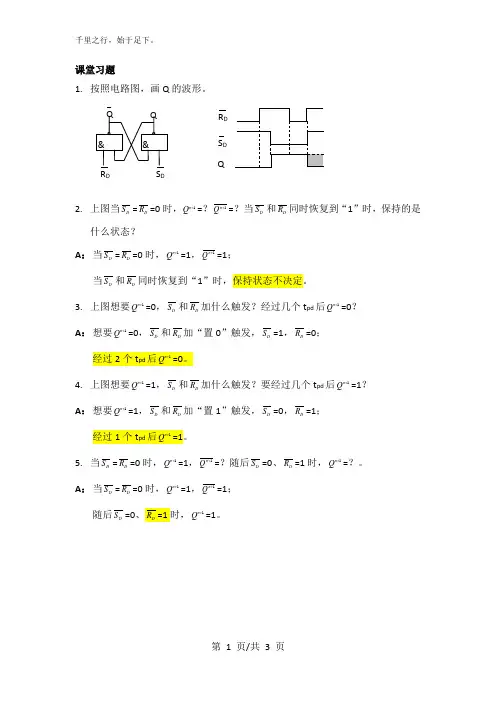
第 1 页/共 3 页1. 按照电路图，画Q 的波形。

2. 上图当D S =D R =0时，1n Q +=？1n Q +=？当D S 和D R 同时恢复到“1”时，保持的是什么状态？A ： 当D S =D R =0时，1n Q +=1，1n Q +=1；当D S 和D R 同时恢复到“1”时，保持状态不决定。

3. 上图想要1n Q +=0，D S 和D R 加什么触发？经过几个t pd 后1n Q +=0？A ： 想要1n Q +=0，D S 和D R 加“置0”触发，D S =1，D R =0；经过2个t pd 后1n Q +=0。

4. 上图想要1n Q +=1，D S 和D R 加什么触发？要经过几个t pd 后1n Q +=1？A ： 想要1n Q +=1，D S 和D R 加“置1”触发，D S =0，D R =1；经过1个t pd 后1n Q +=1。

5. 当D S =D R =0时，1n Q +=1，1n Q +=？随后D S =0、D R =1时，1n Q +=？。

A ： 当D S =D R =0时，1n Q +=1，1n Q +=1； 随后D S =01n Q +=1。

R D S D & &Q Q R D S D Q1. 有两个触发器如下，当CP 和D 有如下波形时，画Q 1、Q 2波形。

2. 用边沿D 触发器实现将CP 频率下降1/2和1/4的电路。

A ： 触发器特征方程为 1n n Q D Q +==每来一个时钟升高沿，Q 翻转一次，Q 1输出为2分频，Q 2输出为4分频。

T 1和T 2。

A ： T 2≥T su4. 当同步RS 触发器要想Q n+1=1时，RS 应加什么触发信号？写出特征方程。

求CP QQ T →=？A ： 应加R=0、S=1时，Q n+1=1特征方程 约束条件：0S R ⋅=CP QQ T →=3t pd 5. 当同步RS 触发器R=S=1时，1n Q +=？1n Q +=？随后R=S=0，问1n Q +=？倘若R=S=1之后R=1、S=0，1n Q +=？A ： R=S=1时，1n Q +=1，1n Q +=1随后R=S=0， 1n Q +=为不定状态 倘若R=S=1之后R=1、S=0，1n Q +=0D 1 Q 1 D 2 Q 2Q 2D Q 1 CP第3页/共3页。

数字电路第四章答案【篇一：数字电路答案第四章时序逻辑电路2】p=1，输入信号d被封锁，锁存器的输出状态保持不变；当锁存命令cp=0，锁存器输出q?d，q=d；当锁存命令cp出现上升沿，输入信号d被封锁。

根据上述分析，画出锁存器输出q及 q的波形如习题4.3图（c）所示。

习题4.4 习题图4.4是作用于某主从jk触发器cp、j、k、 rd及 sd 端的信号波形图，试绘出q端的波形图。

解：主从jk触发器的 rd、且为低有效。

只有当rd?sd?1 sd端为异步清零和复位端，时，在cp下降沿的作用下，j、k决定输出q状态的变化。

q端的波形如习题4.4图所示。

习题4.5 习题4.5图（a）是由一个主从jk触发器及三个非门构成的“冲息电路”，习题4.5图（b）是时钟cp的波形，假定触发器及各个门的平均延迟时间都是10ns，试绘出输出f的波形。

cpf cp100ns10nsq（a）f30ns10ns（b）（c）习题4.5图解：由习题4.5图（a）所示的电路连接可知：sd?j?k?1，rd?f。

当rd?1时，在cp下降沿的作用下，且经过10 ns，状态q发生翻转，再经过30ns，f发生状态的改变，f?q。

rd?0时，经过10ns，状态q=0。

根据上述对电路功能的分析，得到q和f的波形如习题4.5图（c）所示。

习题4.6 习题4.6图（a）是一个1检出电路，图（b）是cp及j端的输入波形图，试绘出 rd端及q端的波形图（注：触发器是主从触发器，分析时序逻辑图时，要注意cp=1时主触发器的存储作用）。

cpj（a）qd（c）cp j（b）习题图解：分析习题4.6图（a）的电路连接：sd?1,k?0,rd?cp?q；分段分析习题4.6图（b）所示cp及j端信号波形。

（1）cp=1时，设q端初态为0，则rd?1。

j信号出现一次1信号，即一次变化的干扰，且k=0，此时q端状态不会改变；（2）cp下降沿到来，q端状态变为1，rd?cp，此时cp=0，异步清零信号无效；（3）cp出现上升沿，产生异步清零信号，使q由1变为0，在很短的时间里 rd又恢复到1；（4）同理，在第2个cp=1期间，由于j信号出现1信号，在cp下降沿以及上升沿到来后，电路q端和 rd端的变化与（2）、（3）过程的分析相同，其波形如习题4.6图（c）所示。

思考题与习题4-1 触发器的主要性能是什么？它有哪几种结构形式？其触发方式有什么不同？触发器是一种存储电路，具有记忆功能。

在数字电路系统中起着重要作用。

依据不同的标准，触发器可以划分为多种不同类型。

从结构上来分，触发器分为基本触发器，时钟触发器，主从触发器以及边沿触发器。

基本触发器为异步（或直接）触发，时钟触发器为CP电平触发，主从和边沿触发器为边沿触发。

4-2 试分别写出RS触发器、JK触发器、D触发器、T触发器和T′触发器的状态转换表和特性方程。

（略）4-3 已知同步RS触发器的R、S、CP端的电压波形如图T4-3所示。

试画出Q、Q端的电压波形。

假定触发器的初始状态为0。

图T4-34-4 设边沿JK触发器的初始状态为0，CP、J、K信号如图T4-4所示，试画出触发器输出端Q、Q的波形。

图T4-44-5电路如图T4-5(a)所示，输入波形如图T4-5(b)所示，试画出该电路输出端G的波形，设触发器的初始状态为0。

图T5-24-6 试画出图T4-6所示波形加在以下两种触发器上时，触发器输出Q的波形：(1)下降沿触发的触发器(2)上升沿触发的触发器图T4-64-7 已知A、B为输入信号，试写出图T4-7所示各触发器的次态逻辑表达式。

图T4-7nn n n n n n n nn n )b (n )a (Q B Q B Q Q B AQ Q Q B AQ Q K Q J Q B A D Q ⋅=+=++=⋅+=+=⊕==++11 4-8 设图T4-8所示中各TTL 触发器的初始状态皆为0，试画出在CP 信号作用下各触发的输出端Q 1-Q 6的波形。

图T4-84-9 试对应画出图T4-9所示电路中Q 1、Q 2波形。

（初始状态均为0）图T4-94-10 一逻辑电路如图T4-10所示，试画出在CP 作用下3210Y Y Y Y 、、、的波形。

（CT74LS139为2线—4线译码器。

）图T4-104-11由边沿D触发器和边沿JK触发器组成图T4-11(a)所示的电路。

数字电子技术基础第四章习题及参考答案第四章习题1．分析图4-1中所示的同步时序逻辑电路，要求：（1）写出驱动方程、输出方程、状态方程；（2）画出状态转换图，并说出电路功能。

CPY图4-12．由D触发器组成的时序逻辑电路如图4-2所示，在图中所示的CP脉冲及D作用下，画出Q0、Q1的波形。

设触发器的初始状态为Q0=0，Q1=0。

D图4-23．试分析图4-3所示同步时序逻辑电路，要求：写出驱动方程、状态方程，列出状态真值表，画出状态图。

CP图4-34．一同步时序逻辑电路如图4-4所示，设各触发器的起始状态均为0态。

（1）作出电路的状态转换表；（2）画出电路的状态图；（3）画出CP作用下Q0、Q1、Q2的波形图；（4）说明电路的逻辑功能。

图4-45．试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0，并说明它的功能（假设初态Q0Q1=00）。

CPQ1Q0CP图4-56．分析如图4-6所示同步时序逻辑电路的功能，写出分析过程。

Y图4-67．分析图4-7所示电路的逻辑功能。

（1）写出驱动方程、状态方程；（2）作出状态转移表、状态转移图；（3）指出电路的逻辑功能，并说明能否自启动；（4）画出在时钟作用下的各触发器输出波形。

CP图4-78．时序逻辑电路分析。

电路如图4-8所示：（1）列出方程式、状态表；（2）画出状态图、时序图。

并说明电路的功能。

1C图4-89．试分析图4-9下面时序逻辑电路：（1）写出该电路的驱动方程，状态方程和输出方程；（2）画出Q1Q0的状态转换图；（3）根据状态图分析其功能；1B图4-910.分析如图4-10所示同步时序逻辑电路，具体要求：写出它的激励方程组、状态方程组和输出方程，画出状态图并描述功能。

1Z图4-1011．已知某同步时序逻辑电路如图4-11所示，试：（1）分析电路的状态转移图，并要求给出详细分析过程。

（2）电路逻辑功能是什么，能否自启动？（3）若计数脉冲f CP频率等于700Hz，从Q2端输出时的脉冲频率是多少?CP图4-1112．分析图4-12所示同步时序逻辑电路，写出它的激励方程组、状态方程组，并画出状态转换图。

数字电路第四章答案【篇一：数字电路答案第四章时序逻辑电路2】p=1，输入信号d被封锁，锁存器的输出状态保持不变；当锁存命令cp=0，锁存器输出q?d，q=d；当锁存命令cp出现上升沿，输入信号d被封锁。

根据上述分析，画出锁存器输出q及 q的波形如习题4.3图（c）所示。

习题4.4 习题图4.4是作用于某主从jk触发器cp、j、k、 rd及 sd 端的信号波形图，试绘出q端的波形图。

解：主从jk触发器的 rd、且为低有效。

只有当rd?sd?1 sd端为异步清零和复位端，时，在cp下降沿的作用下，j、k决定输出q状态的变化。

q端的波形如习题4.4图所示。

习题4.5 习题4.5图（a）是由一个主从jk触发器及三个非门构成的“冲息电路”，习题4.5图（b）是时钟cp的波形，假定触发器及各个门的平均延迟时间都是10ns，试绘出输出f的波形。

cpf cp100ns10nsq（a）f30ns10ns（b）（c）习题4.5图解：由习题4.5图（a）所示的电路连接可知：sd?j?k?1，rd?f。

当rd?1时，在cp下降沿的作用下，且经过10 ns，状态q发生翻转，再经过30ns，f发生状态的改变，f?q。

rd?0时，经过10ns，状态q=0。

根据上述对电路功能的分析，得到q和f的波形如习题4.5图（c）所示。

习题4.6 习题4.6图（a）是一个1检出电路，图（b）是cp及j端的输入波形图，试绘出 rd端及q端的波形图（注：触发器是主从触发器，分析时序逻辑图时，要注意cp=1时主触发器的存储作用）。

cpj（a）qd（c）cp j（b）习题图解：分析习题4.6图（a）的电路连接：sd?1,k?0,rd?cp?q；分段分析习题4.6图（b）所示cp及j端信号波形。

（1）cp=1时，设q端初态为0，则rd?1。

j信号出现一次1信号，即一次变化的干扰，且k=0，此时q端状态不会改变；（2）cp下降沿到来，q端状态变为1，rd?cp，此时cp=0，异步清零信号无效；（3）cp出现上升沿，产生异步清零信号，使q由1变为0，在很短的时间里 rd又恢复到1；（4）同理，在第2个cp=1期间，由于j信号出现1信号，在cp下降沿以及上升沿到来后，电路q端和 rd端的变化与（2）、（3）过程的分析相同，其波形如习题4.6图（c）所示。

数字电路第四章例题本文由cupidqiu贡献ppt文档可能在WAP端浏览体验不佳。

建议您优先选择TXT，或下载源文件到本机查看。

第四章例题信电学院马草原例1 分析下图所示电路的逻辑功能.解:为了方便写表达式,在图中标注中间变量, 比如F1,F2和F3. , S = F2 F3= AF1 BF1 = A AB B AB = A AB + B AB = ( A + B )( A + B ) = AB + A B = A⊕ BC = F1 = AB = AB真值表C = F1 = AB = ABS= F2 F3 = AF1 BF1 = A AB B AB = A AB + B AB = ( A + B )( A + B ) = AB + A B = A⊕ B真值表该电路实现两个一位二进制数相加的功能.S 是它们的和,C是向高位的进位.由于这一加法器电路没有考虑低位的进位, 所以称该电路为半加器. 根据S和C的表达式,将原电路图改画成左图所示的逻辑图逻辑图.例2:分析下图的逻辑功能. :分析下图的逻辑功能.A B&AB&AABABF&ABBF = A B A B = A B + A B = A B + A BF = AB+ AB = AB + AB真值表A0 0 1 1B0 1 0 1F1 0 0 1同或门A B =1 FF = A⊕B特点:输入相同为" ; 特点:输入相同为"1"; 输入不同为" . 输入不同为"0".例3:分析下图的逻辑功能. :分析下图的逻辑功能.& A B&ABAB A&F&ABBF = AB A ABB= AB A + ABB( = A + B A + A + B B = AB+ AB ) ( )F = AB+ AB真值表异或门F0 1 1 0A0 0 1 1B0 1 0 1A B=1FF = A⊕B特点:输入相同为" ; 特点:输入相同为"0"; 输入不同为" . 输入不同为"1".例4:多变量输出组合逻辑设计举例: A,B,C三个车间,M,N两台发动机,M是N的2倍. 1个车间开工,启动N发动机; 2个车间开工,启动M发动机; 3个车间开工,启动M,N发动机.输入 A B C 0 0 0 0 0 1 0 1 0 0 1 1输出 M N 0 0 0 1 0 1 1 0输入 A B C 1 0 0 1 0 1 1 1 0 1 1 1输出 M N 0 1 1 0 1 0 1 1M = ABC + A BC + ABC + ABC = BC + AC + AB = AB BC ACA BC&&&M&例5 试用74LS138译码器实现逻辑函数:F ( A, B, C ) = ∑ m (1,3,5,6,7)解:因为则Yi = mi (i = 0,1,2,…7)= m1 + m3 + m5 + m 6 + m 7 = m1 m3 m 5 m 6 m 7 = Y1 Y3 Y5 Y6 Y7F ( A, B, C ) = ∑ m (1,3,5,6,7)因此,正确连接控制输入端使译码器处于工作状态,将 Y1 ,Y3 ,Y5 , 6 , 7 经一个与非门输 Y Y 出,A2,A1,A0分别作为输入变量A,B,C,就可实现组合逻辑函数.F ( A, B, C ) = ∑ m (1,3,5,6,7) = Y1 Y3 Y5 Y6 Y7例6试用八选一电路实现F = ABC + ABC + ABC + ABC解:将A,B,C分别从A2,A1,A0输入,作为 , , 输入变量,把Y端作为输出F.因为逻辑表达式中的各乘积项均为最小项,所以可以改写为F ( A, B, C ) = m 0 + m3 + m5+ m 7根据八选一数据选择器的功能,令D0 = D3 =D5 =D7 =1 D1 = D2 =D4 =D6 =0 S=0 = 具体电路见图3-21:真值表对照法注意变量高低位顺序!A 0 0 0 0 1 1 1 1B 0 0 1 1 0 0 1 1C 0 1 0 1 0 1 0 1 F 1 0 0 1 01 0 1例4 下图是由双4选1数据选择器74LS153和门电路组成的组合逻辑电路.试分析输出Z与输入X3, X2,X1,X0之间的逻辑关系.解: (1)划分功能块本题只有一块MSI电路,可以只划分一个功能块.(2)分析功能块的功能2 通过查74LS153的功能表,知道它是一块双4选 1数据选择器.其中:A1,A0是地址输入端,Y是输出端;74LS153的控制输入端为低电平有效;数据选择器处于禁止状态时,输出为0.图3-27电路的输出端是Z,Z=1Y+2Y;输入- , 端为X3,X2,X1,X0.当X3=1时,2S=1,1S= = , = 0,数据选择器2处于禁止状态,而数据选择器1处于工作状态;当X3=0时,数据选择器1处于禁止状态,数据选择器2处于工作状态.显然,图3-27电路构成了一个8选1数据选择- 器,其输出为Z,地址输入端为X3, X1 , X0. 图3-27电路可用图3-28的功能框图来表示. -图3-28 8选1功能框图(3)分析整体电路的逻辑功能把图3-27电路看成一个8选1数据选择器,可得出例3-7电路的功能表.表3-15 例3-7电路的功能表X3 X2 X1 X0 0 ××× 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 Z 1 1 1 0 0 0 0 0 0分析电路的功能表,当X3X2X1X0为 8421BCD码0000～～ 1001时,电路的输出为1,否则输出为0. 可见该电路可实现检测8421BCD 码的逻辑功能.例3-9 图3-30是3-8线译码器74LS138和8选1数据选择器74LS151组成的电路,试分析电路的逻辑功能.图3-30 例3-9电路解:(1) 划分功能块电路可划分为两个功能块: ① 3-8线译码器74LS138, ② 8选1数据选择器74LS151. (2)分析功能块的逻辑功能 3-8线译码器74LS138和8选1数据选择器74LS151的逻辑功能,这里不再重述.(3)分析整体电路的逻辑功能D0～D7和Y0～Y7 对应相连,b2b1b0=a2a1a0时, L=1;否则,L=0.该电路实现了两个3位二进制数的"相同"比较功能.例:利用线译码器分时将采样数据送入计算机. 利用线译码器分时将采样数据送入计算机.总线三态门EA三态门EB三态门EC三态门EDABY0Y1 Y 2CY3DA0 A12-4S工作原理:(以为例) 工作原理:(以A0A1=00为例) :( 为例总线脱离总线三态门EA三态门EB三态门EC三态门EDA 0BY0Y1 Y 22-4线译线译码器全为1 全为 CY3D 0 0A0 A1S构成两位串行进位全加器. 例:用一片SN74LS183构成两位串行进位全加器. 用一片构成两位串行进位全加器 D2 C D1串行进位snan bn cn-1A2 B2全加器cnsnan bn cn-1A1 B1全加器cn.(采用两片例1:七位二进制数比较器.(采用两片 ) :七位二进制数比较器.(采用两片85)高位片A>B ) (2) (A>B)L ( ) A=B 74LS85 A=B)L (AB低位片(A>B)L ) ( ) A=B 74LS85 A=B)L (AB A>C,则A最大;若最大; , ; , 最大 AB)L ) (A=B)L ) (AB)L ) (A=B)L ) (AB A>BA3B3 A2B2 A1B1 A0B0C3 C2 C1 C0A=B A=B A>B A>BA A1A3B3 A2B2 A1B1 A0B0A3 A2 A1 A0 B3 B2 B1 B04-2 S3 S2 S1 S0 Y 0000 A 0001 A+B 0010 A+/B 0011 1 0100 AB 0101 B 0110 A nxor B 0111 /(A+/B) 1000 A/B 1001 A xor B 1010 /B 1011 /(AB) 1100 0 1101 /A(B) 1110 /A/B 1111 /A 一个简单的逻辑运算器电路M=S3AB+S2AB N=S1B+S0B+A Y=M XOR N4位算术逻辑单元位算术逻辑单元74181 位算术逻辑单元4-6(1)F=ABC+ABC=B(AC+AC )=B(AC AC) =B(AC AC) F=ABC+ABC=ABAC+ACBC =AC(AB+BC ) = AC(AB BC ) = AC(AB BC )4-7(2)A被减数减数低位的借位被减数B减数被减数减数C低位的借位 D本位差向高位借位本位差E向高位借位本位差ABC DE 000 00 001 11 010 11 011 01 100 10 101 00 110 00 111 11D=∑m(1,2,4,7) E=∑m(1,2,3,7)4-7(2)D=∑m(1,2,4,7) E=∑m(1,2,3,7)4-7(2)D=∑m(1,2,4,7) E=∑m(1,2,3,7)4-12输入A 输入 1A0 输出Y 输出 3Y2Y1Y0Y3=A1A1A0 Y3Y2Y1Y0 00(0) 0101(5) 01(1) 0110(6) 10(2) 1001(9)11(3) 1110(14)Y2=A1A0 Y1=A0 Y0=A04-140 A1B1 A0B1 0 0 0 A1B0 A0B0A1A0 B1B0A1B0 A0B0 A1B1 A0B1 00Y3 D3 Y2 D2 Y1 D1 Y0 D04-17A被减数减数低位的借位被减数B减数被减数减数C低位的借位 D本位差向高位借位本位差E向高位借位本位差D=∑m(1,2,4,7) =Y1+Y2+Y4+Y7 =Y1+Y2+Y4+Y7 E=∑m(1,2,3,7) =Y1+Y2+Y4+Y70 A B CABC DE 000 00 001 11 010 11 011 01 100 10 101 00 110 00 111 11全减器参考电路1 参考电路1用异或门输入用开关输出用探针用集成芯片用门电路全减器用译码器参考电路2 参考电路2输出用探针.输入用逻辑字发生器全减器参考电路 3用数据选择器输入用逻辑字发生器输出用逻辑分析仪. A B C Sn Cn4-20 CD 00 01 11 10 AB 00 01 11 1 10 1 1 1 1 10 0 0 0 0 0 0 00 0 1 1 1 1 1 14-20 CD 00 01 11 10 AB 00 01 11 1 10 C 0 AB 00 0 01 11 10 1 0 1 0 1 1 1 1 1 1 10 0 0 0 0 1 1 10 04-20 C 0 AB 00 0 01 11 10 1 0 1 0 1 1 1 0 1CD 00 01 11 10 AB 00 01 11 1 10 1 1 1 1 10 0B 0 A 0 0 1 CB A1 C 0 04-21(1) CD 00 01 11 10 AB 1 1 00 1 01 11 10 1 1 D D C 0 AB 00 1 01 11 10 0 1 1 11 D 0 D D /D 0 D0 D D /D4-21(1)1 1 0 1 0 0 0 1CD 00 01 11 10 AB 1 1 00 1 01 11 10 1 1 1 10 1 1 0 0 0 0 14-21(2) CD 00 01 11 10 AB 1 1 00 1 01 11 1 10 1 1 1 1 11 1 0 1 0 0 0 01 0 1 0 1 1 1 14-21(2) CD 00 01 11 10 AB 1 1 00 1 01 11 1 10 1 C 0 AB 00 1 01 11 1 1 D 1 1 1 1 11 D 0 0 /D /D 1 10 010 /D /D1。