3 衍射强度
- 格式：ppt
- 大小：771.00 KB
- 文档页数：45
文档推荐
-
测量单缝衍射的光强分布页数:11
-
单缝衍射光强分布实验报告页数:6
-
单缝衍射光强分布的测定页数:4
-
单缝衍射光强分布的测定页数:3
-
实验单缝衍射光强分布研究页数:10
-
单缝衍射与光强分布(大物实验)页数:7
-
单缝衍射光强分布的测定页数:3
下载文档原格式
合集下载
第三章 衍射强度
Ab = Ae f1e iφ1 + Ae f 2 e iφ2 + ...... Ae f n e iφn = Ae ( f1e iφ1 + f 2 e iφ2 + ...... f n e iφn ) = Ae ∑ f j e
j =1 n iφ j
1、结构因子 、
我们可以用一个电子散射波振幅作为单位来度量一 个晶胞的散射波的振幅。
2 e 2 0Ie I来自 ree为电子电荷，m为电子质量，ε0为真空介电常数， c为光速
re 2 1 + (cos 2θ ) 2 ] Ie = I0 ( ) ×[ R 2
分析汤姆逊公式可以看出电子对X射线散射的特点 1、散射X射线的强度很弱。 假定R=1cm，2θ=0处 Ie/I0-=7.94×10-23 2、散射X射线的强度与电子到观测点之间的距离的平方成 反比。这是时很容易理解的。 3、不同方向上，即2θ不同时，散射强度不同。平行入射X 射线方向(2θ=0 或180°)散射线强度最大。垂直入射X射 线方向(2θ=90或270°)时，散射的强度最弱。为平行方向 的1/2。其余方向则散射线的强度在二者之间。 上式中的中的第二项决定了不同方向上散射强度是不同的。 所以也将其称为偏振因子或极化因子。 在以后的X射线衍射实验中大家可以观察到，在物相的X射 线的衍射图谱中，随着2θ的增大，物相的衍射峰的强度整 体降低。
⑴ 目测法比较确定 ⑵ 仪器测量 ⑶ 计算确定
衍射线强度测量示意图
I
Im I Im （220）γ I
I
（200）α
当精度要求不高时，可用最大强度Imax来表示相对强度。
如何确定X射线衍射强度? 分析的思路：晶体可以看成是一个个晶胞组成 的，晶胞又是由许多的原子组成的，原子又由 电子和一个原子核组成。我们的分析思路就是 从一个电子到一个原子，再到晶胞（多个原子） 来讨论晶胞的对X射线的衍射强度，最后讨论下 多晶体样品对X射线的的衍射强度。
高等结构分析第九章x射线多晶体衍射
常用衍射几何： Debye-Scherres几何，细条状样品 Bragg-Brenteno几何，平板状样品
从衍射图上可得到的信息： 衍射峰的位置、强度、峰形（峰宽）
二 衍射峰位置的测量和应用
1. 测量方法：
1）峰顶法、眼估法、微分法、拟合法 2）中点法 3）质心法
2. 点阵常数的测定和应用
sin 2 N k k 式中|pk|为小于Nk的任意整数，此时： 0 2 sin k 在两个极大值之间有Nk-1个极小
实际小晶体
累积能量EHKL：
E KF 2 LPTAV
e 4 1 3 2 1 cos 2 2 2 M T E I0 4 2 F ( )e AV 2 2 c m w Vu 2 sin 2
wi wi(1 ws )
若K=KiH/KsL已知，即可求出 wi
I iH K iH 0.5 K iH K I sL K sL 0.5 K sL
增量法是另一种值得一提的内标法。
（3）无标法：需同时有若干个成分相同、但组成量 不同的样品才能使用
3）定量相分析法应用举例
（1）结晶度的测定
（3）注意 1）d为主，I/I1为辅 2）要全对上 3）小d值，强I/I1的衍射线比较重要
4）考虑到实验灵敏度和分辨率的提高
5）多相混合物中，注意低含量相 峰少而弱
（4）应用
1）物态判断：晶态非晶态 药物多相态： 巴比妥类药物及甾体类药物有70% 磺胺类药物的40% 磺胺–5–甲氧嘧啶，一种为无定形、二种为水合物、 三种为晶态 头孢菌素各有8~10种溶剂合物 不同相态的药物，有的药性相近，有的完全不同 氯霉素，其A型是无效的，B型有效 两种不同晶型阿斯匹林,血清中水杨酸盐浓度II型大 于I型 磺胺–5–甲氧嘧啶在研磨时会转变为IV型
第三章 X射线衍射强度
温度因子
e
2 M
IT I
式中：IT — 原子热振动影响时的强度 I — 理相状态的强度 热振动的方向无规则性，使得非衍射方 向散射强度↑，增加衍射花样背底。
5 吸收因子 A(θ )
试样对x-ray的吸收造成衍射强度的衰减。
无吸收A(θ
)＝1，吸收越多，其值越小。 圆柱状试样的A(θ )是试样 l 和半径r的 函数，可通过查表求得。 1 板状试样的A(θ )与θ 无关， A( ) 2
角顶 Cs (0,0,0) FHKL = f Cs + f Cl e H + k + L = 偶数 F = f Cs+ f Cl 强度高 （110）（200）（211）… H + k + L= 奇数 F = f Cs – f Cl 强度低 （100）（111）（210）…
1 1 1 体心 Cl（ 2 , 2 , 2 ） iπ(H+K+L)
2 多重性因子 P
表示多晶体中同族晶面｛HKL｝的等同晶面
数。
P值越大，晶面获得衍射的几率越大，对应
的衍射线越强。
d同
θ同 衍射线重叠在同一衍射线环上。
P数值随晶系及晶面指数而变化。
例：
立方晶系（a
= b = c α=β=γ=90°）
P100= 6 四方晶系（a = b≠c α=β=γ=90°） P100= 4 P001= 2
系统消光
衍射线I=0，衍射线消失，称为系统消光。
（原子在晶胞中的位置不同引起某些方向 衍射线的消失--点阵消光）。
尽管满足衍射条件，因F
= 0使衍射线消失
的现象。
对于体心点阵，可以产生衍射的晶面为
第3章 X射线的衍射强度
1 1 1 2 i h k l F f 1 e 4 4 4
2) 当hkl全为奇数时，Ff=Fa。h+k+l=2n+1，其中n为任 意整数，则有
1 e
i
2
h k l
1 cos
2
h k l i sin
I＝A2
实际上，晶体要产生x射线衍射，x射线的波长应当 与晶体中原子间距在同一数量级。
与入射x射线平行的方向上(XX’): 相位差为0，所以Aa=ZAe 除了XX’方向：各电子的散射波之 间存在一定的相位差。 如在YY’方向上a、b两个电子产 生的散射波的波程差为CB-AD，
会产生干涉作用。 由于原子半径的尺度比x射线的波长的尺度要小，所以各电子的
四、一个晶胞对x射线的衍射
1、复杂点阵的衍射分析
简单点阵只由一种原子组成，每个晶胞只有一个原子，它 分布在晶胞的顶角上，单位晶胞的散射强度相当于一个原 子的散射强度。 复杂点阵晶胞中含有n个相同或不同种类的原子，它们除 占据单胞的顶角外，还可能出现在体心、面心或其他位置。 复杂点阵的衍射特点 （1）任何复杂点阵都是由完全相同且平行的几个简单点阵 镶嵌而成的； （2）整个复杂点阵的衍射可以看做是由各个简单点阵及基 点原子在相同方向的衍射合成结果； （3）复杂点阵的可能衍射方向不可能多余其中任何一个简 单点阵的衍射方向，只能减少或相等。
假定一个晶胞中有n个原子， 它们的坐标分别为u1v1w1、u2v2w2……unvnwn； 每个原子的原子散射因子分别为f1、f2、f3…… fn ；它们的散射波的振幅为 Aef1、Aef2、Aef3……Ae fn 各原子散射波与入射波的位相差分别为φ1、φ2、φ3、……φn。 那么，这n 个原子的散射波互相叠加合成的整个晶胞的散射波的振幅Ab为
2) 当hkl全为奇数时，Ff=Fa。h+k+l=2n+1，其中n为任 意整数，则有
1 e
i
2
h k l
1 cos
2
h k l i sin
I＝A2
实际上，晶体要产生x射线衍射，x射线的波长应当 与晶体中原子间距在同一数量级。
与入射x射线平行的方向上(XX’): 相位差为0，所以Aa=ZAe 除了XX’方向：各电子的散射波之 间存在一定的相位差。 如在YY’方向上a、b两个电子产 生的散射波的波程差为CB-AD，
会产生干涉作用。 由于原子半径的尺度比x射线的波长的尺度要小，所以各电子的
四、一个晶胞对x射线的衍射
1、复杂点阵的衍射分析
简单点阵只由一种原子组成，每个晶胞只有一个原子，它 分布在晶胞的顶角上，单位晶胞的散射强度相当于一个原 子的散射强度。 复杂点阵晶胞中含有n个相同或不同种类的原子，它们除 占据单胞的顶角外，还可能出现在体心、面心或其他位置。 复杂点阵的衍射特点 （1）任何复杂点阵都是由完全相同且平行的几个简单点阵 镶嵌而成的； （2）整个复杂点阵的衍射可以看做是由各个简单点阵及基 点原子在相同方向的衍射合成结果； （3）复杂点阵的可能衍射方向不可能多余其中任何一个简 单点阵的衍射方向，只能减少或相等。
假定一个晶胞中有n个原子， 它们的坐标分别为u1v1w1、u2v2w2……unvnwn； 每个原子的原子散射因子分别为f1、f2、f3…… fn ；它们的散射波的振幅为 Aef1、Aef2、Aef3……Ae fn 各原子散射波与入射波的位相差分别为φ1、φ2、φ3、……φn。 那么，这n 个原子的散射波互相叠加合成的整个晶胞的散射波的振幅Ab为
第三章 X射线衍射强度
由此可见，图3-2（a）中的（001） 晶面会参于衍射，而（b）中（001）面却 不产生衍射，也就是说原子位置改变，衍 射强度改变。
二 . 结构因素的概念
1. 系统消光——因原子在晶体中的位置不同或 原子种类不同，衍射线相互干涉，造成在某些 方向上衍射线强度减弱甚至消失的现象称之系 统消光。
2. 结构因数——定量地表征原子排布以及原子种 类对衍射强度影响规律的参数。即晶体结构对 衍射强度影响规律的参数。
晶体的衍射强度与参加衍射晶粒数目成正比.
∵ 参加衍射的晶粒分数＝(cosθΔθ)/2 ∴ 这一数目与衍射角有关，即I ∝ cosθ。
也将这一项称为第二几何因子。
⑶单位弧长的衍射强度（第三几何因子，即 衍射线位置对强度测量的影响）
意义：描述了衍射线所处位置不同对衍射强度的影 响，即2θ↓衍射线圆弧半径↓，单位弧长上的强度↑。
2.三种衍射几何对衍射强度的影响规律
⑴.晶粒大小的影响（第一几何因子）
由于实际晶体的不完整性、入射线也不可能是绝对 单色的，且不会绝对平行而是具有一定的发散角。因此， 衍射线的强度尽管在满足布拉格方程的方向上最大，但 偏离一定的布拉格角时也不会为零，故衍射曲线呈山峰 状，具有一定的宽度，而不是严格的直线。
2
当2θ=90。时
1 cos2 2
2对x射线的散射
1. 原子核对X-ray的散射
由于散射波强度与引起散射的粒子 质量成反比，原子核质量是电子质量的1840 倍，因此原子核引起的散射强度极弱，可忽 略不计。
2 . 原子中Z个电子对X-ray的散射
⑴ . 首先假设原子中的电子集于一点，即所有 电子散射波之间无位相差，则原子序数为Z的原 子对X-ray散射波振幅Aa为电子散射波振幅Ae的 Z倍，即 :
3. X射线衍射强度
exp[2i(hxj kyj lz j )] ＝cos2 (hxj kyj lzj) i sin 2 (hxj kyj lzj)
注意：
计算结构因数时要把晶胞中的所 有原子考虑在内。
结构因数表征了晶胞内原子的种 类，原子的个数，原子的位置对衍射 强度的影响。
结构因数的计算例
2
f {1 exp[i(h k)]}
当 h+k = 偶数时（h, k为全奇.全偶），F = 2f， I 4 f 2
当 h+k = 奇数时（h, k为奇.偶混合），F = 0，I = 0
底心晶胞h, k为全偶.全奇时衍射强度不为零。 h, k为奇偶混合时消光。
(3) 体心晶胞（体心立方, 体心正方, 体心四方)
I相对
P
F
2
1 cos2 2 sin2 cos
A( )e2M
P : 多重性因子； F：晶胞结构因数； A(θ): 吸收因子； e -2M : 温度因子 ；
角因子：1 cos2 2 sin2 cos
德拜－谢乐法的衍射线相对强度
I相对
P
F
2
1 cos2 2 sin2 cos
式中
I0: 入射X射线强度； λ : 入射X射线波长；
R : 与试样的观测距离；e：电荷的电量；m：电荷的质量
V : 晶体被照射的体积； Vc : 单位晶胞体积；
P : 多重性因子；
｜F｜2 晶胞结构因数；
A(θ): 吸收因子； e -2M : 温度因子 ；
＝
1 cos2 2 sin2 cos
与1′的波程差（DE+EF）为λ/2，故θ方向上产生相消干涉。
注意：
计算结构因数时要把晶胞中的所 有原子考虑在内。
结构因数表征了晶胞内原子的种 类，原子的个数，原子的位置对衍射 强度的影响。
结构因数的计算例
2
f {1 exp[i(h k)]}
当 h+k = 偶数时（h, k为全奇.全偶），F = 2f， I 4 f 2
当 h+k = 奇数时（h, k为奇.偶混合），F = 0，I = 0
底心晶胞h, k为全偶.全奇时衍射强度不为零。 h, k为奇偶混合时消光。
(3) 体心晶胞（体心立方, 体心正方, 体心四方)
I相对
P
F
2
1 cos2 2 sin2 cos
A( )e2M
P : 多重性因子； F：晶胞结构因数； A(θ): 吸收因子； e -2M : 温度因子 ；
角因子：1 cos2 2 sin2 cos
德拜－谢乐法的衍射线相对强度
I相对
P
F
2
1 cos2 2 sin2 cos
式中
I0: 入射X射线强度； λ : 入射X射线波长；
R : 与试样的观测距离；e：电荷的电量；m：电荷的质量
V : 晶体被照射的体积； Vc : 单位晶胞体积；
P : 多重性因子；
｜F｜2 晶胞结构因数；
A(θ): 吸收因子； e -2M : 温度因子 ；
＝
1 cos2 2 sin2 cos
与1′的波程差（DE+EF）为λ/2，故θ方向上产生相消干涉。
3 衍射强度解析
• 本章我们将讨论X射线衍射强度
• 从一个电子、一个原子、一个晶胞、一 个晶体、粉末多晶循序渐进地介绍它们 对X射线的散射问题.
• 最后讨论粉末多晶体的衍射强度问题.
一、关于衍射强度
** 单位时间内通过与衍射方向相垂直的单位面积 上的X射线光量子数目。 **绝对强度的测量既困难又无实际意义。 **衍射强度常用同一衍射图中各衍射线强度 (积分 强度或峰高)的相对比值即相对强度表示.
Ia＝f 2 Ie
**f－原子散射因子, f≤Z. **物理意义：某原子散射波的振幅相当于电子散 射波振幅的倍数。
2、一个晶胞对X射线的衍射
• 简单点阵只由一种原子组成，每个晶胞只有一个原子， 它分布在晶胞的顶角上，单位晶胞的散射强度相当于 一个原子的散射强度。 • 复杂点阵晶胞中含有n个相同或不同种类的原子，它 们除占据单胞的顶角外，还可能出现在体心、面心或 其他位置。 • 复杂点阵单胞的散射波振幅应为单胞中各原子的散射 振幅的合成。由于衍射线的相互干涉，某些方向的强 度将会加强，而某些方向的强度将会减弱甚至消失。 这种规律称为系统消光（或结构消光）。
2 = ( ZAe ) 2 = Z 2 Ie I a = Aa
** 即一个原子散射波的强度是一个电子散射波强 度的Z2倍。
(2) 实际情况
实际原子中的电子对 X 射线的散射情况（见图）将原 子中的电子看成是集中在一点上的这种处理是不准确 的。因为实际上电子是按照电子状态分布在原子空间 的不同位置上，故各电子的散射波之间是存在位相差 的，这一位相差使得合成波的强度减弱。衍射强度为：
度变为0）。
**对衍射强度作出系统而全面的研究 ,就要依靠结 构因子。当 X 射线照射到晶体中某个晶胞时，该晶 胞中各原子的散射波具有不同的位相和振幅，其合 成波的强度为：
第三章X射线衍射强度gqf详解
Modern Analytical Instruments and Technology for Materials 7
X射线衍射强度理论包括运动学理论和动力学理论，前者 只考虑入射X射线的一次散射，后者考虑入射X射线的多 次散射。
X射线衍射强度涉及因素较多，问题比较复杂。一般从基 元散射，即一个电子对X射线的（相干）散射强度开始， 逐步进行处理。
（原子散射因子）
晶胞内 各原子 散射波
合成
一个晶胞对X射 线的散射强度 （结构因子）
引入吸收因 子、温度因 子、多重性
因子
（粉末）多 晶体衍射
（积分）强 度
温度对强度 的影响
吸收对强度 的影响
等同晶面数 对强度的影
响
小晶体 内各晶 胞散射 波合成
单位弧长衍 射强度
参加衍射的晶 粒（小晶体）
数目
一个小晶体对X射线 的散射强度与衍射
（积分）强度 （干涉函数）
X射线衍射强度问题的处理过程
Modern Analytical Instruments and Technology for Materials 9
3.2 一个电子对X射线的散射 P15
电子在入射X射线电场矢量作用下会产生受迫振动。获得变 加速运动的电子，作为新的波源向四周辐射与入射X射线频 率相同并具有确定周相关系的电磁波。
Chapter 3
X射线衍射强度
The Diffracted Intensity of X-Ray
Modern Analytical Instruments and Technology for Materials
本章主要内容
了解影响衍射强度的各种因素，多重 因子，角因子，吸收因子，温度因子 和结构因子。
X射线衍射强度理论包括运动学理论和动力学理论，前者 只考虑入射X射线的一次散射，后者考虑入射X射线的多 次散射。
X射线衍射强度涉及因素较多，问题比较复杂。一般从基 元散射，即一个电子对X射线的（相干）散射强度开始， 逐步进行处理。
（原子散射因子）
晶胞内 各原子 散射波
合成
一个晶胞对X射 线的散射强度 （结构因子）
引入吸收因 子、温度因 子、多重性
因子
（粉末）多 晶体衍射
（积分）强 度
温度对强度 的影响
吸收对强度 的影响
等同晶面数 对强度的影
响
小晶体 内各晶 胞散射 波合成
单位弧长衍 射强度
参加衍射的晶 粒（小晶体）
数目
一个小晶体对X射线 的散射强度与衍射
（积分）强度 （干涉函数）
X射线衍射强度问题的处理过程
Modern Analytical Instruments and Technology for Materials 9
3.2 一个电子对X射线的散射 P15
电子在入射X射线电场矢量作用下会产生受迫振动。获得变 加速运动的电子，作为新的波源向四周辐射与入射X射线频 率相同并具有确定周相关系的电磁波。
Chapter 3
X射线衍射强度
The Diffracted Intensity of X-Ray
Modern Analytical Instruments and Technology for Materials
本章主要内容
了解影响衍射强度的各种因素，多重 因子，角因子，吸收因子，温度因子 和结构因子。
3.3 衍射强度
2 2
0
当一奇两偶时： F 0 f
2 2
0
§2.衍射强度
④底心点阵
原子数M=2，原子坐标(u,v,w)为
0,0,0; 1/2,1/2,0
| F |2 | f m exp[2 i (um H vm K wm L)] |2
m 2 1 | f1 exp[2 i(0 H 0 K 0 L)] f 2 exp[2 i( 1 H K 0 L )] | 2 2
m
| f1 exp[2 iLz ] f 2 exp[2 iL( z 1 4 )]
2 3 f3 exp[2 iL( z 1 )] f exp[2 iL ( z )] | 4 2 4 2 3 | f exp[2 iLz ] (1 exp[ 1 iL ] exp[ iL ] exp[ iL ] | 2 2
f 2 |1 exp[ i( H K )] exp[ i( H L)] exp[ i( K L)] |2
§2.衍射强度
讨论:
H、K、L全为偶数；e ni cos n i sin n (1) n F 4 f
2 2
16 f 2
H、K、L全为奇数；e ni cos n i sin n (1) n F 4 f
| F |2 | f m exp[2 i(um H vm K wm L)] |2
m 1 | f1 exp[2 i(0 H 0 K 0 L)] f 2 exp[2 i( 1 H 2 2 K 0 L)] 2 1 1 1 f3 exp[2 i( 1 H 0 K L )] f exp[2 i (0 H K L )] | 4 2 2 2 2
0
当一奇两偶时： F 0 f
2 2
0
§2.衍射强度
④底心点阵
原子数M=2，原子坐标(u,v,w)为
0,0,0; 1/2,1/2,0
| F |2 | f m exp[2 i (um H vm K wm L)] |2
m 2 1 | f1 exp[2 i(0 H 0 K 0 L)] f 2 exp[2 i( 1 H K 0 L )] | 2 2
m
| f1 exp[2 iLz ] f 2 exp[2 iL( z 1 4 )]
2 3 f3 exp[2 iL( z 1 )] f exp[2 iL ( z )] | 4 2 4 2 3 | f exp[2 iLz ] (1 exp[ 1 iL ] exp[ iL ] exp[ iL ] | 2 2
f 2 |1 exp[ i( H K )] exp[ i( H L)] exp[ i( K L)] |2
§2.衍射强度
讨论:
H、K、L全为偶数；e ni cos n i sin n (1) n F 4 f
2 2
16 f 2
H、K、L全为奇数；e ni cos n i sin n (1) n F 4 f
| F |2 | f m exp[2 i(um H vm K wm L)] |2
m 1 | f1 exp[2 i(0 H 0 K 0 L)] f 2 exp[2 i( 1 H 2 2 K 0 L)] 2 1 1 1 f3 exp[2 i( 1 H 0 K L )] f exp[2 i (0 H K L )] | 4 2 2 2 2
衍射强度理论
原子是由原子核和核外电子组成。原子核相对于 电子来说质量大得多，根据汤姆逊散射强度公式， 原子核对波的散射效应比电子小得多。在讨论原子 散射问题时，可以忽略原子核的散射作用，只考虑 核外电子对波的散射作用。因此，讨论原子的衍射 强度问题最终归结为电子对波的散射强度问题了。
根据这一思路，我们遵循从简单到复杂、由易 到难原则，分别从单个电子→原子→晶胞→理想 晶体→实际晶体→多晶（粉晶）等步骤对Ｘ射线 的散射强度问题展开讨论．
Ac Ae j 1 f j e
n
i j
结构振幅的概念
一个晶胞的散射振幅Ac ，实际是晶胞中全部电子相 干散射的合成波振幅。晶胞的散射振幅与一个电子的 散射波振幅的比值称为结构振幅，用F表示：
Fhkl
Ac Ae
j 1 f j e
n
i j
考虑到原子在晶胞中的坐标（xj，yj，zj），某晶面 （hkl）的结构振幅F hkl为：
G ( g hkl )
2
sin( N1h ) sin( h )
sin 2 ( N1h ) sin ( h )
2
sin 2 ( N 2 k ) sin ( k )
2
sin 2 ( N 3l ) sin 2 ( l )
N1 ,
2
sin( N 2 k ) sin( k )
N3 1 imnp p 0
e
G(g(hkl))称之为干涉函数．由指数函数的性质可将
干涉函数表示为如下形式：
G ( g hkl )
2
sin 2 ( N1h ) sin ( h )
2
sin 2 ( N 2 k ) sin ( k )
2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 有序化使无序固溶体因消光而失却的衍射线复出
现，这些被称为超点阵衍射线。 • 根据超点阵线条的出现及其强度可判断有序化的 出现与否并测定有序度。
§3-3 多晶体的衍射强度
• 本小节讨论最广泛应用的粉末法的衍射强度问题. • 在粉末法中影响衍射强度的因子有如下五项: • （1） 结构因子(上节已讨论)
• 本章我们将讨论X射线衍射强度
• 从一个电子、一个原子、一个晶胞、一 个晶体、粉末多晶循序渐进地介绍它们 对X射线的散射问题.
• 最后讨论粉末多晶体的衍射强度问题.
一、关于衍射强度
** 单位时间内通过与衍射方向相垂直的单位面积 上的X射线光量子数目。 **绝对强度的测量既困难又无实际意义。 **衍射强度常用同一衍射图中各衍射线强度 (积分 强度或峰高)的相对比值即相对强度表示.
度变为0）。
**对衍射强度作出系统而全面的研究 ,就要依靠结 构因子。当 X 射线照射到晶体中某个晶胞时，该晶 胞中各原子的散射波具有不同的位相和振幅，其合 成波的强度为：
2 FHKL
n n 2 = f k cos 2p ( mc H + PK K + q K L + f k sin 2p ( mk H + PK K + q k L k =1 k =1
• A(θ)-吸收因子
• r-试样直径
• 线吸收系数-μl
• 这样的吸收与θ有关。
• 平板试样的吸收因子，在入
射角与反射角相等时，吸收 与θ无关。
四、温度因子
＊＊前面所讲的各节，均将晶体中的原子看作是 处于理想平衡位置的结点上。 ＊＊实际上，晶体中原子是处在连续不断的热振 动状态下，必然给衍射带来影响． 1.晶胞膨胀； 2.衍射线强度减小；
• 395℃以下, AuCu3为有序态，此时Au原子占据晶 胞顶角位置，Cu原子则占据面心位置。Au原子坐 标(000)，Cu原子坐标，（0,1/2,1/2)（1/2,0,1/2)、 （1/2,1/2,0）.
• 代入公式，结果是：
• 1）当 H、K、L全奇或全偶时，F2=(fAu+3fCu )2
• 2）当H、K、L奇偶混杂时，F2=(fAu+fCu )2=0
(3)不同的掠射角，参与衍射的晶粒数目不同。
**这样X射线衍射强度将受到X射线入射角、参与衍射 的晶粒数、衍射角的大小等因素的影响。
• 将上述几种因素合并在一起，构成洛伦兹因子:
• （1/sin2θ）（cosθ）（1/sin2θ）= cosθ/ (sin2θ)2
= 1/4 sin2θcosθ
• 洛伦兹因子与极化因子合并，则有：
h－普朗克常数 ma－原子的质量 k－玻尔兹曼常数：1.38×10－8尔格· 度
Θ－特征温度，某些物质的特征温度可查附录8（P261）
Θ T－试样的绝对温度， = x
－德拜函数。附录7(P260)
T
五，粉末多晶的衍射强度 • 综合所有因数，Ｘ射线的衍射积分强度为：
• 德拜法的衍射相对强度
• 衍射仪法的衍射相对强度
2
F
2
HKL
－晶胞的散射能力，即结构因子
fk－原子散射振幅，即原子散射因子
K－单胞中的原子个数
mk、pk、qk－原子在晶胞中的坐标
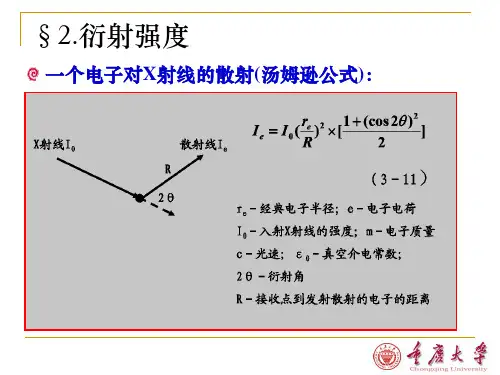
1、一个电子对X射线的散射
• 根据电磁波理论，当入射线与原子内受核束缚较紧
的电子相遇，光量子能量不足以使原子电离，但电
子可在X射线交变电场作用下发生受迫振动，这样电
子就成为一个电磁波的发射源，向周围辐射与入射X
第三章 X射线衍射强度
§3-1 引言
•X射线衍射理论能将晶体结构与衍射花样有机地 联系起来，它包括衍射线束的方向、强度和形状。
•衍射线束的方向由晶胞的形状大小决定,由Bragg 方程描述。 •衍射线束的强度由晶胞中原子的位置和种类决 定,Bragg方程无法描述衍射强度的大小。 •衍射线束的形状大小与晶体的形状大小相关。
• （2）多重性因子
• （3） 角因子（包括极化因子和罗仑兹因子）
• （4） 吸收因子
• （5） 温度因子
（2） 多重性因子
• 对多晶体试样，把晶面间距相同，晶面上原子排 列规律相同的晶面,称为等同晶面.由布拉格方程 知它们具有相同2θ，衍射线分布同一圆锥面上.
• 通常将同一晶面族中等同晶面组数P称为衍射强度 的多重性因子。在其他条件相同的情况下，多晶 体中某种晶面的等同晶面数越多，衍射线越强。 • 这一影响在强度公式中，以多重性因子Phkl的形 式出现。
R－由试样到照相底片上的衍射环间的距离
e. m－电子的电荷与质量, C－光速 V－试样被入射X射线所照射的体积. VC－单位晶胞的体积 cm3, F 2HKL －结构（振幅）因子 PHKL－多重性因子, φ（θ）－角因子, e-2M－温度因子 A（θ）－吸收因子
§3-2 结构因子
** 复杂点阵衍射 X射线时，通常会削弱某些方向的 衍射强度，也会使某些方向上的衍射消失（衍射强
3、面心点阵
单胞中有四种位置的原子，它们的坐标分别是（000） (0,1/2,1/2）（1/2,0,1/2)、（1/2,1/2,0）
1）当H、K、L全为奇数或全为偶数时, F2=16f 2 2）当H、K、L为奇偶数混杂时（2个奇数1个偶数或2个偶数1 个奇数）,F2=0 3)面心立方点阵只有指数为全奇或全偶的晶面才能产生衍射， 如（111）、（200）、（220）（311）、（222)等。能够出 现的衍射线，其指数平方和之比是：3：4：8：11；12： 16…=1；1.33：2.67：3.67：4：5.33…(书14页的消光规律)
衍射强度公式的适用条件
• (1)存在织构时，衍射强度公式不适用！
• (2)对于粉末试样或多晶体材料，如果晶粒尺寸粗
大，会引起强度的衰减，此时强度公式不适用．
六、衍射强度的测量
衍射强度的测量方法一般有三种 目测比较法，显微光度计法，计数器法
**立方晶系中的等同晶面数:
（100）晶面族的P为6 （111）晶面族的P为8 （110）晶面族的P为12 **{hho}是{hoo}晶面族获得衍射几率的二倍。
4、多重性因子Phkl 的计算
（1）立方晶系
1.可简单地变更h、k、l的顺序并改变各指数的正 负号（其晶面间距不变），所得可能的排列数目 即为多重性因子:Phkl＝48 2.有时两种晶面的h、k、l不同，但晶面间距却相 等。如{333}、{511}面,两种晶面的算术平均值: Phkl = 16
晶胞中所有原子相干散射的合成波振幅为:
单位晶胞中所有原子相干散射叠加的波即为结构因子, 即以一个电子散射波振幅为单位所表征的晶胞散射波 振幅,用F表示:
原子坐标为uvw的hkl晶面的结构因子为:
结构因子的计算
1、简单点阵 • 单胞中只有一个原子，基坐标为（000），原子散 射因数为f，根据上式计算为:
• 该种点阵结构因数与HKL无关，即HKL为任意整数 时均能产生衍射，例如（100）、（110）、（111）、 （200）、（210）…。
2、体心点阵
• 单胞中有两种位置的原子，即顶角原子（000）,体心原子 (1/2,1/2,1/2).
• 1）当H+K+L=奇数时，F2=0,即该晶面的散射强度为零，这 些晶面的衍射线不可能出现，如（100）、（111）、 （210）、（300)等。 2)当H+K+L=偶数时，F2=4f 2,即体心点阵只有指数之和为 偶数的晶面可产生衍射，例如（ 110 ）、（ 200 ）、（ 211) 等 。 这 些 晶 面 的 指 数 平 方 和 之 比 是 （ 12+12 ） ： 22 ： （22+12+12）：（32+12）…=2：4：6：8：10…
• 由于质子的质量是电子的1840倍，散射强度只有
电子的1／(1840)2，可忽略不计。
• 物质对X射线的散射可以认为只是电子的散射。
• 相干散射波虽然只占入射能量的极小部分，但由
于它的相干特性而成为X射线衍射分析的基础。
2、一个原子对X射线的散射
(1) 当一束 x 射线与一个原子相遇，原子核的散射 可以忽略不计。如果原子序数为Z的原子都集中在 一点，则各电子散射之间不存在位相差，一个原 子的散射X射线的强度为:
（ 2 ）非立方晶系：可根据相应的晶面间距公
式来考虑：例如四方晶系：（ 100 ）面的面间
距与（ 001）面间距不等 : {100}面的 Phkl＝4 , {001}面的Phkl＝2. *** 多重性因素往往可用表格查出：见附录 5 （P258）
二、角因子（极化因子和罗仑兹因子）
角因数φ（θ）是由一系列与掠射角有关的因素组成。
3.产生非相干散射。
＊如果某原子在某一瞬间偏离衍射晶面的距离为 E´，在布拉格方向上光程差为2E´sinθ．
＊ E´ 很小，光程差不可能等于波长λ的整数倍。 热振动散射波在该方向将减弱，因此，在计算强 度时乘上一个小于1的因数，即温度因子：
e
-2 M
=e
12h2 f ( x) 1 sin2 q + ) 2 ( ma Θk x 4 l
Ia＝f 2 Ie
**f－原子散射因子, f≤Z. **物理意义：某原子散射波的振幅相当于电子散 射波振幅的倍数。
2、一个晶胞对X射线的衍射
• 简单点阵只由一种原子组成，每个晶胞只有一个原子， 它分布在晶胞的顶角上，单位晶胞的散射强度相当于 一个原子的散射强度。 • 复杂点阵晶胞中含有n个相同或不同种类的原子，它 们除占据单胞的顶角外，还可能出现在体心、面心或 其他位置。 • 复杂点阵单胞的散射波振幅应为单胞中各原子的散射 振幅的合成。由于衍射线的相互干涉，某些方向的强 度将会加强，而某些方向的强度将会减弱甚至消失。 这种规律称为系统消光（或结构消光）。