2012-13高等数学上期末试卷A

2012-2013学年第一学期《高等数学》期末试卷一、填空题（每小题4分，共28分）1.当0→x 时，()11312-+ ax 与1cos -x 是等价无穷小，则=a .2.函数()x x x x f nnn 2211lim +-=∞→的间断点为.3.设()x x xx y 2arcsin 2arctan 1ln 2+-++=，则()='0y .4.曲线x ey arctan =的凹区间为.5.若()()C x F dx x f +=⎰ ，且b at x +=，则()=⎰dt t f .6.设()25=f ，()350=⎰dx x f ，则()='⎰dx x f x 50.7.设()dt e x F xx t ⎰-=2，则()='x F .二、计算题（每小题6分，共36分）1.求极限ne e e x nxx x x +++→ 20ln 1lim .2.设x xe y 2=，求()n y .3.设()x y y =由方程组⎩⎨⎧=-+-+=01cos 1y t e t e x y t 所确定，求022=x dx y d 的值.4.设()x f 在1=x 处可导且()21='f ，求极限()()xx f x f x +--→11lim 0.5.求 ⎰-22a x x dx ，其中a 是非零常数.6.计算⎰+312ln 1e x x dx.三、综合题（满分36分）1.（本题7分）证明函数()⎪⎩⎪⎨⎧≤>-+=0,00,11x x x x x f 在0=x 处连续，但不可导.2.（本题7分）试证：当0>x 时，()x x x x <+<-1ln 212.3.（本题7分）试在曲线段()802<<=x x y 上求一点M 的坐标，使得由曲线在M 点切线与直线8=x ，0=y 所围成的三角形面积最大.4.（本题7分）求定积分dx x ee ⎰ 1ln .5.（本题8分）求由不等式θcos 3≤r 和θcos 1+≤r 所确定的公共部分的面积.。

2012-13-1高等数学（A ）期末考试参考答案及评分标准一、填空题 (本大题分5小题，每小题4分，共20分)1、()2,3--2、()0f x '-3、04、()()x x f e e f x ----5、8π 二、选择题 (本大题共5小题，每小题4分，共20分)1、C2、A3、C4、D5、B三、解答下列各题(本大题共3小题，每小题6分，共18分) 1、解：原式=tan 2tan 00011sec 1lim lim lim sin cos sin x x xx x x x x e x e e x x x x x --→→→=--⋅=⋅-……………每步2分 2、解：令sin x t =，则cos dx tdt =， 原式2sin cos cos t tdt t=⎰………………………………………………………………………2分 21cos 211sin sin 2222t tdt dt t t c -⎡⎤===-+⎢⎥⎣⎦⎰⎰………………………………………4分 [].1arcsin 212c x x x +--=…………………………………………………………6分 3、解：1(),P x x =sin (),x Q x x =于是所求通解为： 11sin dx dx x x x y e e dx C x -⎛⎫ ⎪ ⎪⎝⎭⎰⎰=⋅+⎰ln ln sin x x x e e dx C x -⎛⎫ ⎪⎝⎭=⋅+⎰1(cos ).x C x =-+……每步2分 四、解答下列各题(本大题共3小题，每小题7分，总计21分)1、解：当000x t y ===，，，()1(0)2t x t e x ''=+=　………………………………3分cos sin 0,(0)0y y e y t e t y y '''-+==…………………………………………6分 故，00x dy dx ==……………………………………………………………………7分 2、证明：()()()a TT a T a aT f x dx f x dx f x dx ++=+⎰⎰⎰………………………………………2分 00()()()a Ta a T x t T f x dx f t T dt f t dt +=+=+=⎰⎰⎰对后者，令，=⎰f x dx a ()0…………5分 所以，f x dx f x dx f x dx a a T a T a ()()()+⎰⎰⎰=+0=⎰f x dx T()0。

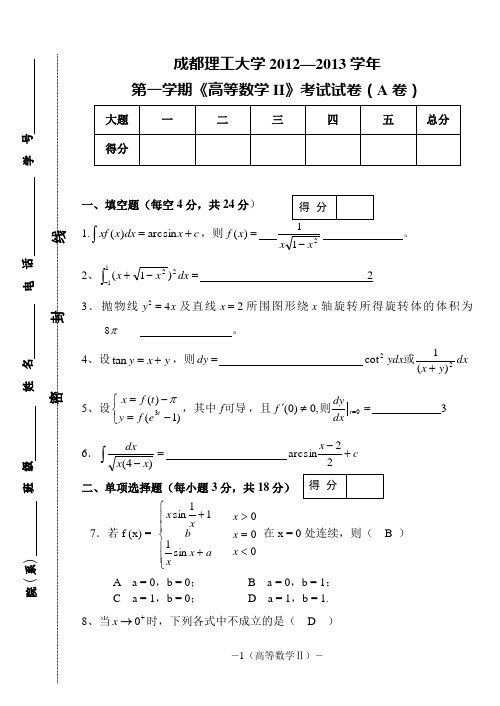
成都理工大学2012—2013学年 第一学期《高等数学II 》考试试卷（A 卷）一、填空题（每空4分，共24分） 1.⎰+=c x dx x xf arcsin )(，则)(x f2、=-+⎰-dx x x 2112)1(23．抛物线24y x =及直线2x =所围图形绕x 轴旋转所得旋转体的体积为8π 。

4、设y x y +=tan ，则=dy dx y x ydx 22)(1cot +或5、设⎩⎨⎧-=-=)1()(3te f y t f x π，其中可导f ，且=≠'=0,0)0(t dx dyf 则 36．=-⎰)4(x x dxc x +-22a r c s i n二、单项选择题（每小题3分，共18分） 7．若f (x) = ⎪⎪⎩⎪⎪⎨⎧++a x x b x x sin 111sin 000<=>x x x 在x = 0处连续，则（ B ） A a = 0，b = 0； B a = 0，b = 1； C a = 1，b = 0； D a = 1，b = 1. 8、当+→0x 时，下列各式中不成立的是（ D ）得 分得 分︵（A ）2sin x ～2x ； （B ）x tan ～x （C ）12-x e ～2x ； （D ）)1ln(x -～x ； 9、曲线xxe y 1=（D ）（A ）没有渐近线 （B ）仅有垂直渐近线（C ）仅有斜渐近线 （D ）既有垂直渐近线，又有斜渐近线10． 若1)0(='f ，则xx f x f x )()2(lim 0-→＝（ B ）(A)0； (B)1； (C)2； (D)不存在 11、设21)1()(lim,0)1()(21=-''='→x x f f x f x 具有二阶连续导数，且，则（ B ） A ．的极大值是)()1(x f f B ．的极小值是)()1(x f f C ．的拐点是曲线（)())1(,1x f y f = D ．以上答案均不对12、若()y f x =在(),-∞+∞上有二阶导数，()()f x f x -=-，且在(),0-∞内有()()0,0f x f x '''><，则在()0,+∞内有（ A ）A ()()0,0f x f x '''>> ；B ()()0,0f x f x '''<< ；C ()()0,0f x f x '''<>；D ()()0,0f x f x '''><三、计算题（每小题6分，共24分）13、. 求极限x x x )(sin lim 0+→ 解：x x x e x sin ln )(sin =， （2分）0)s i n c o s(l i m 1s i n ln lim sin ln lim 2000=-==+++→→→xx x xx x x x x x （3分） ∴原式10==e （1分）得 分14．.求极限3220cos )(limxtdtx t x x ⎰-→解：原式＝3220cos cos limx tdtx tdt t x xx ⎰⎰-→ （2分）＝220203cos cos 2cos limxxx tdt x x x x x --⎰→ （2分）＝xtdtxx 3cos 2lim00⎰-→＝3cos 2lim0xx -→＝32- （2分）15、若曲线d cx bx ax y +++=23在点0=x 处有极值0=y ，点)1,1(为拐点，求d c b a ,,,的值。

华南农业大学期末考试试卷（A 卷）2012~2013学年第1 学期 考试科目：高等数学A Ⅰ 考试类型：（闭卷）考试 考试时间： 120 分钟 学号 姓名 年级专业一、填空题（本大题共5小题，每小题3分，共15分）1．函数1y x=的定义域是 。

2．10lim(14)xx x →+= 。

3．设ln(sin )y x =，则dy = 。

4．不定积分1ln x xdx ⎰= 。

5．反常积分211dx x +∞-∞+⎰= 。

二、单项选择题（本大题共5小题，每小题3分，共15分）1．设1sin ,0(),0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在点0x =处必定 （ ） A ．连续但不可导 B ．连续且可导C ．不连续但可导D ．不连续，故不可导2．曲线1y x =在点1(,2)2处的切线方程是 （）A ．440y x -+=B ．440x y +-=C ．440y x --=D ．440x y --=3．设()f x 为连续函数，则()d f x dx =⎰ （ ） A ．()f x B ．()f x dx C ．()f x C + D ．'()f x dx 4．设0()(1)(2)xx t t dt Φ=--⎰，则'(0)Φ= （ ）A ．2-B ．1-C ．1D ．25．若函数()(),()f x f x x -=-∞<<+∞，在(,0)-∞ 内()'0f x >，且()''0f x <，则在(0,)+∞内有 （ ） A ．'()0,''()0f x f x >< B ．'()0,''()0f x f x >> C ．'()0,''()0f x f x << D ．'()0,''()0f x f x <>三、计算题（本大题共7小题，每小题7分，共49分）1. 求极限 0sin lim x xx e e x-→-。

南京工业大学2012-2013高等数学期末试卷A 及答案一、填空题（每小题3分，共36分）1.=⎪⎪⎭⎫⎝⎛+∞→∞→x y x xy 11lim ==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+∞→∞→∞→∞→⋅∞→∞→01lim111lim 11lim e xy xy yxyy x yxy y x y x 1 .2.函数),(y x z z =由方程0sin =+x y e xz 确定，则=-=-=∂∂xz z y xe x y x F F y z cos 1xz ex x y 2cos - . 3.设函数222lnz y x u ++=，则它在点)1,1,1(0-M 处的方向导数的最大值为33. 4.设函数y xy ax x y x f 22),(22+++=在点)1,1(-处取得极值，则常数=a 5-.5.空间曲线x z x y -==1,222在点)22,1,21(处的切线方程为 212211121--=-=-z y x .6.改变积分次序：==⎰⎰-dy y x f dx I x x 22020),(dx y x f dy y y ⎰⎰-+--2211111),( .7.设平面曲线L 为下半圆周21x y --=，则=⋅=⋅=+⎰⎰π2221211)(LLds ds y x π . 8.设∑为曲面22y x z +=在10≤≤z 的部分，则⎰⎰∑=xdS 0 .9.设,0,10,)(⎩⎨⎧<≤<≤-=-ππx x e x f x 则其以π2为周期的傅里叶级数在π=x 处收敛于)1(21πe + . 10.设321,,y y y 是微分方程)()()(x f y x q y x p y =+'+''的三个不同的解，且≠--3221y y y y 常数，则微分方程的通解为 1322211)()(y y y C y y C +-+- .11.函数x x f -=21)(展开为x 的幂级数的形式为)2,2(2101-∈∑∞=+x x nn n .12.微分方程x xe y xy =-'1的通解为 x xe Cx + . 二、计算下列各题（每小题6分，共18分）1.设),(xye xy f z =，)(x y ϕ=，其中ϕ,f 均为一阶可微函数，求dxdz . 解：)(221y x y e f xy x y f dx dz xy'+⋅'+-'⋅'= ))()(()()(221x x x e f xx x x f xyϕϕϕϕ'+⋅'+-'⋅'= 2.求曲面)(21422y x z +-=与平面2=z 所围立体的体积.解：所围立体在xoy 面的投影域4:22≤+y x D ，所围立体的体积 dxdy y x dxdy dxdy y x V D DD ⎰⎰⎰⎰⎰⎰+-=⎭⎬⎫⎩⎨⎧-+-=)(2122)](214[2222 πππθππ4482122202202=-=-⨯=⎰⎰rdr r d3.在曲面6632222=++z y x 上第一卦限部分求一点，使该点的切平面与已知平面1=++z y x 平行.解：设曲面在第一卦限的切点的坐标为),,(z y x M ，令=),,(z y x F 6632222-++z y x ，则切平面的法向量)6,4,2(),,(z y x F F F n M z y x ==, 已知平面1=++z y x 的法向量)1,1,1(1=n依题意1//n n，即令t z y x ===161412 代入曲面方程中解的2,3,6===z y x ，即切点坐标为)2,3,6(M . 三、计算下列各题（每小题6分，共18分） 1.设Ω是由锥面22y x z +=与半球面221y x z --=围成的空间区域，∑是Ω的整个边界的外侧，求曲面积分⎰⎰∑++zdxdy ydzdx xdydz .解：已知x z y x P =),,(，y z y x Q =),,(，z z y x R =),,(，由高斯公式有dv zR y Q x P zdxdy ydzdx xdydz ⎰⎰⎰⎰⎰Ω∑∂∂+∂∂+∂∂=++)(dr r d d dv ϕϕθππsin 33122040⎰⎰⎰⎰⎰⎰==Ωππ)22(31)221(23-=⨯-⨯⨯= 2.写出级数++++43227252321的通项，判别该级数的敛散性.若级数收敛时，试求其和. 解：该数项级数的通项为nn n u 212-=；级数为正项级数，由于 21121221lim lim1=-+⋅=∞→+∞→n n u u n nn n ，由比值审敛法知该级数收敛.令)1,1()()(22)12()(211111-∈-=-=-=∑∑∑∞=∞=-∞=x x s x xs x xn x x n x s n n n n nn ，则xxx dt ntdt t s n xn n n x-===∑⎰∑⎰∞=∞=-1)(1111， 于是2011)1(1)()(x dtt s dx d x s x -=⎥⎦⎤⎢⎣⎡=⎰， 又xxx x s n n -==∑∞=1)(12， 所以)1,1()1(1)1(2)(222-∈-+=---=x x x x x x x x x s ，于是3)1(21)12()21(21221=⎥⎦⎤⎢⎣⎡-+=-==∞=∑x n n x x x n s .3.求微分方程x e y y y 223=+'-''的通解.解：微分方程对应的齐次线性微分方程的特征方程0232=+-r r 的特征根为2,121==r r ，x e x f 2)(=的1=λ为特征方程的单根，则原方程的特解为x Axe y =*，代入原方程中得2-=A ,齐次线性微分方程的通解为x x e C e C Y 221+=,所以原方程的通解为=+=*y Y y x x x xe e C e C 2221-+.四、计算下列各题（每小题6分，共18分） 1.求函数22)(4),(y x y x y x f ---=的极值.解：由于x y x f x 24),(-=，y y x f y 24),(--=，令,0),(0),(⎩⎨⎧==y x f y x f yx 得驻点,22⎩⎨⎧-==y x 又 2),(-==y x f A xx ，0),(==y x f B xy ，2),(-==y x f C yy ，及4)()2,2(2-=--AC B ， 则点)2,2(-位极大值点，极大值为8)2(2)]2(2[4)2,2(22=-----=-f .2.求幂级数∑∞=-12)1(n nnn x 的收敛半径及收敛域. 解：令 1-=x t ，则 nn nn n n t n n x ∑∑∞=∞==-11212)1(，由于 212)1(2lim lim 11=+=+∞→+∞→n n n nn n n n a a ， 则收敛半径2=R .又当2-=t 时，级数∑∞=-1)1(n nn 收敛，当2=t 时，级数∑∞=11n n 发散，所以)2,2[-∈t ，即级数的收敛域为)3,1[-.3.设),()sin(y x x xy z ϕ+=，其中),(v u ϕ具有二阶偏导数，求yx z∂∂∂2.解：),(1),()cos(21yxx y y x x xy y x z ϕϕ'+'+=∂∂，)(),(1),(1)(),()sin()cos(222222122yxy x x y y x x y y x y x x xy xy xy y x z -⋅''+'--⋅''+-=∂∂∂ϕϕϕ五、（本题5分）求函数2),(22+-=y x y x f 在椭圆域}14|),{(22≤+=y x y x D 上的最大值和最小值.解：由于x y x f x 2),(=，y y x f y 2),(-=，令,0),(0),(⎩⎨⎧==y x f y x f y x 在D 内求得驻点)0,0(.在D 的边界上，设)14(2),,(2222-+++-=y x y x y x F λλ，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+==+-==+=)3(014),,()2(0212),,()1(022),,(22y x y x F y y y x F x x y x F y x λλλλλλ当0≠x ，由（1）得1-=λ，代入（2）得0=y ，在代入（3）得⎩⎨⎧=±=01y x ；同理当0≠y 得⎩⎨⎧±==20y x ；由于2)0,0(=f ， 3)0,1(=±f ， 2)2,0(-=±f ，所以最大值为3，最小值为2-.六、（本题5分）设在上半平面}0|),{(>=y y x D 内，函数),(y x f 具有连续偏导数，且对任意的0>t 都有),(),(2y x f t ty tx f -=，证明对D 内的任意分段光滑的有向简单闭曲线L ，都有0),(),(=-⎰dy y x xf dx y x yf L.解：由格林公式，对D 内的任意分段光滑的有向简单闭曲线L ，⎰⎰⎰----±=-1)],(),(),(),([),(),(D y xLdxdyy x yfy x f y x xf y x f dyy x xf dx y x yf .dxdy y x yf y x xf y x f y D x )],(),(),(2[1---±=⎰⎰ （*）由于函数),(y x f 具有连续偏导数，且对任意的0>t 都有),(),(2y x f t ty tx f -=，即),(),(2ty tx f y x f t =上式两端对t 求导有),(),(),(221ty tx f y ty tx f x y x tf '+'= 特取1=t 得),(),(),(2y x yf y x xf y x f y x += 由（*）式既有0),(),(=-⎰dy y x xf dx y x yf L。

某某省某某市2012-2013学年高一上学期期末考试数学试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．考生作答时，将答案答在答题卡上，在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回．参考公式：球的体积公式343V R π=，球的表面积公式24S R π=. 第I 卷一．选择题:本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列图形中,表示集合N M ⊆关系的韦恩图是（ ）2．已知直线10x my +-=与直线220x y -+=平行，则m 的值为（ ） A. 2- B.12-C. 2D.123.函数3()f x x =的图像关于（ ）A ．y 轴对称B ．坐标原点对称C ．直线x y =对称D ．直线x y -=对称4.直线l 的方程是5x =，圆C 的方程是22(2)9x y -+=,则直线l 与圆C 的位置关系是（ ）A. 相离B. 相切C. 相交D. 相交或相切5．已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ，则)]41([f f 的值是( )A. 91B. 41C. 4 D. 96．如图为函数ln y m x =+的图像，其中m 、n 常数，则下列结论正确的是 （ ） A ．0,1m n <> B ．0,1m n >> C ．0,01m n ><< D ．0,01m n <<<7．在用二分法求方程3210x x --=的一个近似解时，现已经确定一根在区间(1,2)内，则下一步可断定该根所在的区间为( )A ．(1.4,2)B ．(1,1.4)C ．3(1,)2D ．3(,2)28．已知函数22log (2)y x kx k =-+的值域为R,则k 的取值X 围是（ ）A .01k <<B 01k ≤< C.0k ≤或1k ≥ D.0k =或1k ≥ 9．在下列正方体中，有AB CD ⊥的是（ ）O 1 x yA B C D10. 若过点(4,0)A 的直线l 与曲线22(2)1x y -+=1)2(22=+-y x 有公共点，则直线l 的斜率的取值X 围为（ ）A ．[B ．(C ． [33-D ．(33- 11．点(4,2)P -与圆224x y +=上任一点连线的中点轨迹方程是( )A ．22(2)(1)1x y -++= B ．22(2)(1)4x y -++= C ．22(4)(2)4x y ++-=D ．22(2)(1)1x y ++-=12．已知函数()y f x =的定义域为D ，若对于任意的1x ，2x D∈()12x x ≠，都有()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭，则称()y f x =为D 上的凹函数．由此可得下列函数中的凹函数为（ ）A ．2log y x =B ．y =C ．3y x =D ．2y x =第 Ⅱ 卷（非选择题，共90分）二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13．设2.03=a ，π21log =b ，3..021⎪⎭⎫⎝⎛=c ，则c b a ,,从大到小的顺序为.14.过点()1,2P 引一直线，使其倾斜角为直线:l 30x y --=的倾斜角的两倍，则该直线的方程是_________________.15．给出下列四个命题：①若直线垂直于平面内的两条直线，则这条直线垂直于这个平面；②若直线与平面内的任意一条直线都垂直，则这条直线垂直于这个平面； ③若直线l α平面，直线m α平面，则l m ； ④若直线a 直线b ，且直线l a ⊥，则l b ⊥．其中正确命题的序号是．16．从点P 出发三条射线,,PA PB PC 两两成60°角，且分别与球O 相切于,,A B C 三点，若球的体积为43π，则OP 的距离为． 三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)定义在R 上的函数()y f x =是偶函数，当x ≥0时，2483f x x x =-+-（）. （Ⅰ）当0x <时，求()f x 的解析式；（Ⅱ）求()y f x =的最大值，并写出()f x 在R 上的单调区间（不必证明）．. 18．(本小题满分12分)如图， 在底面是菱形的四棱锥P ABCD -，60ABC ∠=︒，PA AC a ==，2PB PD a ==，点E 是PD 的中点．证明： （Ⅰ）PA ⊥平面ABCD ；（Ⅱ）PB ∥平面EAC ．19. (本小题满分12分)如图所示是一个几何体的直观图及它的三视图(其中主视图为直角梯形，俯视图为正方形，左视图为直角三角形，尺寸如图所示)，(Ⅰ)求四棱锥P ABCD -的体积；(Ⅱ)若G 为BC 的中点，求证：AE PG ⊥.20.(本小题满分12分)已知2()3g x x =--，()f x 是二次函数，当[1,2]x ∈-时，()f x 的最小值为1，且()()f x g x +为奇函数，求函数()f x 的表达式．44242222主视图左视图俯视图21．(本小题满分12分)已知圆M 过两点A (1，－1)，B (－1,1)，且圆心M 在20x y +-=上．(1)求圆M 的方程；(2)设P 是直线3480x y ++=上的动点，PC 、PD 是圆M 的两条切线，C 、D 为切点，求四边形PCMD 面积的最小值． 22．（本题满分12分）定义：对于任意x ∈[0,1]，函数()0f x ≥恒成立，且当12120,0,1x x x x ≥≥+≤时，总有1212()()()f x x f x f x +≥+成立，则称()f x 为G 函数．已知函数2()g x x =与()21xh x a =⋅-是定义在[0,1]上的函数．（1）试问函数()g x 是否为G 函数？并说明理由；（2）若函数()h x 是G 函数，某某数a 的值； （3）在（2）的条件下，利用函数图象讨论方程(2)(21)xg h x m +-+=(R)m ∈解的个数情况．高一期末测试卷数学参考答案与评分标准一．选择题1. C ；2．A ；3.B ；4.B ；5．A ；6．D ；7．D ；8．C ；9．A ；10.C ；11．A ；12．D ． 二.填空题13．a c b >>；14．1x =；15．②，④；16．3． 三.解答题17．解：（Ⅰ）设x ＜0，则0x ->，22()4()8()3483f x x x x x -=--+--=---， ············· 2分∵()f x 是偶函数，∴()()f x f x -=，∴0x <时，2()483f x x x =---． ················· 5分（Ⅱ）由（Ⅰ）知224(1)1(0)()4(1)1(0)x x f x x x ⎧--+≥⎪=⎨-++<⎪⎩， ············ 6分 ∴()y f x =开口向下，所以()y f x =有最大值(1)(1)1f f =-=． ···· 8分函数()y f x =的单调递增区间是（-∞，-1]和[0，1]；单调递减区间是 [-1，0]和[1，+∞)． ·············· 10分18．证明：（1）底面ABCD 为菱形，60ABC ∠=，AB BC CD DA AC a ∴=====． ··················· 2分PA AC =，PA AB a ∴==，PB =，PA AB ∴⊥，同理可证PA AD ⊥，···················· 4分又AB AD A =，PA ∴⊥平面ABCD ．················ 6分 （2）连结AC BD ，相交于O ，则O 为BD 的中点．E 为PD 的中点，PB OE ∴∥． ···················· 8分 又OE ⊂平面EAC ，PB ⊄平面EAC ， ··············· 10分 PB ∴∥平面EAC ． ························· 12分19.解(Ⅰ)由几何体的三视图可知，底面ABCD 是边长为4的正方形， ······· 2分PA ⊥面ABCD ，PA ∥EB ，且PA ＝42，BE ＝22，AB ＝AD ＝CD ＝CB ＝4， .... 4分∴V P －ABCD ＝13PA x S ABCD ＝13×42×4×4＝6423. .......................... 5分(Ⅱ)连BP ，∵EB AB ＝BAPA＝12，∠EBA ＝∠BAP ＝90°， .................. 7分 ∴△EBA ∽△BAP ，∴∠PBA ＝∠BEA ， ............................... 8分 ∴∠PBA ＋∠BAE ＝∠BEA ＋∠BAE ＝90°，∴PB ⊥AE . ................. 10分 又∵BC ⊥面APEB ，∴BC ⊥AE ，∴AE ⊥面PBG ，∴AE ⊥PG . ............ 12分 20. 解：设()(),02≠++=a c bx ax x f则()()()312-++-=+c bx x a x g x f ． 2分又()()x g x f +为奇函数，∴3,1==c a ．4分∴(),32++=bx xx f 对称轴2bx -= ．当22≥-b时，()f x 在[]2,1-上为减函数 ∴()f x 的最小值为()13242=++=b f ∴3-=b 又4-≤b ， ∴此时无解． 6分当221<-<-b 时，()14322min =-=⎪⎭⎫⎝⎛-=b b f x f ∴22±=b ∵2224-=∴<<-b b ，此时(),3222+-=x x x f 8分当12-≤-b时，()f x 在[]2,1-上为增函数∴()f x 的最小值为()141=-=-b f ∴3=b ，又满足2≥b ∴(),332++=x x x f 10分综上所述，(),3222+-=x x x f 或()332++=x x x f 12分21．解：(1)法一:线段AB 的中点为(0,0),其垂直平分线方程为0x y -=． ···· 2分解方程组0,20.x y x y -=⎧⎨+-=⎩所以圆M 的圆心坐标为(1,1)．故所求圆M 的方程为：22(1)(1)4x y -+-=． ············· 4分 法二:设圆M 的方程为：222()()x a y b r -+-=，根据题意得222222(1)(1),(1)(1),20.a b r a b r a b ⎧-+--=⎪--+-=⎨⎪+-=⎩·················· 2分解得1,2a b r ===．故所求圆M 的方程为：22(1)(1)4x y -+-=． ············· 4分 (2)由题知，四边形PCMD 的面积为1122PMC PMD S S S CM PC DM PD ∆∆=+=+. ············ 6分 又2CM DM ==,PC PD =，所以2S PC =，而PC ==即S = ························· 8分 因此要求S 的最小值，只需求PM 的最小值即可，即在直线3480x y ++=上找一点P ，使得PM 的值最小， 所以min3PM==， ·················10分所以四边形PCMD 面积的最小值为S ===················· 12分22．解：（1） 当[]0,1x ∈时，总有2g x x 0()=≥，满足条件①，1分当12120,0,1x x x x ≥≥+≤时，22222121212121212g x x x x x x 2x x x x g x g x ()()()()+=+=++≥+=+，满足条件② ································ 3分 （2）∵()21xh x a =⋅-是G 函数，∴210xa ⋅-≥，∴12x a ≥恒成立． ······ 4分 ∴a 1≥． ······························· 5分 由1212g x x g x g x ()()()+≥+ ，得1212x x x x a 21a 21a 21+⋅-≥⋅-+⋅-，即12xx a 121211[()()]---≤， ······················· 6分因为 12120,0,1x x x x ≥≥+≤所以 1x0211≤-≤2x0211≤-≤1x 与2x 不同时等于 1 11xx021211()()∴≤--<，11x x 0121211()()∴<---≤，11x x 1a 12121()()∴≤--- ·························· 7分 当12x x 0==时，11x x 1112121min ()()()=---，a 1∴≤， ··········· 8分综合上述a 的值为1. ··························· 8分 （3）根据⑵知： a=1，方程为x 2x 1421m -++-=， ············· 9分令x4tt 14[,]=∈ 方程为2t m 1t+=+ 图（略） ································ 10分 由图形可知：当7m 122{}(,]∈⋃时，有一解；当m 12(,]∈ 时，有二不同解；当7m 12(,)(,)∈-∞⋃+∞时，方程无解． ················ 2分。

2012-2013学年第一学期期末考试试卷高三数学（文科）第Ⅰ卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的 ）1．已知集合2{|1},{|20}A x x B x x x =≤=-<，则A B = （ ）A ．（0，1）B ．（1，2）C ．(]0,1D ．[)1,1-2．已知向量a =(1,2)-，b =(,2)x ，若a ⊥b ，则||b =( ) A ．5 B ．25 C ．5 D ．203．已知四棱锥P —ABCD 的三视图如右图所示，则四棱锥P —ABCD 的体积为（ ）A ．13B ．23C ．34D ．384．已知函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象如图所示，则()f x 的解析式是（ ）A ．()sin(3)()3f x x x R π=+∈B ．()sin(2)()6f x x x R π=+∈C ．()sin()()3f x x x R π=+∈D ．()sin(2)()3f x x x R π=+∈5．双曲线12222=-by a x 的离心率为3,则它的渐近线方程是A ．x y 2±=B ．x y 22±= C ．x y 2±= D ．x y 21±=6．在ABC ∆中，1310tan ,cos 210A B ==，则tan C 的值是（ ）A ．-1B ．1C ．3D ．-27．设m ，n 是两条不同的直线，,,αβγ是三个不同的平面，有下列四个命题： ①若,,;m m βαβα⊂⊥⊥则 ②若//,,//;m m αβαβ⊂则③若,,,;n n m m αβαβ⊥⊥⊥⊥则 ④若,,,.m m αγβγαβ⊥⊥⊥⊥则 其中正确命题的序号是 （ ）A ．①③B ．①②C ．③④D ．②③8．两个正数a 、b 的等差中项是5,2一个等比中项是6,,a b >且则双曲线22221x y a b -=的离心率e 等于 （ ）A ．32B ．53C ．133D ．139．由直线2+=x y 上的点向圆()()22421x y -++= 引切线，则切线长的最小值为( )A ．30B ．31C ．24D ．33 10．数列{}n a 中，372,1a a ==，且数列1{}1n a +是等差数列，则11a 等于（ ）A ．25-B ．12C ．23D ．511．三棱锥P-ABC 的三条侧棱PA 、PB 、PC 两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC 外接球的表面积是( )A ．202π B.252π C.50π D.200π12．已知函数(1)f x +是定义在R 上的奇函数，若对于任意给定的不等实数1x 、2x ，不等式1212()[()()]0x x f x f x --<恒成立，则不等式(1)0f x -<的解集为（ ）A ．()1,+∞B ．(),0-∞C ．()0,+∞D ．(),1-∞ 第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题，每小题5分，共20分。

高等数学（上）期末试卷2012-2013—昆明理工大学一、单项选择题（每小题4分，共24分）1.(1,0,1),= a (0,1,1),= b ()⨯⋅= a b a （ ）（A ）-1 （B ）0 （C ）1 （D ）22.设111()23+=+xx e f x e，则0=x 是()f x 的 （A ）可去间断点 （B ）跳跃间断点 （C ）无穷间断点 （D ）振荡间断点3. 已知(3)2'=f ，则0(3)(3)lim 2→--=h f h f h（ ） （A ）-1 （B ）1 （C ）-2 （D ）24. 设曲线方程为22sin(1)1-=-x y x ，则（ ） （A ）1=-y 是曲线的渐近线 （B ）0=y 是曲线的渐近线（C ）1=-x 及1=x 是曲线的渐近线 （D ）曲线没有渐近线5. 设函数()=y f x 由方程2=+xy x y 确定，则0==x dy （ ）（A ）ln 2dx （B ）(ln 21)-dx （C ）(ln 21)+dx （D ）ln 21-6. 下列级数中条件收敛的是（A ）1(1)1∞=-+∑n n n （B）1∞=n n （C ）211(1)∞=-∑n n n （D）1(1)∞=-∑n n 二、填空题（每小题4分，共24分）7、曲线sin 2cos ⎧=⎪⎨=⎪⎩t t x e t y e t在点(0,1)处的法线方程为 . 8、曲线2222232⎧=+-⎪⎨=--⎪⎩z x y z x y在xoy 面上的投影曲线的方程是 . 9、函数203()1=-+⎰xt x dt t t ϕ在区间[0,1]上的最小值为 . 10、设()2ln(1),0,0⎧+<=⎨+≥⎩ x x f x x a x 在0=x 处连续，则=a .11、不定积分2ln =⎰x xdx .12、定积分320sin =⎰xdx π .三.计算题（共8题，每题5分）13、求点0(2,3,4)-M 到直线312:231+-+==x y z L 的距离。

河北科技大学2012——2013学年《高等数学》（上册）期末考试A 卷一. 单项选择题（每小题4分，共20分）1. 设λ是常数，函数⎪⎩⎪⎨⎧≤>--=1,01,11cos )1(1)(x x x x x g λ处处可微，则必有( )A.1-<λB. 01<≤-λC. 10<≤λD. λ≤12. 设函数⎪⎩⎪⎨⎧≥+<+=0,10,1sin cos )(2x x x xx x x f 则0=x 是函数()f x 的( ) A. 可去间断点 B. 跳跃间断点 C. 振荡间断点 D.连续点3. 已知函数()f x 二阶导数连续，且0)0(=f ，2)(lim 20-=-→x f x x ，则0)0(=f （ ） A.是函数)(x f 的极小值 B.是函数)(x f 的极大值C.不是函数)(x f 的极值D.不一定是函数)(x f 的极值4. 设在区间],[b a 上0)(>x f ，0)(<'x f ，0)(<''x f ，令))((1a b a f S -=， ))](2([2a b b a f S -+=，))](()([213a b b f a f S -+=，则 ( ) A. 321S S S << B. 312S S S << C. 123S S S << D. 213S S S <<5. 已知θae r =，则从0=θ到πθ=的弧长为( )A.)1(-πe aB. )1(2-πe aC. πae 2D. )1(2πe a -二.填空题（每小题4分，共20分）1. 设函数()f x 二阶导数连续，且0)(lim 0=+→x x f x ，2)0(=''f ，则=++→x x x x f 10])(1[l i m . 2. 函数x e x y +=sin 上点)1,0(处的法线方程是 .3. 设1arcsin )1()(+-+=x x x x x x f ，则=')1(f .4. 设曲线2x y =与直线2=x 及x 轴所围成的图形的面积为A ，则=A .5.⎰-=+-+225)cos |11|(ln ππdx x xx . 三. 计算下列各题：（每小题7分，共35分）1. 求极限⎰⎰+→022020)]1[ln(sin lim 2x x x dt t t dt t .2. 已知参数方程为⎩⎨⎧-=+=tt y t x arctan )1ln(2（其中t 为参数），求y ''.3. 设⎪⎩⎪⎨⎧<+≥+=--0,)1(0,)1()(11x e x x x f x ，求定积分⎰-20)1(dx x f 的值. 4. 求不定积分⎰-dx x x 2)(sin .5.求曲线311-+=x y 的凹凸区间及拐点.四．解答下列各题（第一小题9分，第二小题8分，共17分）1. 设函数)(x f 在),(+∞-∞内有定义，且1)0(='f ，对任意的数y x ,恒有等式 xy y f x f y x f 2)()()(++=+成立，求函数)(x f 的表达式.2. 求曲线2x y =在区间)1,0(内的一条切线，使该切线与直线0=x ，1=x 和曲线2x y =所围成图形的面积最小.五. 证明题（8分）设函数)(x f ，)(x g 二阶可导，且当0>x 时，)()(x g x f ''>''，又)0()0(g f =，)0()0(g f '='，证明：当0>x 时，恒有)()(x g x f >.。