湖北省100所重点中学2012届高三10月联合考试(数学文)

湖北省100所重点中学2012届l0月高三联合考试地理试卷考生注意：1．本试卷分第I卷(选择题）和第II卷（非选择题）两部分，共100分。

考试时间90分钟.2．请将各题答案填在试卷后面的答题卡上。

3．本试卷主要考试内容：人教版必修l第一单元约占30％,第二单元约占40％，第三单元约占30％。

第I卷(选择题共44分)一、单项选择题(本题共22小题。

每小题2分，共44分。

在下列各个小题的四个选项中。

只有一个选项是最符合题目要求的)据悉，中国的火星轨道器“萤火一号”现已研制成功,2011年11月上旬，“萤火一号”将与俄罗斯研制的火星轨道器“火卫一土壤"一同发射至火星。

完成1—2题。

1．进入火星轨道的“萤火一号”属于①太阳系②地月系③总星系④银河系⑤河外星系A．①②③B．②③④C．③④⑤D．①③④2．美国的“凤凰号"火星探测器曾经利用仪器设备在火星的北极发现了水呈冰冻状态，其原因最有可能是A．火星北极引力大B．火星北极温度低C．火星大气气压高D．火星大气水汽含量大2011年8月23日晚上8时，开始于12日的第26届世界大学生夏季运动会胜利闭幕.完成3—4题.3．深圳大运会期间，地球大致运行到位置A．① B．② C．③ D．④4．深圳大运会举办期间,下列各城市白昼时间最长的是A．沈阳B．天津C．武汉D．三亚下图中,弧ab为地球大圆的一部分，a、b两点关于地心对称,c为孤ab的中点。

读图，完成5-6题。

5．下列关于a、b两点的叙述，正确的是A．a、b两点的纬度一定相同B．a、b两点的经度相同C．a、b两点的地方时相同D．a、b两点的线速度相等6．下列叙述中,与题意吻合的是A．c点一定位于赤道B．a、b之间的最短航程必须经过极点C．a、b两地的正午太阳高度可能相等D．a、b两地可能同时位于深夜2011年6月5日，智利南部普耶韦火山(位于安第斯山脉上）爆发,从火山口喷出的烟柱已高达l0公里。

松山学校校本课程 导学案 课 题7. 大变革的时代主备人刘家秀班级7时间学习 目标了解战国时期铁农具和牛耕的广泛使用和都江堰水利工程等情况；掌握商鞅变法的主要内容和历史作用。

重点 难点商鞅变法的主要内容和历史作用。

我国封建社会的形成。

学 习 过 程学法指导：※号标志的为重点知识须认真掌握 一、自主学习：(自读课文P36—P39页，完成下列问题。

20分钟 ) 1.______时期，我国开始出现铁农具。

_____时，铁农具使用反围扩大。

2.______末年已使用牛耕，_____时期牛耕进一步推广。

3.______和_____的推广，使土地利用率和农作物产量显著提高。

4._______时期，___国蜀郡太守______在岷江中游修筑______,是闻名世界的防洪灌溉工程 5.战国时期新兴地主阶级为了确立 ，发展 ，先后在各国掀起变法。

6.公元前_____年，商鞅在 支持下开始变法。

（变法的内容结合教材38页，加以识记。

） 7.经过商鞅变法，_____国的经济得到发展，军队战斗力不断加强，发展成为战国时期最富强的封建国家。

我国封建国家形成了。

8.封建社会的主要矛盾是 和 的矛盾。

二、合作探究（生生互助，师生互动，点拨释疑，共同提高）8—10′ 1.说一说，铁农具为什么能较快推广？ 2. 思考回答教材第39页的动脑筋 3.阅读材料： 卫鞅曰：“治世不一道，便国不法古。

故汤武不循古而王，夏殷不易礼而亡。

反古者不可非，而循礼者不足多。

”孝公曰：“善。

”以卫鞅为左庶长，卒定变法之令。

《史记·商君列传》 请回答： ⑴材料中“卫鞅”、“孝公”分别是指谁？ ⑵结合所学知识分析材料中的观点代表哪个阶级的利益？ ⑶卫鞅在哪国实现了这一理论？ 学生回头看（根据情况有重点的看书或背诵）3′—4′ 审阅人： 时间： 初中学习网，资料共分享！我们负责传递知识！。

湖北省100所重点中学2012届10月髙三联合考试物理试卷解析考生注意：1. 本试卷分第I卷（选择题)和第II卷(非选择题）两部分，共1OO 分.考试时间90分钟.，2。

请将各题答案填在试卷后面的答题卷上。

3. 本试卷主要考试内容：必修1占50％,必修2占50％.第I卷（选择题共40分）选择题部分共10小题。

在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确;全部选对的得4分，选对但不全的得2分，有选错或不答的得0分.1. 下列说法正确的是A。

质点、位移都是理想化模型B。

牛顿的三个定律都可以通过实验来验证C. 单位m、kg、s是一组属于国际单位制的基本单位D。

牛顿最早指出力不是维持物体运动的原因1.C解析：质点是理想化模型，位移是描述位置变化的物理量，选项A错误；牛顿的三个定律都是根据大量事实总结出来的，牛顿第一定律不能通过实验来验证，选项B错误；单位m、kg、s是一组属于国际单位制的基本单位，选项C正确;伽利略最早指出力不是维持物体运动的原因,选项D错误。

2. 如图所示，某质点沿半径为r的半圆弧由a点运动到b点，则它通过的位移和路程分别是A 2r方向向东πrB. r,方向向东πrC. 2r 方向向东2rD. 002.A解析：质点沿半径为r的半圆弧由a点运动到b点，它通过的位移大小是2r，方向为向东,路程为半圆弧长度，是πr。

选项A正确。

3. （2012湖北百校联考）下列有关超重和失重的说法，正确的是A. 无论物体处于超重还是失重状态，物体所受的重力总是不变的B。

做竖直上抛运动的物体处于完全失重状态C。

在沿竖直方向向上运动的升降机中出现失重现象时，升降机一定处于上升过程D. 在沿竖直方向向上运动的升降机中出现失重现象时，升降机一定处于下降过程3。

AB解析：无论物体处于超重还是失重状态，物体所受的重力总是不变的，选项A正确；做竖直上抛运动的物体，其加速度为重力加速度，物体处于完全失重状态,选项B正确;在沿竖直方向向上运动的升降机中出现失重现象时，升降机一定处于向上加速或向下减速运动过程,选项CD错误；4.（2012湖北百校联考）我国“嫦娥一号"探月卫星发射后，先在“24小时轨道”上绕地球运行（即绕地球一圈需要24小时)。

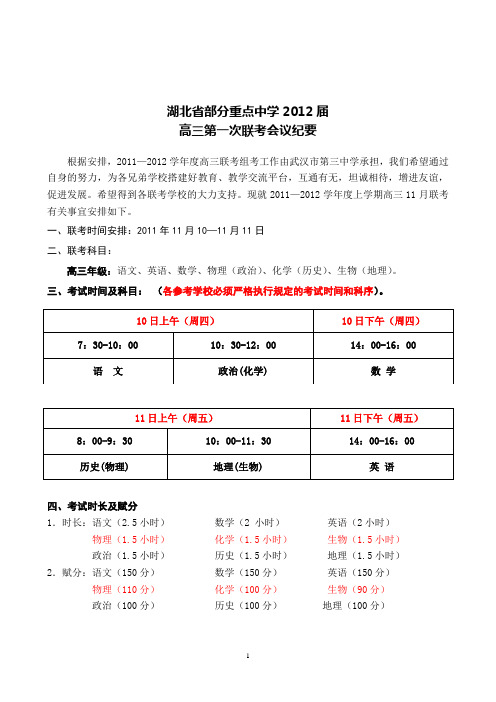
湖北省部分重点中学2012届高三第一次联考会议纪要根据安排，2011—2012学年度高三联考组考工作由武汉市第三中学承担，我们希望通过自身的努力，为各兄弟学校搭建好教育、教学交流平台，互通有无，坦诚相待，增进友谊，促进发展。

希望得到各联考学校的大力支持。

现就2011—2012学年度上学期高三11月联考有关事宜安排如下。

一、联考时间安排：2011年11月10—11月11日二、联考科目：高三年级：语文、英语、数学、物理（政治）、化学（历史）、生物（地理）。

三、考试时间及科目：（各参考学校必须严格执行规定的考试时间和科序）。

四、考试时长及赋分1．时长：语文（2.5小时）数学（2 小时）英语（2小时）物理（1.5小时）化学（1.5小时）生物（1.5小时）政治（1.5小时）历史（1.5小时）地理（1.5小时）2．赋分：语文（150分）数学（150分）英语（150分）物理（110分）化学（100分）生物（90分）政治（100分）历史（100分）地理（100分）五、考试和命题范围：2011——2012学年度高三11月联考命题建议范围七、命题要求：1．方向性：研读课标、教材、课改地区考纲及全国新课改高考试卷，领会课改精神，把握课改命题方向性。

2．阶段性：体现高三第一轮复习的阶段性特征，试卷应注重基础，覆盖面广，突出主干，追求命题的针对性、科学性、规范性、严谨性。

3．层次性：试卷要有较好的区分度，试题难度：易、中、难比例为5:3:2。

我们拟定以540—560分为理科重点线，能较好地区分各校重本层次学生。

4、创新性：推陈出新，力求创新，杜绝陈题。

5．保密性：命题、审题、组考等环节务必做好保密，各参考学校必须严格执行规定的考试时间和科序顺序，不得提前考试或变更科序。

6、各校各学科备课组长命题的建议和要求，希望命卷老师认真学习和领会。

命题质量是联考成功的保障，请各命题学校务必选聘好命题教师，建议选派有经验有实力的老师命题。

考试时间：2012年11月14日上午8:00～10:00 本卷三大题22小题 试卷满分150分 一、选择题：每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 与直线垂直且在轴上截距为的直线方程为 （ ） A．B． C． D． 2. 从300名学生（其中男生180人，女生120人）中按性别用分层抽样的方法抽取50人参加比赛，则应该抽取男生人数为 （ ） A．27 B．30 C．33 D．36 3. 先后随机投掷枚正方体骰子，其中表示第枚骰子出现的点数，表示第枚骰子 出现的点数，则点在直线上的概率为 （ ） A． B． C． D． 4. 从装有4只红球，4只白球的袋中任意取出2只球，记事件=“摸出2只白球”，事件=“摸出1只白球和一只红球”，则下列说法正确的是 （ ） A．事件是必然事件 B．事件A是不可能事件 C．事件与事件是对立事件 D．事件与事件是互斥事件 5. 直线被圆所截得的弦长为，则a的值为 （ ） A．或 B．1或3 C．或6 D．0或4 6. 阅读右面的程序框图，则输出的S为 （ ） A． B． C． D． 7. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记 录的产量x（吨）与相应的生产能耗y（吨）的几组数据：x3456y2.5t44.5依据上表可知回归直线方程为，则表中t的值为 ( ) A． 3 B．3.15 C．3.5 D．4.5 8. 正方形的边长为2，在其内部取点P，则事件“、、、的面积均大于”的概率是 ( ) A． B． C． D． 9. 关于x的方程有两个不同的实数根，则实数的取值范围是 （ ） A． B． C． D． 10若，现用随机模拟的方法估计与及x轴围成的面积S，用计算机先产生两组（每组30个）在区间上的均匀随机数和，由此得到30个点 ，现数出其中满足 的点有10个，则由随机模拟的方法可估计得到面积S为 （ ） A．6 B． C． D．5 二、填空题：每小题5分，共35分.请将答案填在答题卡对应题号的位置上. 答错位置，书写不清，模棱两可均不得分. 11. 任意投掷两枚骰子,则出现点数相同的概率是 . 12. 在区间上随机取一个数a，则函数有零点的概率为 . 13. 直线l过圆的圆心且与平行，则直线l的方程为 . 14. 将参加数学竞赛的100名学生编号为：001,002，… ，100，采用系统抽样的方法抽取一个容量为10的样本，已知随机抽取的一个号码为003，则从编号为019到056的号码中，抽取的人数为 人. 15. P为直线上的动点，过P作圆的切线，则切线长的最小值是 . 16. 将n表示为 （）,当时， ；当时，为0或1.记为上述表示中为1的个数，例如：， ， 故， ， 则：. 17. 一组数据中共有7个整数：m，2，2，2，10，5，4，且，若这组数据的平均数、中位数、众数依次成等差数列，则m的值为 . 5小题，共65分，解答应写出文字说明，证明过程或演算步骤. 18．（本小题满分12分） 根据下面的程序写出其运行的结果，并画出相应的程序框图． 19．（本小题满分12分） 一个袋中有5个大小相同的球，其中3个红球2个白球，从中任取2个球. （Ⅰ）求至少取到1个白球的概率; （Ⅱ）求取到的球颜色相同的概率． 20.（本小题满分13分） 记事件“直线与圆相交”. （Ⅰ）若将一颗骰子投掷两次得到的点数分别为a、b，求事件A发生的概率； （Ⅱ）若实数a、b满足，求事件A发生的概率． 21.（本小题满分14分） 某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题： （Ⅰ）求频率分布直方图中间的矩形的高为多少? （Ⅱ）若要从分数在之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在之间的概率; （Ⅲ）依据上频率分布直方图，求该班数学成绩的平均分数估计是多少. 22.（本小题满分14分） 圆C过点，圆心在y轴的正半轴上，且与圆外切. （Ⅰ）求圆C的方程; （Ⅱ）直线l过点交圆C于A、B两点，若以AB为直径的圆经过坐标原点O， 求直线l的方程. 二、填空题 12分 20. 解：（I）依题意：直线与圆相交， 则，得到：，又可知、均大于0， 故， 当时， 当时， 当时，， 事件发生的方法数为9，总的方法数为， 故事件发生的概率为 6分 （II）依题意为几何概型， 与公共的面积为： 直线与圆相交的弓形面积， ，故扇形的中心角为， 则弓形的面积， 故事件发生的概率为. 13分 , 矩形的高为. 5分 （II）的人数为：25×0.016=4人，又的人数为2人， 的人数有6人，从中取出2人的方法数是15种， 2份都在的方法数是6种， 故至少有一份分数在之间的概率为： 10分 （III） 该班数学成绩的平均分数估计为73.8分. 14分 解得：, 直线的方程为：.14分 S=0 i=1 WHILE i<=59 S=S+i i=i+2 WEND PRINT S END 第6题图。

湖北省100所重点中学2012届10月高三联合考试生物试卷考生注意：1．本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共100分。

考试时间90分钟。

2．请将各题答案填在试卷后面的答题卷上。

3．本试卷主要考试内容：(新课标人教版)必修l(60％)；必修2第1～3章(40％)。

第I卷 (选择题共50分)一、选择题(本大题共25小题，每小题2分，共50分。

在每小题给出的四个选项中，只有一项符合题意。

)1．下列能说明原核细胞和真核细胞具有统一性的是A．原核细胞具有与真核细胞相同的染色质B．原核细胞具有与真核细胞相同的细胞分裂方式C．原核细胞具有与真核细胞相同的细胞质D．原核细胞具有与真核细胞相同的细胞膜基本支架2．亲核蛋白是指在细胞核内发挥作用的一类蛋白质。

以下有关亲核蛋白的叙述不正确的是A．亲核蛋白在细胞质中合成B．亲核蛋白进入细胞核的方式与葡萄糖进入红细胞的方式相同C．亲核蛋白可能参与染色体的组成D．与DNA复制有关的酶可能属于亲核蛋白3．下列根据各概念图作出的判断，正确的是A．甲图可以表示植物细胞内储能物质b和糖原a的关系B．若乙中a和b分别代表DNA和RNA，则乙图可以代表原核细胞内的核酸C．丙图可体现出细胞生物膜系统c、核糖体a和线粒体b的关系D．丁图能体现酶c、蛋白质a和核糖核酸b的关系4．关于元素和化合物的叙述，正确的是A．蛋白质的多样性取决于肽键的多样性B．细胞膜上Na+的载体和质粒的基本单位一致C． P是DNA和ATP共有的元素D．ADP审含有两个高能磷酸键5．端粒是存在于真核生物染色体的末端，由DNA序列及其相关的蛋白质所组成的复合体；端粒酶是一种逆转录酶，由蛋白质和RNA构成。

由此可知，属于核糖体、端粒和端粒酶共同点的是A．都只存在于真核细胞中 B．都具有C、H、O、N、P等化学元素C．都与遗传信息的传递无关 D．都含有遗传物质6．下列有关生物膜的叙述，正确的是A．参与细胞膜组成的脂质只有磷脂B．用蛋白酶处理生物膜可改变其组成，不改变其通透性C．抗体的合成和分泌过程都与生物膜有关D．小鼠细胞与人体细胞的细胞膜在一定条件下能够发生融合7．右图是细胞核的结构模式图，下列关于各结构及功能的叙述正确的是A．①是所有生物遗传物质的载体B．所有细胞中核糖体的形成都与②有关C．③属于生物膜系统，把核内物质与细胞质分开D．④是大分子物质如DNA出入细胞核的通道8．用洋葱鳞片叶表皮制备“观察细胞质壁分离实验”的I临时装片，观察细胞的变化。

湖北省部分重点中学2011-2012学年度高三年级起点考试数 学 试 卷本卷满分：150分 试卷用时：120分钟第Ⅰ卷（选择题 共50分）一、选择题（本大题共10小题，每小题5分，共50分，每小题只有一项是符合题目要求的） 1.设全集U=R ，集合15{|||}22M x x =-≤，{|14}P x x =-≤≤，则()U C M P ⋂等于（ ） A ．}24|{-≤≤-x x B ．}31|{≤≤-x xC ．}43|{≤≤x xD ．}43|{≤<x x2.“1a =”是“直线0x y +=和直线0x ay -=相互垂直”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3.(理)定积分ln 20e xdx ⎰的值为（ ）(A)－1(B)1 (C)2e 1-(D)2e(文)抛物线28y x =-的焦点坐标是（ ） (A) (2,0)(B) (2,0)-(C) (4,0)(D) (4,0)-4．右图是某四棱锥的三视图，则该几何体的表面积等于 (A)34+(B)6+(C) 6+ (D)17+5．执行下面的程序框图，输出的S 值为（ ）A ．109 B ．187 C ．98 D ．526． 设函数()sin(2)3f x x π=+，则下列结论正确的是( )①．()f x 的图象关于直线3x π=对称②．()f x 的图象关于点(,0)4π对称③．()f x 的图象向左平移12π个单位，得到一个偶函数的图象④．()f x 的最小正周期为π，且在[0,]6π上为增函数A. ①③B. ②④C. ①③④D. ③7．已知函数 ()xf x a x b =+-的零点(,1)()x n n n Z ∈+∈ ，其中常数,a b 满足23,32a b==，则n 的值是（ ）。

A ．-2 B ．-1 C ．0 D ．18．在区间[,]22ππ-上随机抽取一个数x, cos x 的值介于0和12之间的概率为（ ）A ．12B ．23C ．13D ．6π9.直线3y kx =+与圆22(3)(2)4x y -+-=相交于M ，N两点，M N ≥,则k 的取值范围是（ ）3.[,0]4A -3.(,][0,)4B -∞-⋃+∞.[,33C - 2.[,0]3D - 10.已知在ABC ∆中，A C B 90∠=, BC 3AC 4==，.P 是A B 上的点，则点P 到AC BC ，的距离的积的最大值是( )A ． 2B ．3C ．2D ．第Ⅱ卷（非选择题 共100分）二、填空题（本大题共5小题，每小题5分，共25分，把答案填在题中横线上）11．某学校为了解高一男生的百米成绩，随机抽取了50人进行调查，右图是这50名学生百米成绩的频率分布直方图。

虎尾兰 长春藤 芦荟 龙舌兰 菊花 绿萝 扶郎花（又名非洲菊） 秋海棠 鸭跖草 学 而 不 思 则罔 回头看看你有何收获 一、细胞吸水的原理: 水分由浓度低 浓度高 二、根尖的结构包括：根冠、分生区、 伸长区、成熟区。

成熟区有大量根毛 , 是根吸收水分和无机盐的主要部位。

三、根吸水和失水的原理：根毛细胞 内溶液浓度比土壤浓度大,根吸水;根毛 细胞内溶液浓度比土壤浓度小,根失水。

四、水分和无机盐通过导管运输。

* 请同学们用镊子从培养皿中夹取一根萝卜条放入盐水中，再夹一根放入清水中，留下一根做对比。

* 这土块中包着茄子幼苗的什么器官？ * 绳子缠绕着大树的什么部位？显然，根对于植物体很重要，那根有什么作用呢 ？ * 看看这么多玉米的根，牢牢地伸到土壤中，大风也不易把它吹走，可见根有什么作用 ？ * 这根没伸到土壤中，而伸到培养液中，这又有什么作用呢？ * 红薯可以吃，和鱼、肉、奶、但、蛋一样，是因为其中有 什么？说明这根有什么功能？农民还可以在春天把红薯种到地里，会长出很多红薯幼苗，这又说明红薯具有什么功能？ * 阅读课本P99第二节 根的这些功能中最主要的是哪个？这说明： （板书）第二节 绿色植物的生长需要水和无机盐 所以植物通过根吸收水分和无机盐 （板书）二 植物对水分和无机盐的吸收 那么根是如何吸收水分的呢？土壤中溶液的浓度对根吸水的过程有什么影响吗？（板书）1.观察溶液浓度的大小对植物吸水的影响 那溶液的浓度与什么有关呢？ * 让我们分清溶液中有什么？ * 很显然，清水的浓度小，而盐水的浓度大。

溶液浓度的大小对植物吸水会有什么影响呢 让我们先来看个动画 * 我们先来看一个动画。

然后也亲自做一下。

* 注意这个实验中烧杯的大小，里面液体的多少，萝卜条的长短粗细是否大致相同，唯一不同的是两个烧杯中一个是清水，另一个 是盐水现在让我们取出清水、盐水中的萝卜条，放入培养皿中，和培养皿中的萝卜条对比一下，你会看出那些不同？注意观察长度和硬度的变化以及粗细的变化。

湖北省百所重点中学2015届高三十月联合考试试题文科试题【试卷综评】本次试卷从题型设置、考察知识的范围等方面保持稳定，试题难度适中，试题在考查高中数学基本概念、基本技能和基本方法等数学基础知识，突出三基，强化三基的同时，突出了对学生能力的考查，注重了对学科的内在联系和知识的综合、重点知识的考查，以它的知识性、思辨性、灵活性，基础性充分体现了考素质，考基础，考方法，考潜能的检测功能。

试题中无偏题，怪题，起到了引导高中数学向全面培养学生数学素质的方向发展的作用。

突出考查数学主干知识 ,侧重于中学数学学科的基础知识和基本技能的考查；侧重于知识交汇点的考查。

全面考查了考试说明中要求的内容。

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知集合22{|60}{|50}M x Z x x N x x=∈-+>=-<，则M N等于A．{}1,2,3B．{}1,2C．{}2,3D．{}3,4【知识点】交集及其运算. A1【答案解析】B 解析：由M中不等式变形得：x（x﹣6）＜0，解得：0＜x＜6，即M={1，2，3，4，5}；由N中不等式解得：﹣＜x＜，即N=（﹣，），则M∩N={1，2}．故选：B．【思路点拨】求出M中不等式的整数解确定出M，求出N中不等式的解集确定出N，找出M 与N的交集即可．【题文】2A．【知识点】运用诱导公式化简求值．C2【答案解析】C 解析：cos（）=cos（670+）=cos=cos （π+）=﹣cos=﹣，故选：C．【思路点拨】原式中角度变形后，利用诱导公式及特殊角的三角函数值计算即可得到结果．【题文】3、已知“0(0)t m m<<>”是“函数()23f x x tx t=--+在区间()0,2上只有一个零点”的充分不必要条件，则m的取值范围是A．()0,2B．(]0,2C．()0,4D．(]0,4【知识点】必要条件、充分条件与充要条件的判断．A2【答案解析】C 解析：对于函数f（x）=﹣x2﹣tx+3t，在区间（0，2）上只有一个零点时，只能△=t2+12t ＞0，即t ＜﹣12，或t ＞0；此时，f （0）f （2）=3t （t ﹣4）＜0，解得0＜t ＜4；∵0＜t ＜m （m ＞0）是函数f （x ）在（0，2）上只有一个零点的充分不必要条件； ∴0＜m ＜4． 故选C ．【思路点拨】先根据函数f （x ）解析式求出该函数在（0，2）上存在零点时t 的取值范围：0＜t ＜4，所以由0＜t ＜m （m ＞0）是f （x ）在（0，2）上存在一个零点的充分不必要条件，得到：0＜m ＜4．【题文】4、已知α为第三象限角，且2sin cos 2,sin 2m m ααα+==，则m 的值为A．【知识点】两角和与差的正弦函数．C5【答案解析】B 解析：把sin α+cos α=2m 两边平方可得1+sin2α=4m2，又sin2α=m2，∴3m2=1，解得m=，又α为第三象限角，∴m=，故选：B【思路点拨】把sin α+cos α=2m 两边平方可得m 的方程，解方程可得m ，结合角的范围可得答案．【题文】5、已知定义在R 上的奇函数()f x ，当0x >时，()2log (21)f x x =+，等于 A ．2log 3 B ．2log 5 C ．1 D ．1-【知识点】函数奇偶性的性质．B4【答案解析】D 解析：∵由f （x ）是定义在R 上的奇函数可得f （﹣x ）=﹣f （x ）， ∴f （﹣）=﹣f （）=﹣=﹣1．故选：D ．【思路点拨】由f （x ）是定义在R 上的奇函数可得f （﹣）=﹣f （），由此可解得f（﹣）的值．【题文】6、已知非零向量,a b ，满足1b =，且b 与b a -的夹角为30，则a是A．[)1,+∞ D 【知识点】平面向量数量积的运算．F3 【答案解析】D 解析：根据题意，作；∴，且∠A=30°；过C 作CD ⊥AB ，垂足为D ，则CD 的长度便是的最小值；在Rt △CDA 中，CA=1，∠A=30°，∴CD=；∴的取值范围是[，+∞）．故选D ．【思路点拨】在空间任取一点C ，分别作，则，并且使∠A=30°．从而便构成一个三角形，从三角形中，便能求出的取值范围．【题文】7，则,,a b c 之间的大小关系是A ．a b c >>B ．b c a >>C ．c a b >>D ．c b a >> 【知识点】对数的运算性质. B7【答案解析】C 解析：a=，b=log9，c=log8，∵=＜，．∴c ＞a ＞b ．故选：C ．【思路点拨】利用对数函数的单调性可得=＜，．即可得出．【题文】8、给出下列命题，其中错误的是 A ．在ABC ∆中，若A B >，则sin sin A B > B ．在锐角ABC ∆中， sin sin A B >C ．把函数sin 2y x =的图象沿x 个单位，可以得到函数cos 2y x =的图象D 最小正周期为π的充要条件是2ω=【知识点】命题的真假判断与应用．A2 【答案解析】D 解析：对于A ．在△ABC 中，若A ＞B ，则a ＞b ，即由正弦定理有sinA ＞sinB ，故A 正确；对于B ．在锐角△ABC 中，A+B ＞，则A ＞﹣B ，由y=sinx 在（0，）上递增，则sinA ＞sin （﹣B ）=cosB ，故B 正确；对于C ．把函数y=sin2x 的图象沿x 轴向左平移个单位，可以得到函数y=sin2（x）=sin（2x）=cos2x的图象，故C正确；对于D．函数y=sinωx+cosωx（ω≠0）=2sin（ωx），最小正周期为π时，ω也可能为﹣2，故D错．故选D．【思路点拨】由正弦定理和三角形中大角对大边，即可判断A；由锐角三角形中，两锐角之和大于90°，运用正弦函数的单调性，即可判断B；运用图象的左右平移，只对自变量x 而言，再由诱导公式，即可判断C；由两角和的正弦公式化简，再由周期公式，即可判断D．【题文】9、已知,a b R∈，函数()tanf x x=在()lng x bx x a=-+在定义域内A【知识点】正切函数的图象. C3【答案解析】D 解析：由函数f（x）=tanx，可得f′（x）=．再根据函数f（x）=tanx在x=﹣处与直线y=ax+b+相切，可得a=f′（﹣）=2．再把切点（﹣，2）代入直线y=ax+b+，可得b=﹣1，∴g（x）=xlnx+1，g′（x）=lnx+1．令g′（x）=lnx+1=0，求得x=，在（0，）上，g′（x）＜0，在（，+∞）上，g′（x）＞0，故g（x）在其定义域（0，+∞）上存在最小值为g （）=2﹣，故选：D．【思路点拨】先求出f′（x）=，再由条件根据导数的几何意义可得a=f′（﹣）=2．再把切点（﹣，2）代入切线方程求得b，可得g（x）解析式．再根据g′（x）的符号，求出g（x）的单调区间，从而求得g（x）的极值．【题文】10、函数()f x是定义在R上的偶函数，且满足()()2f x f x+=，当[]0,1x∈时，()2f x x=，若方程()0(0)ax a f x a+-=>恰有三个不相等的实数根，则实数a的取值范围是A．[]0,2C．()1,2D．[)1,+∞【知识点】抽象函数及其应用．B9【答案解析】A 解析：由f（x+2）=f（x）可得函数f（x）的周期为2，当x∈[0，1]时，f（x）=2x，又f（x）为偶函数，则当x∈[﹣1，0]时，f（x）=﹣2x，由ax+a﹣f（x）=0得f（x）=ax+a，作出y=f（x）和y=ax+a的图象，要使方程ax+a﹣f（x）=0（a＞0）恰有三个不相等的实数根，则由图象可得直线y=ax+a的斜率必须满足kAC＜a＜kAB，由题意可得A（﹣1，0），B（1，2），C（3，2），则kAC==， kAB==1．即有＜a＜1．故选A．【思路点拨】由f（x+2）=f（x）可得函数f（x）的周期为2，当x∈[0，1]时，f（x）=2x，又f（x）为偶函数，则当x∈[﹣1，0]时，f（x）=﹣2x，作出y=f（x）和y=ax+a的图象，要使方程ax+a﹣f（x）=0（a＞0）恰有三个不相等的实数根，则由图象可得有三个交点，即必须满足kAC＜a＜kAB，运用斜率公式即可．第Ⅱ卷二、填空题：本大题共7小题，每小题5分，共35分，把答案填在答案卡中的横线上11【知识点】函数的定义域及其求法．B1【答案解析】(]1,2解析：∵，∴1x2£＜．故答案为：(]1,2．【思路点拨】根据对数的性质，二次根式的性质得不等式组，解出即可．【题文】12【知识点】对数的运算性质．B7【答案解析】25 解析：原式=+lg5lg2+lg22﹣lg2=25+lg2（lg5+lg2）﹣lg2=25．【思路点拨】利用对数的运算法则、lg2+lg5=1即可得出．【题文】13、设α为锐角，若【知识点】两角和与差的正弦函数；两角和与差的余弦函数．C5【答案解析】10解析：根据题意求得sin（α+）=，再根据sin（α﹣）=sin[（α+）﹣]，再利用两角差的正弦公式计算求得结果．【思路点拨】∵α为锐角，cos （）=为正数，∴α+是锐角，sin （α+）=， ∴sin （α﹣）=sin[（α+）﹣]=sin （α+）cos﹣cos （α+）sin=﹣=，故答案为：．【题文】14、设0a b >≥，若()()f a f b =，则()b f a ⋅的取值范围是【知识点】函数的零点；函数的值域．菁B9【答案解析】3,24轹÷ê÷ê滕 解析：由函数，作出其图象如图，因为函数f （x ）在[0，1）和[1，+∞）上都是单调函数，所以若满足a ＞b≥0时f （a ）=f （b ）， 必有b ∈[0，1），a ∈[1，+∞），由图可知，使f （a ）=f （b ）的b ∈[，1），f （a ）∈[，2）．由不等式的可乘积性得：b•f（a ）∈[，2）．故答案为[，2）．【思路点拨】首先作出分段函数的图象，因为给出的分段函数在每一个区间段内都是单调的，那么在a ＞b≥0时，要使f （a ）=f （b ），必然有b ∈[0，1），a ∈[1，+∞），然后通过图象看出使f （a ）=f （b ）的b 与f （a ）的范围，则b•f（a ）的取值范围可求．【题文】15、已知:p 关于x 的方程210x mx ++=有两个不等的负实数根；:q 关于x 的方程244(2)10x m x +-+=的两个实数根，分别在区间()0,2与()2,3内（1）若p ⌝是真命题，则实数m 的取值范围为 （2）若()()p q ⌝∧⌝是真命题，则实数m 的取值范围为 【知识点】复合命题的真假．A2【答案解析】(],2-∞;131,,2128⎛⎤⎡⎤-∞-⋃- ⎥⎢⎥⎝⎦⎣⎦ 解析：（1）若p 为真，则，解得：m ＞2，若￢p 是真命题，则p 是假命题，故实数m 的取值范围是：（﹣∞，2]；（2）对于q ：设f （x ）=4x2+4（m ﹣2）x+1，由q 为真可得，解得：﹣＜m ＜﹣，若q 为假，则m≤﹣或m≥﹣，∴若（￢p ）∧（￢q ）是真命题，则有m≤﹣或﹣m≤2，即m 的范围是：（﹣∞，﹣]∪[﹣，2]；故答案为：（﹣∞，2]，（﹣∞，﹣]∪[﹣，2]．【思路点拨】（1））若p 为真，求出m 的范围，若￢p 是真命题，则p 是假命题，从而得出m 的范围；（2）由q 为真可得m 的范围，若q 为假，求出m 的范围，若（￢p ）∧（￢q ）是真命题，从而求出m 的范围．【题文】16、如图，在矩形ABCD E 为BC 的中点，点F 在边CD上（1）若点F 是CD 的中点，则AE AF ⋅= (2)若2AB AF ⋅=，则AE AF ⋅的值是【知识点】平面向量数量积的运算．菁优F3【答案解析】（1）（1）=（）•（+）=（）•（）=++=×（2+4）+0=3； （2）以A 为坐标原点，AB 所在直线为x 轴，建立如图所示的直角坐标系， 则A （0，0），B （，0），C （，2），D （0，2），E （，1），设F （x ，2），则=（，0），=（x ，2），由•=，x=，则x=1，即F （1，2），=（1﹣，2），=（，1），则•=（，1）•（1﹣，2）=（1﹣）+2=．故答案为：3，【思路点拨】（1）由向量的加法和数乘及数量积的性质，即可求出•；（2）以A 为坐标原点，AB 所在直线为x 轴，建立直角坐标系，写出A ，B ，C ，D ，E 的坐标，设F （x ，2），则=（，0），=（x ，2），由条件即可得到x=1．F （1，2），再由向量的坐标公式和数量积的坐标表示，即可得到所求．【题文】17、在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且2cos 2B a b =+，若ABC ∆的，则ab 的最小值为【知识点】正弦定理．C8 【答案解析】12 解析：在△ABC 中，由条件里用正弦定理可得2sinCcosB=2sinA+sinB=2sin （B+C ）+sinB ，即 2sinCcosB=2sinBcosC+2sinCcosB+sinB ，∴2sinBcosC+sinB=0， ∴cosC=﹣，C=．由于△ABC 的面积为S=ab•sinC=ab=c ，∴c=ab ．再由余弦定理可得c2=a2+b2﹣2ab•cosC，整理可得a2b2=a2+b2+ab≥3ab，当且仅当a=b 时，取等号，∴ab≥12，故答案为：12．【思路点拨】由条件里用正弦定理、两角和的正弦公式求得cosC=﹣，C=．根据△ABC的面积为S=ab•sinC=c ，求得c=ab ．再由余弦定理化简可得a2b2=a2+b2+ab≥3ab，由此求得ab 的最小值．三、解答题：本大题共5小题，满分65分，解答应写出文字说明、证明过程或演算步骤 18、（本小题满分12分） 在ABC∆中，角,,A B C的对边分别为,,a b c，满足()(sin sin )sin sin a b A B c C a B --=-．（1）求角C 的大小；（2，且ABC ∆的面积为【知识点】正弦定理；三角函数中的恒等变换应用．【答案解析】（1）C=．（2）=． 解析：（1）△ABC 中，由（a ﹣b ）（sinA ﹣sinB ）﹣csinC ﹣asinB ， 利用正弦定理可得（a ﹣b ）（a ﹣b ）=c2﹣ab ，即a2+b2﹣c2=ab ．再利用余弦定理可得，cosC==，∴C=．（2）由（1）可得即 a2+b2﹣ab=7 ①，又△ABC 的面积为=，∴ab=6 ②．由①②可得=． 【思路点拨】（1）△ABC 中，由条件利用正弦定理求得 a2+b2﹣c2=ab ．再利用余弦定理求得cosC 的值，可得C 的值．（2）由（1）可得即 a2+b2﹣ab=7 ①，又△ABC的面积为=，可得ab=6 ②．由①②可得的值． 【题文】19、（本小题满分12分）已知向量(sin,cos),(cos,cos) a x x b x x==-．（1）若()b a b⊥-，且cos0x≠，求（2）若()f x a b=⋅，求()f x在【知识点】平面向量数量积的运算；三角函数中的恒等变换应用．菁C7 F3【答案解析】（1）﹣；（2）最大值为﹣1，最小值为﹣﹣．解析：（1）∵向量=（sinx，cosx），=（cosx，﹣cosx ），∴=sinxcosx ﹣cos2x，=2cos2x，∵⊥（﹣），∴（）=0，即有=，∴sinxcosx=3cos2x ，∵cosx≠0，∴sinx=3cosx，即tanx=3．∴sin2x+sin（+2x）=sin2x+cos2x====﹣；（2）f（x ）=•=sinxcosx﹣cos2x=sin2x﹣=（sin2x+cos2x ）﹣=sin（2x﹣）﹣，由于x∈[﹣，0]，则2x﹣∈[﹣，﹣]．则有sin（2x ﹣）∈[﹣1，﹣]，故f（x）∈[﹣﹣，﹣1]，则f（x）在[﹣，0]上的最大值为﹣1，最小值为﹣﹣．【思路点拨】（1）由⊥（﹣），得到（）=0，即有sinxcosx=3cos2x，由cosx≠0，即tanx=3．再由诱导公式和二倍角公式，将所求式子化为含正切的式子，代入即可得到；（2）化简f（x），运用二倍角公式，注意逆用，及两角差的正弦公式，再由x的范围，结合正弦函数的图象和性质，即可得到最值．【题文】20、（本小题满分13分）2014世界园艺博览会在青岛举行，某展销商在此期间销售一种商品，根据市场调查，当每套商品售价为x 元时，销售量可达到150.1x -万套，供货商把该产品的供货价格分为来那个部分，其中固定价格为每套30元，浮动价格与销量（单位：万套）成反比，比例系数为k ，假设不计其它成本，即每套产品销售利润=售价-供货价格（1）若售价为50元时，展销商的总利润为180元，求售价100元时的销售总利润；（2）若10k =，求销售这套商品总利润的函数()f x ，并求()f x 的最大值．【知识点】函数模型的选择与应用．菁B10【答案解析】（1）330（万元）;（2）f （x ）=﹣0.1x2+18x ﹣460，（0＜x ＜150）， 当x=90时，f （x ）取得最大值为350（万元）． 解析：（1）售价为50元时，销量为15﹣0.1×50=10万套， 此时每套供货价格为30+（元），则获得的总利润为10×（50﹣30﹣）=180，解得k=20， ∴售价为100元时，销售总利润为；（15﹣0.1×1000（100﹣30﹣）=330（万元）．（2）由题意可知每套商品的定价x 满足不等式组，即0＜x ＜150，∴f （x ）=[x ﹣（30+）]×（15﹣0.1x ）=﹣0.1x2+18x ﹣460，（0＜x ＜150），∴f′（x ）=﹣0.2x+18，令f′（x ）=0可得x=90，且当0＜x ＜90时，f′（x ）＞0，当90＜x ＜150时，f′（x ）＜0， ∴当x=90时，f （x ）取得最大值为350（万元）． ））]×（R 上的奇函数．（1）若0m >，求()f x 在(,)m m -上递增的充要条件；（2）对任意的实数θ和正实数x恒成立，求实数m 的取值范围．【知识点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值．B12【答案解析】（1）0＜m≤．（2）（﹣∞，0）∪（0，2]．解析：（1）∵函数f（x）=（m≠0）是定义在R上的奇函数．∴f（0）=0，即=0，∴n=0，∴f（x）=，显然f（﹣x）=﹣f（x）成立，故n=0时f（x）为R上的奇函数，∴f′（x）==，∵m＞0，∴﹣m＜0，由f′（x）＞0可得x2﹣2＜0，解得﹣＜x＜，即f（x）的递增区间是（﹣，），由题意只需（﹣m，m）⊆（﹣，），∴0＜m≤，∴f（x）在（﹣m，m）上递增的充要条件是0＜m≤．（2）设g（x）=sinθc0sθ+cos2θ+﹣，∵f（x）≤sinθcosθ+cos2θ+﹣对任意的实数θ和正实数x恒成立，∴f（x）≤g（x）min恒成立，∵g（x）=sinθc0sθ+cos2θ+﹣=sin2θ+﹣=sin2θ+cos2θ+=sin（2θ+）+，∴g（x）min=﹣+=，∴只需f（x）≤，即≤，∵x＞0，∴只需≤，即m≤（x+）恒成立，而（x+）≥×2=2，当且仅当x=时取得最小值2，∴m≤2，又m≠0，∴实数m的取值范围是（﹣∞，0）∪（0，2]．【思路点拨】（1）利用导数判断函数的单调性，由f′（x）＞0解得即可；（2）设g（x）=sinθc0sθ+cos2θ+﹣，由题意得只需f（x）≤g（x）min恒成立，利用三角变换求得g（x）的最小值，列出不等式解得即可．【题文】22、（本小题满分14分）为常数)，在1x=处的切线为20x y+-=．（1）求()y f x=的单调区间；（2，使得对任意的[]1,2t∈上恒有()322f x t t at≥--成立，求实数a的取值范围．【知识点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值．B12 【答案解析】（1）f（x）的递减区间是（0，+∞），无递增区间．（2）[，+∞）．解析：（1）f （x）=+nlnx定义域为（0，+∞），∴f′（x）=﹣+，∴f′（1）=﹣+n=1，把x=1代入x+y﹣2=0可得y=1，∴f（1）==1，∴m=2，n=﹣，∴f（x ）=﹣lnx，f′（x）=﹣﹣，∵x＞0，∴f′（x）＜0，∴f（x）的递减区间是（0，+∞），无递增区间．（2）由（1）可知，f （x）在[，1]上单调递减，∴f（x）在[，1]上的最小值为f（1）=1，∴只需t3﹣t2﹣2at+2≤1，即2a≥t2﹣t+对任意的t∈[，2]恒成立，令g（t）=t2﹣t+则g′（t）=2t﹣1﹣=，∵t∈[，2]，∴2t3﹣t2﹣1=（t﹣1）（2t2+t+1），∴在t∈[，1]上g（t）单调递减，在[1，2]上g（t）单调递增，又g （）=，g （2）=，∴g（t）在[，2]上的最大值是，∴只需2a≥，即a≥，∴实数a的取值范围是[，+∞）．【思路点拨】（1）利用导数的几何意义，求出函数的解析式，利用导数求函数的单调区间；（2）由（1）可知，f（x）在[，1]上单调递减，f（x）在[，1]上的最小值为f（1）=1，只需t3﹣t2﹣2at+2≤1，即2a≥t2﹣t+对任意的t∈[，2]恒成立，令g（t）=t2﹣t+，利用导数求得g（t）的最大值，列出不等式即可求得结论．。

湖北省100所重点中学2012届10月高三联合考试生物试卷考生注意：1．本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共100分。

考试时间90分钟。

2．请将各题答案填在试卷后面的答题卷上。

3．本试卷主要考试内容：(新课标人教版)必修l(60％)；必修2第1～3章(40％)。

第I卷 (选择题共50分)一、选择题(本大题共25小题，每小题2分，共50分。

在每小题给出的四个选项中，只有一项符合题意。

)1．下列能说明原核细胞和真核细胞具有统一性的是A．原核细胞具有与真核细胞相同的染色质B．原核细胞具有与真核细胞相同的细胞分裂方式C．原核细胞具有与真核细胞相同的细胞质D．原核细胞具有与真核细胞相同的细胞膜基本支架2．亲核蛋白是指在细胞核内发挥作用的一类蛋白质。

以下有关亲核蛋白的叙述不正确的是A．亲核蛋白在细胞质中合成B．亲核蛋白进入细胞核的方式与葡萄糖进入红细胞的方式相同C．亲核蛋白可能参与染色体的组成D．与DNA复制有关的酶可能属于亲核蛋白3．下列根据各概念图作出的判断，正确的是A．甲图可以表示植物细胞内储能物质b和糖原a的关系B．若乙中a和b分别代表DNA和RNA，则乙图可以代表原核细胞内的核酸C．丙图可体现出细胞生物膜系统c、核糖体a和线粒体b的关系D．丁图能体现酶c、蛋白质a和核糖核酸b的关系4．关于元素和化合物的叙述，正确的是A．蛋白质的多样性取决于肽键的多样性B．细胞膜上Na+的载体和质粒的基本单位一致C． P是DNA和ATP共有的元素D．ADP审含有两个高能磷酸键5．端粒是存在于真核生物染色体的末端，由DNA序列及其相关的蛋白质所组成的复合体；端粒酶是一种逆转录酶，由蛋白质和RNA构成。

由此可知，属于核糖体、端粒和端粒酶共同点的是A．都只存在于真核细胞中 B．都具有C、H、O、N、P等化学元素C．都与遗传信息的传递无关 D．都含有遗传物质6．下列有关生物膜的叙述，正确的是A．参与细胞膜组成的脂质只有磷脂B．用蛋白酶处理生物膜可改变其组成，不改变其通透性C．抗体的合成和分泌过程都与生物膜有关D．小鼠细胞与人体细胞的细胞膜在一定条件下能够发生融合7．右图是细胞核的结构模式图，下列关于各结构及功能的叙述正确的是A．①是所有生物遗传物质的载体B．所有细胞中核糖体的形成都与②有关C．③属于生物膜系统，把核内物质与细胞质分开D．④是大分子物质如DNA出入细胞核的通道8．用洋葱鳞片叶表皮制备“观察细胞质壁分离实验”的I临时装片，观察细胞的变化。