广义哈密顿系统理论及其应用2版(李继彬,赵晓华,刘正荣著)思维导图

广义哈密顿原理书籍-概述说明以及解释1.引言概述部分介绍了文章的整体内容和目的。

可以根据广义哈密顿原理的概念和研究领域，给出以下内容：概述部分（1.1 概述）：广义哈密顿原理作为经典力学的重要原理之一，是描述物理系统运动的一种数学工具。

该原理由数学家和物理学家威廉·哈密顿于1834年首次提出，并在之后的几个世纪里得到了广泛的应用和发展。

本文旨在探讨广义哈密顿原理的基本概念、历史发展以及应用领域，并深入阐述其在物理学研究中的重要性。

通过对广义哈密顿原理的深入理解和探索，有助于我们更好地理解物理系统的运动规律和宏观现象的涌现。

在本文的正文部分，我们将首先介绍广义哈密顿原理的定义，包括其数学形式和基本假设。

接着，我们将回顾广义哈密顿原理的历史发展，了解其在物理学研究中的重要里程碑和贡献。

然后，我们将探讨广义哈密顿原理的应用领域，包括经典力学、量子力学、相对论以及其他学科领域中的应用案例。

最后，我们将总结广义哈密顿原理的关键要点，并展望其未来的发展方向。

通过本文的研究，我们将深入了解广义哈密顿原理的数学和物理背景，掌握其在物理学中的重要性和应用方法。

同时，我们也将思考广义哈密顿原理对于理解和解释自然界中各种现象的意义和启示。

总之，本文将为读者提供一份关于广义哈密顿原理的综合介绍和分析，希望能对物理学和科学研究的发展做出一定的贡献。

文章结构是撰写一篇长文的基本框架，它有助于读者更好地理解文章的内容和思路。

本文按照以下结构来组织：一、引言部分1.1 概述：对广义哈密顿原理进行简要介绍，包括其定义、起源和重要性。

1.2 文章结构：本节内容1.3 目的：说明本文撰写的目的，即通过介绍广义哈密顿原理的书籍，向读者推荐一些值得阅读的文献，帮助读者更好地理解和应用广义哈密顿原理。

二、正文部分2.1 广义哈密顿原理的定义：详细介绍广义哈密顿原理的概念和基本原理，包括其在物理学领域的应用以及数学表达方式等方面。

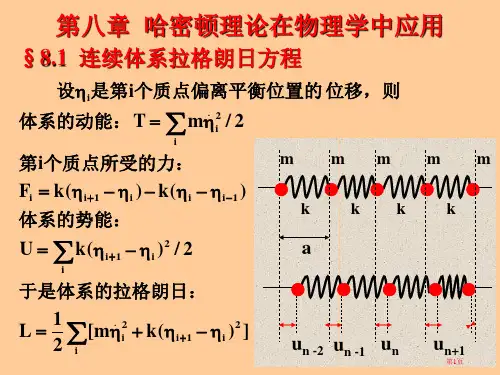
课程名称：现代计算力学课程编号：课程类型：非学位课考核方式：考试、考查学科专业：结构工程年级：研一姓名：邢晨鹏学号： 10076130065河北工程大学 2013～2014 学年第二学期研究生课程论文报告对偶求解体系及其精细积分法学院：土木工程学院专业：结构工程姓名：邢晨鹏学号： 10076130065摘要：本文主要介绍了哈密顿体系的求解步骤，将哈密顿求解体系推广应用于弹性地基上的铁摩辛柯梁问题。

首先导出了梁的总是能，然后采用拉格朗日函数导出拉格朗日方程，最后提出哈密顿函数及哈密顿正则方程。

弹性地基上的梁的哈密顿理论成果将为研究铁摩辛柯里梁解析解和有限元解提供新的有效工具。

关键词：哈密顿求解体系；拉格朗日方程；对偶方程；变分原理；精细积分法；正则方程Abstract:This paper mainly introduces the solution procedure of Hamiltonian system, the Hamiltonian solution system is applied to the elastic foundation on elastic Timoshenko problem. Firstly deduced beam can always, then the Lagrange function to derive the Lagrange equation , the final Hamiltonian and Hamiltonian canonicalequation is proposed. Hamiltonian theory . Hamiltonian theory of beam on elastic foundation for the study of the Timoshenko beam analytical solution provides a new effective tool and finite element solution 。

哈密顿量和广义能量1.引言1.1 概述概述部分将介绍哈密顿量和广义能量的概念，并提供一些背景信息。

哈密顿量是物理学中一个重要的概念，用来描述系统的能量和运动的演化。

广义能量则是与哈密顿量密切相关的一个概念，它更加普遍地描述系统的能量和动力学性质。

在物理学中，哈密顿量是描述系统所有位置和动量的函数，它是描述经典力学和量子力学中系统演化的核心数学工具之一。

哈密顿量的求解可以帮助我们理解物理系统的行为，并在广泛的领域中找到应用，如粒子物理学、动力学、电磁学等。

通过哈密顿量，我们可以获得系统的能量、守恒定律、运动方程等重要信息。

然而，哈密顿量的应用不仅限于经典力学和量子力学，它在相对论物理中也扮演着重要的角色。

相对论物理中的广义能量概念将在本文中详细讨论。

广义能量是描述系统的能量和动力学行为的理论框架，它包含了相对论效应和引力的影响，可以更准确地描述引力场中物体的运动和能量变化。

本文将探讨哈密顿量和广义能量的定义、性质以及它们在物理学中的应用。

我们将详细讨论哈密顿量的意义以及与系统能量和运动之间的关系。

同时，我们还将介绍广义能量的概念和背景，并探讨它在相对论物理中的应用。

通过对哈密顿量和广义能量的分析，我们可以更深入地理解系统的动力学性质和能量变化规律。

同时，我们也可以展望一些未来对哈密顿量和广义能量的研究方向，以推动物理学领域的进一步发展。

随后的正文将细分为2.1节和2.2节，分别讨论哈密顿量和广义能量的定义、性质以及应用。

最后，在结论部分，我们将总结哈密顿量和广义能量的关系，并展望未来对它们的研究方向。

通过文章的阐述，我们希望读者能够更加深入地理解和应用哈密顿量和广义能量在物理学中的重要性。

1.2文章结构1.2 文章结构本文分为引言、正文和结论三个部分。

具体结构如下：引言部分将对整个文章的背景和目的进行概述，确立研究的重要性和必要性。

首先，将简要介绍哈密顿量和广义能量的概念，阐明它们在物理学和相关领域的重要性。

一类4维Lotka-Volerra系统的Hamilton结构及动力学赵晓华;戴灿华【摘要】It was studied a four dimensional Lotka-Volterra (LV) system with Hamiltonian structure. The results showed that the LV system had at least three different families of periodic solutions for generic parameters , and it was nonintegrable for small a23 ≠0 and Hamiltonian chaos might occur.%运用动力系统的方法研究了一类具有Hamilton结构的4维保守型Lotka-Volterra系统.结果显示:这类系统具有很复杂的动力学性质,相空间包含至少3族周期轨道；对一般参数,这个系统是不可积的,会出现Hamilton混沌.【期刊名称】《浙江师范大学学报（自然科学版）》【年(卷),期】2011(034)003【总页数】5页(P241-245)【关键词】Lotka-Volterra系统;Hamilton结构;周期解;Lyapunov指数;Hamilton混沌【作者】赵晓华;戴灿华【作者单位】浙江师范大学数理与信息工程学院,浙江金华 321004;浙江师范大学数理与信息工程学院,浙江金华 321004【正文语种】中文【中图分类】O19;O75.140 引言本文涉及的Lotka-Volterra系统是指下面的常微分方程组:式(1)中:xj表示第j个物种的种群密度;A=(ajk)称为作用矩阵，表示物种间的相互作用关系;εj是与环境相关的参数．自19世纪20年代Lotka和Volterra分别在研究化学反应和生物问题时提出上述Lotka-Volterra(LV)系统以来，方程组(1)已经被广泛应用于物理、化学、生物、动态博弈论、经济和其他的社会科学中，成为应用数学领域中一个重要的微分方程模型，还被应用于许多热门学科，如神经网络、生物反应、细胞演化和病毒传播等［1-6］，LV系统受到数学及其他学科领域的关注越来越多．在过去的80多年里，对LV系统的理论及应用研究成果大量涌现［7-8］．但是，除了2维的Lotka-Volterra系统的动力学性质和一些特殊类型的高维Lotka-Volterra系统已分析清楚外，一般的高维Lotka-Volterra系统的动力学性质还远远没有弄清楚，有待深入研究．研究表明，Lotka-Volterra系统的动力学性质和它的作用矩阵的代数性质有着密切的关系．根据作用矩阵A的不同性质，Lotka-Volterra系统可分为3类［5］(定义1)．定义1 具有作用矩阵A=(aij)的Lotka-Volterra系统称为:1)合作型(或竞争型)，如果对任意i≠j，aij≥0(aij≤0);2)保守型，如果存在一个正对角矩阵D＞0，使得AD是反对称的;3)耗散型，如果存在一个正对角矩阵D＞0，使得在二次型意义下AD≤0．对于耗散型系统，考虑到模型的实际应用，更值得研究的是稳定耗散系统，即作用矩阵A及其对非零元素的小扰动所得的矩阵˜A均为耗散型．以往的研究主要涉及合作(或竞争)型LV系统，对保守型和耗散型系统的研究相对较少［5-7］．其中特别值得注意的是1998年Duarte等在文献［5］中对这两类系统的研究，他们证明:保守型LV系统若存在正平衡点，则它具有广义Hamilton 结构，可以表示为Poisson流形上的广义Hamilton系统;而具有正平衡点的稳定耗散LV系统存在一个整体吸引集，其上的动力学控制方程是一个较低维数的具有广义Hamilton结构的保守型LV系统．关于Hamilton和广义Hamilton系统的相关知识可参阅文献［9-10］．根据Duarte等的这些结论可以得出，若这个吸引集是单点集，则原LV系统是全局渐进稳定的;若吸引集不是单点集，则需进一步研究吸引集上的子系统的轨道性质．因此，为了弄清稳定耗散系统在吸引集上的动力学性质，本质上就是要研究具有广义Hamilton结构的保守型LV系统的动力学性质．本文研究了一类具有广义Hamilton结构的4维保守型LV系统，这个系统包含至少3族周期轨道，而对一般的参数是不可积的，并且会出现Hamilton混沌．进而也表明:一般而言，稳定耗散LV系统吸引集的结构可能非常丰富而复杂，值得深入系统地研究．1 Hamilton结构及平衡点稳定性分析本文考虑如下的4维Lotka-Volterra系统:对应的作用矩阵为式(3)中:已被标出的元素aij≠0;aijaji＜0．考虑到系统(2)的特殊结构及实际应用背景，只对不变区域在假设条件aijaji＜0下，系统(2)实际上是一个保守型系统，因为可取对角矩阵D=diag(d1，d2，d3，d4)的对角元素为则可使DA为反对称矩阵．进一步，容易验证变换xj→djxj保持系统(2)的形式不变，但作用矩阵变为DA，为反对称矩阵．因此，不失一般性，直接假定系统(2)的作用矩阵(3)满足以下条件:容易验证，若参数 bj(j=1，2，3，4)满足条件则系统(2)存在唯一正平衡点另一方面，在光滑函数空间C∞(R4+)上定义Poisson括号{·，·}为式(8)中，A=(ajk)是满足条件式(5)的系统(2)的作用矩阵．根据辛流形及其上定义的Hamilton系统的理论［9］，直接验证可知{R4+，{·，·}}构成一个4维辛流形，并且有命题1成立．命题1 在假设式(5)和式(6)成立的情况下，LV系统(2)是4维辛流形{R4+，{·，·}}上的 Hamilton系统，可将系统(2)改写为如下Hamilton形式:作为Hamilton系统的重要性质之一，Hamilton函数H(x)是LV系统(2)的首次积分，即H沿着系统DH(q)=0，并且Hess矩阵D2H(q)正定，从而根据Dirichlet稳定定理［10］可证得命题2．命题2 在假设式(5)和式(6)成立的条件下，LV系统(2)的正平衡点q是Lyapunov稳定的．最后，利用 Morse引理［11］得:对任意 h＞0，水平集Mh={x∈R4+|H(x)-H(q)=h}拓扑等价于一个3维球面S3．2 周期轨道为进一步研究系统(2)的周期解，先介绍下面的Lyapunov中心定理［10］．引理1(Lyapunov中心定理) 设(M，Ω)是一个2n维辛流形，XH是定义在M上的Hamilton向量数，则存在XH的一个过平衡点q的2维不变流形，其上充满围绕q的周期轨道，它们的周期随着轨道逼对于系统(2)的唯一正平衡点q，简单计算即可得到其相应的特征方程为式(10)中:由式(5)和式(6)知 P ＞0，Q ＞0，Δ =P2-4Q ＞0．于是可得命题3．命题3 在式(5)和式(6)成立的条件下，系统(2)在正平衡点q处的特征方程(10)有2对简单共轭纯虚根，分别为:由上述命题看出，在式(5)和式(6)成立的条件题2，可以得定理1和定理2．定理1 在式(5)和式(6)成立的条件下，系统(2)至少存在1个过平衡点q的2维不变子流形Π1，数，则存在另一个过q的2维不变流形Π2，其上充满围绕q的周期解，随着这些周期解收缩到q，其相应系统(2)除了以上周期解外，还可能存在其他周期解．容易验证，若系统(2)中的a23=0，但式(5)和式(6)中的其他式子仍满足，则系统变为2个独立的2维LV系统:此时系统是可积的，并有2个独立的首次积分:而且在平衡点q处的特征值为2对简单纯虚根:因此，系统(12)的轨道由2个子系统的轨道(均为周期轨道)组合而成，分布于I1(x)和I2(x)确定的水平集上，这个水平集由轨道的初值确定，拓扑等价于2维环面S1×S1，仅当2个子系统解的周期之比为有理数时，对应的4维系统(12)的解才是周期解，否则为拟周期环面解．特别地，若(φ1(t，I1)，φ2(t，I1))和(φ3(t，I2)，φ4(t，I2))分别是 2 个子系统的周期解，则(φ1(t，I1)，φ2(t，I1)，q3，q4)和(q1，q2，φ1(t，I2)，φ2(t，，I2))就是对应 4 维系统(12)的 2 个周期解，而且易证它们都是Hamilton系统(2)在参数a23=0时的椭圆型周期解．根据Hamilton系统的性质，当a23≠0充分小时，Hamilton系统(2)仍然存在2个与它们对应的周期解．定理2 在式(5)和式(6)成立的条件下，当a23≠0充分小时，系统(2)存在2族分别对应于(φ1(t，，I1)，φ2(t，I1)，q3，q4)和(q1，q2，φ1(t，I2)，φ2(t，，I2))的周期解．3 不可积性与Hamilton混沌根据Hamilton系统中的Liouville完全可积性定义［9-10］，若4维系统(2)还存在一个独立于Hamilton函数H(x)的首次积分I(x)，则它的解均在H(x)和I(x)确定的水平集上，而这个水平集是紧致的(H(x)的水平集拓扑等价于3维球面)．故由完全可积性定理知，该水平集拓扑等价于2维不变环面，其上若存在周期解，则必属于定理1中那两族之一．另一方面，对充分小的a23≠0，系统(2)在式(5)和式(6)成立的条件下至少有3族非退化的周期轨道．因此，可得定理3．定理3 对充分小的a23≠0，系统(2)在Liouville意义下是不可积的．下面用Lyapunov指数来数值论证系统(2)是否出现Hamilton混沌．Lyapunov指数是反映一个动力系统是否存在混沌的主要工具［12］．若所考虑的动力系统存在正的Lyapunov指数，则可认为系统是混沌的．对于系统(2)，若取参数a12=a23=a34=1，b1=b3=-1，b2=b4=1，则用数学软件Maple计算该系统的最大Lyapunov指数，结果如图1所示．图1 Lyaounov指数从图1可看到，系统(2)的4个Lyapunov指数中有2个为0，另外2个Lyapunov指数为±0．445．因此，此系统是混沌的．参考文献:［1］Hofbauer J，Sigmund K．Evolutionary games and population dynamics［M］．Cambridge:Cambridge University Press，1998．［2］Xia Yonghui．New results on the global asymptotic stability of a Lotka-Volterra system［J］．Appl Math Comput，2011，36(1/2):117-128．［3］Svirezhev Y M．Nonlinearities in mathematical ecology:Phenomena and models:Would we live in Volterra's world?［J］．Ecological Modelling，2008，216(2):89-101．［4］Upadhyay R K．Observability of chaos and cycles in ecological systems:Lessons from predator-prey models［J］．International Journal of Bifurcation and Chaos，2009，19(10):3169-3234．［5］Duarte P，Fernandes R L，Oliva W M．Dynamics of the attractor in the Lotka-Volterra equations［J］．Journal of Differential Equations，1998，149(1):143-169．［6］Zhao Xiaohua，Luo Jigui．Classification and dynamics of stably dissipative Lotka-Volterra systems［J］．International Journal of Nonlinear Mechanics，2010，45(6):603-607．［7］赵晓华，吴红颖．保守型Lotka-Volterra系统的Hamilton结构与周期解［J］．浙江师范大学学报:自然科学版，2007，30(3):246-250．［8］Picard G，Johnstone T W．Instabillity cascades，Lotka-Volterra population equations，and Hamilton chaos［J］．Physical Review Letters，1982，48(23):1610-1613．［9］李继彬，赵晓华，刘正荣．广义哈密尔顿系统理论及其应用［M］．2版．北京:科学出版社，2007．［10］Meyer K R，Hall G R，Offin D．Introduction to Hamiltonian dynamical systems and the N-body problem［M］．2nd ed．NewYork:Springer，2009．［11］Milnor J．Morse theory［M］．New Jersey:Princeton University Press，1969．［12］Ott E．Chaos in dynamical systems［M］．2nd ed．Cambridge:Cambridge University Press，2002．。

广义动量定理与系统思考——战争、管理学与经济学通论第五篇管理学通论2.8 广义速度V与管理理论广义动量定理Fαt=MV中，增加广义速度V，可以增加成果MV。

有三大生产方法可以增加广义速度V，分别为福特的流水线生产，大野耐一的丰田生产方式和高德拉特的TOC制约理论。

加快产出速度V是工厂的主要目标，高德拉特说：“加快流动（或缩短生产所需时间）是工厂的主要目标。

”；大野耐一说：“我们所做的，其实就是注意从接到顾客订单到向顾客收帐这期间的作业时间，由此剔除不能创造价值的浪费，以缩短作业时间。

”三种生产理论是广义动量定理与系统思考的结合，广义动量定理用来产生成果MV，系统思考用来指导何时产生，产生多少，产生什么样的成果才能使系统的产出最大化。

在三大生产理论中，以广义动量定理所阐述的工业工程来增加成果，以系统思考的负反馈来指导生产。

2.8.1 福特的流水线生产流水线生产，指劳动对象按一定的工艺路线和统一的生产速度，连续不断地通过各个工作地，按顺序地进行加工并生产出产品的一种生产组织形式。

它是对象专业化组织形式的进一步发展，是劳动分工较细、生产效率较高的一种生产组织形式。

亨利•福特(Henry Ford)于1913年在密歇根州的Highland Park，建立的生产系统。

1913年，福特应用创新理念和反向思维逻辑提出在汽车组装中，汽车底盘在传送带上以一定速度从一端向另一端前行。

前行中，逐步装上发动机，操空系统，车厢，方向盘，仪表，车灯，车窗玻璃、车轮，一辆完整的车组装成了。

在手工生产时代，每装配一辆汽车要728个人工小时，而福特的简化设计，标准部件的T型车把这缩短为12.5个小时。

进入汽车行业的第十二年，亨利福特终于实现了他的梦想，他的流水线的生产速度已达到了每分钟一辆车的水平，五年后又把进一步缩短到每十秒钟一辆车，生产效率提高了4488倍。

流水线是怎样提高速度的？流水线把生产工序被分割成一个个的子过程，每个子过程可以和其他子过程并行运作提高速度。