用A算法解决十五数码问题
- 格式：docx
- 大小：31.01 KB
- 文档页数：5
下载文档原格式
合集下载
a算法八数码问题例题
a算法八数码问题例题八数码问题是一个经典的搜索问题，其中有一个3×3的格子，其中包含了一些数字（通常是1到8），以及一个空白格。
目标是使用最少的步骤将格子中的数字排列成给定的目标顺序。
每个步骤可以是以下三种操作之一：1. 上下移动（将行中的某个数字上移或下移）2. 左右移动（将列中的某个数字左移或右移）3. 旋转（以中心为中心旋转整个格子）下面是一个使用A算法解决八数码问题的例子：假设初始状态如下：```markdown4 1 2 756 3 8 05 0 3 2 4 167 86 7 5 8 3 4 2 1 0```目标状态如下：```markdown1 2 3 4 5 6 7 8 00 3 6 7 4 5 8 1 27 8 5 6 1 2 3 4 0```下面是使用A算法解决这个问题的步骤：1. 首先，我们需要构建一个优先级队列（例如最小堆），用于存储所有可能的移动。
在这个例子中，每个移动都有一个成本和优先级。
成本是从当前状态到目标状态的最短路径长度，优先级是当前状态到目标状态的H启发式估计。
H启发式估计通常是当前状态和目标状态之间的曼哈顿距离。
2. 从队列中取出优先级最高（即成本最低）的移动。
在这个例子中，初始状态的移动是"上下移动"。
3. 应用这个移动，并更新所有相关状态的成本和优先级。
在这个例子中，我们将第一行向下移动一格。
然后，我们需要重新评估所有可能的状态，并更新优先级队列。
4. 在更新优先级队列后，我们需要检查是否已经达到目标状态。
如果已经达到目标状态，则算法结束。
否则，我们重复步骤2和步骤3，直到达到目标状态。
5. 在这个例子中，我们需要进行多次上下移动、左右移动和旋转，才能将数字排列成目标顺序。
每次应用移动后，都需要重新评估所有可能的状态，并更新优先级队列。
a星算法求解八数码问题python
a星算法求解八数码问题python一、介绍八数码问题是一种经典的智力游戏，也是人工智能领域中的经典问题之一。
在这个问题中，有一个3×3的棋盘，上面摆着1至8这8个数字和一个空格，初始状态和目标状态都已知。
要求通过移动数字，将初始状态变换成目标状态。
其中空格可以和相邻的数字交换位置。
为了解决这个问题，我们可以使用A*算法。
本文将详细介绍如何用Python实现A*算法来求解八数码问题。
二、A*算法简介A*算法是一种启发式搜索算法，常用于寻找最短路径或最优解等问题。
它基于Dijkstra算法，并加入了启发式函数来加速搜索过程。
在A*算法中，每个节点都有两个估价值：g值和h值。
g值表示从起点到该节点的实际代价，h值表示从该节点到目标节点的估计代价。
启发式函数f(n) = g(n) + h(n) 表示从起点到目标节点的估计总代价。
A*算法采用优先队列来保存待扩展的节点，并按照f(n)值从小到大排序。
每次取出队头元素进行扩展，并将扩展出来的新节点按照f(n)值插入队列中。
当扩展出目标节点时，算法结束。
三、八数码问题的状态表示在八数码问题中，每个状态都可以表示为一个3×3的矩阵。
我们可以用一个一维数组来表示这个矩阵，其中0表示空格。
例如，初始状态可以表示为[2, 8, 3, 1, 6, 4, 7, 0, 5]，目标状态可以表示为[1, 2, 3, 8, 0, 4, 7, 6, 5]。
四、A*算法求解八数码问题的步骤1.将初始状态加入优先队列中，并设置g值和h值为0。
2.从队头取出一个节点进行扩展。
如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。
3.对于每个新节点，计算g值和h值，并更新f(n)值。
如果该节点已经在优先队列中，则更新其估价值；否则，将其加入优先队列中。
4.重复第2步至第3步直到搜索结束。
五、Python实现以下是用Python实现A*算法求解八数码问题的代码：```import heapqimport copy# 目标状态goal_state = [1,2,3,8,0,4,7,6,5]# 启发式函数：曼哈顿距离def h(state):distance = 0for i in range(9):if state[i] == 0:continuerow = i // 3col = i % 3goal_row = (state[i]-1) // 3goal_col = (state[i]-1) % 3distance += abs(row - goal_row) + abs(col - goal_col)return distance# A*算法def A_star(start_state):# 初始化优先队列和已访问集合queue = []visited = set()# 将初始状态加入优先队列中，并设置g值和h值为0heapq.heappush(queue, (h(start_state), start_state, 0))while queue:# 取出队头元素进行扩展f, state, g = heapq.heappop(queue)# 如果该节点是目标节点，则搜索结束；否则，将扩展出来的新节点加入优先队列中。
基于启发式搜索算法A星解决八数码问题
//定义算法中用到的链表，图，树的节点的结构。 struct Node {
int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树，该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表，该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表，该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表，该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表，表头为 head_b，将 bestNode 所指节点的不是前驱节点的后继 节点，链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点，将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp，并从
int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树，该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表，该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表，该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表，该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表，表头为 head_b，将 bestNode 所指节点的不是前驱节点的后继 节点，链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点，将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp，并从
A-star-算法-八数码问题-C++-报告+代码+详细注释1
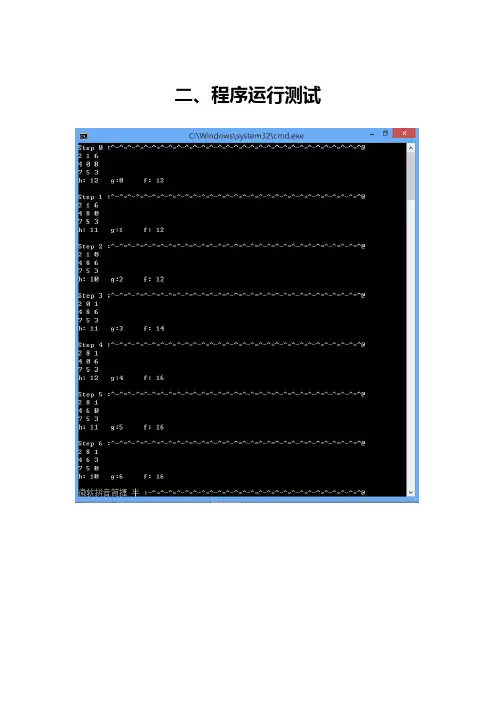
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小, 该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH（state & st）;countH函数功能是计算st状态的h值。
2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置（位置 = 行下标 * 3 + 列下标）。
2.3f（state * p）;f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。
2.6search(state & start)；在open表不为空时, 按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。
确定某方向可走后, 空格移动一步, 生成状态p’。
2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据；检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。
2.8重复的执行这个过程, 直到某状态的h值为零。
2.9dump_solution(state * q)；在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等（对应位置元素相等）, 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。
A算法
6
7
2．局部择优搜索
在局部择优搜索中，每当需要扩展节点时，总是从刚生成的子节 点中选择一个估价函数值最小的节点进行扩展。其搜索过程可描 述如下：
(1)把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)； (2)如果Open表为空，则问题无解，失败退出； (3)把Open表的第一个节点取出放入Closed表，并记该节点为n； (4)考察节点n是否为目标节点。若是，则找到了问题的解，成功
10
假设f*(n)为从初始节点S0出发，约束经过节点n到达 目标节点的最小代价值。估价函数f(n)则是f*(n)的估 计值。显然，f*(n)应由以下两部分所组成：一部分是 从初始节点S0到节点n的最小代价，记为g*(n)；另一 部分是从节点n到目标节点的最小代价，记为h*(n)， 当问题有多个目标节点时，应选取其中代价最小的一 个。因此有
2
1. 全局择优搜索
在全局择优搜索中，每当需要扩展节点时，总是从Open表的所有节点中 选择一个估价函数值最小的节点进行扩展。其搜索过程可能描述如下：
（1）把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)； （2）如果Open表为空，则问题无解，失败退出； （3）把Open表的第一个节点取出放入Closed表，并记该节点为n； （4）考察节点n是否为目标节点。若是，则找到了问题的解，成功退出； （5）若节点n不可扩展，则转到第(2)步； （6）扩展节点n，生成子节点ni(i=1,2,……)，计算每一个子节点的估价
26
定理4
设有两个A*算法A1*和A2*，它们有
A1*：f1(n)=g1(n)+h1(n)
A2*：f2(n)=g2(n)+h2(n)
7
2．局部择优搜索
在局部择优搜索中，每当需要扩展节点时，总是从刚生成的子节 点中选择一个估价函数值最小的节点进行扩展。其搜索过程可描 述如下：
(1)把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)； (2)如果Open表为空，则问题无解，失败退出； (3)把Open表的第一个节点取出放入Closed表，并记该节点为n； (4)考察节点n是否为目标节点。若是，则找到了问题的解，成功
10
假设f*(n)为从初始节点S0出发，约束经过节点n到达 目标节点的最小代价值。估价函数f(n)则是f*(n)的估 计值。显然，f*(n)应由以下两部分所组成：一部分是 从初始节点S0到节点n的最小代价，记为g*(n)；另一 部分是从节点n到目标节点的最小代价，记为h*(n)， 当问题有多个目标节点时，应选取其中代价最小的一 个。因此有
2
1. 全局择优搜索
在全局择优搜索中，每当需要扩展节点时，总是从Open表的所有节点中 选择一个估价函数值最小的节点进行扩展。其搜索过程可能描述如下：
（1）把初始节点S0放入Open表中，f(S0)=g(S0)+h(S0)； （2）如果Open表为空，则问题无解，失败退出； （3）把Open表的第一个节点取出放入Closed表，并记该节点为n； （4）考察节点n是否为目标节点。若是，则找到了问题的解，成功退出； （5）若节点n不可扩展，则转到第(2)步； （6）扩展节点n，生成子节点ni(i=1,2,……)，计算每一个子节点的估价
26
定理4
设有两个A*算法A1*和A2*，它们有
A1*：f1(n)=g1(n)+h1(n)
A2*：f2(n)=g2(n)+h2(n)
a算法求解八数码问题 实验报告
题目: a算法求解八数码问题实验报告目录1. 实验目的2. 实验设计3. 实验过程4. 实验结果5. 实验分析6. 实验总结1. 实验目的本实验旨在通过实验验证a算法在求解八数码问题时的效果，并对其进行分析和总结。
2. 实验设计a算法是一种启发式搜索算法，主要用于在图形搜索和有向图中找到最短路径。
在本实验中，我们将使用a算法来解决八数码问题，即在3x3的九宫格中，给定一个初始状态和一个目标状态，通过移动数字的方式将初始状态转变为目标状态。
具体的实验设计如下：1) 实验工具：我们将使用编程语言来实现a算法，并结合九宫格的数据结构来解决八数码问题。
2) 实验流程：我们将设计一个初始状态和一个目标状态，然后通过a 算法来求解初始状态到目标状态的最短路径。
在求解的过程中，我们将记录下每一步的状态变化和移动路径。
3. 实验过程我们在编程语言中实现了a算法，并用于求解八数码问题。
具体的实验过程如下：1) 初始状态和目标状态的设计：我们设计了一个初始状态和一个目标状态，分别为：初始状态：1 2 34 5 67 8 0目标状态：1 2 38 0 42) a算法求解：我们通过a算法来求解初始状态到目标状态的最短路径，并记录下每一步的状态变化和移动路径。
3) 实验结果在实验中，我们成功求解出了初始状态到目标状态的最短路径，并记录下了每一步的状态变化和移动路径。
具体的实验结果如下：初始状态：1 2 34 5 67 8 0目标状态：1 2 38 0 47 6 5求解路径：1. 上移1 2 37 8 62. 左移1 2 3 4 0 5 7 8 63. 下移1 2 3 4 8 5 7 0 64. 右移1 2 3 4 8 5 0 7 65. 上移1 2 3 0 8 5 4 7 61 2 38 0 54 7 67. 下移1 2 38 7 54 0 68. 右移1 2 38 7 54 6 0共计8步，成功从初始状态到目标状态的最短路径。
15数码问题解法
15数码问题解法The 15-puzzle is a classic sliding puzzle that consists of 15 numbered tiles on a 4x4 grid with one empty space. The goal is to arrange the tiles in numerical order by sliding them into the empty space. It might seem like a simple task, but the puzzle can be quite challenging and require strategic thinking to solve.15数码问题是经典的滑动拼图，由4x4网格上的15个编号瓦片和一个空格组成。
目标是通过将瓦片滑入空格来按数字顺序排列瓦片。
这个谜题看起来可能很简单，但是解决这个问题可能会很有挑战性，需要策略性的思维来解决。
One approach to solving the 15-puzzle involves creating a solving strategy that prioritizes certain moves over others. By identifying patterns and common sequences of moves, you can improve your efficiency in solving the puzzle. This can help you avoid getting stuck in dead-end positions and find the most efficient path to completing the puzzle.解决15数码问题的一种方法是创建一个解决策略，优先考虑某些移动而不是其他移动。
用A算法解决十五数码问题
精心整理一、15数码问题的描述及其状态空间法表示（1）15数码问题描述15数码问题又叫移棋盘问题，是人工智能中的一个经典问题。
所谓的15数码问题：就是在一个4×4的16宫格棋盘上，摆放有15个将牌，每一个将牌都刻有1～15中的某一个数码。
棋盘中留有一个空格，允许其周围的某一个将牌向空格移动，这样通过移动将牌就可以不断改变将牌的布局。
这种求解的问题是：给定一种初始的将牌布局或结构(称初始状态)和一个目标布局(称目标状态)，问如何移动数码，实现从初始状态到目标状态的转变，如图1所示。
问题的实质就是寻找一个合法的目标状态集合。
十五数码的状态空间法：初始状态S[4][4]={5,12,11,4,13,6,3,10,14,2,7,9,1,15,0,8}；(0表示空格)目标状态G[4][4]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0}；操作符集合F={空格上移，空格下移，空格左移，空格右移}状态空间的一个解：是一个有限的操作算子序列，它使初始状态转化为目标状态：S0-f1->S1-f2->...fk->G。
二、A*算法的基本原理、算法步骤、流程图（1）A*算法基本原理A*算法是一种有序搜索算法，其特点在于对评价函数的定义上。
对于一般的有序搜索，总是选择f值最小的节点作为扩展节点。
因此，f是根据需要找到一条最小代价路径的观点来估算节点的，可考虑将每个节点n的估价函数值分解为两个分量：从起始节点到节点n的最小代价路径的代价与从节点n到目标节点的最小代价路径的代价之和，也就是说f(n)是约束通过节点n的一条最小代价路径的代价的一个估计。
再定义一个函数f*，使得在任意一个节点n上的函数值f*(n)就是从节点S到节点n的一条最佳路径的实际代价加上从节点n到目标节点的一条最佳路径的代价之和，即：***在第7步中，如果搜索过程发现一条路径到达一个节点的代价比现存的路径代价低，就要重定向指向该节点的指针。
状态空间搜索实验报告
一、实验目的1. 理解状态空间搜索的基本概念和原理。
2. 掌握状态空间搜索方法在解决问题中的应用。
3. 比较不同搜索算法的优缺点，提高搜索效率。
二、实验内容本次实验主要涉及以下内容：1. 状态空间搜索的基本概念和原理。
2. 常用搜索算法：深度优先搜索（DFS）、广度优先搜索（BFS）、A搜索算法。
3. 状态空间搜索在解决实际问题时（如八数码问题、十五数码难题）的应用。
三、实验步骤1. 理解状态空间搜索的基本概念和原理。
状态空间搜索是一种求解问题的方法，将问题求解过程表示为从初始状态到目标状态的搜索过程。
状态空间搜索主要包括以下几个步骤：（1）确定问题的初始状态；（2）确定问题的目标状态；（3）定义状态空间，包括所有可能的状态和状态之间的转换关系；（4）确定搜索策略，选择合适的搜索算法。
2. 学习并实现常用搜索算法。
（1）深度优先搜索（DFS）：按照一定的顺序前查找完一个分支，再查找另一个分支，直至找到目标状态。
（2）广度优先搜索（BFS）：从初始状态一层一层向下搜索，直至找到目标状态。
（3）A搜索算法：结合启发式信息和代价函数，在搜索过程中优先考虑估计距离目标状态较近的状态。
3. 应用状态空间搜索解决实际问题。
以八数码问题为例，实现以下步骤：（1）定义问题状态：将8个数码排成一行，空白格用0表示。
（2）确定操作符集合：包括上下左右四个方向移动空白格。
（3）建立状态空间：根据初始状态，通过操作符集合生成所有可能的状态。
（4）选择搜索算法：实现DFS、BFS和A搜索算法，分别求解八数码问题。
4. 比较不同搜索算法的优缺点。
通过实验结果，分析DFS、BFS和A搜索算法在解决八数码问题时的搜索效率、空间复杂度和时间复杂度。
四、实验结果与分析1. 八数码问题的初始状态和目标状态如下：初始状态：1 2 3 4 5 6 7 8 0目标状态：0 1 2 3 4 5 6 7 82. 实验结果如下：（1）深度优先搜索（DFS）：- 找到目标状态的搜索路径：10步- 空间复杂度：递归调用栈的深度，约为8层- 时间复杂度：由于DFS搜索过程可能遍历大量无效路径，因此时间复杂度较高（2）广度优先搜索（BFS）：- 找到目标状态的搜索路径：31步- 空间复杂度：队列的长度，约为31层- 时间复杂度：BFS搜索过程较为平稳，时间复杂度相对较低（3）A搜索算法：- 找到目标状态的搜索路径：15步- 空间复杂度：约为15层- 时间复杂度：由于A搜索算法结合了启发式信息，因此时间复杂度相对较低3. 分析：（1）DFS搜索过程可能遍历大量无效路径，导致搜索效率较低。
人工智能十五数码实验报告
目录1 实验概述22 十五数码问题分析2 2.1十五数码问题简介2 2.2可行性分析33问题的求解策略33.1算法分析33.2 A*算法设计54 实验总结64.1 实验可视化界面6 4.2个人体会74.3 详细代码：81实验概述十五数码问题来源于美国的科学魔术大师萨姆.洛伊德〔Sam I.oyd〕在1978年推出的著名的“14-15〞智力玩具。
这个游戏曾经风行欧美大陆" 。
洛伊德的创造其实只是将重排九宫〔即八数码问题〕中的3阶方阵扩大到4 阶方阵罢了。
由于这个细微的变化，十五数码问题的规模远远大于八数码问题，八数码问题的规模较小，总的状态数为9！〔=362880〕个，而十五数码问题的状态,数为16！〔〕个。
故十五数码问题更能评价一个算法的“智能〞水平。
2十五数码问题分析2.1十五数码问题简介15数码问题又叫移棋盘问题，是人工智能中的一个经典问题。
所谓的15数码问题：就是在一个4×4的16宫格棋盘上，摆放有15个将牌，每一个将牌都刻有1～15中的某一个数码。
棋盘中留有一个空格，允许其周围的某一个将牌向空格移动，这样通过移动将牌就可以不断改变将牌的布局。
这种求解的问题是：给定一种初始的将牌布局或构造(称初始状态)和一个目标布局(称目标状态)，问如何移动数码，实现从初始状态到目标状态的转变，如下列图所示。
问题的实质就是寻找一个合法的动作序列2.2可行性分析十五数码问题存在无解的情况,当遍历完所有可扩展的状态也没有搜索到目标状态就判断为无解。
可以根据状态的逆序数来先验的判断是否有解,当初始状态的逆序数和目标状态的逆序数的奇偶性一样时,问题有解；否那么问题无解。
状态的逆序数是定义如下：把四行数展开排成一行,并且丢弃数字0 不计入其中,ηi是第i 个数之前比该数小的数字的个数,那么η=Σηi 是该状态的逆序数,例如：对于初始状态：5、1、2、4、9、6、3、8、13、15、10、11、14、7、12.其η=0+0+1+2+4+4+2+6+8+9+8+9+11+6+11=81；对于目标状态：1、2、3、4、5、6、7、8、9、10、11、12、13、14、15，其η=0+1+2+3+4+5+6+7+8+9+10+11+12+13+14=105。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、15数码问题的描述及其状态空间法表示（1）15数码问题描述15数码问题又叫移棋盘问题，是人工智能中的一个经典问题。
所谓的15数码问题：就是在一个4×4的16宫格棋盘上，摆放有15个将牌，每一个将牌都刻有1～15中的某一个数码。
棋盘中留有一个空格，允许其周围的某一个将牌向空格移动，这样通过移动将牌就可以不断改变将牌的布局。
这种求解的问题是：给定一种初始的将牌布局或结构(称初始状态)和一个目标布局(称目标状态)，问如何移动数码，实现从初始状态到目标状态的转变，如图1所示。
问题的实质就是寻找一个合法的动作序列(a)初始状态(b)目标状态图1 15数码问题的一个实例（2）状态空间法表示人工智能问题的求解是以知识表示为基础的。
如何将已获得的有关知识以计算机内部代码形式加以合理地描述、存储、有效地利用便是表示应解决的问题[1]。
目前的知识表示方法有十余种，如：一阶谓词逻辑表示法、产生式表示法、状态空间表示法、语义网格表示法、框架表示法、脚本表示法、面向对象表示法等。
任何一个给定的问题可能存在多种知识表示方法，人们可以根据待求解问题的领域知识选择适当的知识表示方法。
这里我们只强调状态空间表示法。
把求解的问题表示成问题状态、操作、约束、初始状态和目标状态。
状态空间就是所有可能的状态的集合。
求解一个问题就是从初始状态出发，不断应用可应用的操作，在满足约束的条件下达到目标状态。
问题求解过程就可以看成是问题状态在状态空间的移动。
状态是为描述某类不同事物间的差别而引入的一组最少变量q0，q1，…，q n的有序集合。
问题的状态空间是一个表示该问题全部可能状态及其关系的图。
记为三元状态(S、F、G)，其中S所有可能的问题初始状态集合，F操作符集合，G目标状态集合。
十五数码的状态空间法：初始状态S[4][4]={5,12,11,4,13,6,3,10,14,2,7,9,1,15,0,8}；(0表示空格)目标状态G[4][4]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0}；操作符集合F={空格上移，空格下移，空格左移，空格右移}状态空间的一个解：是一个有限的操作算子序列，它使初始状态转化为目标状态：S0-f1->S1-f2->...f k->G。
二、A* 算法的基本原理、算法步骤、流程图（1）A*算法基本原理A*算法是一种有序搜索算法，其特点在于对评价函数的定义上。
对于一般的有序搜索，总是选择f值最小的节点作为扩展节点。
因此，f是根据需要找到一条最小代价路径的观点来估算节点的，可考虑将每个节点n的估价函数值分解为两个分量：从起始节点到节点n的最小代价路径的代价与从节点n到目标节点的最小代价路径的代价之和，也就是说f(n)是约束通过节点n的一条最小代价路径的代价的一个估计。
再定义一个函数f*，使得在任意一个节点n 上的函数值f*(n)就是从节点S到节点n的一条最佳路径的实际代价加上从节点n到目标节点的一条最佳路径的代价之和，即：f*(n) =g* (n)+h * (n)评价函数f是f*的一个估计，这个估计可由下式给出：f(n)=g(n)+h(n)其中g是g*的估计，h是h*的估计。
g* (n)的估计g(n)就是搜索树中从初始节点到当前节点n的这段路径的代价，这一代价可以由从初始节点到当前节点n寻找路径时，把遇到的各段路径的代价加起来给出。
h* (n) 的估计h(n)依赖于有关问题的领域的启发信息，于是被称作启发函数。
在启发函数中，应用的启发信息(问题知识)越多，扩展的节点就越少，这样就能更快地搜索到目标节点。
（2）A*算法基本步骤1）生成一个只包含开始节点n0的搜索图G，把n0放在一个叫OPEN的列表上。
2）生成一个列表CLOSED，它的初始值为空。
3）如果OPEN表为空，则失败退出。
4）选择OPEN上的第一个节点，把它从OPEN中移入CLPSED，称该节点为n。
5）如果n是目标节点，顺着G中，从n到n0的指针找到一条路径，获得解决方案，成功退出（该指针定义了一个搜索树，在第7步建立）。
6）扩展节点n，生成其后继结点集M，在G中，n的祖先不能在M中。
在G中安置M的成员，使他们成为n的后继。
7）从M的每一个不在G中的成员建立一个指向n的指针（例如，既不在OPEN中，也不在CLOSED中）。
把M1的这些成员加到OPEN中。
对M的每一个已在OPEN中或CLOSED中的成员m，如果到目前为止找到的到达m的最好路径通过n，就把它的指针指向n。
对已在CLOSED中的M的每一个成员，重定向它在G中的每一个后继，以使它们顺着到目前为止发现的最好路径指向它们的祖先。
8）按递增f*值，重排OPEN（相同最小f*值可根据搜索树中的最深节点来解决）。
9）返回第3步。
在第7步中，如果搜索过程发现一条路径到达一个节点的代价比现存的路径代价低，就要重定向指向该节点的指针。
已经在CLOSED中的节点子孙的重定向保存了后面的搜索结果，但是可能需要指数级的计算代价。
（3）流程图如下所示：三、实例（1）本文采用C#基于对话框的程序设计，在图形界面上显示出十五数码格局并可以随意设置数码的位置。
确定初始状态格局后，使用A*算法进行搜索。
本方法实现的程序中用到的估价函数如下：f(n)=h(n)+g(n)。
其中，h(n)代表搜索树中节点n的深度，根节点深度是0。
启发函数g(n)定义为当前节点与其目标节点相应位置不相同元素的个数。
点击初始化按钮，开始执行搜索，成功或失败后提示。
（2）程序实例展示1）0步：初始状态，输入0~16的数码输入完毕后，点击初始化，呈下图所示：2）10步：初始态如下图所示：0数码经过上移一次、左移三次、下移三次，右移三次到达目标状态，如下图：（3）性能指标空格不计，则16宫图的某状态为数1到15的一个排列，记为n0n l n2n3n4n5n6n7n8n9n10n11n12n13n14n15。
两个状态之间是否可达可以通过计算两者的逆序数来判断，若两者逆序数的奇偶性相同则可达，否则不可达。
也即对于任一个目标状态节点，有(1/2)×16 !=0个状态可达该节点。
据统计，单纯用A*算法要花费几个小时时间才能判断出不能达到目标状态，这时CLOSED表长度为0。
但由于本程序缺陷甚多，所以算法的时间复杂度会更高。
四、个人体会初学人工智能时，最先联想到的便是机器人，一直感觉机器人是非常智能且非常神秘的，这也令人工智能在我的思想里笼罩了一层非同寻常的面纱，非常迫切的想要了解它的内涵。
经过十几学时的学习，我对人工智能已有了初步了解，也深深的被它吸引，尤其通过本次程序设计，对人工智能的学习兴趣更加浓厚了！15数码问题是人工智能的一个经典的问题。
本文中通过设计一个基于A*算法的状态空间搜索程序，对于给定的初始状态，采用f(n)=h(n)+g(n)表示以当前节点与其目标节点相应位置不相同元素的个数与搜索深度之和作为启发函数的度量，并用可视化编程语言C#来实现该问题。
在程序的设计与实现过程中，遇到了很多的问题。
首先由于初学人工智能，理解上有一定的困难，对A*算法的深入学习是一个曲折的过程。
其次，在程序真正的设计及实现过程中，的确需要花费大量的精力来思考，反复试验。
所设计的程序能够运行，但缺陷还是非常之大的，如其中重排OPEN表时，没有进行真正意义上的重新排列，只是选出代价最小的放在最先的位置，这实际上对程序的运行效率有很大的影响。
同时通过输入大量的初始状态和目标状态发现，在一般情况下都可以找到最优的动作序列。
但对某些稍微复杂的初始状态虽能得到正确解却不能完全得到最短的搜索路径，对于某些极其复杂的状态，甚至得不到解。
这是有待进一步学习并改进的地方。
但本程序还是有些值得肯定之处。
界面设计比较友好，容易操作。
而且在程序开始时，就判断目标状态是否可达，这样可节约大量的时间。
虽然很多地方设计的不尽如意，但这是针对十五数码这个具体问题的一点优化。
附录：Mainext= ();if == ""){("请将所有空格填写完整！");return;}Start_Matrix[i][j] = ;}}oString();}}currentIndex = (++currentIndex) % ;if (currentIndex == 0)= false;}= i;digitalPos[matrix[i][j]].y = j;}}return digitalPos;}private int cost;public int Cost{get{return cost;}set{cost = value;}}< 3 && != 1){_15DigitalNode childNode = new _15DigitalNode, this, + 1, 2);swap(ref [digitalPos[0].x][digitalPos[0].y],ref [digitalPos[0].x + 1][digitalPos[0].y]);(objectDigitalPos);(childNode);}> 0 && != 2){_15DigitalNode childNode = new _15DigitalNode, this, + 1, 1);swap(ref [digitalPos[0].x][digitalPos[0].y],ref [digitalPos[0].x - 1][digitalPos[0].y]);(objectDigitalPos);(childNode);}< 3 && != 3){_15DigitalNode childNode = new _15DigitalNode, this, + 1, 4);swap(ref [digitalPos[0].x][digitalPos[0].y],ref [digitalPos[0].x][digitalPos[0].y + 1]);(objectDigitalPos);(childNode);}> 0 && != 4){_15DigitalNode childNode = new _15DigitalNode, this, + 1, 3);swap(ref [digitalPos[0].x][digitalPos[0].y],ref [digitalPos[0].x][digitalPos[0].y - 1]);(objectDigitalPos);(childNode);}return childNodes;}ost > ((_15DigitalNode)openList[i]).Cost)min = i;}object temp = openList[min];openList[min] = openList[0];openList[0] = temp;}evel != 0){(((_15DigitalNode)result[ - 1]).parentNode);}();return result;}}}。