考研数学线性代数常用公式

考研数学线代定理公式汇总1.行列式定理:(1) 行列式的值不变性: 对于可逆矩阵A，有det(AB) =det(A)det(B)。

(2)若存在行(列)线性相关，则行列式为0。

(3)拉普拉斯定理:对于n阶行列式，可以通过余子式展开得到。

2.线性方程组定理:(1)线性方程组存在唯一解的充要条件是系数矩阵的秩等于方程组的未知数个数，并且扩展矩阵的秩等于系数矩阵的秩。

(2)齐次线性方程组存在非零解的充要条件是系数矩阵的秩小于方程组的未知数个数。

(3)利用矩阵的逆可以求解非齐次线性方程组。

3.矩阵定理:(1)矩阵的秩等于其非零特征值的个数。

(2)若矩阵A可对角化，则A与其相似矩阵具有相同的特征值。

(3)奇异值分解定理:对于任意矩阵A，都可以分解成奇异值分解形式:A=UΣV^T，其中U和V是正交矩阵，Σ是对角矩阵。

4.向量空间定理:(1)向量组的线性相关性可以通过列向量组的秩判断，如果秩小于向量个数，则线性相关。

(2)向量组的秩等于向量组的极大线性无关组的向量个数。

(3) rank(A^T) = rank(A)，其中A是矩阵。

(4)若A和B是可逆矩阵，则(A^T)^-1=(A^-1)^T。

5.特征值与特征向量定理:(1)特征值方程的根为矩阵的特征值。

(2)若特征值λ是矩阵A的特征值，对应的特征向量组成的集合是由矩阵A-λI的零空间生成的。

(3)矩阵A相似于对角矩阵的充要条件是A有n个线性无关的特征向量。

以上是一些常见的数学线性代数定理和公式的汇总，希望对您的学习有所帮助。

当然，线性代数的内容还是比较广泛的，还有很多其他的定理和公式，如矩阵行列式的性质、特征值与特征向量的性质、矩阵的幂等性等。

如果您对这个话题有更深入的了解需求，可以提出具体的问题，我将尽力回答。

考研数学线性代数常用公式数学考研考前必背常考公式集锦。

希望对考生在暑期的复习中有所帮助。

本文内容为线性代数的常考公式汇总。

1、行列式的展开定理行列式的值等于其任何一行（或列）所有元素与其对应的代数余子式乘积之和，即A= a i1 A i1+ a i2 A i2+...+ a in A in( i =1, 2,..., n)= a1j A1j+ a 2j A2j+...+ a nj A nj( j =1, 2,..., n)推论：行列式的一行（或列）所有元素与另一行（或列）对应元素的代数余子式的乘积之和为零，即n∑a ij A kj= a i1 A k1+ a i2 A k2+...+ a in A kn=0,(i≠k )j=1n∑a ji A jk= a1i A1k+ a2i A2k+...+ a ni A nk=0(i≠k )j=12、设 A =(a ij)m⨯n，B =(b ij)n⨯k（注意 A 的列数和 B 的行数相等），定义矩阵nC =(c ij)m⨯k，其中c ij=a i1b1j+a i2b2j+...+a in b nj=∑a ik b kj，称为矩阵 A 与矩阵 B 的k =1的乘积，记作 C = AB .如果矩阵A为方阵，则定义An=A⋅A...A为矩阵 A 的 n 次幂.n个A不成立的运算法则AB≠BAAB=O≠>A =O或B=O3、设 A 为n阶方阵，A*为它的伴随矩阵则有 AA *= A * A = A E .设 A 为n阶方阵，那么当 AB = E 或 BA = E 时，有 B -1 = A4、对单位矩阵实施一次初等变换得到的矩阵称之为初等矩阵.由于初等变换有三种，初等矩阵也就有三种：第一种：交换单位矩阵的第 i 行和第 j 行得到的初等矩阵记作E ij，该矩阵也⎛ 0 0 1 ⎫ 可以看做交换单位矩阵的第 i 列和第 j 列得到的.如 E 1,3 0 1 0 ⎪= ⎪ .1 0 0 ⎪⎝ ⎭第二种：将一个非零数 k 乘到单位矩阵的第 i 行得到的初等矩阵记作 E i ( k ) ；该矩 阵 也 可 以 看 做 将 单 位 矩 阵 第 i 列 乘 以 非 零 数 k 得 到 的 . 如⎛ 1 0 0 ⎫E 2 (-5) 0 -5 0 ⎪ = ⎪ .0 0 1 ⎪⎝ ⎭第三种：将单位矩阵的第 i 行的 k 倍加到第 j 行上得到的初等矩阵记作 E ij ( k ) ；该矩阵也可以看做将单位矩阵的第 j 列的 k 倍加到第 i 列上得到的.如⎛ 1 0 0 ⎫ E 3,2 (-2) 0 1 -2 ⎪= ⎪ .0 0 1 ⎪⎝ ⎭注：1）初等矩阵都只能是单位矩阵一次初等变换之后得到的.2）对每个初等矩阵，都要从行和列的两个角度来理解它，这在上面的定义中已经说明了.尤其需要注意初等矩阵 E ij ( k ) 看做列变换是将单位矩阵第 j 列的k 倍加到第 i 列，这一点考生比较容易犯错.5、矩阵 A 最高阶非零子式的阶数称之为矩阵 A 的秩，记为 r ( A ) .1） r ( A ) = r ( A T ) = r ( k A ), k ≠ 0 ；2） A ≠ O ⇔ r (A ) ≥ 1；3） r ( A ) = 1 ⇔ A ≠ O 且 A 各行元素成比例；4）设 A 为 n 阶矩阵，则 r ( A ) = n ⇔ A ≠ 0 . 6、线性表出设 α1 , α 2 ,...,αm 是 m 个 n 维 向 量 ， k 1 , k 2 ,...k m 是 m 个 常 数 ， 则 称k 1α1 + k 2α 2 + ... + k m αm 为向量组α1 , α 2 ,...,αm 的一个线性组合.设 α1,α2 ,...,αm 是 m 个 n 维向量， β 是一个 n 维向量，如果 β 为向量组α1 , α2 ,...,αm的一个线性组合，则称向量β可以由向量组α1 , α2 ,...,αm线性表出.线性相关设α1 , α2 ,...,αm是m个n维向量，如果存在不全为零的实数k1 , k2 ,..., k m，使得k1α1+ k 2α2+...+ k mαm=0，则称向量组α1,α2,...,αm线性相关.如果向量组α1 , α2 ,...,αm不是线性相关的，则称该向量组线性无关.与线性表出与线性相关性有关的基本定理定理1：向量组α1 , α2 ,...αm线性相关当且仅当α1 , α2 ,...αm中至少有一个是其余m-1 个向量的线性组合.定理2：若向量组α1 , α2 ,...αm线性相关，则向量组α1 , α2 ,..., αm ,αm+1也线性相关.注：本定理也可以概括为“部分相关⇒整体相关”或等价地“整体无关⇒部分无关”.定理3：若向量组α1 , α2 ,...αm线性无关，则向量组α1 , α2 ,...αm的延伸组⎛α⎫ ⎛α⎫⎛α⎫也线性无关.1⎪ , 2⎪,..., m⎪⎝β1⎭ ⎝β2 ⎭⎝βm ⎭定理4：已知向量组α1 , α2 ,...αm线性无关，则向量组α1 , α2 ,...αm , β线性相关当且仅当β可以由向量组α1,α2 ,...αm线性表出.定理 5：阶梯型向量组线性无关.定理6：若向量组α1 , α2 ,...,αs可以由向量组β1 , β2 ,..., βt线性表出，且α1 , α2 ,...,αs线性无关，则有s≤t.注：本定理在理论上有很重要的意义，是讨论秩和极大线性无关组的基础.定理内容也可以等价的描述为：若向量组α1 ,α2 ,...,αs可以由向量组β1 , β2 ,..., βt线性表出，且 s > t ，则α1,α2,...,αs线性相关.对于这种描述方式，我们可以把定理内容简单地记为：“多数被少数线性表出，则必相关.”定理7：n +1个n维向量必然线性相关.7、线性方程组解的存在性设 A =(α1,α2,...,αn)，其中α1,α2,...,αn为 A 的列向量，则线性方程组 Ax = b 有解⇔向量 b 能由向量组α1,α2,...,αn线性表出；⇔r (α1,α2,...,αn)= r (α1,α2,...,αn,b )；⇔r ( A )= r ( A, b)线性方程组解的唯一性当线性方程组 Ax = b 有解时， Ax = b 的解不唯一（有无穷多解）⇔线性方程组的导出组 Ax =0有非零解；⇔向量组α1 , α2 ,...,αn线性相关；⇔r (α1,α2,...,αn)< n ；⇔r ( A )< n .注：1）注意该定理成立的前提条件是线性方程组有解；也就是说，仅告知r (A )< n 是不能得到 Ax = b 有无穷多解的，也有可能无解.2）定理 2是按照 Ax = b 有无穷多解的等价条件来总结的，请考生据此自行写出 Ax = b 有唯一解的条件.8、特征值和特征向量：设 A 为 n 阶矩阵，λ是一个数，若存在一个 n 维的非零列向量α使得关系式 Aα = λα成立.则称λ是矩阵 A 的特征值，α是属于特征值λ的特征向量.称为矩阵 A 的特征多项式.设 E 为 n 阶单位矩阵，则行列式λE - A注：1）要注意：特征向量必须是非零向量；2）等式 Aα = λα也可以写成(A - λE)α =0，因此α是齐次线性方程组( A - λE ) x =0的解，由于α ≠0，可知( A - λE ) x =0是有非零解的，故A - λE =0；反之，若 A - λE =0，那么齐次线性方程组( A - λE ) x =0有非零解，可知存在α ≠ 0 使得(A-λE)α = 0，也即Aα = λα.由上述讨论过程可知：λ是矩阵 A 的特征值的充要条件是 A - λE =0（或λE- A =0），而特征值λ的特征向量都是齐次线性方程组( A - λE ) x =0的非零 解.3）由于λE - A 是 n 次多项式，可知 A - λE =0有 n 个根（包括虚根），也即 n 阶矩阵有 n 个特征值；任一特征值都有无穷多特征向量9、矩阵的相似对角化定理1： n 阶矩阵 A 可相似对角化的充要条件是矩阵 A 存在 n 个线性无关的特征向量.同时，在等式 A = P ΛP-1中，对角矩阵Λ的元素为 A 的 n 个特征值，可逆矩阵 P 的列向量为矩阵 A 的 n 个线性无关的特征向量，并且 P 中特征向量的排列顺序与Λ中特征值的排列顺序一致.推论：设矩阵 A 有 n 个互不相同的特征值，则矩阵 A 可相似对角化.定理2： n 阶矩阵 A 可相似对角化的充要条件是对任意特征值λ，λ线性无关的特征向量个数都等于λ的重数.推论： n 阶矩阵 A 可相似对角化的充要条件是对任意特征值λ，n - r (λE - A)=λ的重数.10、设 A 为实对称矩阵（ A T= A ），则关于 A 的特征值与特征向量，我们有如下的结论：定理1： A 的所有特征值均为实数，且 A 的的所有特征向量均为实数.定理2： A 属于不同特征值的特征向量必正交.定理3：A 一定有 n 个线性无关的特征向量，即 A 可以对角化.且存在正交矩阵 Q ，使得 Q -1 AQ = Q T AQ = diag (λ1,λ2,...,λn)，其中λ1,λ2,...,λn为矩阵 A 的特征值.我们称实对称矩阵可以正交相似于对角矩阵.n n11、如果二次型∑∑a i j x i x j中，只含有平方项，所有混合项 x i x j(i ≠ j)的系i=1j =1数全为零，也即形如 d1 x12+ d 2 x22+...+ d n x n2，则称该二次型为标准形。

高等数学公式篇·平方关系：sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式：sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角函数的角度换算[编辑本段]公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－co tαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)部分高等内容[编辑本段]·高等代数中三角函数的指数表示(由泰勒级数易得)：sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数，e^z=exp(z)＝1＋z/1！＋z^2/2！＋z^3/3！＋z^4/4！＋…＋z^n/n！＋…此时三角函数定义域已推广至整个复数集。

高等数学公式篇·平方关系：sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系：sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系：tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式：sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角函数的角度换算[编辑本段]公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－co tα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)部分高等内容[编辑本段]·高等代数中三角函数的指数表示(由泰勒级数易得)：sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix)+e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数，e^z=exp(z)＝1＋z/1！＋z^2/2！＋z^3/3！＋z^4/4！＋…＋z^n/n！＋…此时三角函数定义域已推广至整个复数集。

线性代数考研公式大全线性代数考研公式大全(最新整理收集)线性代数部分基本运算①A B B A②A B C A B C③c A B cA cB c d A cA dA④cdA cd A⑤cA 0 c 0或A 0。

ATTAA B T AT BTcA Tc AT。

AB TBTATn n 1 21 C2n n 1 n2D a21A21 a22A22 a2nA2n转置值不变AT A逆值变A 11Acn, 1 2, , 1, , 2,A 1, 2, 3 ，3阶矩阵B 1, 2, 3A B A BA B 1 1, 2 2, 3 3A B 1 1, 2 2, 3 3A 0B A0BABE i,j c 1有关乘法的基本运算线性代数考研公式大全(最新整理收集) Cij ai1b1j ai2b2j ainbnj线性性质A1 A2 B A1B A2B，A B1 B2 AB1 AB2cA B c AB A cB 结合律AB C A BCAB TBTATABAkAl Ak lAklAklAB kAkBk不一定成立！AE A，EA AA kE kA，kE A kAAB E BA E与数的乘法的不同之处AB kAkBk不一定成立！无交换律因式分解障碍是交换性一个矩阵A的每个多项式可以因式分解，例如A2 2A 3E A 3E A E无消去律（矩阵和矩阵相乘）当AB 0时A 0或B 0由A 0和AB 0 B 0由A 0时AB AC B C（无左消去律）特别的设A可逆，则A有消去律。

左消去律：AB AC B C。

右消去律：BA CA B C。

如果A列满秩，则A有左消去律，即①AB 0 B 0 ②AB AC B C可逆矩阵的性质i）当A可逆时，AT也可逆，且AT1A 1T。

线性代数考研公式大全(最新整理收集)Ak也可逆，且Ak1A 1k 1数c0，cA也可逆，cA1 1A。

cii）A，B是两个n阶可逆矩阵AB也可逆，且AB 1 B 1A 1。

考研数学公式大全数学是考研的核心科目之一，而掌握必要的数学公式则是取得好成绩的关键。

以下是一份考研数学公式大全，涵盖了高等数学、线性代数和概率论与数理统计中的重要公式，希望能对备考研究生入学考试的同学有所帮助。

一、高等数学1、求导法则本文1)链式法则：f(u)f'(u)=f'(u)du本文2)乘积法则：f(u)g(u)=f'(u)g(u)+f(u)g'(u)本文3)指数法则：f(u)^n=nu'f(u)/(n-1)!2、求极值本文1)极值条件：f'(x)=0本文2)极值定理：f(x)在x=a处取得极值，则f'(a)=03、积分公式本文1)牛顿-莱布尼茨公式：∫f(x)dx=F(b)-F(a)，其中F'(x)=f(x)本文2)微分定理：d/dx∫f(x)dx=f(x)本文3)积分中值定理：若f(x)在[a,b]上连续，则至少存在一点c∈[a,b]，使得∫f(x)dx=f(c)(b-a)4、不定积分公式本文1)幂函数积分：∫x^n dx=(n+1)/n+1 x^(n+1)/n+1+C本文2)三角函数积分：∫sinx dx=cosx+C，∫cosx dx=-sinx+C 5、定积分公式本文1)矩形法：若a<=x<=b，a<=y<=b，则∫(a,b)(x^2+y^2)dx=∫(a,b)x^2 dx+∫(a,b)y^2 dx=(b-a)(x^2+y^2)/2本文2)梯形法：若a<=x<=b，a<=y<=b，则∫(a,b)(x^2+y^2)dx=∫(a,b)x^2 dx+∫(a,b)y^2 dx=(b-a)(x^2+[by]+[ax])/3二、线性代数6、行列式公式本文1)行列式展开式：D=a11A11+a12A12+...+an1An1，其中Aij为行列式中第i行第j列的代数余子式本文2)范德蒙行列式：V=(∏i=1n[(x-a)(i-1)]^(n-i)) / (∏i=1n[(x-a)(i-1)])，其中ai为行列式中第i行第i列的元素7、矩阵公式本文1)矩阵乘法：C=AB，其中Cij=∑AikBkj，k为矩阵乘法的维数本文2)逆矩阵：A^-1=(1/∣A∣)A，其中∣A∣为矩阵A的行列式值，A为矩阵A的伴随矩阵8、向量公式本文1)向量内积：〈a,b〉=a1b1+a2b2+...1、求导法则本文1)链式法则：若f是一个包含x和函数u=u(x)，则f' = f'[u(x)] * u'(x)。

数学考研必备公式总结一. 线性代数公式1. 行列式相关公式：- 二阶行列式的计算公式：$D = ad - bc$- 三阶行列式的计算公式：$D = a(ei - fh) - b(di - fg) + c(dh - eg)$ - 全排列定义的多元函数行列式：$|A| = \sum_{p \in S_n} (1 - \delta(p)) a_{1p_1}a_{2p_2} \cdots a_{np_n}$2. 矩阵运算相关公式：- 矩阵相加的运算规则：$A + B = B + A$- 矩阵相乘的运算规则：$(AB)C = A(BC)$- 矩阵的逆的性质：$(AB)^{-1} = B^{-1}A^{-1}$3. 特殊矩阵相关公式：- 对称矩阵的性质：若 $A$ 为对称矩阵，则 $A^T = A$- 正交矩阵的性质：若 $A$ 为正交矩阵，则 $A^T = A^{-1}$二. 高等数学公式1. 极限相关公式：- 函数极限的定义：$\lim_{x \to x_0}f(x) = A$ 表示对于任意给定的正数 $\varepsilon$，存在正数 $\delta$，使得当 $|x - x_0| < \delta$ 时，有 $|f(x) - A| < \varepsilon$ 成立- 常见极限公式：$\lim_{n \to \infty}(1 + \frac{1}{n})^n = e$2. 导数相关公式：- 可导函数的导数定义：$f'(x) = \lim_{h \to 0} \frac{f(x+h) -f(x)}{h}$- 常见导数公式：$(x^n)' = nx^{n-1}$3. 积分相关公式：- 不定积分的定义：$\int{f(x)dx} = F(x) + C$，其中 $F(x)$ 是$f(x)$ 的一个原函数，$C$ 是常数- 常见积分公式：$\int{x^n dx} = \frac{1}{n+1} x^{n+1} + C$三. 概率论与数理统计公式1. 随机变量相关公式：- 期望的定义：$E(X) = \sum_{x} x P(X=x)$，其中 $X$ 是一个离散型随机变量- 方差的定义：$Var(X) = E((X - E(X))^2)$，其中 $X$ 是一个随机变量2. 概率分布相关公式：- 二项分布的概率质量函数：$P(X = k) = C_n^k p^k (1-p)^{n-k}$，其中 $X$ 服从二项分布，$C_n^k$ 表示组合数3. 统计量相关公式：- 样本均值的性质：$E(\overline{X}) = \mu$，其中$\overline{X}$ 是样本均值，$\mu$ 是总体均值- 样本方差的性质：$E(S^2) = \sigma^2$，其中 $S^2$ 是样本方差，$\sigma^2$ 是总体方差结语：本文对数学考研中常用的公式进行了总结和归纳，涵盖了线性代数、高等数学以及概率论与数理统计等方面的重要公式。

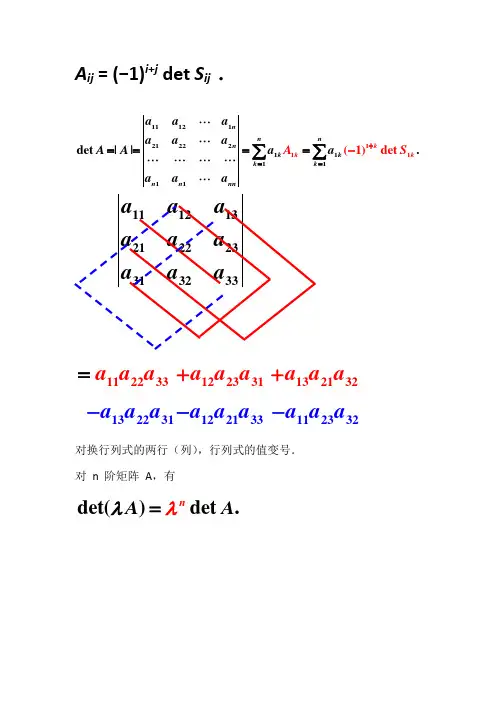
A ij = (−1)i +j det S ij ．
11
12121222111
1
1
1
111(1)de de |t t |.
n n
n
n k k k k n n nn
k k k a a a a a a A A a a S a a a A +====
==-∑∑
对换行列式的两行（列），行列式的值变号． 对 n 阶矩阵 A ，有
det()det .n
A A λλ=
11121321222331
32
33
a a a a a a a a a 132132a a a +112233a a a =122331a a a +132231a a a -122133a a a -112332
a a a -
克拉默法则
某矩阵的行列式的值不等于零，则次矩阵可逆！
N阶齐次线性方程组存在非凡解，则其行列式的值必为零；N阶齐次线性方程组的行列式的值为零，则该方程组存在非零解！
结论：梯矩阵的秩就等于非零行的行数．
B=(A,b)的含义：
如果向量集构成的矩阵的秩小于向量的个数，则该向量集线性相关！
向量集的秩等于向量集的最大线性无关子集中的向量的个数，将向量集所组成的矩阵化为梯矩阵，梯矩阵中非零行的首非零元所在的列的所有列向量组成向量集的一个最大线性无关子集！
剩余向量：
属于不同特征值的特征向量线性无关
齐次方程组有非凡解，则齐次方程组的系数行列式的值为0.
对角阵的对角线元都是它的特征值！。