数学系 研究生授课计划及课表
- 格式:doc
- 大小:146.50 KB
- 文档页数:4

数学(硕士)Mathematics(专业代码:0701)一、学科简介数学系成立于1928年,重建于1978年, 于1996年获得应用数学博士学位授予权,2002年起设立数学博士后流动站,2003年获得数学一级学科博士学位授予权。
从2004年起按数学一级学科面向全国招收和培养硕士研究生。
本学科承担了多项国家级、省部级以及横向的科研项目,曾获教育部科技进步奖一等奖、三等奖及上海市科技进步三等奖多项。
近年来。
已出版学术专著和研究生教材多本,在国内外重要核心刊物发表一批有重要影响的学术论文。
现有教授22名(其中博士生导师18名),副教授45名。
本学科毕业的硕士研究生适合到科研、生产、高新技术、信息、管理、金融、经贸等部门和高等院校从事科研、教学、科技开发和管理工作;也可以选择到数学及与数学相关的计算机信息科学、管理科学和其它高新技术学科、交叉学科攻读博士学位或进一步发展。
二、培养目标培养思想先进、品德优秀、掌握坚实的数学基础理论和系统的数学专门知识,并能够熟练应用所从事研究方向的专业技能,较为熟练地掌握一门外语,为培养从事数学研究和交叉科学研究的高级专门人才做准备。
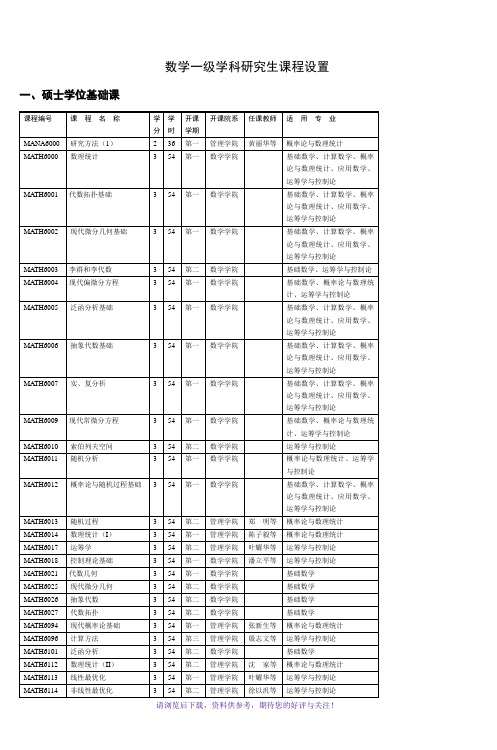
三、主要研究方向1.代数2.数论3.复分析及其应用4.偏微分方程及其应用5.数学物理6.常微分方程与动力系统7.组合数学与图论8.科学与工程计算9.概率论与数理统计10.金融数学11.运筹学与控制论四、学制和学分全日制硕士研究生学制为两年半;总学分≥43,其中学位课学分≥37。
五、课程设置说明:1.理工结合类和高校在职教师类研究生可选乙类课程,也可选甲类课程; 但高校在职教师类研究生必须选修至少一门甲类必修课(即《基础代数学》、《实复分析》与《微分流形与微分几何》,在第三学期中被列为乙类选修课),可以在第一学期或第三学期选修。
其余研究生只能选甲类课程,但可以旁听乙类课程而不计学分。
2.研究生入学前三个学期按要求选修学位课, 第四学期与第五学期可根据导师的建议按要求选修非学位课与“学术报告会”。

考研数学课程计划(数一)(总3页) --本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--全国硕士研究生入学考试数学(一)课程计划总学时:34各学科课时计划:高等数学:18学时;线性代数:8学时;概率论与数理统计:8学时《高等数学》一、函数、极限、连续(2学时)1.函数的函数极限的定义及其性质,函数的左极限和右极限;无穷小量和无穷大量的概念及其关系;无穷小量的性质及无穷小量的比较;极限的四则运算及极限存在的两个准则:单调有界准则和夹逼准则两个重要极限;函数连续的概念、函数间断点的类型初等函数的连续性闭区间上连续函数的性质;2.函数极限与连续真题讲解。
二、一元函数微分学(2学时)1.导数和微分的概念;导数的几何意义和物理意义,平面曲线的切线和法线;导数和微分的四则运算,基本初等函数的导数,复合函数、反函数、隐函数以及参数方程所确定的函数的导数;微分中值定理洛必达(L'Hospital)法则;函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘,函数的最大值与最小值;弧微分曲率的概念曲率圆与曲率半径;2.函数导数与导数应用真题讲解。
三、一元函数积分学(4学时)1.不定积分和定积分的概念;不定积分和定积分的基本性质与定积分中值定理;积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式;不定积分和定积分的换元积分法与分部积分法、有理函数、三角函数的有理式和简单无理函数的积分;反常(广义)积分与定积分的应用;2.不定积分与定积分真题讲解。
四、多元函数微分学(2学时)1.多元函数的概念;二元函数的极限与连续;多元复合函数、隐函数的求导法;二阶偏导数方向导数、梯度空间曲线的切线、法平面曲面的切平面和法线;多元函数的极值和条件极值多元函数的最大值、最小值及其简单应用;2.多元函数微分学真题讲解。
五、多元函数积分学(4学时)1.二重积分与三重积分的概念、性质、计算和应用;两类曲线积分的概念、性质及计算;两类曲线积分的关系格林(Green)公式平面曲线积分与路径无关的条件;二元函数全微分的原函数、两类曲面积分的概念、性质及计算;两类曲面积分的关系高斯(Gauss)公式、斯托克斯(Stokes)公式、计算曲线积分和曲面积分的应用;2. 二重积分、三重积分、曲线积分和曲面积分真题讲解。

研究生数学学习计划引言数学作为一门基础学科对于研究生来说是非常重要的。
数学的专业知识和方法不仅对于研究生学习其他学科,特别是理工科学科有着极大的辅助作用,而且在对于培养学生的逻辑思维和分析能力方面也起着至关重要的作用。
本文主要探讨在研究生阶段如何合理规划数学学习计划,提高数学学习成绩并且培养学生的数学能力。
一、研究生数学课程设置在研究生阶段,数学课程一般包括数学分析、高等代数、概率论与数理统计、复变函数等。
这些课程是数学基础知识的延伸和深化,对于培养学生解决问题的能力和动手能力非常关键。
因此,在学习这些课程的时候,学生需要注重理论与实际应用的结合,注重基础知识和方法的学习,注重强化数学思维和解题技巧的培养。
1.数学分析数学分析作为研究生数学的基础课程,主要内容包括实数理论、函数极限与连续、数项级数和函数项级数、微分学、积分学、函数的级数展开等。
学生在学习数学分析课程的时候,需要注重理论知识的学习和应用技巧的培养。
特别是微分学和积分学部分的内容,学生需要掌握微分与积分的基本概念和方法,能够有效地解决各类微积分问题。
2.高等代数高等代数作为研究生数学的重要课程,主要内容包括线性代数、群论、环论、域论等。
学生在学习高等代数课程的时候,需要注重抽象代数的基本概念和思想,能够灵活运用代数结构理论解决各类代数问题。
3.概率论与数理统计概率论与数理统计作为研究生数学的应用课程,主要内容包括概率空间、随机变量和概率分布、大数定律和中心极限定理、参数估计和假设检验等。
学生在学习概率论与数理统计课程的时候,需要注重概率统计理论的学习和应用技巧的培养,能够有效地解决各类概率统计问题。
4.复变函数复变函数作为研究生数学的拓展课程,主要内容包括复数域、复变函数的解析性和亚纯性、留数定理和变换、级数与积分式等。
学生在学习复变函数课程的时候,需要注重复变函数理论的学习和应用技巧的培养,能够有效地解决各类复变函数问题。
二、研究生数学学习方法在研究生阶段,数学学习方法至关重要。


学科教学(数学)专业硕士研究生培养方案(专业代码:045104)一、培养目标培养掌握现代教育理论、具有较强的教育教学实践和研究能力的高素质的中小学教师。
具体要求为:(一)拥护中国共产党领导,热爱教育事业,具有良好的道德品质,遵纪守法,积极进取,勇于创新。
(二)具有良好的学识修养和扎实的专业基础,了解学科前沿和发展趋势。
(三)具有较强的教育实践能力,能胜任相关的教育教学工作,在现代教育理论指导下运用所学理论和方法,熟练使用现代教育技术,解决教育教学中的实际问题;能理论结合实践,发挥自身优势,开展创造性的教育教学工作。
(四)熟悉基础教育课程改革,掌握基础教育课程改革的新理念、新内容和新方法。
(五)能运用一种外国语阅读本专业的外文文献资料。
二、招生对象具有国民教育序列大学本科学历(或本科同等学力)人员。
三、学习方式及年限采用全日制学习方式,学习年限一般为2年。
四、课程设置课程设置要体现理论与实践相结合的原则,分为学位基础课程,专业必修课程,专业选修课程,实践教学四个模块。
总学分不少于36学分。
学科教学(数学)全日制教育硕士专业学位研究生培养方案课程设置表关于实践教学(6学分)实践教学时间原则上不少于1年。
实践教学包括教育实习、教育见习、微格教学、教育调查、课例分析、班级与课堂管理实务等实践形式,其中第二学期最后3周在校内进行教师岗位培训,使研究生具备良好的师德和敬业精神、能够写好教案、能够辅导和答疑中小学生、具有良好的演讲能力和课堂组织能力,为履行教师职责打下坚实的基础。
第三学期到中小学进行顶岗实习。
五、教学方式要重视理论与实践相结合,采用课堂参与、小组研讨、案例教学、合作学习、模拟教学等方式。
应在中小学建立稳定的教育实践基地,做好教育实践活动的组织与实施。
成立导师组负责研究生的指导,并在中小学聘任有经验的高级教师担任指导教师,实行双导师制。
六、学位论文及学位授予(一)学位论文选题应紧密联系基础教育实践,来源于中小学教育教学中的实际问题。
研究生数学专业学习计划一、前言数学是一门深刻、纯粹、严谨的学科,是自然科学和工程技术实践中不可或缺的基础学科。
掌握数学知识和方法对于提高科学文化素质、解决实际问题、开展科学研究具有重要的意义。
作为一名数学研究生,我对数学学习具有浓厚的兴趣和学习动力。
在此,我将制定本人在研究生阶段的数学学习计划,以便更加有效的提升自己的数学水平。
二、学习目标1. 系统深入地学习数学基础理论和方法,提高数学素养;2. 掌握数学建模和解决实际问题的能力;3. 提高数学分析和推理能力,培养自己的数学思维能力;4. 积极参与数学研究,发表高水平的学术论文;5. 参加数学竞赛,提高自身数学解题能力;6. 形成较为完善的数学知识结构,为将来的数学研究和教学积累扎实的理论基础。
三、学习内容1. 数学分析、代数、几何等基础课程的学习;2. 数学建模、数学实验等课程的学习;3. 数学研究方法、数学论文写作、数学研究生实践等课程的学习。
四、学习计划1. 第一学年(1)数学分析:系统学习数学分析的基本理论和方法,掌握数学分析的常见技巧和解题方法。
(2)高等代数:学习高等代数的基本概念和基本理论,掌握高等代数的基本技巧和解题方法。
(3)数学建模:掌握数学建模的基本原理和方法,熟练掌握常见的数学建模问题的解决方法。
2. 第二学年(1)实变函数论:学习实变函数论的基本理论和方法,掌握实变函数论常见技巧和解题方法。
(2)复变函数论:学习复变函数论的基本理论和方法,掌握复变函数论的基本技巧和解题方法。
(3)数学统计:学习数学统计的基本理论和方法,掌握数学统计的基本原理和解题方法。
3. 第三学年(1)数学实验:进行一定范围的数学实验,探索不同数学问题的解决方法和实验结果。
(2)数学研究方法:学习数学研究方法和论文写作的基本技巧,提升自己的科研和论文写作能力。
(3)数学研究生实践:积极参与数学研究生实践活动,提升自己的科研水平。
五、学习方法和策略1. 培养良好的学习习惯,每天保持一定时间的数学学习;2. 注重课外阅读和实践,积极参与数学实验和实践活动;3. 培养自己的数学论文写作能力,多参加数学研究和论文撰写训练。
北大金融数学课程表研究生北大金融数学课程表(研究生)研究生阶段是北大金融数学专业学生深入学习和研究金融数学领域的重要阶段,课程设置旨在帮助学生掌握金融数学的核心理论和实践应用能力。
以下是北大金融数学研究生的课程表:第一学期:1. 高级数学分析:这门课程是研究生阶段的基础课程,通过学习数学分析的高级理论和方法,为学生打下坚实的数学基础。
2. 随机过程与金融:该课程介绍了金融领域中常用的随机过程模型和金融衍生品定价方法,帮助学生理解金融市场的随机性和不确定性。
3. 金融计量经济学:这门课程结合计量经济学和金融学的理论和方法,探讨金融市场中的经济现象和规律,培养学生的数据分析和模型建立能力。
4. 金融市场与工程:该课程介绍了金融市场的结构和运行机制,并讨论了金融工程中常用的金融产品设计和风险管理方法。
第二学期:1. 金融数学建模:该课程通过实际案例分析,培养学生的金融问题建模和求解能力,提高学生在实际金融项目中的应用能力。
2. 数值计算方法:这门课程介绍了金融数学领域中常用的数值计算方法,如数值积分、差分方程和蒙特卡洛模拟等,帮助学生解决金融问题中的数值计算难题。
3. 金融统计学:该课程探讨了金融数据的统计特性和分布规律,介绍了常用的统计方法和模型,帮助学生分析金融数据和检验金融假设。
4. 金融工程实践:这门课程通过实际项目案例,引导学生运用金融数学理论和工具解决实际金融工程问题,提高学生的实践能力和团队合作能力。
第三学期:1. 金融风险管理:该课程介绍了金融市场中的各种风险类型和风险管理方法,包括价值风险、信用风险和操作风险等,培养学生的风险识别和控制能力。
2. 金融时间序列分析:这门课程介绍了金融时间序列数据的特点和分析方法,包括ARIMA模型、ARCH/GARCH模型等,帮助学生预测金融市场的未来走势。
3. 金融市场微观结构:该课程探讨了金融市场的微观结构和交易机制,包括市场深度、委托策略和高频交易等,帮助学生理解金融市场的运行机制和交易规则。