自然对流换热计算

管道 安全端
堆焊层
管嘴
封头
图 3 堆芯补水箱进口接管接管示意图及有限元模型
4.1 强迫对流
强迫对流换热系数按照迪图斯-贝尔特（Dittus-Boelter）实验关联式[1]进行计算， k p （4） h = 0.023 ⋅ ⋅ Re 0.8 ⋅ Pr 0.3 f ID 4⋅ ρ ⋅Q p 其中：ID 为内径； Re = 为雷诺数，表征惯性力和粘性力之比的一种量度； Q 为体积 π ⋅ µ p ⋅ ID 流量。 通过计算，得到不同硼水温度下接管内壁的强迫对流换热系数，如表 1 所示。由于强迫对流
2 自然对流
根据传热学相关理论，原则上自然对流换热准则方程式应为：
2
Nu = f (Gr , Pr )
（1）

其中： Nu =
hn ⋅ L g ⋅ α ⋅ L ⋅ ∆T 为努塞尔数，表征壁面上流体的无量纲温度梯度； Gr = 为格拉晓 kp ν2
cp ⋅ µ p kp
夫数，表征浮升力和粘滞力的比值； Pr =
The Computational Method for Heat Transfer Film Coefficient of Nature Convection
Chen M eng Huang Q ing Weng Yu Jiang X ing Shen R ui
(Shanghai Nuclear Engineering Research & Design Institute, Shanghai, 200233) Abstract This paper presents a method for computing the heat transfer film coefficient of nature convection. The equation obtained from a mass of tests is used as well as ANSYS code, and an iteration is performanced by using APDL language. An example is given to indicate that the computed film coefficients are reasonable by comparing with experimental data. This method can be used in stress analysis of equipments. Key words Film Coefficient of Nature Convection, iteration, ADPL

t t t w t
u0——任意选择的参考速度
U U gtl 1 2U U V 2 X Y u0 Re Y 2 hx x U V Nu x ( ) w, x 0 Y X Y
1 2 U V X Y Re0 Pr Y 2
u u 2u u v g (t t ) 2 y y x
பைடு நூலகம்
u u 2u u v g (t t ) 2 y y x
无量纲温度：
其他无量纲：
x y u v X ;Y ; U ; V l l u0 u0
2 gtl Gr 2 u0l 2 u 02 Re 0 ( ) gtl 3 Gr 格拉晓夫数(Grashof number) 2 Gr：浮升力与粘性力的相对大小。Gr越大，浮升力的相对作 用越大，自然对流越强 U U Gr 1 2U U V 2 X Y Re Re Y 2
6.3 自然对流
Natural Convection Heat Transfer
一、概述
静止的流体，与不同温度的 固体壁面相接触，热边界层 内、外的密度差形成浮升力 （或沉降力）
f B ( f ) g gt
导致流动
固体壁面与流体的温差是 自然对流的根本原因
层流：GrPr<108 湍流：GrPr>1010 过渡区： 108<GrPr<1010 自模化现象： 在常壁温或常热流边 界条件下，达到旺盛 紊流时，hx将保持不 变，与壁面高度无关
3 2 Pr Nu x 4 5(1 2 Pr1/ 2 2 Pr) hx x
1/ 4
(Grx Pr)1/ 4

自然对流换热系数公式
自然对流是一种重要的热传递方式，广泛应用于工程领域中。

在自然对流过程中，流体的热量通过差异温度驱动而传递，换热系数是描述这种传热方式的关键参数之一。

自然对流换热系数公式可表示为：
h = (k / L) * (Gr * Pr)^n
其中，h表示换热系数，k表示流体的热导率，L表示特征长度，Gr表示重力数，Pr表示普朗特数，n表示经验系数。

在该公式中，重力数和普朗特数是自然对流换热中的两个重要无量纲参数，Gr数代表了重力的作用，Pr数则代表了流体的性质。

经验系数n的大小取决于具体的流体和几何形状等因素。

需要注意的是，自然对流换热系数公式是基于实验数据和经验公式推导而来的。

因此，在具体应用中，需要根据实际情况进行修正和校准，以获得更精确的结果。

- 1 -。

对流传热系数的计算公式
对流传热系数是热传导中的一种传热方式，常用于热交换器、冷却塔、加热器等传热设备的设计与计算中。

对于流体在壁面上的流动，其对流传热系数与流速、温度、粘度等变量密切相关。

在实际应用中，针对不同的流体与流动状态，可采用不同的计算公式。

下面列举几种常用的对流传热系数计算公式：
1. 自然对流传热系数公式：
h = 1.13 * (gβΔT)^1/4
其中，h为对流传热系数，g为重力加速度，β为热膨胀系数，ΔT为壁面温度与流体温度的差值。

2. 强制对流传热系数公式：
Nu = CRe^mPr^n
其中，Nu为努塞尔数，Re为雷诺数，Pr为普朗特数，C、m、n 为经验系数。

3. 线性对流传热系数公式：
h = kΔT
其中，k为比例常数，ΔT为温度差值。

需要注意的是，以上公式仅适用于理想条件下的流动状态，而实际应用中因存在多种不确定因素，其计算结果仅供参考，具体设计与计算仍需进行实际测试与验证。

- 1 -。

然对流换热。

工程中常见这种流动，如：

炉壁的散热；
热力管道的散热；
钢包和铸模内的钢液与壁面间的传热等。
3
2 自然对流换热边界层

热的竖壁如图：在壁的下部，自然对流刚开始形成，流动是有规则的层 流，在壁的上部，流动转变为紊流。
B处条纹已部分紊乱，说明流 动开始向湍流转变。
A处的条纹整齐 ，为层流。
使用范围： 直管；
Re ＞104; Pr ＝ 0.7～120
L/d ＞50
温差限制： 气体： △t ≤50℃ 水： △t ≤30℃ 油类： △t ≤10℃
温差不同时管内流速的畸变
20
5 管内湍流时的对流换热
关于修正：
•
• •
大温差的修正
入口段修正 （当 L/d ＜60 时） 弯曲管道的修正
•
层流时的计算
解 解 170 10 170 10 170 10 定性温度为 T 90 ℃ 定性温度为 T 90 ℃ m m 定性温度为 T 90 ℃ m 2 2 2 查表得 0 0313 W /( m ℃ 0 .. 0313 W /( m ℃ )) m 查表得 m 0 . 0313 W /( m ℃ ) m 66 22 ＝ 22 . 10 10 m 6m ＝ 22 . 10 10 m m ＝22.10 10 m 2/ / /ss s
以此计算处的 h为壁面平均 换热系数。

特征尺寸取板长；Re中的速度取主流速度。
13
2 外掠平板

例题：24℃的空气以60m/s的速度外掠一块平板，平壁保持216 ℃的温
度，板长0.4m。试求平均换热系数。（不计辐射换热） ( T ( 24 ) (T T TT )) ( T w ff ) (216 216 24 )) ( T T ( 216 24 ww ( 216 24 ) f ( T T ) w f ) ( 216 24 ) w f 解 定性温度 T 120 ℃ 解 定性温度 T 120 ℃ 解 定性温度 T 120 ℃ 解 120 ℃ m m 解 定性温度 定性温度 Tm T 120 ℃ mm 2 2 22 2 2 2 2 2 2 6 2 6 2 6 6 （m 2 2 2 查表得 25 . 10 查表得 ＝ ＝ 25 45 10 m /s s ） 查表得 ＝ 25 ..45 10 （ m / s 查表得 ＝ 25 ..45 45 10 （ m / s ） 查表得 ＝ 25 45 10 6（ （ m/ /） s） ） 2 2 2 2 3 . 34 10 /( m )] 3 . 34 10 [W W /(/( m ℃ )] 3 . 34 10 [ m ℃ )] 3 . 34 10 [ W /( m ℃ ℃ )] 3.34 10 2 [ [W W /( m ℃ )] Pr 0 686 Pr 0. . 686 Pr 0 ..686 Pr 0 . 686 Pr 0 686 u 60 0 4 uu ll ff l 60 0. . 4 u 60 0 ..4 5 60 0 . 4 u l 55 f lf 60 0 4 5 f 5 雷诺数 Re ＝ 9 . 43 10 雷诺数 Re ＝ 9 . 43 10 雷诺数 Re ＝ 9 . 43 10 雷诺数 ＝ 9 . 43 10 6 雷诺数 Re Re ＝ 9 . 43 10 6 6 6 . 10 25 45 10 25 ..45 10 25 ..45 45 10 25 25 45 10 6 5 55 5 Re 5 10 Re 5 10 Re 5 10 Re 5 10 Re 5 105 平板后部已达湍流区， 则有准数方程为 平板后部已达湍流区， 则有准数方程为 平板后部已达湍流区， 则有准数方程为 平板后部已达湍流区， 则有准数方程为 平板后部已达湍流区， 则有准数方程为

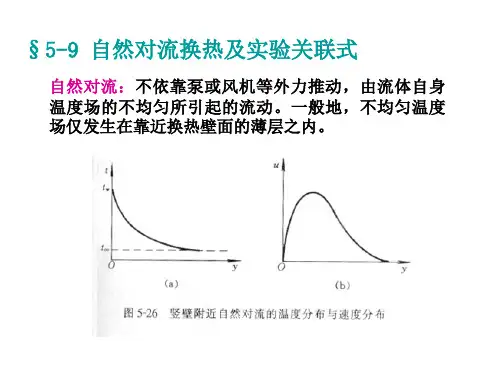
自然对流换热及实验关联式自然对流是流场温度分布不均匀导致的密度不均匀分布，在重力场的作用下产生的流体运动过程。

而自然对流换热则是流体与固体壁面之间因温度不同引起的自然对流时发生的热量交换过程。

如图 4 － 25 所示的几种自然对流的情况，前三种为大空间自然对流换热，后两种为受限空间的自然对流换热。

在自然界、在现实生活中、以及在工程上，物体的自然冷却或加热都是以自然对流换热的方式实现的。

例如，在偏僻地区，一些平时无人看管的小变电站或电话中继站等，其发热设备往往靠自然对流冷却。

此外，管道、输电线的散热、电子器件的散热、暖气片对室内空气的散热以及海洋环流、大气环流等都与自然对流有关。

由于自然对流换热的换热强度比较弱，尤其是在空气环境下，同时还存在着辐射换热，而且在温度比较高的情况下，辐射换热的强度与自然对流换热的强度处于相同的数量级。

因此，在自然对流换热的实际计算中辐射换热是不可随意忽略的。

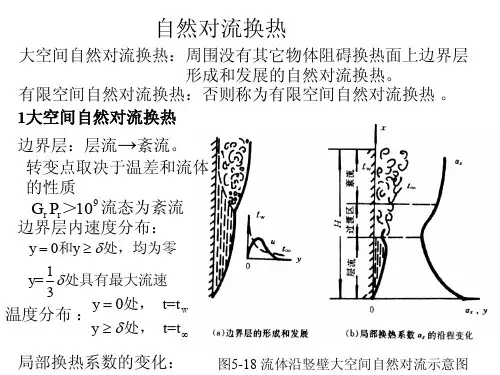
一、大空间自然对流的流动和换热特征自然对流与受迫对流最大的不同点在于流体的运动是由于温度差引起的，因而流体与换热是密不可分的。

为了讨论自然对流的流动和换热特征，这里以竖直平板在空气中的自然冷却过程为例来进行分析，如图 4 － 26 所示。

竖直平板在空气中冷却，由于空气的黏度很小，因温度差引起的流体流动的范围十分有限。

在垂直于壁面的方向上流体的速度从壁面处的 u w =0 ，逐步增大到最大值 u max ，再往后又逐步减小到 u ∞ =0 。

这种流体速度变化的区域相对于流体沿着平板上升方向（图中的 x 方向）的尺度是很薄的，因而可以称之为自然对流的速度边界层，其厚度δ (x) 仍然采用受迫对流边界层的约定方法。

它与受迫对流的速度边界层很相似，但也有显著的差别。

主要体现在速度剖面（ y 方向上的速度分布）的不同上，自然对流边界层中速度从零经最大值后在到零值，而受迫对流边界层中速度从零变化到最大值，即来流速度。

与速度边界层同时存在的还有温度发生显著变化的薄层，也就是温度从 t w 逐步变化到环境温度 t ∞热边界层，其厚度与速度边界层大致相当。

自然对流换热实验报告一、实验目的（1）了解空气沿水平圆柱体表面自然流动是的换热过程，掌握实验测试技术。

（2）测定单管（水平放置）的自然对流换热系数h 。

（3）根据实验测得的有关数据，计算各实验管的Nu 数、Gr 数和Pr 数，然后用作图法或最小二乘法确定经验方程式n Gr c Nr Pr)(=中的c 值和n 值，并给出Pr Gr 的范围。

二、实验原理对铜管进行加热，热量是以对流和辐射两种方式来散发，所以对流换热量为总流量与辐射热量之差。

即r h c Φ-Φ=Φ （W ）式中：)(f w c t t hA -=Φ；UI h =Φ；⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=Φ4f 4w 0100T 100T A c r ε，所以⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛---=4f 4w 0100T 100T )()(f w f w t t c t t A UIh ε[]）（K /W ∙m 式中：c Φ为对流换热量，W ；h Φ为加热器产生的热量，W ；r Φ为辐射换热量，W;U 加热器电压，V ；I 为加热器电流，A ；ε为圆柱体表面黑度，ε=0.064；0c 为黑体辐射系数，）（420K m /W 67.5∙=c ；w t 为管壁平均温度，℃；f t 为玻璃室内空气温度，℃；A 为圆柱体的表面积，m 2；h 为自然对流换热系数，）（K /W 2∙m 。

当实验管表面温度稳定时，测定每根管的加热电压U 、电流I 、管壁温度w t 、玻璃室内温度f t ，从表中查出圆管的直径和长度，计算出圆管表面积A ，计算出其对流换热系数h 。

根据相似理论，自然对流换热的准则为Pr),(Gr f Nr =在工业中广泛使用的是比式更为简单的经验方程式，即n Gr c Nr Pr)(=式中：c 、n 是通过实验所确定的常数（在一定的Pr Gr 数值范围内）。

为了确定上述关系式的具体形式，根据测量数据计算结果求得努塞尔准则Nu 、格拉晓夫准则Gr 和普朗特准则Pr ，即λhDNu =； 23υβtD g Gr ∆=； a υ=Pr式中：Pr 、β（空气的体胀系数，1/K ）、υ（空气的运动黏度，m 2/s ）等、λ（空气的导热系数，℃）（∙m /W ）等物性参数由定性温度）（2fw t t +从气体的热物理性质表查取；2/8.9s m g =；D 为圆管壁面定型尺寸，m ；f w t t t -=∆，℃。

自然对流换热
大空间自然对流换热：周围没有其它物体阻碍换热面上边界层 形成和发展的自然对流换热。
有限空间自然对流换热：否则称为有限空间自然对流换热 。
1大空间自然对流换热
边界层：层流→紊流。
转变点取决于温差和流体 的性质 Gr Pr＞109 流态为紊流 边界层内速度分布：
y 0和y 处，均为零
y= 1 处具有最大流速
形成厚 15 mm 的竖直空气夹层。试计算通过空气夹层的自然
对流换热量。
解 定性温度 tm (tw1 tw2 ) / 2 (100 40) / 2 70℃，据此查附录得，空气物性
1.029 kg/m3 ， 20.02106 m2/s ， 0.0296 W/(m 1m/
4
(
h
)1/
9
Gr Pr 2 105 ~ 1.1107 时，
Num
0.073(Gr
Pr
)1m/
3
(
h
)1/
9
（5-32）
（5-33） （5-34）
以上各式的适用范围为： Pr 0.5 ~ 2 h / 11 ~ 42
准则的定，性温度 : tm (tw1 tw2 ) / 2
例 5-8 温度分别为 100℃和 40℃，面积均为0.50.5 m2 的两竖壁，
)1/
9
0.197
(1.002
104
)1m/
4
(
0.015 0.5
)1/
9
1.335
Num 1.335 0.0296 2.63 W/(m2 K)
0.015
自然对流换热量为
Q Ft 2.63(0.50.5)(100 40) 39.5 W
作业
1. 4.

自然对流换热系数与面积
首先，根据牛顿冷却定律，自然对流换热系数h与表面积A之间的关系可以表示为Q = hAΔT，其中Q是通过表面的热量，ΔT是流体和表面的温度差。

从这个方程可以看出，换热系数h与表面积A成正比。

换句话说，表面积的增加会导致更多的热量传递，从而增加换热系数。

其次，自然对流换热系数与表面积之间的关系还受到表面形状和流体性质的影响。

对于相同的表面积，不同形状的表面对流体的影响也不同，因此换热系数也会有所不同。

此外，流体的性质如粘度、密度和导热系数也会影响自然对流换热系数与表面积之间的关系。

最后，需要注意的是，自然对流换热系数与表面积之间的关系并不是线性的，而是受到多种因素的综合影响。

因此，在实际工程中，需要综合考虑流体性质、表面形状和表面积等因素，通过实验或计算得出适合的换热系数值。

综上所述，自然对流换热系数与表面积之间的关系是复杂而多变的，需要综合考虑多种因素才能准确描述。

在工程设计和实际应
用中，需要根据具体情况进行分析和计算，以获得合适的换热系数值。

q
t 1 Rt
t
1
1 2

20 (20) 257.65W m 2 1 0.4 10－2 1 10 0.762 20
Q＝Fq 100 80 10－4 257. ＝20：传热系数 k 1 1
C 和 m 的值见下表。
叉排或顺排、管间距不同时，C、m的选取
Nu C Re
m
排数的影响见教材P202
表16－2
第二节
自然对流换热
流体受壁面加热或冷却而引起的自然对流换热 与流体在壁面附近的由温度差异所形成的浮升力有 关。不均匀的温度场造成了不均匀的密度场，由此 产生的浮升力成为运动的动力。在热壁面上的空气 被加热而上浮,而未被加热的较冷空气因密度较大而 下沉。所以自然对流换热时,壁面附近的流体不像受 迫对流换热那样朝同一方向流动。一般情况下，不 均匀温度场仅发生在靠近换热壁面的薄层之内。在 贴壁处，流体温度等于壁面壁面温度tW，在离开壁 面的方向上逐步降低至周围环境温度。
后排管受前排管尾流的扰动作用对平均表面传热系数的影 响直到10排以上的管子才能消失。 这种情况下，先给出不考虑排数影响的关联式，再采用管 束排数的因素作为修正系数。 气体横掠10排以上管束的实验关联式为
Nu C Rem
式中：定性温度为 tr (tw tf )/ 2; 特征长度为 管外径d， Re 数中的流速采用整个管束中最窄截面处 的流速。 实验验证范围： Ref 2000 ~ 40000。
边界层的成长和脱体决定 了外掠圆 管换热的 特征 。
可采用以下分段幂次关联式：
; 式中：C及n的值见下表；定性温度为 (tw t )/ 2 特征长度为管外径； Re 数的特征速度为来流速度 u 。

• 由于在薄层外Байду номын сангаас
u v 0
，从上式可推得
2
u u 1 dp u u v g 2 x y dx y
dp g dx
将此关系带入上式得
引入体积膨胀系数 ：
u u g 2u u v ( ) x y y 2
一般认为，
g tl 3 2 Gr 2 2 2 ul Re2
Gr / Re2 0.1 时，自然对流的影响不能忽略，
而
Gr / Re2 10 时，强制对流的影响相对于自然对流可以
忽略不计。
自然对流对总换热量的影响低于10％的作为纯强制对流； 强制对流对总换热量的影响低于10％的作为纯自然对流； 这两部分都不包括的中区域为混合对流。
按此式整理的平板散热的结果示于下表。
这里流动比较复杂，不能套用层流及湍流的分类。
二. 有限空间自然对流换热 这里仅讨论如图所示的竖的和水平的两种封闭夹层的自然 对流换热，而且推荐的冠军事仅局限于气体夹层。
封闭夹层示意图 ( tw 1
tw 2 )
夹层内流体的流动，主要取决于以夹层厚度 为特征长度的 Gr 数：
当 Gr 极低时换热依靠纯导热： 对于竖直夹层，当 Gr 2860

g t 3 Gr 2
对水平夹层，当
Gr 2430。
另：随着 Gr 的提高，会依次出现向层流特征过渡的 流动（环流）、层流特征的流动、湍流特征的流 动。 对竖夹层，纵横比
H / 对换热有一定影响。
一般关联式为
常数C和n的值见下表。
注：竖圆柱按上表与竖壁用同一个关联式只限于以下 情况： d 35
H

GrH1 / 4

多取截面平均流速。
定性温度：计算物性的定性温度多为截面
上流体的平均温度（或进出口截面平均温
度）。
1 ' " t f (t f t f ) 2
1。管内层流换热关联式
实际工程换热设备中，层流时的换热
常常处于入口段的范围。可采用下列齐德
－泰特公式：
Re f Pr f Nu f 1.86 l/d
状凝结理论
1 、凝结换热现象
蒸汽与低于饱和温度的壁面接触时，将汽化
潜热释放给固体壁面，并在壁面上形成凝结液的
过程，称凝结换热现象。有两种凝结形式。
2 、凝结换热的分类
根据凝结液与壁面浸润能力不同分两种
(1)膜状凝结
定义：凝结液体能很好地湿润壁面，并 能在壁面上均匀铺展成膜的凝结形式， 称膜状凝结。
du y 时， dy

0, t t s
求解上面方程可得： (1) 液膜厚度
4l l ( ts tw )x 2 g l r
1/ 4
ts tw 定性温度： t m 2
注意：r
按 ts 确定
(2) 局部表面传热系数
gr hx 4l ( t s t w )x
对流换热那样朝同一方向流动。
一般情况下，不均匀温度场仅发生在靠近换热壁面的薄层 之内。在贴壁处，流体温度等于壁面壁面温度tW，在离开壁面
的方向上逐步降低至周围环境温度。
定义： 由流体自身温度场的不均匀所引起的流动称为自然对流。 工程应用： 暖汽管道的散热 不用风扇强制冷却的电器元件的散热 事故条件下核反应堆的散热 产生原因： 不均匀温度场造成了不均匀密度场，浮升力成为运 动的动力。

对流换热系数的确定核心提示：1.自然对流时的对流换热系数炉墙、炉顶和架空炉底与车间空气间的对流换热均属自然对流换热。

2.强制对流时的对流换热系数(1)气流沿1.自然对流时的对流换热系数炉墙、炉顶和架空炉底与车间空气间的对流换热均属自然对流换热。

2.强制对流时的对流换热系数(1)气流沿平面强制流动时气流沿平面流动时，烧结炉其对流换热系数可按表1-1的近似公式计算。

表1-1对流换热系数计算vo=C4.65(m/s) x；o>4.65(m/s)光滑表面a=5.58+4.25z'o a^V.Slvg78轧制表面a-=5.81+4.25vo a=7.53vin.粗糙表面o=6.16+4.49vo a=T.94vi78气流沿长形工件强制流动时当加热长形工件时，循环空气对工件表面的对流换热系数可用下述近似公式计算气流在通道内层流流动时气流呈层流流动时，对流换热系数主要决定于炉气的热导率，而与炉气的流速无关。

绝对黑体的概念当物体受热后一部分热能转变为辐射能并以电磁波的形式向外放射，其波长从lfmi到若干m。

各种不同波长的射线具有不同性质，可见光和红外线能被物体吸收转化为热能，称它们为热射线。

各种物体由于原子结构和表面状态的不同，其辐射和吸收热射线的能力有明显差别。

当能量为Q的一束热射线投射到物体表面时，也和可见光一样，一部分能量Qa将被吸收，一部分能量Qr被反射，还有一部分能量Qu透射过物体(如图1-5)。

按能量守恒定律则有图1-5辐射能的吸收、反射和透过如果A=l，则R=D=0，即辐射能全部被吸收，这种物体称绝对黑体，简称黑体。

如果R=l，则A=D=0，即辐射能全部被反射，这种物体称绝对白体，简称白体。

如果D= 1，则A=K=0，即辐射能全部被透过，这种物体称绝对透过体，简称透过体。

自然界中，黑体、白体和透过体是不存在的，它们都是假定的理想物体。

对于一种实际物体来说数值，不仅取决于物体的特性，还与表面状态、温度以及投射射线的波长等有关。

对流换热量计算公式对流换热是物体或空气内气体粒子之间相互间接接触而发生的热量交换过程。

它包括散射传播，比如温度差引起的热量传递，以及气体内的温度梯度能引起的热量传导现象。

由于温度梯度的影响，高温气体中的分子热和体积能释放出来，从而使得低温气体中的分子热和体积能增加，从而使低温气体向周围空气温度高的方向辐射热量，从而实现换热。

二、对流换热量计算公式对流换热量计算公式可以用来衡量对流换热的大小：Q=hA(T2-T1)，其中，Q是换热量，单位是W，h是换热系数，A是换热表面积，单位是m2，T1、T2分别为表面温度向量的温度值。

当换热的表面积A和温度差都是已知的时候，可以使用以上计算公式来计算换热量Q。

此时换热系数h通常被称为对流换热系数，对流换热系数又可以分为气体对流换热系数、液体对流换热系数和固体对流换热系数。

气体对流换热系数是指空气中气体的换热系数，用来衡量气体的换热能力。

由于气体的存在，空气中总有一个温度分布，温度越高的区域总是以一定的速率向温度越低的区域辐射热量，而这个热量辐射机制就是指气体对流换热的作用，也就是气体对流换热系数。

液体对流换热系数指的是液体中液体粒子间温度差引起的换热现象。

由于液体比空气有更大的密度，所以液体换热速度也比空气更快，因此液体对流换热系数也比气体对流换热系数要大。

固体对流换热系数指的是固体中固体粒子间温度差引起的换热现象。

由于固体的热传导性能比液体好，因此固体对流换热系数也比液体对流换热系数要大。

三、计算步骤1.首先，要计算对流换热量，就必须知道不同表面之间的温度差，以及换热表面积A，换热系数h；2.其次，建立热力学平衡模型，利用模型来计算换热量Q；3.最后，根据换热量和换热表面积来求得温度差。

四、注意事项1.在求解对流换热量时，一定要正确地估算换热表面积和对流换热系数，以精确地求出换热量；2.表面的表面粗糙或表面的湿度会影响对流换热，因此在计算过程中应考虑清楚；3.在计算过程中，也要考虑温度梯度本身也会随着温度而变化，温度梯度越大，温度差就越大，换热量也会越大。

③弯管：
d 气体：c R 1 1.77 R
d 液体： c R 1 10 .3 R
3
④非圆管：当量径：de = 4Ac/P 2.外部流： 2.1 平板：
1/3 2.1.1 层流： Nu x 0.332 Re 1x/ 2 Pr x /5 1/3 2.1.2 湍流： Nu x 0.0296 Re 4 Pr x x
1．无限空间:
Nu cGr Pr ,
n
Gr Pr 区分层流、湍流，c,n 取值见 P161，表 3.7 2．有限空间： n H Nu cGrd Pr ( ) m 1/ 4 H 空气，竖立： Nu 0.197Grd Pr ( ) 1 / 9 (8.6×103<Grd<2.9×105）
2.2 管外流 2.2.1 单管：
1/3 Nu c Re n Prx
c,n 取值：圆管见表 3.3，非圆管见表 3.4, P158
0.62 Re1 / 2 Pr 1 / 3 Re 5 / 8 4 / 5 或：邱吉尔-朋斯登公式： Nu 0.3 [1 ( ) ] 2 / 3 1/ 4 282000 [1 (0.4 / Pr) ]
空气，水平： Nu 0.212Grd Pr
Nu 0.061Grd Pr
1/ 4
(1×104<Grd<4.6×105） (Grd>4.6×105）
1/ 3
5 8 /5 1/3 前层流后湍流： Nu x (0.0037 Re 4 x 871) Pr x （0.6<Pr<60,5×10 <Re<10 ）
/2 1/3 ，பைடு நூலகம்0.664 Re1 x Pr x
（0.6<Pr<60）

对流换热公式一、强制对流换热粘性流体强制流：⎪⎪⎭⎝⎫ ⎛=Pr Re,,l f Nu 0l 或 ⎪⎪⎭⎫ ⎝l 01．内部流（管内流，（长管l/d>60,短管l/d<60））⎛=Pe lf Nu Re,, 1.1湍流①迪特斯-波尔特Dittus-Boelter 公式：__,条件：__气体≤50℃，水≤20~40℃，油类≤10℃。

Re=104-1.2×105_， 定性温度为：流体平均温度，定性尺寸为：管内径。

n Nu Pr Re 023.08.0=②温差大：修正或1.2层流列齐德-泰特公式：__14.031Pr Re 86.1⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=w f l d Nu μμ________ 1.3过渡流：格尼林斯基公式： ⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦f (f 8)(Re -1000)Pr d Nu=1+c l t修正：①温差（加热或冷却）：⎪⎪⎭⎫ ⎝⎛w fPrPr 或⎪⎪⎭⎫ ⎝⎛w f μμ 或⎪⎪⎭⎫⎝⎛w f T T ②入口段（短管l/d<60）：kd l ⎪⎭⎫ ⎝⎛或 7.01⎪⎭⎫⎝⎛+=l d c l③弯管： R d c R 77.11+=气体： 33.101⎪⎭⎫ ⎝⎛+=R d c R 液体： ④非圆管：当量径：de = 4Ac/P2.外部流： 2.1平板：2.1.1 层流： ， （0.6<Pr<60） 1/32/1Pr Re 332.0x x x Nu =1/32/1Pr Re 664.0x x 2.1.2湍流： 1/35/4Pr Re 0296.0x xx Nu =前层流后湍流：（0.6<Pr<60,5×105<Re<108） 1/35/4Pr )871Re 0037.0(xx x Nu -=恒热流：1/35/4Pr Re 0308.0x x x Nu =2.2管外流 2.2.1单管：1/3n Pr Re xc Nu = c,n 取值：圆管见表3.3，非圆管见表3.4, P158 或：邱吉尔-朋斯登公式：5/48/54/13/2])282000Re (1[]Pr)/4.0(1[Pr Re 62.03.0+++=Nu 3/12/1温度：流体与管壁的平均温度, 长度：管外径2.2 管簇25.021)Pr Pr ()(Pr Re w f p m n s s c Nu = S1,S2为间距，各常数见表3.5, P159管排修正系数εz， εz 的值见表3.6，P160二、自然对流换热:粘性流体自由流动：⎪⎪⎭⎫ ⎝⎛=Pr ,,0Fr llf Nu 或 ⎪⎪⎭⎫ ⎝⎛=Pr ,0Gr llf Nu 1．无限空间:()nGr ,Pr Gr 区分层流、湍流，c,n 取值见P161，表3.7c Nu Pr =2．有限空间：()m n Hd Gr c Nu )(Pr δ=空气，竖立：()9/1)(Pr 197.0=4/1-δH4/13/1Gr Nu d (8.6×103<Gr d <2.9×105）空气，水平： (1×104<Gr d <4.6×105） ()Pr 212.0d Gr Nu =()Pr 061.0d Gr Nu = (Gr d >4.6×105）。

自然对流换热系数对流传热系数一般指表面传热系数。

对流传热基本计算式——牛顿冷却公式中的比例系数，以前又称为对流换热系数，是由流体内部各部分质点发生宏观运动而引起的热量传递过程，只能发生在有流体流动的场合单位是w/(㎡*k)，含义是对流换热速率，反应了对流传热的快慢，对流传热系数越大，表示对流传热越快。

原理表面传热系数通常靠实验方法确认。

流体的热传导促进作用对于对流成套过程存有非常大影响。

流体流动时与壁面出现摩擦，摩擦力并使流体运动中断，越紧邻壁面的流体流动速度减少越多，紧扣壁面的流体几乎停滞不前。

在摩擦的迟滞促进作用明显影响范围内，壁面附近构成一层很厚的流动边界层。

流体流动速度越大，流体对壁面的冲刷促进作用越弱，流动边界层越厚，薄薄的流动边界层之所以令人高度关注是因为构成与它有关的成套边界层(也表示温度边界层)。

不论是壁冷却流体还是流体冷却壁，热流都必须通过成套边界层展开热传导传达。

在返回成套边界层步入主流区之后，流体对流混合促进作用进一步增强。

边界层的热传导热阻形成对流成套热阻的主要部分，成套温差的大部分促进作用在薄薄的边界层。

表面传热系数是对流传热基本计算式——牛顿冷却公式（newton‘s law of cooling）中的比例系数，一般记做h，以前又常称对流换热系数，单位是w/(㎡*k)，含义是对流换热速率，在数值上等于单位温度差下单位传热面积的对流传热速率。

公式表面传热系数符号为h，(α)；q =h(ts-tr)。

式中：ts是表面温度；tr是表征外部环境特性的参考温度。

热学的量。

si单位：w/(m2·k) (瓦〔特〕每平方米开〔尔文〕)。

牛顿加热公式：流体被冷却时 q=h（tw-tf）流体被冷却时 q=h（tf-tw）其中，tw及tf分别为壁面温度和流体温度，℃。

如果把温差（亦称温压）记为δt，并签订合同永远为正值，则牛顿加热公式可以则表示为：q=hδtφ=haδt其中q为热流密度，单位就是瓦/平米（w/㎡），φ为热流，单位就是瓦（w）。