多次级高压变压器的分布电容

开发研究高频变压器设计时的漏电感和分布电容的探究广东省东莞市大忠电子有限公司曹洪武摘要：电源、家电、通讯等使用的高频变压器,通常需要控制漏电感、分布电容等电性参数。

设计时，为了降低成本，选择常规材料是首选;为了有竞争力也会选用常规结构，这样可以省工时。

但随着技术的提升，终端产品要求的提高,对相应的零部件等的要求也提高了，因此元器件也随着终端产品的要求而提高。

高频变压器的技术也在提高，变压器的参数达到更好地配合终端产品，除了材料方便的选择，还有结构方面也可以调整,配合达到终端产品的要求。

本文对高频变压器设计时的漏电感和分布电容展开了研究,具有一定的参考借鉴价值。

关键词:变压器;漏电感;分布电容0 引言设计变压器时候，需要综合考虑材料、性能、结构和成本等要素，以充分满足其性能。

但变压器的漏电感与分布电容不容易同时满足,一般情况漏电感减小，那么分布电容就会上升，而分布电容减小,那么漏电感就会上升。

因此，在设计变压器时，针对不同的变压器，选择不同的材料,也要选择不同的结构，这样选择才能更好达到性能要求，更适合终端使用。

(1) 漏电感是变压器中一次绕线与二次绕线的耦合系 数。

数值较小时，构成变压器的绕线的一部分不会有变压作用，而是与Choke Coil有等效成分所产生的。

若一次绕线与二次绕线完全耦合（耦合系数k=l)为理想的变压器时，漏电感数值为零。

但一般变压器的耦合系数多为1以下，因为未完全耦合，所以绕线的一部分才会有电感的功能。

(2)分布电容是指由非电容形态形成的一种分布参数。

带电电缆、变压器对地都有一定的分布电容，而分布电容大小取决于电缆的几何尺寸、电缆的长度和绝缘材料等，它由2个存在压差而又相互绝缘的导体所构成。

1变压器中有漏电感和分布电容一般在变压器中存在不少于2个绕组，由定义可以看出变压器中存在着2个参数，就是漏电感和分布电容。

变压器初级与次级至少各1个绕组,有的变压器初级与次级超过2个绕组以上，因此变压器中就存在了漏电感和分布电容。

高频变压器分布电容研究综述变压器寄生参数、分布参数在高频下对变压器的影响成为制约高频、高磁导率、小体积变压器研究的重要因素，也是该领域研究的重点。

本文对近几年高频变压器分布电容的研究情况进行了总结，首先重点介绍了现有的高频变压器模型，并分析了高频变压器分布电容对电路的影响，最后总结了抑制分布电容的方法。

同时文章指出该领域今后的研究方向：磁导率与寄生参数以及EMI直接之间的关系。

标签：开关电源；高频变压器；分布电容；模型；抑制措施0 引言随着磁性材料以及开关电源技术的不断发展，变压器逐渐呈现出磁导率高、频率高以及体积小的特点[1～2]。

在变压器高频化、小型化的过程中，一些在低频情况下被忽略的问题越来越重要，如漏感、分布电容。

这些寄生参数在高频下的影响越来越显著，甚至可能严重影响开关电源的性能[3～4]。

应用普通的变压器模型无法描述和解释高频下的一些电路现象，研究变压器高频下的等值模型以及寄生参数对电路的影响机理，以寻求抑制寄生参数的影响，成为该领域广泛关注的重点。

近几年，很多学者对高频变压器的寄生参数、分布参数进行了大量的研究。

本文主要从含分布电容的高频变压器模型、分布电容对电路的影响及其抑制措施三个方面的研究情况进行了总结。

1 考虑分布电容的高频变压器模型目前，国内外研究人员在高频变压器建模方面做了大量的研究，提出各种不同的高频变压器的模型。

这些建模方法主要分为三种，第一种是采用数值分析法，该方法适合于变压器设计但.是需要大量的关于变压器几何尺寸、电磁特性信息；第二种方法，根据变压器的静电学的行为对分布电容建模，该方法是根据静电学的特性，将工作在线性状态下的变压器看做一个端口网络，然后根据端口网络特性来求解相关模型参数，因此该方法具有建模简单，容易理解的特点；第三种方法，通过应用集总等效电容来对变压器的分布电容的物理效应进行建模。

应用该方法建立的模型，其模型中参数的物理意义明确，比较适合从工程角度对变压器进行分析。

变压器的漏感与分布电容影响分析漏感与分布电容对输出波形的影响开关电源变压器一般可以等效成图2-43所示电路。

在图2-43中，Ls为漏感，也可称为分布电感，Cs为分布电容，为励磁电感，R为等效负载电阻。

其中分布电容Cs还应该包括次级线圈等效到初级线圈一侧的分布电容，即次级线圈的分布电容也可以等效到初级线圈回路中。

图2－43 开关电源变压器等效电路设次级线圈的分布电容为C2，等效到初级线圈后的分布电容为C1，则有下面关系式：上式中，Wc2为次级线圈分布电容C2存储的能量，Wc1为C2等效到初级线圈后的分布电容C1存储的能量；U1、U2分别为初、次级线圈的电压，U2 = nU1，n = N2/N1为变压比，N1 、N2分别为初、次级线圈的匝数。

由此可以求得C1为：C1 = n2C2 （2-121）（2-120）式不但可以用于对初、次级线圈分布电容等效电路的换算，同样可以用于对初、次级线圈电路中其它电容等效电路的换算。

所以，C2亦可以是次级线圈电路中的任意电容，C1为C2等效到初级线圈电路中的电容。

由此可以求得图2-43中，变压器的总分布电容Cs为：Cs = Cs1 + C1 = Cs1 +n2C2 （2-122）(2-122)式中，Cs为变压器的总分布电容，Cs1为变压器初级线圈的分布电容；C1为次级线圈电路中总电容C2（包括分布电容与电路中的电容）等效到初级线圈电路中的电容；n = N2/N1为变压比。

图2-43开关变压器的等效电路与一般变压器的等效电路，虽然看起来基本没有区别，但开关变压器的等效电路一般是不能用稳态电路进行分析的；即：图2-43中的等效负载电阻不是一个固定参数，它会随着开关电源的工作状态不断改变。

例如，在反激式开关电源中，当开关管导通时，开关变压器是没有功率输出的，即负载电阻R等于无限大；而对于正激式开关电源，当开关管导通时，开关变压器是有功率输出的，即负载电阻R既不等于无限大，也不等于0 。

小只推荐：变压器的绕制工艺之变压器分布电容
宝剑锋从磨砺出，梅花香自苦寒来；此句是中国流传下来的一句古训，喻为如果想要取得成绩，获取成就，就要能吃苦，勤于锻炼，这样才能靠自己的努力赢得胜利。

各个行业皆是如此。

在电源网论坛里，就存在这样一些人，他们时常能DIY出被网友们称之为的经典设计，出于大家能够共同学习的目的，小编抓住了难得的机会，整理了这些经典帖，供分享学习。

 本文来自心中有冰的精华帖。

--------小编语。

 变压器绕组绕在磁芯骨架上，特别是饶组的层数较多时，不可避免的会产生分布电容，由于变压器工作在高频状态下，那幺这些分布电容对变压器的工作状态将产生非常大的影响，如引起波形产生振荡，EMC变差，变压器发热等。

所以，我们很有必要对变压器的分布电容研究一下，下面我们就对这个分布电容来展开讨论。

 分布电容既然有危害，那幺我们就要设法减小这个分布电容的影响，首先我们来分析下分布电容的组成。

变压器的分布电容主要分为4个部分：绕组匝间电容、层间电容、绕组电容、杂散电容，下面我们来分别介绍。

 首先：绕组匝间电容
 我们知道电容的基本构成就是两块极板，当两块极板加上适当的电压时，极板之间就会产生电场，并储存电荷。

那幺，我们是否可以把变压器相邻两个绕组看成连个极板呢？答案是可以的，这个电容就是绕组匝间电容。

 以变压器初级绕组为例，当直流母线电压加在绕组两端时，各绕组将平均。

多次级高压变压器的分布电容
 引言
 高压变压器的分布参数主要是漏感和分布电容，在高压变压器应用中单次级变压器的分布电容很大，严重影响了电路的工作性能。

为了减小分布电容，将单次级绕组分段绕制后再串联，后接整流和滤波电路。

如果分段后变比依旧很大，那幺在次级匝数依然很多的情况下，分布电容依然较大。

当分布电容不为所用时，只有想方设法减小它。

 本文通过传统绕线和PCB迭绕两种工艺的比较，并采用谐振法测得谐振频率及通过计算得到分布电容，最后以实测波形说明分布电容对电路性能的影响。

1 分布电容产生机理
 在高压变压器中，分布电容由匝间分布电容和层间分布电容构成。

任何。

高频变压器分布电容的测量
张朋朋;高国强;向欣;刘庆想
【期刊名称】《电源技术应用》
【年(卷),期】2009(33)2
【摘要】根据串并联谐振式电容器充电电源中谐振电流正负周期的变化特点，提出一种测量分布电容的方法。

该方法仅需观察充电过程中谐振电流的波形，通过比较各个时间段谐振电流的正负周期值，确定充电电流负谐振周期的最小值，根据该值即可计算出高频变压器中的分布电容值。

最后通过仿真验证了这种测量分布电容方法的准确性。

【总页数】3页(P27-29)
【作者】张朋朋;高国强;向欣;刘庆想
【作者单位】西南交通大学物理科学与技术学院成都610031;西南交通大学电气工程学院成都610031
【正文语种】中文
【中图分类】TM433
【相关文献】
1.高频变压器分布电容研究综述 [J], 杨建华;莫再峰;王成;
2.高频变压器分布电容研究综述 [J], 杨建华;莫再峰;王成
3.高频变压器设计时的漏电感和分布电容的探究 [J], 曹洪武
4.分布电容对高频变压器输出波形的影响分析及其处理 [J], 叶栋;戴瑜兴;贡恩忠;廖鹏
5.分布电容对高频变压器输出波形的影响分析及其处理 [J], 叶栋;戴瑜兴;贡恩忠;廖鹏;
因版权原因，仅展示原文概要，查看原文内容请购买。

高频高压变压器分布电容的分析与处理摘要：本文在分析高频变压器分布参数机理的基础上，以高压直流LCC谐振变换器为实例，阐述了高频高压变压器分布电容对电路带来的不利影响，提出了一种补偿的方法，进行了仿真和实验，提出了高频高压变压器分布电容的测试方法，推导了补偿电感的计算公式，综合使用了两种针对分布电容的处理方法。

实验结果表明该方法的正确性。

关键词：分布电容高频变压器 LCC谐振Analysis and Disposal of Distributed Capacitance in High-Frequencyand High-Voltage TransformerJin Shun1 ， Zheng Guang1 ，Shi Ming2（Xi’an University of Technology, Xi’an 710048, China; Xi’anTelecom, Xi’an 710003,China）Abstract: On the base of analyzing of mechanism of distributed parameters in high frequency transformer, and with a instance of LCC resonant converter , the disadvantage of distributed capacitance in high-frequency and high-voltage transformer is described .A compensation method ,waveforms of both simulation and experiment, and a method of measuring distributed capacitance are given .Formula for calculation compensation inductance is derived .Two methods are used in solving the trouble . Experimental results are presented to verify the theory.Key words: Distributed Capacitance HighFrequency Transformer LCC Resonant1 前言随着(a)(b)图1 (a)变压器磁路中的绕组（b）图1a的等效电路对待该电容的处理主要有两种方法，一是利用，二是补偿。

⾼频变压器绕组绕制⽅式与分布电容⼤⼩分析与计算 随着开关变换器⾼频化，变压器分布电容对电流波形影响越来越明显，由于电容电压不能突变，模态转换时，电容等效为电压源释放电能产⽣尖峰电流。

以下是变压器绕组层间常见的四种绕制⽅法。

下⾯以实际的模型，推导计算C型与Z型绕法分布电容的⼤⼩。

规定沿绕组⾼度⽅向由底端向顶端为ｙ⽅向，初级侧绕组底端电位差为Ｕa，顶端电位差为Ｕb，单层绕组的长度为h，两绕组之间的距离为m。

假设绕组均匀分布，则沿着绕组⾼度⽅向的电位线性变化。

若每⼀层绕组两端压差为Ｕ,则C型绕法任意⾼度ｙ的电位差为： 根据电场能量的密度的定义： 可得，电场能量为： 其中：MLT为绕组平均周长 电场能量等效为: 解得： 同理：根据Z型绕法U(y)=U,为⼀个常数，可以得到等效的原边电容为： 以下是变压器绕组间常见的绕制⽅法： 初级侧绕组与次级侧绕组层间电容的分析不涉及绕组连接处绕制⽅式的问题，因此可以以平⾏板电容器为模型进⾏类⽐[2]。

式中：d：绝缘层厚度 S：两极板正对有效⾯积 h：绕组⾼度 下图左边为⼀般绕制⽅法的，右图为三明治⽅法绕制。

由于三明治绕制⽅法，Ns绕组两边都与Np绕组接触，所以，平⾏板电容正对⾯⾯积S较⼤。

但由于电压分布的原因，分布带内容不是严格的两倍关系。

故三明治绕制绕组间分布电容⼤于⼀般绕制⽅法。

下图为不同绕组布局，分布电容实验数据[1]。

验证了上⽂理论分析。

结论： 1、因为C型层间电压差数学关系，C型绕制分布电容⽐Z型绕制⼤。

2、将线圈匝数分为相等的n等分，相邻匝间的电压差为原来的1/n。

3、累进式绕法减⼩绕组分布电容的效果最佳参考⽂献： [1] 赵志英等.⾼频变压器分布电容的影响因素分析[J].中国电机⼯程学报，2008，28(9)：55-60 [2] 杨欢等.⾼频变压器分布电容的影响因素分析[J].⼭西⼤学学报，2019，42(3):576-583。

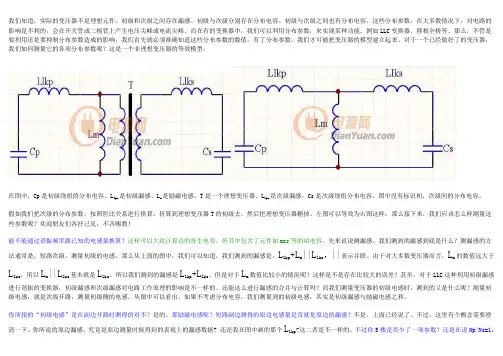
我们知道，实际的变压器不是理想元件。

初级和次级之间存在漏感、初级与次级分别存在分布电容、初级与次级之间也有分布电容。

这些分布参数，在大多数情况下，对电路的影响是不利的，会在开关管或二极管上产生电压尖峰或电流尖峰。

而在有的变换器中，我们可以利用分布参数，来实现某种功能。

例如LLC变换器、移相全桥等。

那么，不管是要利用还是要抑制分布参数造成的影响，我们首先就必须准确知道这些分布参数的数值，有了分布参数，我们才可能把变压器的模型建立起来。

对于一个已经做好了的变压器，我们如何测量它的各项分布参数呢？这是一个非理想变压器的等效模型：在图中，Cp是初级绕组的分布电容、L lkp是初级漏感、L m是励磁电感、T是一个理想变压器、L lks是次级漏感，Cs是次级绕组分布电容。

图中没有标识初、次级间的分布电容。

假如我们把次级的分布参数，按照匝比关系进行换算，折算到理想变压器T的初级去。

然后把理想变压器删掉。

左图可以等效为右图这样：那么接下来，我们应该怎么样测量这些参数呢？欢迎朋友们各抒己见，不吝赐教！能不能通过谐振频率跟已知的电感量换算？这样可以大致计算总的寄生电容，但其中包含了元件如mos等的结电容。

先来说说测漏感。

我们测到的漏感到底是什么？测漏感的方法通常是，短路次级，测量初级的电感。

那么从上面的图中，我们可以知道，我们测到的漏感是：L lkp+L m||L lks，||表示并联。

由于对大多数变压器而言，L m的数值远大于L lks，所以L m||L lks基本就是L lks。

所以我们测到的漏感是L lkp+L lks。

但是对于L m数值比较小的情况呢？这样是不是存在比较大的误差？甚至，对于LLC这种利用初级漏感进行谐振的变换器，初级漏感和次级漏感对电路工作原理的影响是不一样的。

还能这么进行漏感的合并与计算吗？而我们测量变压器的初级电感时，测到的又是什么呢？测量初级电感，就是次级开路，测量初级侧的电感。

从图中可以看出，如果不考虑分布电容，我们测量到的初级电感，其实是初级漏感与励磁电感之和。