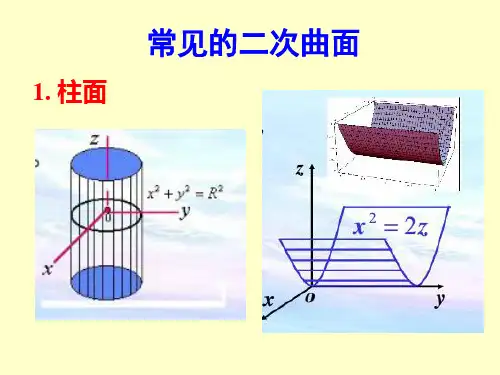
时与 投影
• 若平行于坐标轴直线穿过区域 时与它边
界曲面S相交多于两点,可把
分成若干部分,
再求和.
第7页
例1. 计算三重积分 xdxdydz, 其中 为三个坐标
面及平面 x 2 y z 1 所围成闭区域 .
解 ( x, y, z) | 0 z 1 x 2 y,( x, y) Dxy
{( x, y, z) | x2 +y2 +z2 R2 ,x2 +y2 +(z-R)2 R2 }.
解法一:利用柱面坐标
解法二:利用球面坐标.
把的边界曲面方程化为球面坐标方程
r=R,r=2Rcos
第24页
它们的交线为圆
因此的边界曲面由
r=R
=
3
r=R
(0
3
)与 r=2Rcos
组成,于是
(
3
2
例3.5计算I zdv,其中由曲面z= 4-x2-y2
与x2 y2 3z所围成。
第19页
(2) 利用球面坐标计算三重积分(注意此处两个角与书上表示
符号刚好相反.)
设 M (x, y, z) R3, 其柱坐标为(, , z), 令 OM r, ZOM , 则(r, , ) 就称为点M 球坐标. z
第12页
三、三重积分变量替换
定理: 设f ( x, y, z)在闭域 上连续 , 作变换:
满足
x x(u, v, w)
T
:
y
y(u, v,
w)
z z(u, v, w)
(u, v, w) (*)
(1) x(u, v, w) , y(u, v, w), z(u, v, w) 在 上具有连续的偏导数;
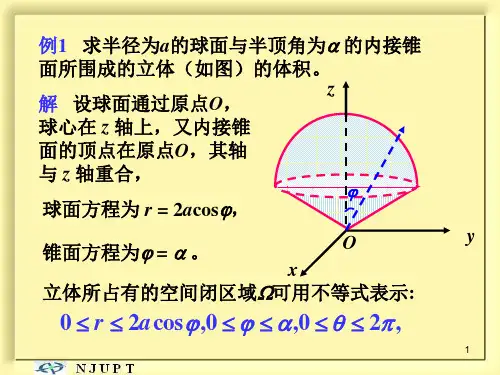

![[理学]三重积分习题课ppt课件](https://uimg.taocdn.com/4ee4da0b856a561253d36fa0.webp)