(完整版)最全圆周运动模型

圆周运动的几个模型一、水平方向的圆盘模型1． 如图1.01所示，水平转盘上放有质量为m 的物块，当物块到转轴的距离为r 时，连接物块和转轴的绳刚好被拉直（绳上张力为零）。

物体和转盘间最大静摩擦力是其正压力的μ倍，求：（1）当转盘的角速度时，细绳的拉力。

（2）当转盘的角速度时，细绳的拉力。

图2.01解析：设转动过程中物体与盘间恰好达到最大静摩擦力时转动的角速度为，则，解得。

（1）因为，所以物体所需向心力小于物体与盘间的最大摩擦力，则物与盘间还未到最大静摩擦力，细绳的拉力仍为0，即。

（2）因为，所以物体所需向心力大于物与盘间的最大静摩擦力，则细绳将对物体施加拉力，由牛顿的第二定律得：，解得。

2． 如图2.02所示，在匀速转动的圆盘上，沿直径方向上放置以细线相连的A 、B 两个小物块。

A 的质量为，离轴心，B 的质量为，离轴心，A 、B 与盘面间相互作用的摩擦力最大值为其重力的0.5倍，试求：（1）当圆盘转动的角速度为多少时，细线上开始出现张力？角速度为多大？（）图2.02（1）当圆盘转动的角速度为多少时，细线上开始出现张力？（2）欲使A、B与盘面间不发生相对滑动，则圆盘转动的最大角速度为多大？（）解析：（1）较小时，A、B均由静摩擦力充当向心力，增大，可知，它们受到的静摩擦力也增大，而，所以A受到的静摩擦力先达到最大值。

再增大，AB间绳子开始受到拉力。

由，得：（2）达到后，再增加，B增大的向心力靠增加拉力及摩擦力共同来提供，A增大的向心力靠增加拉力来提供，由于A增大的向心力超过B增加的向心力，再增加，B所受摩擦力逐渐减小，直到为零，如再增加，B所受的摩擦力就反向，直到达最大静摩擦力。

如再增加，就不能维持匀速圆周运动了，A、B就在圆盘上滑动起来。

设此时角速度为，绳中张力为，对A、B受力分析：对A有对B有联立解得：3．如图2.03所示，两个相同材料制成的靠摩擦传动的轮A和轮B水平放置，两轮半径，当主动轮A匀速转动时，在A轮边缘上放置的小木块恰能相对静止在A轮边缘上。

定理
向心加速度公式 $a_{n} = frac{v^{2}}{r}$，其中 $a_{n}$ 是向心加速度，$v$ 是 物体的线速度，$r$ 是圆周运动的半径。
实例分析
实例1 实例2
04
水平面内的圆周运动
定义与特点
定义
特点
公式与定理
公式
定理
实例分析
01
火车转弯
02 自行车轮转动
03 离心机
05
实例分析
实例1
实例2 实例3
THANKS
感谢观看
VS
详细描述
地球自转是典型的匀速圆周运动实例，地 球围绕自己的轴线做周期性转动，形成了 昼夜交替的现象。钟表指针的转动也是匀 速圆周运动的实例，秒针、分针和时针均 以恒定的角速度转动。旋转木马也是匀速 圆周运动的实例，木马围绕中心轴做匀速 转动，乘客在木马上感受到的力是向心力。
02
变速圆周运动
定义与特点
线速度定义为质点到圆心的距离与通过该质点的圆弧长度的比值，记作v。角速度定义为单位时间内转过的角度， 记作ω。周期T是完成一次圆周运动所需的时间，频率f是一秒内完成的圆周运动次数，转速n是一秒内转过的圈 数。这些公式和定理是描述匀速圆周运动的基本工具。
实例分析
总结词
匀速圆周运动的实例包括地球自转、钟 表指针的转动、旋转木马等。
公式与定理
01
向心加速度公式
02
离心加速度公式
03向心力公式04 Nhomakorabea离心力公式
实例分析
匀速圆周运动 变速圆周运动
03
竖直面内的圆周运动
定义与特点
定义
特点
物体受到重力和绳子的拉力作用，拉 力方向始终沿着圆周的切线方向，重 力方向始终竖直向下。

F合
mg
tan
F心
F心
mv2 r
mw2r
解得：
v gr
tan
w g
tan r
规律：稳定状态下，小球所处的位置越高，半径r越
大，角速度越小，线速度越大，而小球受到的支持
力和向心力并不随位置六的种圆变周运化动而模型变化。
4
三、火车转弯模型：
六种圆周运动模型
5
四、汽车过桥模型：
F向
ma
ห้องสมุดไป่ตู้
mv2 R
F向
ma
mv2 R
FN
G mv2 R
六种圆周运动模型
6
五、轻绳模型
1、安全通过最高点的临界条件:
v临 = gR
2、对最高点分析：
v＞
gR
：绳子或外轨道对物体的弹力:
v2 F m G
R
方向竖直向下
v = g R :绳子或外轨道对物体的弹力:F=0
v＜ gR:物体不能过最高点！！！
v = g R 是物体所六种受圆周弹运力动模方型 向变化的临界速度。 7
六种圆周运动模型分析
六种圆周运动模型
1
一、圆盘模型：
F合f F心mr2vm2w r
当f最大值时： f mg 线速度有最大值：v gr
g
角速度有最大值：w r
六种圆周运动模型
2
二、圆锥摆模型： 由拉力F和重力G的合力提供向心力
六种圆周运动模型
3
倒置圆锥摆模型:
1.如果内壁光滑，由重力和支持力的合力提供向心力

F向
mamv2 R
FN
Gmv2 R
最新版整理ppt
6
五、轻绳模型
1、安全通过最高点的临界条件:
v临 = gR
2、对最高点分析：
v＞
gR ：绳子或外轨道对物体的弹力:
v2 F m G
R
方向竖直向下
v = gR :绳子或外轨道对物体的弹力:F=0
v＜ gR:物体不能过最高点！！！
v = g R 是物体所最受新版弹整力理pp方t 向变化的临界速度。 7
8
六种圆周运动模型分析
最新版整理ppt
1
一、圆盘模型：
F合f F心m r2vm2w r
当f最大值时： f mg
线速度有最大值：v gr 角速度有最大值：w g
r
最新版整理ppt
2
二、圆锥摆模型： 由拉力F和重力G的合力提供向心力
最新版整理ppt
3
倒置圆锥摆模型:
1.如果内壁光滑，由重力和支持力的合力提供向心力
六、轻杆模型
1、安全通过最高点的临界条件:
v临 = gR
2、对最高点分析：
v＞
gR
：绳子或轨道对物体的弹力:
F
v2 m G
R
方向竖直向下
v = gR :轻杆或管道对物体的弹力:F=0
v＜ gR:轻杆或管道对物体的弹力:
v2 FN Gm R
方向竖直向上
ቤተ መጻሕፍቲ ባይዱ
v = g R 是物体所最新受版弹整理力pp方t 向变化的临界速度。
F合tm angF心 F心mrv2 mw2r
解得：
v gr
tan
w g
tan r
规律：稳定状态下，小球所处的位置越高，半径r越

圆周运动的三种模型一、圆锥摆模型：如图所示：摆球的质量为m，摆线长度为L ，摆动后摆球做圆周运动，摆线与竖直方向成θ角，对小球受力分析，正交分法解得：竖直方向：水平方向：F X=最终得F合=。

用力的合成法得F合=。

半径r=，圆周运动F向==，由F合=F向可得V=，ω=圆锥摆是物理学中一个基本模型，许多现象都含有这个模型。

分析方法同样适用自行车，摩托车，火车转弯，飞机在水平面内做匀速圆周飞行等在水平面内的匀速圆周运动的问题。

共同点是由重力和弹力的合力提供向心力，向心力方向水平。

1、小球在半径为R 的光滑半球内做水平面内的匀速圆周运动，试分析图中θ（小球与半球球心连线跟竖直方向的夹角）与线速度V ，周期T 的关系。

（小球的半径远小于R）2、如图所示，用一根长为l＝1m的细线，一端系一质量为m＝1kg的小球（可视为质点），另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝37°，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T。

求（取g＝10m/s2，结果可用根式表示）：（1）若要小球离开锥面，则小球的角速度ω0至少为多大？（2）若细线与竖直方向的夹角为60°，则小球的角速度ω＇为多大？二．轻绳模型（一）轻绳模型的特点：1. 轻绳的质量和重力不计；2. 只能产生和承受沿绳方向的拉力；（二）轻绳模型在圆周运动中的应用小球在绳的拉力作用下在竖直平面内做圆周运动的临界问题：1. 临界条件：小球通过最高点，绳子对小球刚好没有力的作用，由重力提供向心力： = ，v 临界 =2. 小球能通过最高点的条件： v v 临界（此时，绳子对球产生 力）3. 不能通过最高点的条件： v v 临界 （实际上小球还没有到最高点时，就脱离了轨道）练习：质量为m 的小球在竖直平面内的圆形轨道的内侧运动，经过最高点而不脱离轨道的临界速度为v ，当小球以2v 的速度经过最高点时，对轨道的压力是（ ）A . 0 B. mg C .3mg D 5mg三．轻杆模型：(一)轻杆模型的特点：1.轻杆的质量和重力不计；2.能产生和承受各方向的拉力和压力(二)轻杆模型在圆周运动中的应用轻杆的一端连着一个小球在竖直平面内做圆周运动，小球通过最高点时，轻杆对小球产生弹力的情况：1. 小球能通过最高点的最小速度v= ，此时轻杆对小球的作用力N= （ N 为 力）2. 当 =R v m 2临界（ 轻杆对小球的作用力N= 0 ），gR v 临界3 当 （即0<v< v 临界）时，有 =Rv m 2（ 轻杆对小球的作用力N 为 力）4 当（即v>v 临界）时，有 =R v m 2（轻杆对小球的作用力N 为 力） 练习：半径为R=0.5m 的管状轨道，有一质量为m=3kg 的小球在管状轨道内部做圆周运动，通过最高点时小球的速率是2m/s ，g=10m/s2 ，则（ ）A. 外轨道受到24N 的压力B. 外轨道受到6N 的压力C. 内轨道受到24N 的压力D. 内轨道受到 6N 的压力一．轻绳模型（一）轻绳模型的特点：1. 轻绳的质量和重力不计；2. 只能产生和承受沿绳方向的拉力；（二）轻绳模型在圆周运动中的应用小球在绳的拉力作用下在竖直平面内做圆周运动的临界问题：1. 临界条件：小球通过最高点，绳子对小球刚好没有力的作用，由重力提供向心力：2. 小球能通过最高点的条件：（当时，绳子对球产生拉力）3. 不能通过最高点的条件：（实际上小球还没有到最高点时，就脱离了轨道）例：质量为m的小球在竖直平面内的圆形轨道的内侧运动，经过最高点而不脱离轨道的临界速度为v ，当小球以2v的速度经过最高点时，对轨道的压力是（）A . 0 B. mg C .3mg D 5mg分析：内侧轨道只能对小球产生向下的压力，其作用效果同轻绳一样，所以其本质是轻绳模型当小球经过最高点的临界速度为v ，则当小球以2v的速度经过最高点时，轨道对小球产生了一个向下的压力N ，则因为所以根据牛顿第三定律，小球对轨道压力的大小也是，故选c.1.轻杆的质量和重力不计；2.能产生和承受各方向的拉力和压力(二)轻杆模型在圆周运动中的应用轻杆的一端连着一个小球在竖直平面内做圆周运动，小球通过最高点时，轻杆对小球产生弹力的情况：1. 小球能通过最高点的临界条件：v=0 ，N=mg （N为支持力）2. 当时，有（N为支持力）3 当时，有（N=0 ）4 当时，有（N 为拉力）例：半径为R=0.5m 的管状轨道，有一质量为m=3kg的小球在管状轨道内部做圆周运动，通过最高点时小球的速率是2m/s ，g=10m/s2 ，则（）A. 外轨道受到24N的压力B. 外轨道受到6N的压力C. 内轨道受到24N 的压力D. 内轨道受到6N的压力分析：管状轨道对小球既有支持力又有压力，所以其本质属于杆模型：当小球到最高点轨道对其作用力为零时：有则， =>2m/s所以，内轨道对小球有向上的支持力，则有代入数值得：N=6N根据牛顿第三定律，小球对内轨道有向下的压力大小也为6N ，故选D三．圆锥摆模型：圆锥摆模型在圆周运动中的应用：如图所示：摆球的质量为m，摆线长度为L ，摆动后摆线与竖直方向成θ角，则分析：摆球在水平面上做匀速圆周运动，加速度必定指向圆心，依据牛顿第二定律，对摆球受力分析，得：圆锥摆是物理学中一个基本模型，许多现象都含有这个模型。

圆周运动模型一、匀速圆周运动模型 1．随盘匀速转动模型1．如图，小物体m 与圆盘保持相对静止，随盘一起做匀速圆周运动，则物体的受力情况是： A ．受重力、支持力、静摩擦力和向心力的作用 B ．摩擦力的方向始终指向圆心O C ．重力和支持力是一对平衡力 D ．摩擦力是使物体做匀速圆周运动的向心力 2． 如图所示，质量为m 的小物体系在轻绳的一端，轻绳的另一端固定在转轴上。

轻绳长度为L 。

现在使物体在光滑水平支持面上与圆盘相对静止地以角速度 做匀速圆周运动，求：（1）物体运动一周所用的时间T ；（2）绳子对物体的拉力。

3、如图所示，MN 为水平放置的光滑圆盘，半径为1.0m ，其中心O 处有一个小孔，穿过小孔的细绳两端各系一小球A 和B ，A 、B 两球的质量相等。

圆盘上的小球A 作匀速圆周运动。

问（1）当A 球的轨道半径为0.20m 时，它的角速度是多大才能维持B 球静止？（2）若将前一问求得的角速度减半，怎样做才能使A 作圆周运动时B 球仍能保持静止？4、如图4所示，a 、b 、c 三物体放在旋转水平圆台上,它们与圆台间的动摩擦因数均相同，已知a 的质量为2m ，b 和c 的质量均为m ，a 、b 离轴距离为R ，c 离轴距离为2R 。

当圆台转动时,三物均没有打滑，则：（设最大静摩擦力等于滑动摩擦力）（ ）A.这时c 的向心加速度最大 B ．这时b 物体受的摩擦力最小C.若逐步增大圆台转速，c 比b 先滑动 D ．若逐步增大圆台转速，b 比a 先滑动5、如右图所示，某游乐场有一水上转台，可在水平面内匀速转动，沿半径方向面对面手拉手坐着甲、乙两个小孩，假设两小孩的质量相等，他们与盘间的动摩擦因数相同，当圆盘转速加快到两小孩刚好还未发生滑动时，某一时刻两小孩突然松手，则两小孩的运动情况是( ) A ．两小孩均沿切线方向滑出后落入水中 B ．两小孩均沿半径方向滑出后落入水中C ．两小孩仍随圆盘一起做匀速圆周运动，不会发生滑动而落入水中D ．甲仍随圆盘一起做匀速圆周运动，乙发生滑动最终落入水中6、线段OB=AB ，A 、B 两球质量相等，它们绕O 点在光滑的水平面上以相同的角速度转动时，如图4所示，两段线拉力之比T AB ：T OB ＝______。

F
N
v m g tan m R
当v 当v
得
v gR tan
F
gR tan
时，外轨对轮缘有侧向压力 时，内轨对轮缘有侧向压力
gR tan
h
θ m g
2、汽车过弯道
汽车在水平地面上转弯是什么力提供向心力的呢?
FN Ff
O
mg
汽车在水平路面上转弯所 需要的向心力来源:汽车侧 向所受的静摩擦力。
轨道提供支 持力,绳子提 供拉力。
② 杆和双轨模型
能过最高点的临界条件:
当FN mg时 v
v临界＝0
FN mg
讨论
当速度v > gr 时, 杆对小球是拉力;
当速度v < gr 时, 杆对小球是支持力;
v FN m g m r
2
2
当速度v = gr 时, 杆对小球无作用力。
v m gHale Waihona Puke FN m r圆周运动模型
动力学问题解题步骤
• 1、受力分析： 顺序：重力—接触力（支持力、压力、拉力）—摩 擦力（静摩擦力、滑动摩擦力） • 2、求合力：平行四边形、正交分解法 • 3、根据运动状态列方程： • 静止或匀速直线运动：F合=0，x=vt 1 2 • 匀变速直线运动： F合=ma，vt v0 at x v0t 2 at 2 2 v • 匀速圆周运动： F合=Fn=man= m m 2 R m R T R • 非匀速圆周运动：正交分解 • 切向： F切合=ma切n
2
FN = G
G
航天器中的失重现象
FN
v Mg - FN= m R
2
mg
v2 FN = m g R

越大
（C）使物体A的转动半径变小一些，在转动过程中半径会随时
稳定
（D）以上说法都不正确
O A
第22页/共35页
B O′
水平转盘：例6、如图，细绳一端系着质量M=0.6千克的物体，静止在水平面，另一 端通过光滑小孔吊着质量m=0.3千克的物体，M的中点与圆孔距离为0.2米，并知M 和水平面的最大静摩擦力为2牛，现使此平面绕中心轴线转动，问角速度在什么范 围m会处于静止状态？(g取10米/秒2)
钢丝绳下端可挂载重物，以便在车间内移动物体．本题中铸件开始做匀速直线运动， 行车突然停止，铸件的速度在瞬间内不变，钢丝绳的悬点固定，铸件在竖直平面内 做小幅度的圆周运动．
第8页/共35页
• 变式训练2—1 如图所示，一根绳长l
＝1m，上端系在滑轮的轴上，下端拴
一质量为m＝1kg的物体，滑轮与物
体一起以2m/s的速度匀速向右运动，
第14页/共35页
传送带模型：例1、如图所示，两个轮通过皮带传动
，设皮带与轮之间不打滑，A为半径为R的O1轮缘上一 点，B、C为半径为2R的O2轮缘和轮上的点， O2C=2R/3，当皮带轮转动时，A、B、C三点的角度 之比:
ωA : ωB : ωC = 2 : 1 : 1 ; A、B、C三点的线速度之比vA : vB : vC = 3 : 3 : 1 ; 及三点的向心加速度之比aA : aB: aC = 6 : 3 : 1 .
线速度即小球运动的合速度，小球位置越低，势能转化为动能就越多，速 度也就越大，C正确.
小球在最低位置时速度为水平速度，由于小球做圆周运动
，绳拉力与球重力的合力提供向心力，即 D错误．
v2 T mg m
R
第24页/共35页

三维设计章末小结：专题冲关 p30页第3题
3．如图2－7所示，OM＝MN＝R。两个 小球M、N质量都是m，a、b为水平 轻绳，且沿同一条半径。两小球正随 水平圆盘以角速度ω匀速同步转动。 小球和圆盘间的摩擦力可以不计。求： (1)绳b对小球N的拉力大小； (2)绳a对小球M的拉力大小。
解析：(1)对球N，受力如图甲所示，其做圆周运动的半径为 2R，根据牛顿第二定律有
平抛+圆周运动模型
作业： 1、完成三维设计及课时跟踪训练； 2、整理错题集并做好第一次段考的复习，段考之后 将对每个人的笔记本（包括错题集）、三维设计进行 一次大检查，尤其是物理平时不交作业的并且成绩不 理想的。
Fb＝mω2·2R＝2mω2R。 (2)对球M，受力如图乙所示，其做圆周运动的半径为R，根 据牛顿第二定律有 Fa－Fb′＝mω2R Fb＝Fb′ 解得Fa＝Fb′＋mω2R＝3mω2R。 答案：(1)2mω2R (2)3mω2R
课时跟踪训练质量检测（二）p101页
答案：A
F拉
l
F向
mg
答案：CD
匀速圆周运动的常见模型分类
1.汽车在水平路面上转弯
N
F
G
向心力F由车轮与路面间的静摩 擦力来提供。如果转弯时汽车速 度过快，则这个静摩擦力不足以 提供汽车所需的向心力，汽车就 容易滑出路面，造成交通事故。
2.汽车（或火车）在倾斜路面上转弯
mg tan m v临2
R
v临
gR tan
(1)当v等于 gR tan时不受摩擦力（或压力）
供，图 2－1 所示为赛车做圆周运动的后视图(赛车正垂直
纸面向里运动)。赛车以最大速度 vmax 行驶时，地面对赛车的 摩擦力为最大静摩擦力 fmax。受力分析如图所示，利用正交分 解法列方程

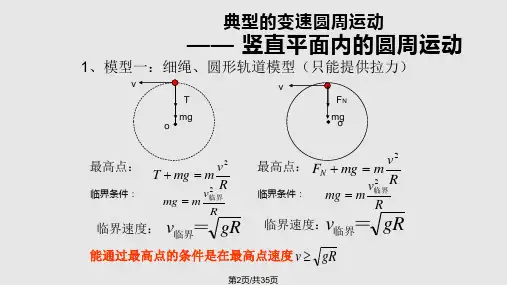
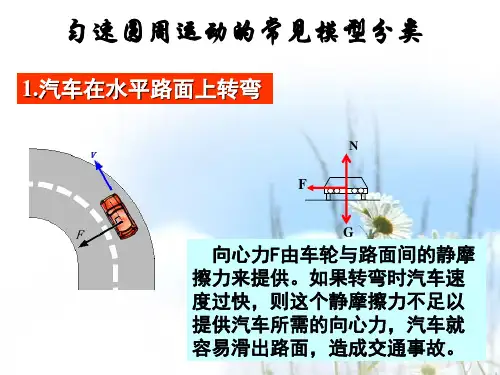
高一物理生活中的圆周运动以及模型高一物理生活中的圆周运动以及模型圆周运动在我们的生活中无处不在。

从地球公转的运动，到车轮不断旋转的场景，都是我们日常所接触到的圆周运动案例。

那么，我们应该如何通过模型来更好地了解圆周运动呢？在本文中，将为大家详细介绍圆周运动及其模型。

一、圆周运动的基本概念圆周运动是指一个物体绕着同心圆运动的过程。

其中，物体的运动轨迹为圆周，圆心为轴心。

在物体绕着同心圆运动的过程中，可以比较清晰地看到运动的周期性、旋转方向、角速度等特征。

二、圆周运动的公式对于圆周运动，我们可以通过以下公式来进行计算1. 圆周运动的速度公式：v = 2πr÷T其中，v为速度，r为圆周半径，T为周期2. 圆周运动的角速度公式：ω = 2π÷T其中，ω为角速度，T为周期3. 圆周运动的向心加速度公式：a = v²÷r 或a = ω²r其中，a为向心加速度，v为速度，r为圆周半径，ω为角速度三、圆周运动的模型1. 均匀圆周运动模型均匀圆周运动指的是物体沿着半径相等且时间相等的圆弧运动的过程。

在这种情况下，物体在同一段时间内所旋转的角度相同，角速度不变，速度也不变。

因此，我们可以通过简单的公式计算出速度、角速度等。

2. 非均匀圆周运动模型非均匀圆周运动指的是物体沿着半径不等或时间不等的圆弧运动的过程。

由于半径、时间的不同，物体在相同时间内所旋转的角度就会不同，角速度也会发生变化。

因此，我们需要更加复杂的公式来计算速度、角速度等。

四、圆周运动的应用1. 摩托车甩尾摩托车甩尾是一种基于圆周运动的极限运动。

通过使摩托车侧滑时绕圆周运动，骑手可以通过调整路线，达到加速或者刹车等目的。

2. 银河系环形摆动在银河系中，恒星和气体等物体绕着银河系中心旋转，这就是一种基于圆周运动的现象。

而由于各种因素的干扰，这种圆周运动会产生摆动，产生银河系的环形构造。

这为我们研究宇宙结构构造提供了重要线索。

w g
tan r
规律：稳定状态下，小球所处的位置越高，半径r越 大，角速度越小，线速度越大，而小球受到的支持 力和向心力并不随位置的变化而变化。
三、火车转弯模型：
四、汽车过桥模型：
F向
ma
mv2 R
FN
G
mv2 R
F向
ma
mv2 R
五、轻绳模型
1、安全通过最高点的临界条件:
v临 = gR
2、对最高点分析：
F
v2 m G
R
方向竖直向下
v = g R :轻杆或管道对物体的弹力:F=0
v＜ g R:轻杆或管道对物体的弹力:
FN
G m v2 R
方向竖直向上
v = g R 是物体所受弹力方向变化的临界速度。
结束语
谢谢大家聆听！！！
8
•、圆盘模型：
F合f F心mr2vmw 2r
当f最大值时： f mg 线速度有最大值：v gr 角速度有最大值：w g
r
二、圆锥摆模型： 由拉力F和重力G的合力提供向心力
倒置圆锥摆模型:
1.如果内壁光滑，由重力和支持力的合力提供向心力
F合
mg
tanΒιβλιοθήκη F心F心mv2 r
mw2r
解得：
v gr
tan
v＞
gR
：绳子或外轨道对物体的弹力:
v2 F m G
R
方向竖直向下
v = g R :绳子或外轨道对物体的弹力:F=0
v＜ g R:物体不能过最高点！！！
v = g R 是物体所受弹力方向变化的临界速度。
六、轻杆模型
1、安全通过最高点的临界条件:
v临 = gR
2、对最高点分析：

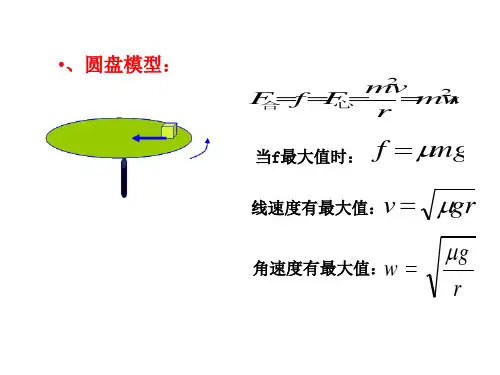
圆周运动模型解题思路①明确研究对象进⾏受⼒分析画出受⼒示意图②分析向⼼为来源③列⽅程in aim Fmuim筘mwo④解⽅程⽔平圆周模型-圆盘模型gwiv问缓慢增机求滑块相对滑动的⼼弱⼥䳸f充当向⼼⼒finnair wi閒fif当ffmaing时W达到最⼤ynmgmwr w⼈越⼩r越⼤越容易滑动与m⽆关0⽐ 时滑块未滑动癌-1⾼⼆muir⼼愿时相对滑动所需知后ing例已知A13C质量分别为mnmn meAǒc们半径分别为r r2⼦从相同0恰好相对圆盘静⽌求A13受到的fEt国国对ciyimcgmuizr⽐㯚Ii MA Wir fimBW ir2半径为r A13之间从⼀13与圆盘之间㥘遯13谁先滑动0W A从啊MAW irtB Mziniig m gHmng mBg ui i临界值Wi㦡Wpi㦡随着必IMA 喖w_w A先滑州州3WFWB⼀起滑州以3WPWB13先AB⼀起3已知物块质量为in r判断绳中是否有拉⼒cowmgmw ir w㾚0was fjnuir TOrǖw_w Fīymgmwr4已知Mmg W RA RB闻绳内何时产⽣⼒何时滑动同侧0W MMg mw in WB原A BOW WB静提供向⼼⼒绳⽆拉⼒国国Wiwa Wa绳产⽣拉⼒B Mmg t Em winA静⼀Em winW_w A⻢上滑动BMgtEmwirBAmg F mw in⺕15已知A13质量分别为m M动摩擦因 13相对圆盘静⽌半径为r求⼉的取值范围cow对A F mgir邮对13⽐较⼩时t sf T f MWrmg MMg Mwm ir uift A国当⼤0时Ta EM wirW愿was揹离圆⼼w_w f指向圆⼼⽐较⼤时if If MuirmgtyMg Mwmiwl sfp wm in WE Wmaxi6AW愿Biwi愿异侧ow加㜾B先临界①0WEW A13均为 绳内⽆拉⼒照照此⼼以B pig不够绳内有拉⼒撤T 对B T国对AT tpng m hn Ttf静MA uniwi iti TT if静减⼩1先向内减为0再向外增⼤1豳T之后AT f静⼆mini㓥静Mng时A临界T png m in17已知mr MN弹簧劲度系数为k物块恰不滑动求愿⻓1 cow W瘵Wcw义⼼压缩im ymg kil rkmairwno tk拉伸Nmgtkl nl mwr⼆圆锥摆模型扃mgtanoagtanoLim Wriiiw等⻓圆锥摆L 定_F mgtanQmwl si no LniW ⺦品等⻓圆锥摆转动速度过快甩得越⾼等⾼圆锥摆h 定_tan ⽉卡W 原等⾼圆锥摆w 下㜀等IĀh⽐过⼤h 减⼩⼩球会⻜起来go____W 从0增⼤a ⼀定有⼒b 不⼀定有⼒T asintmg的定值T acos 0⼗万muir万增⼤三漏⽃模型i1三器咔a㵿mgǚtan卡让丽对于同⼀漏⽃⼼不蕊___1向⼼加速度都相同2都相同为后相同了若⼼则内Not你从碗底到碗⼝逐渐减⼩让不半球形碗R固定不变近⼼离⼼屩ME灜⼀指向圆⼼的合⼒法向⼒则证姆屩⼆灜圆周运动阼咔F㟐㳡⽊屩灜离⼼运动V不够屩1赢近⼼运动洗⾐机脱⽔筒四过弯模型汽⻋⽔平转弯0最⼤值是多少if_意囌5囑喈jumgm 等Vmihugrit rt 越容易侧滑⽕⻋转弯_䑉mg与1元的合⼒1鬺哶可tan1⾼⼆mgtanmiFiliT ano若Plant 则mgtan 孙于所需的⼒mg外轨施加向内的压⼒若以Tt 则mgtan 挝⼤内轨施加向外的⽀持⼒I竖直圆周模型⼀绳模型佯轨m最⾼点Ttmgm毕选重v r当我0时要恰好通过最⾼点mgm下0原oi若想完成完整的圆周运动则到最⾼点速度⾄少为原最低点T mg__m憴重单轨模型最⾼点Fnitmg喋i若想完成完整的圆周运动则到最⾼点速度⾄少为原侃0最低点Firing暩最⾼点F0图像绳对⼩球作⽤⼒FnEm E mgmgmO b V2⼆杆模型双轨m A最⾼点速度从0开始逐渐增⼤R籲mg与流的合⼒屫啥当⻓较⼩时mg1元㗳以越⼤1元越⼩当11元0时mgm等红厅⼦当以较⼤时mg1元哶以越⼤Fi越⼤最低点杆只能提供拉⼒FN mg my双轨模型最⾼点当⻓较⼩时内轨提供向上的1元当阮0时轨道恰⽆作⽤⼒让原当以较⼤时外轨提供向下的信最低点外轨提供向上的1元最⾼点F0图像杆对⼩球作⽤⼒i V2的时V3b时F mE mg F mE mgmg咔0b702三过⽊雕型mg F mil 最⾼点失重若V 直增⼤则所需向⼼⼒增⼤FN Img 安全⾏驶速度以后若让原做平抛运动若以后汽⻋抵达桥顶前斜抛⻜出i Firing 啱超重汽⻋过凹形桥时轮胎所受压⼒⼤于重⼒lmg 若以FA 有爆胎⻛险四斜⾯圆周模型光滑斜⾯最⾼点受⼒分析mgs in 0-T 唥当mgsint 咔即019sinai 时恰能通过最⾼点。

圆周运动中的临界问题一.两种模型:(1)轻绳模型：一轻绳系一小球在竖直平面内做圆周运动.小球能到达最高点(刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力）. 类此模型：竖直平面内的内轨道(2)轻杆模型：一轻杆系一小球在竖直平面内做圆周运动，小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 . （杆既可以提供拉力，也可提供支持力或侧向力.） ①当v ＝0 时，杆对小球的支持力 小球的重力； ②当0<v <gr 时，杆对小球的支持力于小球的重力；③当v＝gr 时，杆对小球的支持力 于零； ④当v >gr 时，杆对小球提供 力. 类此模型：竖直平面内的管轨道.1、圆周运动中绳模型的应用 【例题1】长L ＝0.5m 的细绳拴着小水桶绕固定轴在竖直平面内转动，筒中有质量m ＝0.5Kg 的水，问：（1）在最高点时，水不流出的最小速度是多少？（2）在最高点时，若速度v ＝3m/s ，水对筒底的压力多大？【训练1】游乐园里过山车原理的示意图如图所示。

设过山车的总质量为m ，由静止从高为h 的斜轨顶端A 点开始下滑，到半径为r 的圆形轨道最高点B 时恰好对轨道无压力。

求在圆形轨道最高点B 时的速度大小。

【训练2】．杂技演员在做水流星表演时，用绳系着装有水的水桶，在竖直平面内做圆周运动，若水的质量m ＝0．5 kg ，绳长l=60cm ，求：(1)最高点水不流出的最小速率。

(2)水在最高点速率v ＝3 m ／s 时，水对桶底的压力．2、圆周运动中的杆模型的应用【例题2】一根长l ＝0.625 m 的细杆，一端拴一质量m=0.4 kg 的小球，使其在竖直平面内绕绳的另一端做圆周运动，求：(1)小球通过最高点时的最小速度；(2)若小球以速度v 1=3.0m ／s 通过圆周最高点时，杆对小球的作用力拉力多大?方向如何？vR 【训练3】如图所示，长为L 的轻杆一端有一个质量为m 的小球，另一端有光滑的固定轴O ，现给球一初速度，使球和杆一起绕O 轴在竖直平面内转动，不计空气阻力，则（ ） A.小球到达最高点的速度必须大于gLB .小球到达最高点的速度可能为0 C.小球到达最高点受杆的作用力一定为拉力 D.小球到达最高点受杆的作用力一定为支持力【训练4】如图所示，在竖直平面内有一内径为d 的光滑圆管弯曲而成的环形轨道，环形轨道半径R 远远大于d ，有一质量为m 的小球，直径略小于d ，可在圆管中做圆周运动。

六种圆周运动模型
XX,a click to unlimited possibilities
汇报人：XX
目录
01 匀 速 圆 周 运 动
02 变 速 圆 周 运 动
03 斜 抛 圆 周 运 动
04 竖 直 上 抛 圆 周 运 动
05 自 由 落 体 圆 周 运 动
06 平 抛 圆 周 运 动
Part One
轨迹是圆或圆的一部分
是一种特殊的曲线运动
公式
角速度公式：ω=θ/t，其中θ为转过的角度，t为时间 线速度公式：v=s/t，其中s为弧长，t为时间 向心加速度公式：a=v²/r，其中v为线速度，r为半径 周期公式：T=2πr/v，其中T为周期，r为半径，v为线速度
Part Two
变速圆周运动
定义
运动轨迹为抛物线
水平方向做匀速直 线运动
竖直方向做自由落 体运动
公式
平抛圆周运动的线速度公式： v=ωr
平抛圆周运动的角速度公式： ω=√(g/r)
平抛圆周运动的向心加速度 公式：a=ω^2r
平抛圆周运动的周期公式： T=2π√(r/g)
THANKS
汇报人：XX
添加标题
添加标题
添加标题
添加标题
运动方向：竖直上抛圆周运动方向 不断变化
运动周期：竖直上抛圆周运动周期 为定值
公式
竖直上抛圆周运动的速度公式：v = ωr
竖直上抛圆周运动的角速度公式：ω = v/r
竖直上抛圆周运动的周期公式：T = 2πr/v
竖直上抛圆周运动的向心加速度公式：a = v²/r
变速圆周运动是指物体在圆周运动过程中速度大小或方向发生变化的运动。
变速圆周运动中，物体受到的向心力和离心力也会发生变化，与匀速圆周运动不同。

圆周运动中的临界问题一.两种模型:(1)轻绳模型：一轻绳系一小球在竖直平面内做圆周运动.小球能到达最高点(刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力）. 类此模型：竖直平面内的内轨道(2)轻杆模型：一轻杆系一小球在竖直平面内做圆周运动，小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 . （杆既可以提供拉力，也可提供支持力或侧向力.） ①当v ＝0 时，杆对小球的支持力 小球的重力； ②当0<v <gr 时，杆对小球的支持力于小球的重力；③当v＝gr 时，杆对小球的支持力 于零； ④当v >gr 时，杆对小球提供 力. 类此模型：竖直平面内的管轨道.1、圆周运动中绳模型的应用 【例题1】长L ＝0.5m 的细绳拴着小水桶绕固定轴在竖直平面内转动，筒中有质量m ＝0.5Kg 的水，问：（1）在最高点时，水不流出的最小速度是多少？（2）在最高点时，若速度v ＝3m/s ，水对筒底的压力多大？【训练1】游乐园里过山车原理的示意图如图所示。

设过山车的总质量为m ，由静止从高为h 的斜轨顶端A 点开始下滑，到半径为r 的圆形轨道最高点B 时恰好对轨道无压力。

求在圆形轨道最高点B 时的速度大小。

【训练2】．杂技演员在做水流星表演时，用绳系着装有水的水桶，在竖直平面内做圆周运动，若水的质量m ＝0．5 kg ，绳长l=60cm ，求：(1)最高点水不流出的最小速率。

(2)水在最高点速率v ＝3 m ／s 时，水对桶底的压力．2、圆周运动中的杆模型的应用【例题2】一根长l ＝0.625 m 的细杆，一端拴一质量m=0.4 kg 的小球，使其在竖直平面内绕绳的另一端做圆周运动，求：(1)小球通过最高点时的最小速度；(2)若小球以速度v 1=3.0m ／s 通过圆周最高点时，杆对小球的作用力拉力多大?方向如何？vR 【训练3】如图所示，长为L 的轻杆一端有一个质量为m 的小球，另一端有光滑的固定轴O ，现给球一初速度，使球和杆一起绕O 轴在竖直平面内转动，不计空气阻力，则（ ） A.小球到达最高点的速度必须大于gLB .小球到达最高点的速度可能为0 C.小球到达最高点受杆的作用力一定为拉力 D.小球到达最高点受杆的作用力一定为支持力【训练4】如图所示，在竖直平面内有一内径为d 的光滑圆管弯曲而成的环形轨道，环形轨道半径R 远远大于d ，有一质量为m 的小球，直径略小于d ，可在圆管中做圆周运动。

2024版新课标高中物理模型与方法水平面内的圆周运动模型目录【模型一】圆锥摆、圆锥斗、圆碗模型【模型二】火车转弯模型【模型三】水平路面转弯模型【模型四】圆盘模型【模型一】圆锥摆、圆锥斗、圆碗模型一．圆锥摆模型1.结构特点：一根质量和伸长可以不计的轻细线，上端固定，下端系一个可以视为质点的摆球在水平面内做匀速圆周运动，细绳所掠过的路径为圆锥表面。

2.受力特点：摆球质量为m，只受两个力即竖直向下的重力mg和沿摆线方向的拉力F T。

两个力的合力，就是摆球做圆周运动的向心力F n，如图所示(也可以理解为拉力F T的竖直分力与摆球的重力平衡，F T的水平分力提供向心力)。

3.运动特点：摆长为l，摆线与竖直方向的夹角为θ的圆锥摆，摆球做圆周运动的圆心是O，圆周运动的轨道半径是r=l sinθ=mg tanθ=ma n=mω2l sinθ=mv2/(l sinθ)向心力F合摆线的拉力F T=mg/cosθ【讨论】：(1)当摆长一定，摆球在同一地点、不同高度的水平面内分别做匀速圆周运动时，据cosθ=g/(ω2l)可知，若角速度ω越大，则θ越大，摆线拉力F T=mg/cosθ也越大，向心加速度a n=g tanθ也越大，线速度v=ωr =gl sinθtanθ也越大。

结论是：同一圆锥摆，在同一地点，若θ越大，则摆线的拉力越大，向心力越大，向心加速度也越大，转动的越快，运动的也越快，。

(2)当l cosθ为定值时(l cosθ=h为摆球的轨道面到悬点的距离h，即圆锥摆的高度)，摆球的质量相等、摆长不等的圆锥摆若在同一水平面内做匀速圆周运动，则摆线拉力F T=mg/cosθ，向心力F合=mg tanθ，向心加速度a n=g tanθ，角速度ω=g/h，线速度v=ωr=gh tanθ。

结论是：在同一地点，摆球的质量相等、摆长不等但高度相同的圆锥摆，转动的快慢相等，但θ角大的圆锥摆，摆线的拉力大，向心力大，向心加速度大，运动得快。